排序算法之【快速排序】
📙作者简介: 清水加冰,目前大二在读,正在学习C/C++、Python、操作系统、数据库等。
📘相关专栏:C语言初阶、C语言进阶、C语言刷题训练营、数据结构刷题训练营、有感兴趣的可以看一看。
欢迎点赞 👍 收藏 ⭐留言 📝 如有错误还望各路大佬指正!
✨每一次努力都是一种收获,每一次坚持都是一种成长✨

目录
前言
1. 快速排序
1.1 hoare版本
1.2 挖坑法
1.3 双指针版本
2. 非递归实现快速排序
总结
前言
快速排序是一种常用的排序算法,也是一种很高效的排序的,它是由Hoare于1962年提出的一种二叉树结构的交换排序方法。本篇文章我将带你深入了解快速排序。
1. 快速排序
快速排序是一种常用的排序算法,它的基本思想是通过一趟排序将待排序的数据分割成独立的两部分,其中一部分的所有数据都比另一部分的所有数据小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列的目的。快速排序常见的实现方法主要分为三种版本:
- hoare版本
- 挖坑法版本
- 前后指针版本
我们废话不多说直接步入正题。
1.1 hoare版本
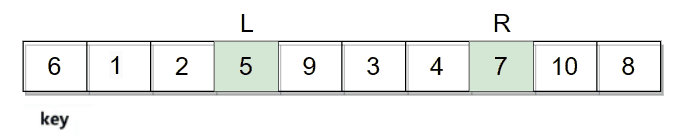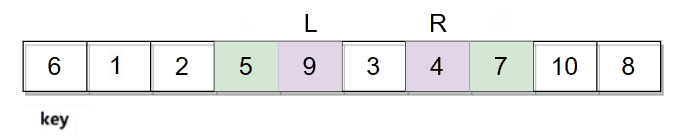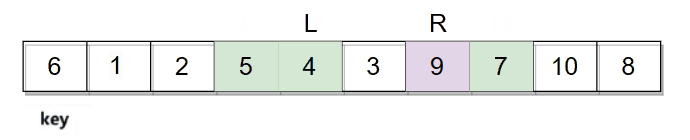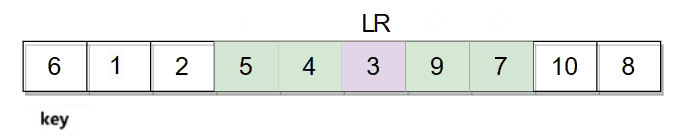
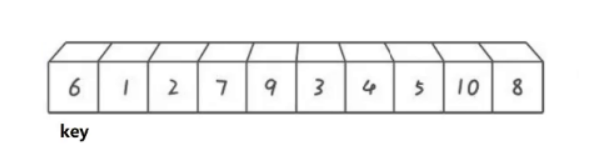
hoare版本是选择一个key值(一般选用最左边)例如:

然后开始从数组两边开始移动寻找符合条件的值,R向左移动寻找小于key的值,L向右移动寻找大于key的值。R和L都找到符合条件的数字后进行交换。

然后再继续走,直到L和R相遇停止。
它们相遇的位置是数字3,3比key小,最后再将相遇位置的数据和key的数据进行交换。整个逻辑过程如下图:
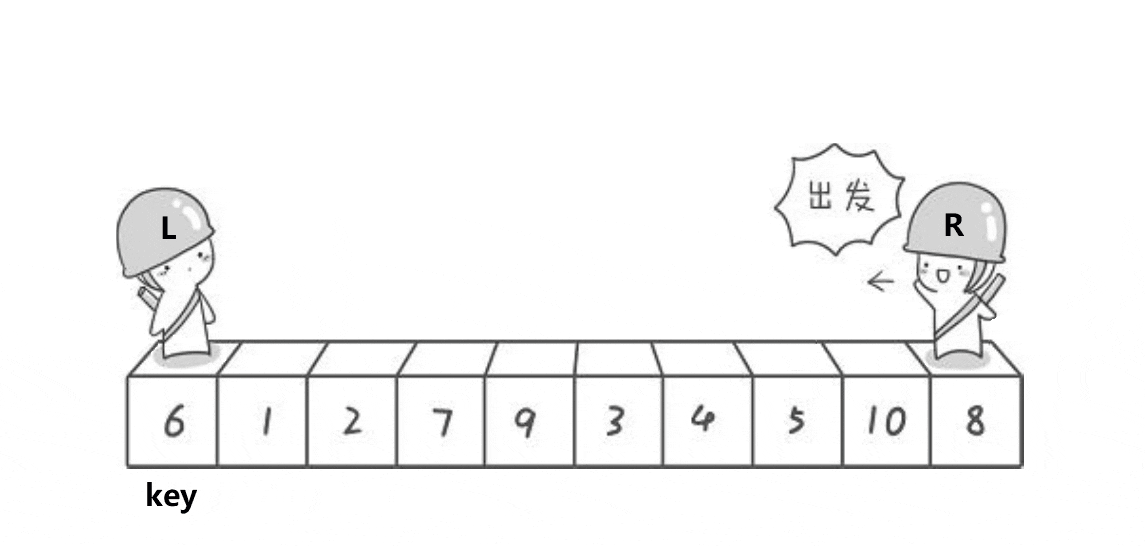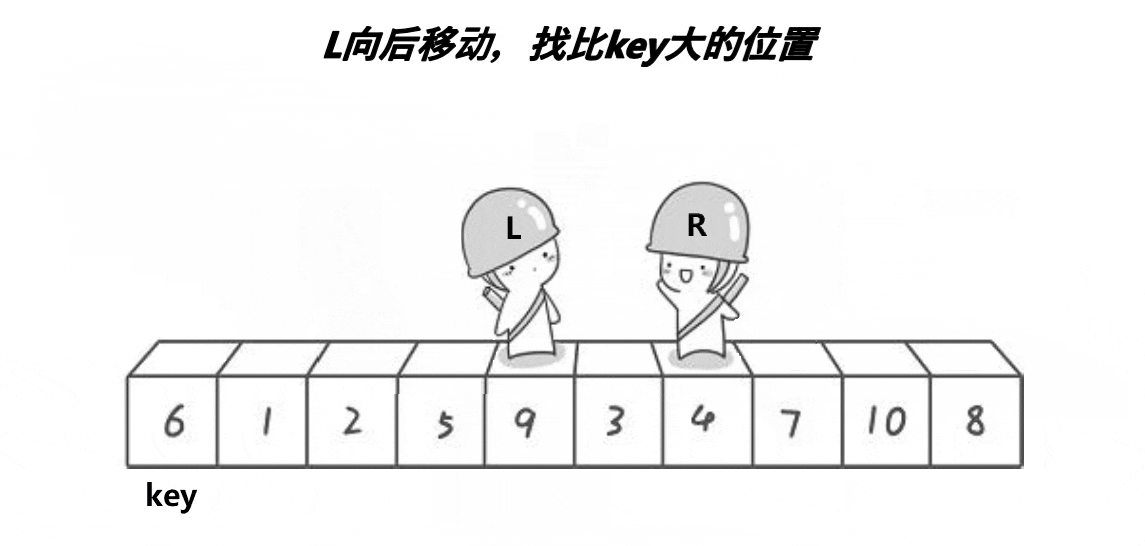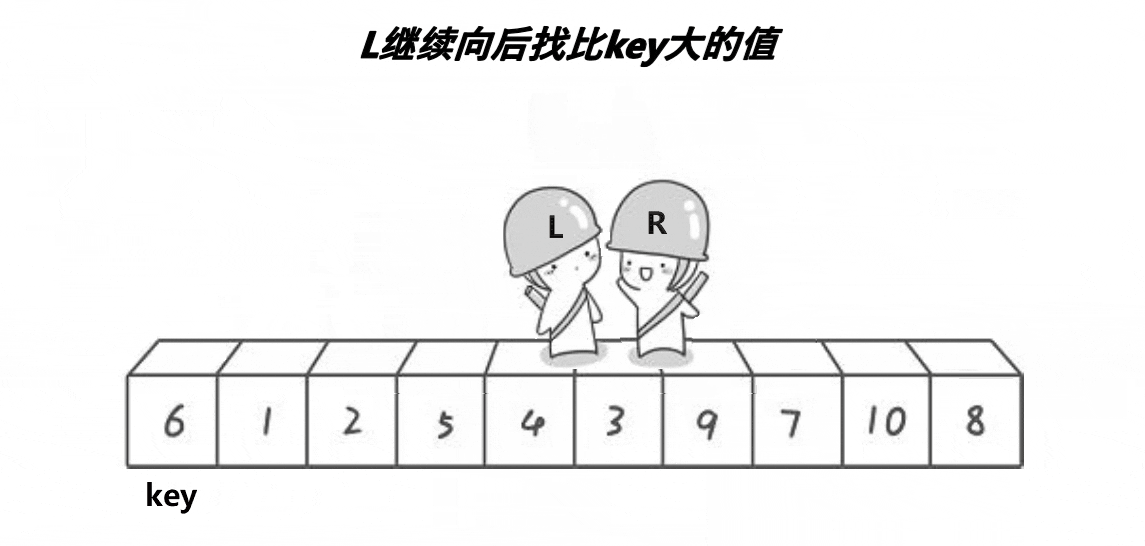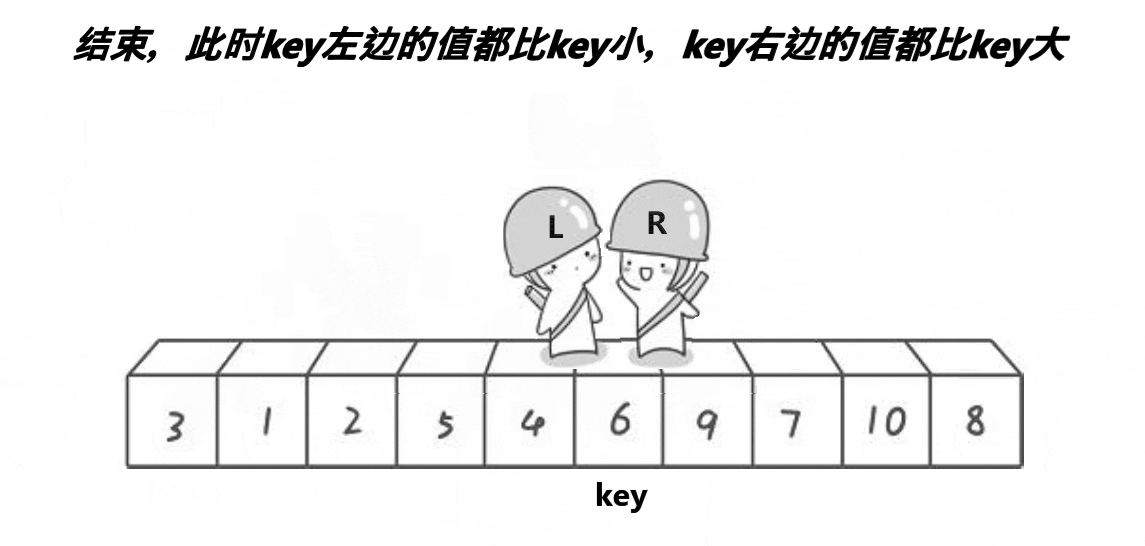
这个图呈现的逻辑过程更加形象,然后我们再从R和L相遇的位置将数组分为两部分,当左半部分和右半部分有序,那么这个数组就会有序,所以我们重复上述过程:

继续分,数组最终被细分为一个数据或没有数据。
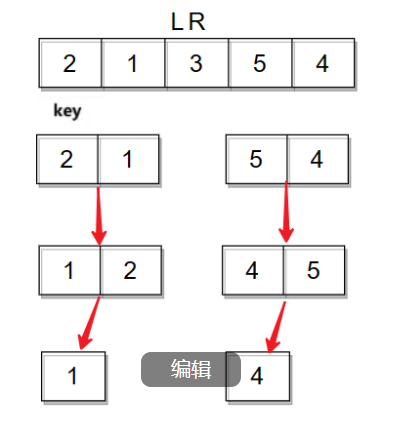
当数据为1个或没有时就开始返回,执行完毕后左半部分就变得有序,右半部分也是这样的逻辑,返回后两边子数组就会变得有序,进而使整个数组有序。以上便是hoare版本的整个过程。
接下来我们对代码进行实现:
void PathSort(int* a, int left,int right)
{int key = a[left];while (left < right){while (a[right] > a[key]){right--;}while (a[left] < a[key]){left--;}Swap(&a[left], &a[right]);}Swap(&key, &a[right]);
}快速排序的hoare版本有很多的坑,上述的代码是否存在错误呢?
上述的代码存3个问题:
- 死循环问题
- 数组越界问题
- key值交换问题
首先是死循环问题,R要找比key小的数据,L要找比key大的数据,那当L和R都遇到了和key相同的数据时,它们都停止移动,开始进行交换,交换后仍然相等,以此往复一直交换,进而形成了死循环。
数组越界问题,R找比key的值,如果R一直到数组遍历结束都没有找到,那它就会发生越界。
key值交换问题,我们在上述逻辑中,需要将key值(第一个数据)位置上的数据与L和R相遇位置的数据进行交换。而上述代码中交换的是key的值与L和R相遇位置的数据,实际上第一个数据(key值位置)并没有变,这样会造成数据丢失。
这三个问题都是在编写代码时经常遇到的错误。改正后代码如下:
int PathSort(int* a, int left,int right)
{int key = left;while (left < right){while (right>left && a[right] >= a[key]){right--;}while (right > left && a[left] <= a[key]){left++;}Swap(&a[left], &a[right]);}Swap(&a[key], &a[left]);return left;
}
上述代码我们是进行了一次调整,接下来就是递归使得左右两边数组有序。递归调用这里没有什么问题,重点在于递归结束条件。当递归到最后时,要么是数组只有一个数据,要么是没有数据。
那要如何编写设置结束条件呢?
以左边递归为例:第一次进入左边区间是0到4,第二次是0到1,然后key是下标为1的数据,key-1=0,第三次调用传入的key-1=begin=0,返回后调用右边,右边没有数据,key+1=2,end=1,所以由此我们可以做出判断,当begin>=end时,就证明递归已经到最小,然后就返回。
递归过程如下图:

void QuickSort(int* a, int begin,int end)
{if (begin >= end){return;}int key=PathSort(a, begin, end);QuickSort(a, begin, key - 1);QuickSort(a, key + 1, end);
}从上述的逻辑过程,可以发现L和R相遇的位置一定比key小(相遇位置比key小交换才有意义),那凭什么说L和R相遇位置一定比key小?
它是有一个前提的,就是一定要让R先走,但是又会存在两种情况:
- 最后一次R不动让L去相遇。
- L不动让R去相遇。
如下图让R先走,最后是R不动让L去相遇,但如果是L先走,当R到下标为6的位置停止交换后,L开始走,此时相遇位置就会变成下标为6的位置,数据是9比6大。(R不动,让L去相遇)
当然还有一种情况,最后一次时是L不动让R去相遇:

两次交换后如上图,此时R先走,11比key大R会继续走,R就会去和L相遇,相遇的位置还是比key小(L和R交换后,L位置数据一定比key小)。
上述的方式和代码排序很不稳,上述过程最理想的状态是key的值是中位数,这样在分割数组进行递归时能尽可能将数组二分。
最坏的情况就是没有比key小的数据或者大的数据,那么就会造成如下情况:
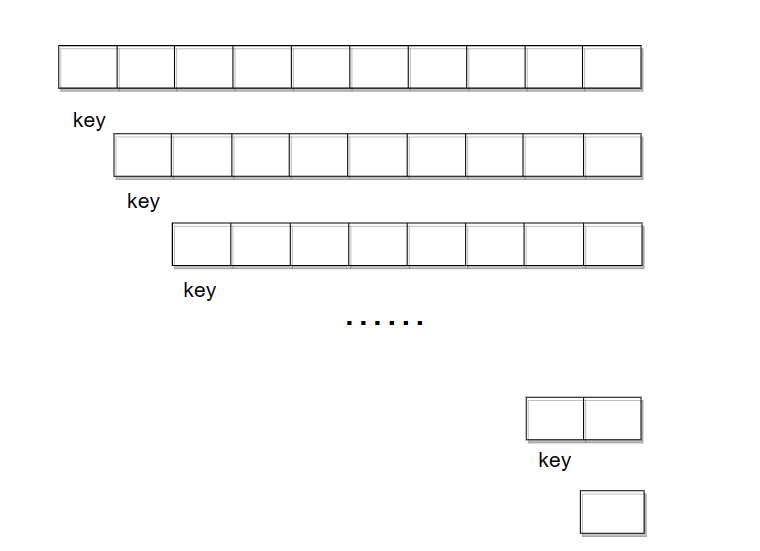
这样它的时间复杂度和空间复杂度也会变差,所以我们还需要对hoare版本的进行优化,以避免这样情况的发生。我们可以将左右和中间的值进行比较,取三数的中间值作为key值。优化后:
//三数取中
int GetMid(int* a, int left, int right)
{int mid = (left + right) / 2;if (a[mid] > a[left]){if (a[mid] < a[right]){return mid;} else if(a[left]>a[right]){return left;}else{return right;}}else//a[left]>a[mid]{if (a[mid] > a[right]){return mid;}else if (a[right] < a[left]){return right;}else{return left;}}
}
int PathSort(int* a, int left,int right)
{int mid = GetMid(a, left, right);Swap(&a[left], &a[mid]);int key = left;while (left < right){while (right>left && a[right] >= a[key]){right--;}while (right > left && a[left] <= a[key]){left++;}Swap(&a[left], &a[right]);}Swap(&a[key], &a[left]);return left;
}1.2 挖坑法
挖坑法是对hoare版本思路上的一种优化,挖坑法的整体逻辑如下:
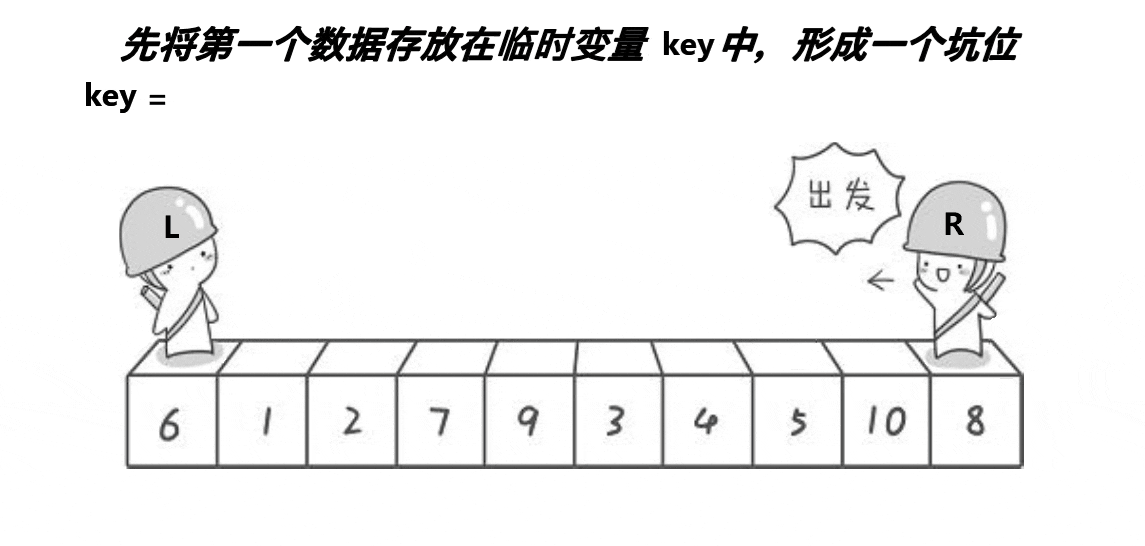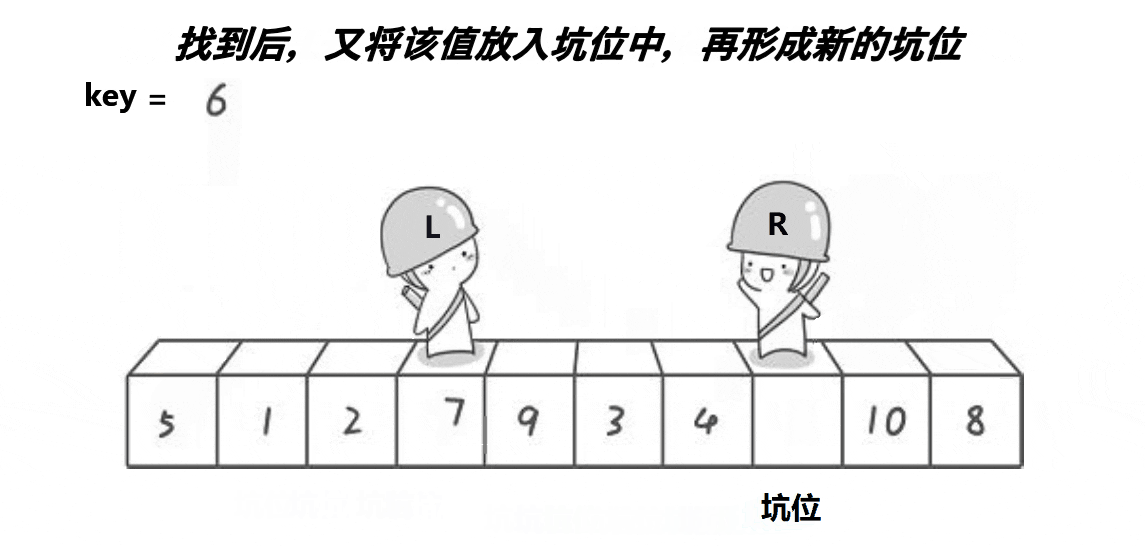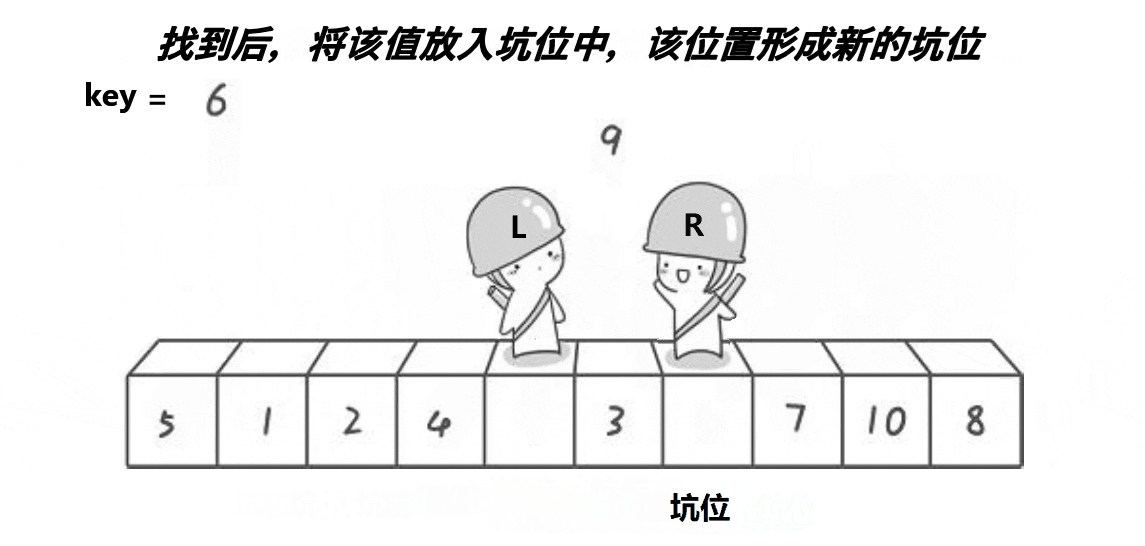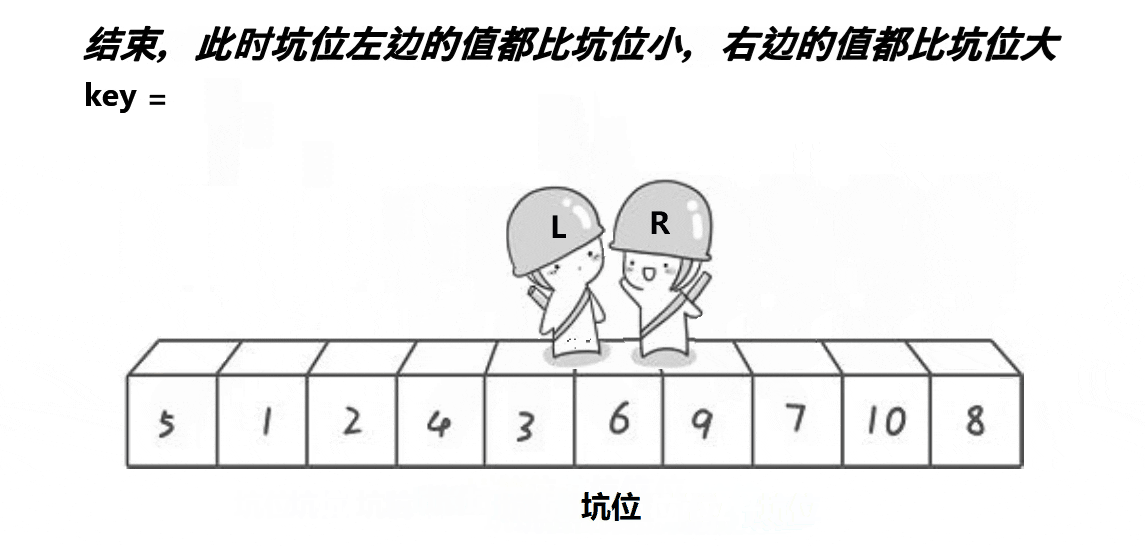
挖坑法不用考虑R先走还是L先走,开始时第一个数据作为坑位,必须R先走,R找到比key小的数数据填补到坑位,R位置形成新的坑位。然后L开始走,遇到比key大的将数据填补到坑位,然后L位置形成新的坑位。具体代码如下:
int PathSort2(int* a, int left, int right)
{int mid = GetMid(a, left, right);Swap(&a[left], &a[mid]);int key = a[left];//保存key值左边形成第一个坑位int hole = left;while (left < right) {//右边先走,寻找比key小的数据,填补到左边坑位while (right > left && a[right] >=key){right--;}a[hole] = a[right];hole = right;//左边走,寻找比key大的数据,填补到右边坑位while (right > left && a[left] <= key){left++;}a[hole] = a[left];hole = left;}a[hole] =key;return hole;}1.3 双指针版本
双指针法是对快排的更近一步优化,相对于前两种,思路和代码也更简单,使用两个指针cur和prev,来控制数据进行调整。
逻辑如下:
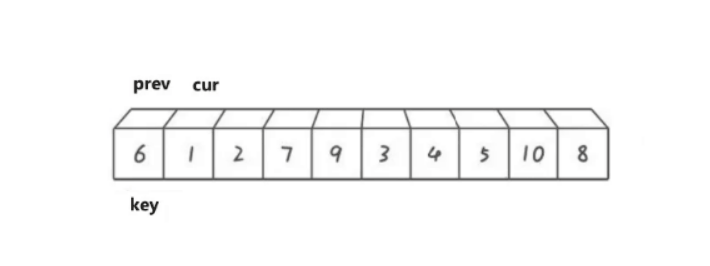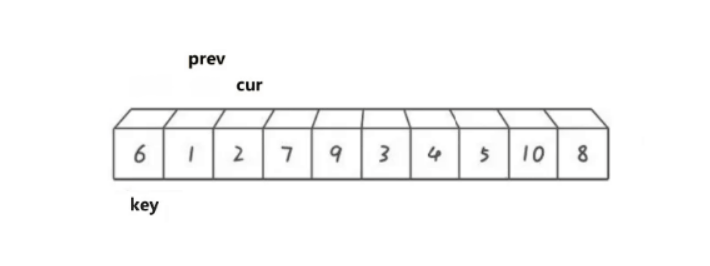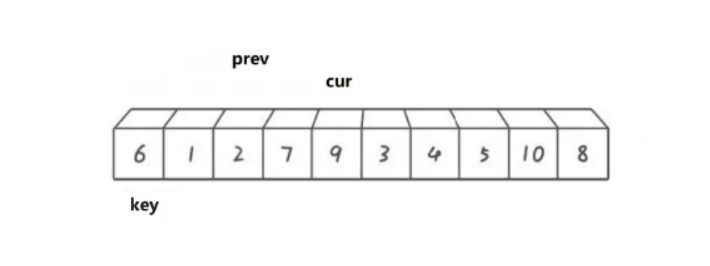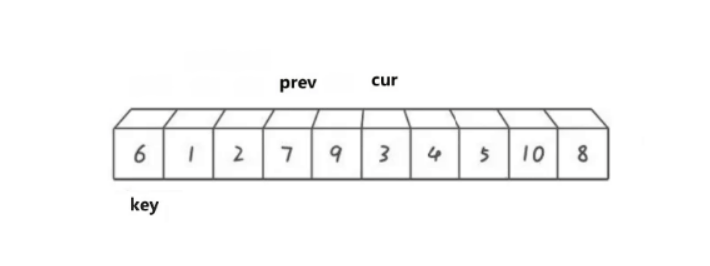
cur遍历数组,如果cur比key小,那就prev向后移动,将prev指向的数据于cur指向的数据进行交换。
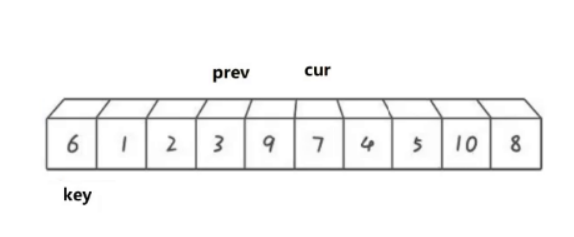
然后cur继续向后走,遇到比key小的数据就重复上述过程:
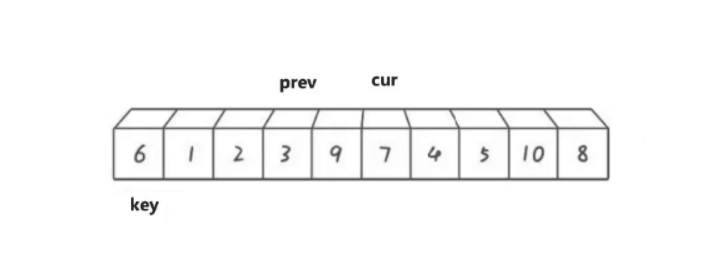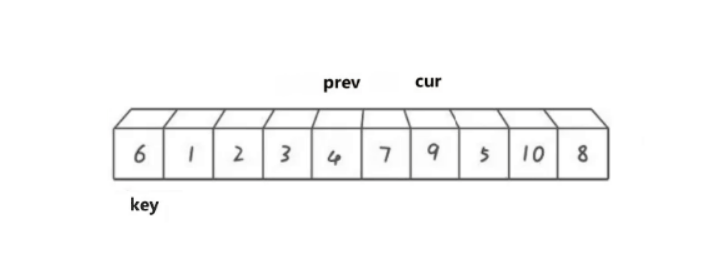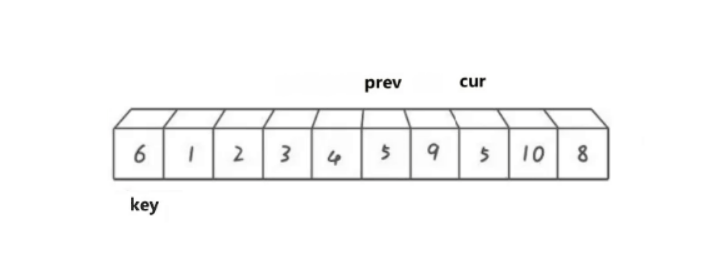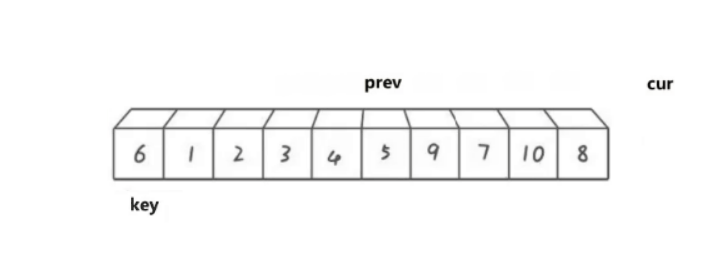
直到cur遍历结束停止,之后再将prev最终指向位置的数据与key位置的数据进行交换。最终情况如下图:
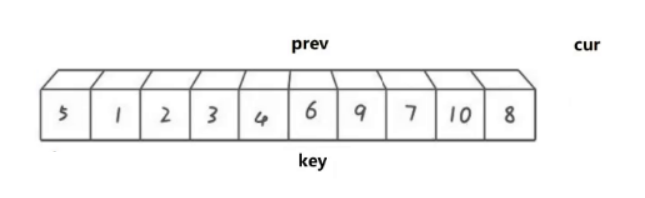
根据上述的逻辑,我们对代码进行实现:
int PathSort3(int* a, int left, int right)
{int cur = left + 1;int prev = left;int key = left;while (cur <= right){if (a[cur] <a[key] ){prev++;Swap(&a[prev], &a[cur]);}cur++;}Swap(&a[key], &a[prev]);return prev;}在cur指向1和2时,cur指向的数据依然和prev指向的数据进行了交换(此时cur和prev指向同一个数据),此时交换并没有什么意义,所以我们也可以为了防止prev和cur指向同一位置时进行交换,这里我们可以进行优化:
int PathSort3(int* a, int left, int right)
{int mid = GetMid(a, left, right);Swap(&a[left], &a[mid]);int cur = left + 1;int prev = left;int key = left;while (cur <= right){if (a[cur] <a[key] && ++prev!=cur){Swap(&a[prev], &a[cur]);}cur++;}Swap(&a[key], &a[prev]);return prev;}双指针法不需要考虑从哪边先走,也不需要考虑数组越界问题,代码和逻辑都十分的清晰简单。在这三种方法的实际调用时都是使用了递归,来进行分治排序。
但快速排序使用递归是需要不断进行开空间的,快速排序的二分递归模式类似于满二叉树,我们知道,满二叉树的后两层的节点个数占了总个数的75%,所以我们可以考虑在递归到小区间时使用插入排序来进行优化。
void QuickSort2(int* a, int begin, int end)
{if (begin >= end){return;}if ((end - begin + 1) > 10){int key = PathSort3(a, begin, end);QuickSort(a, begin, key - 1);QuickSort(a, key + 1, end);}else{InsertSort(a + begin, end - begin + 1);}}
同时我们还可以使用非递归的方法来实现快排。
2. 非递归实现快速排序
上述的快速排序使用了递归,但使用递归还是存在弊端的,递归的深度问题,递归创建的空间在栈区,而栈区的空间大概只有8MB,所以我们还是很有必要学习非递归的方法。
非递归实现快排需要用到栈的数据结构,通过栈来模拟系统栈区。
不断地入栈每次调整的数组区间,使用栈的特性来模拟递归调用的调整函数。
还是以上述的数组为例:
以左边为例:

先入栈0和9(数据的区间下标),然后出栈,取栈顶元素作为调整函数的参数,然后调用调整函数,再将key两边的数组下标区间入栈,直至栈为空结束。具体代码实现如下:
逻辑比较简单,不再进行细节讲解。
void QuickSort3(int* a, int begin, int end)
{Stack st;InItStack(&st);StackPush(&st, end);StackPush(&st, begin);while (!IsEmpty(&st)){int left=TopData(&st);StackPop(&st);int right = TopData(&st);StackPop(&st);int key =PathSort3(a, left, right);if (key < right){StackPush(&st, right);StackPush(&st, key+1);}if (left < key - 1){StackPush(&st, key - 1);StackPush(&st, left);}}DestoryStack(&st);}总结
快速排序是一种极其高效的排序方法,从上述的分析快速排序使用的二分分治排序的方法,可以得出时间复杂度为O(N*logN),同时快速排序并不稳定,我们使用了各种方法来进行优化,使它的时间复杂度稳定在O(N*logN)。好了以上便是本期全部内容,感谢阅读!
相关文章:

排序算法之【快速排序】
📙作者简介: 清水加冰,目前大二在读,正在学习C/C、Python、操作系统、数据库等。 📘相关专栏:C语言初阶、C语言进阶、C语言刷题训练营、数据结构刷题训练营、有感兴趣的可以看一看。 欢迎点赞 👍…...

声明式调用 —— SpringCloud OpenFeign
Feign 简介 Spring Cloud Feign 是一个 HTTP 请求调用的轻量级框架,可以以 Java 接口注解的方式调用 HTTP 请求,而不用通过封装 HTTP 请求报文的方式直接调用 Feign 通过处理注解,将请求模板化,当实际调用的时候传入参数&#x…...
-- fota - 底层固件升级)
LuatOS-SOC接口文档(air780E)-- fota - 底层固件升级
fota.init(storge_location, len, param1)# 初始化fota流程 参数 传入值类型 解释 int/string fota数据存储的起始位置 如果是int,则是由芯片平台具体判断 如果是string,则存储在文件系统中 如果为nil,则由底层决定存储位置 int 数据存…...

第二章 Introduction
Armv8.4 架构引入了在安全状态下的虚拟化扩展。Arm SMMU v3.2 架构 [1] 增加了对安全流的第二阶段翻译的支持,以补充 Armv8.4 PE 中的安全 EL2 翻译体制。这些架构特性使得可以在安全状态下将彼此不信任的软件组件隔离开来。隔离是实现最小权限原则的机制࿱…...

WebGL 渲染三维图形作为纹理贴到另一个三维物体表面
目录 渲染到纹理 帧缓冲区对象和渲染缓冲区对象 帧缓冲区对象 帧缓冲区对象的结构 如何实现渲染到纹理 示例程序(FramebufferObject.js) 创建帧缓冲区对象(gl.createFramebuffer()) gl.createFra…...

国庆《乡村振兴战略下传统村落文化旅游设计》许少辉八一新书行将售罄
国庆《乡村振兴战略下传统村落文化旅游设计》许少辉八一新书行将售罄 国庆《乡村振兴战略下传统村落文化旅游设计》许少辉八一新书行将售罄...
Source Insight 工具栏图标功能介绍
这篇文章并不介绍 Source Insight 的具体使用方法,这类教程网上有很多,这里只分析 Souce Insight 工具栏图标的功能。 文章目录 Source Insight 简介Souce Insight 工具栏文件操作新建(CtrlN)打开(CtrlO)保…...

模板与泛型编程-函数模板
本专栏由于缺少函数模板专题,我本以为这个不用讲解,但由于某些同学基础比较薄弱,特地在此补充一下。 函数模板的定义一般都在头文件中。 一、如何定义一个模板函数 下面是一个求和函数 template<typename T,typename U> auto Add(T a, U b) {return a + b; }int...

了解ActiveMQ、RabbitMQ、RocketMQ和Kafka的特点
ActiveMQ ActiveMQ是一种基于JMS(Java消息服务)规范的消息中间件,由Apache基金会开发和维护 核心组件和特点: Broker(代理):ActiveMQ的核心组件是Broker,它负责接收、存储和路由消息…...
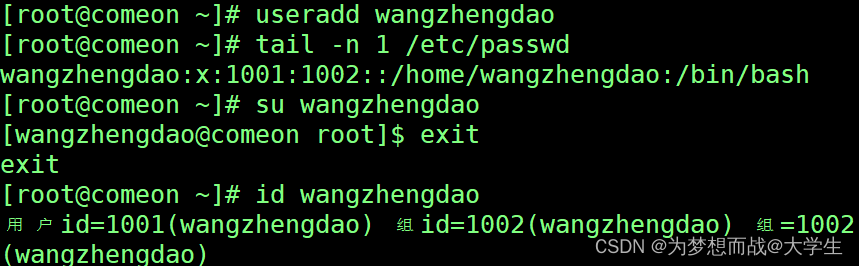
第七章 用户和组管理
7.1 Linux中的用户和组的分类 用户类别 超级用户(0) root 系统用户(1-999) 一般用户(1000-60000) 组类别 管理组 root 基本组(默认组/主组) 附加组(额外组) 7.2 用户管理 7.2.1 添加新用户 语法 useradd 【…...

给奶牛做直播之三
一、前言 上一篇给牛奶做直播之二 主要讲用RTMP搭建点播服务器,整了半天直播还没上场,今天不讲太多理论的玩意,奶牛今天放假了也不出场,就由本人亲自上场来个直播首秀,见下图,如果有兴趣的话࿰…...

【Java 进阶篇】MySQL 数据控制语言(DCL):管理用户权限
MySQL 是一个强大的关系型数据库管理系统,提供了丰富的功能和选项来管理数据库和用户。数据库管理员(DBA)通常使用数据控制语言(Data Control Language,简称 DCL)来管理用户的权限和访问。 本文将详细介绍…...

WPF 03
staticResource和dynamicResource的区别 首先看一个案例 MainWindow.xaml <Window x:Class"WpfDay03.MainWindow"xmlns"http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmlns:x"http://schemas.microsoft.com/winfx/2006/xaml&quo…...
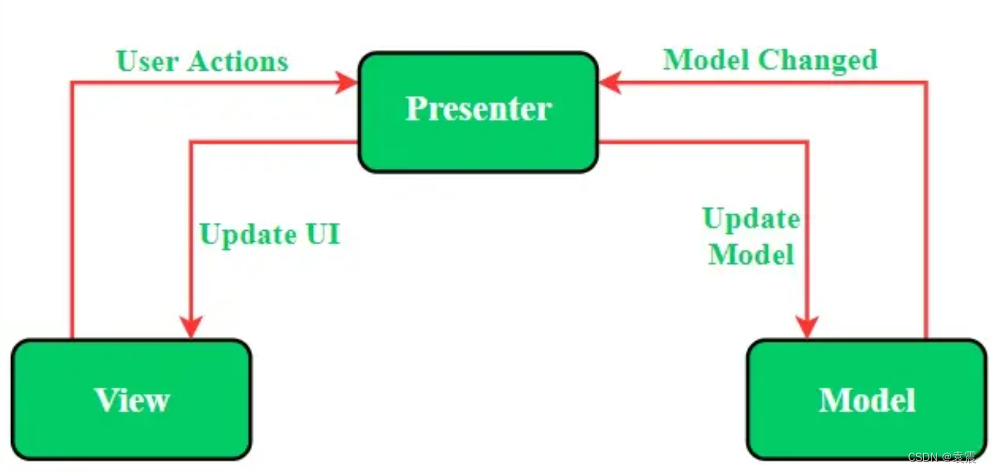
Android 使用kotlin+注解+反射+泛型实现MVP架构
一,MVP模式的定义 ①Model:用于存储数据。它负责处理领域逻辑以及与数据库或网络层的通信。 ②View:UI层,提供数据可视化界面,并跟踪用户的操作,以便通知presenter。 ③Presenter:从Model层获…...

数据结构——堆(C语言)
本篇会解决一下几个问题: 1.堆是什么? 2.如何形成一个堆? 3.堆的应用场景 堆是什么? 堆总是一颗完全二叉树堆的某个节点总是不大于或不小于父亲节点 如图,在小堆中,父亲节点总是小于孩子节点的。 如图&a…...

B058-SpringBoot
目录 springboot概念与作用入门案例springboot运行方式热部署配置文件Profile多环境支持整合测试-springboot-testSpringboot-web1.返回json数据2.返回页面(模板技术)thymeleaf1.导入thymeleaf依赖2.模板文件3.controller4.启动类 SSM整合1.导包2.项目目…...
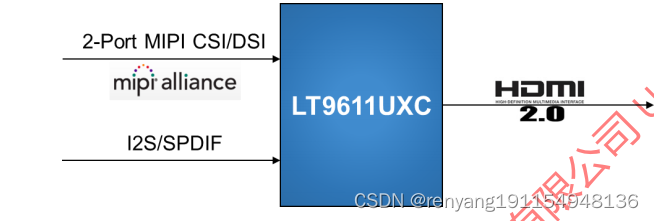
龙迅LT9611UXC 2PORT MIPICSI/DSI转HDMI(2.0)转换器+音频,内置MCU
龙迅LT9611UXC 1.描述: LT9611UXC是一个高性能的MIPI DSI/CSI到HDMI2.0转换器。MIPI DSI/CSI输入具有可配置的单 端口或双端口,1高速时钟通道和1~4高速数据通道,最大2Gbps/通道,可支持高达16Gbps的总带 宽。LT9611UXC支持突发…...
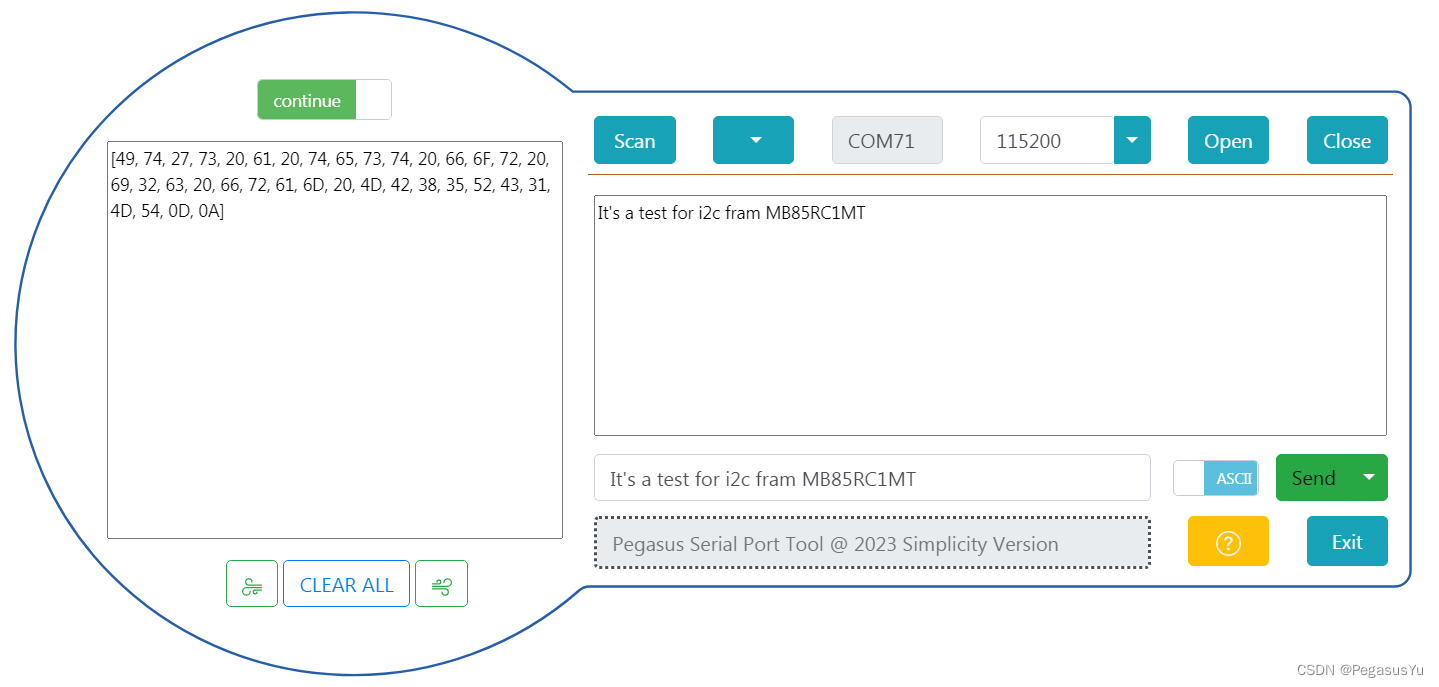
STM32存储左右互搏 I2C总线读写FRAM MB85RC1M
STM32存储左右互搏 I2C总线读写FRAM MB85RC1M 在较低容量存储领域,除了EEPROM的使用,还有铁电存储器FRAM的使用,相对于EEPROM, 同样是非易失性存储单元,FRAM支持更高的访问速度, 其主要优点为没有EEPROM持续写操作跨页…...
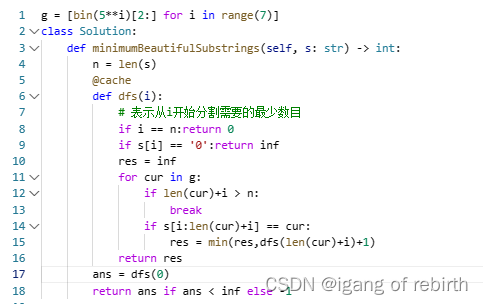
1340. 跳跃游戏 V;2039. 网络空闲的时刻;2767. 将字符串分割为最少的美丽子字符串
1340. 跳跃游戏 V 核心思想:动态规划记忆化搜索。定义dfs(i),表示从i开始最多可以访问多少个下标,然后统计往左跳和往右边跳的最大值,思路其实比较简单,但是代码我感觉还是不太好想。 2039. 网络空闲的时刻 核心思想…...
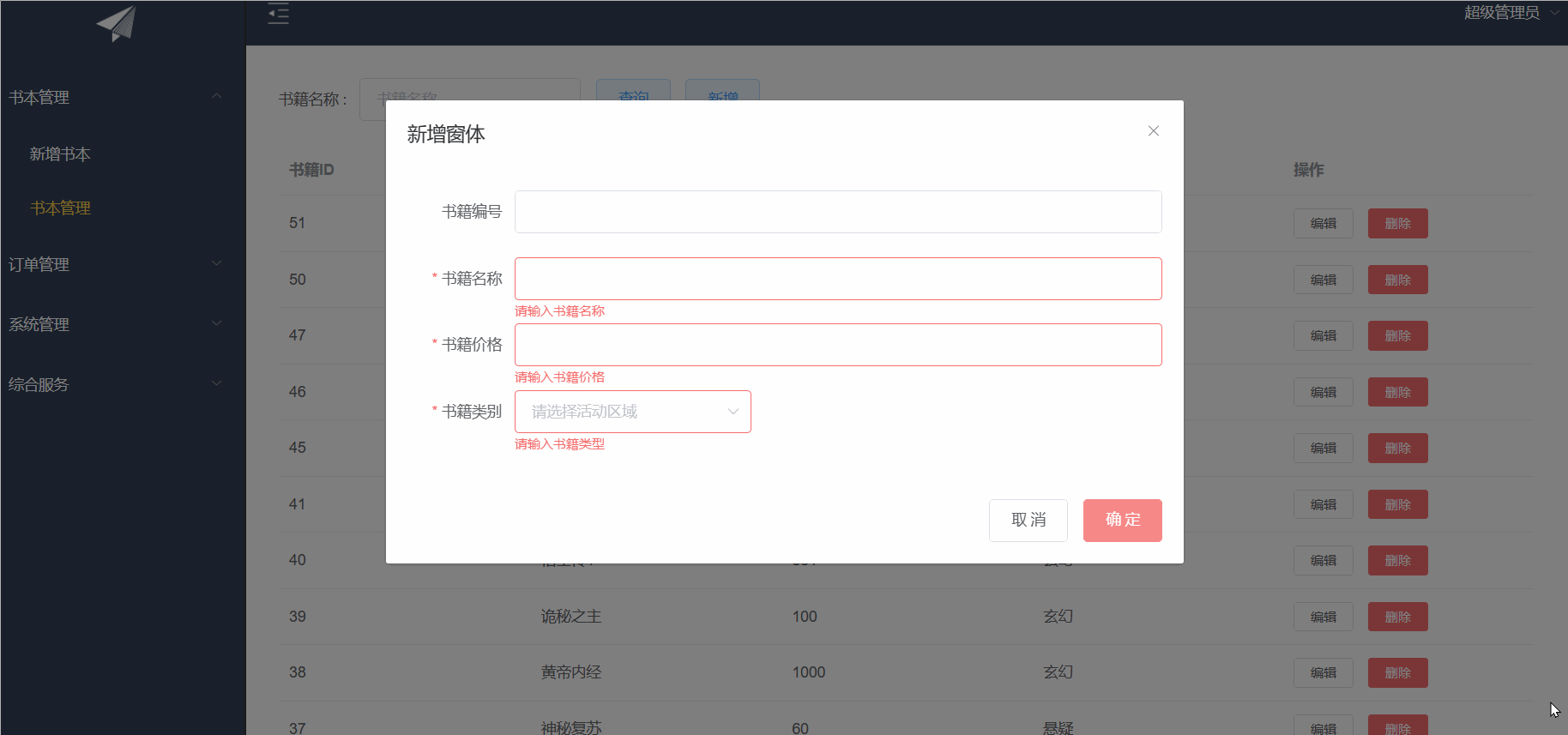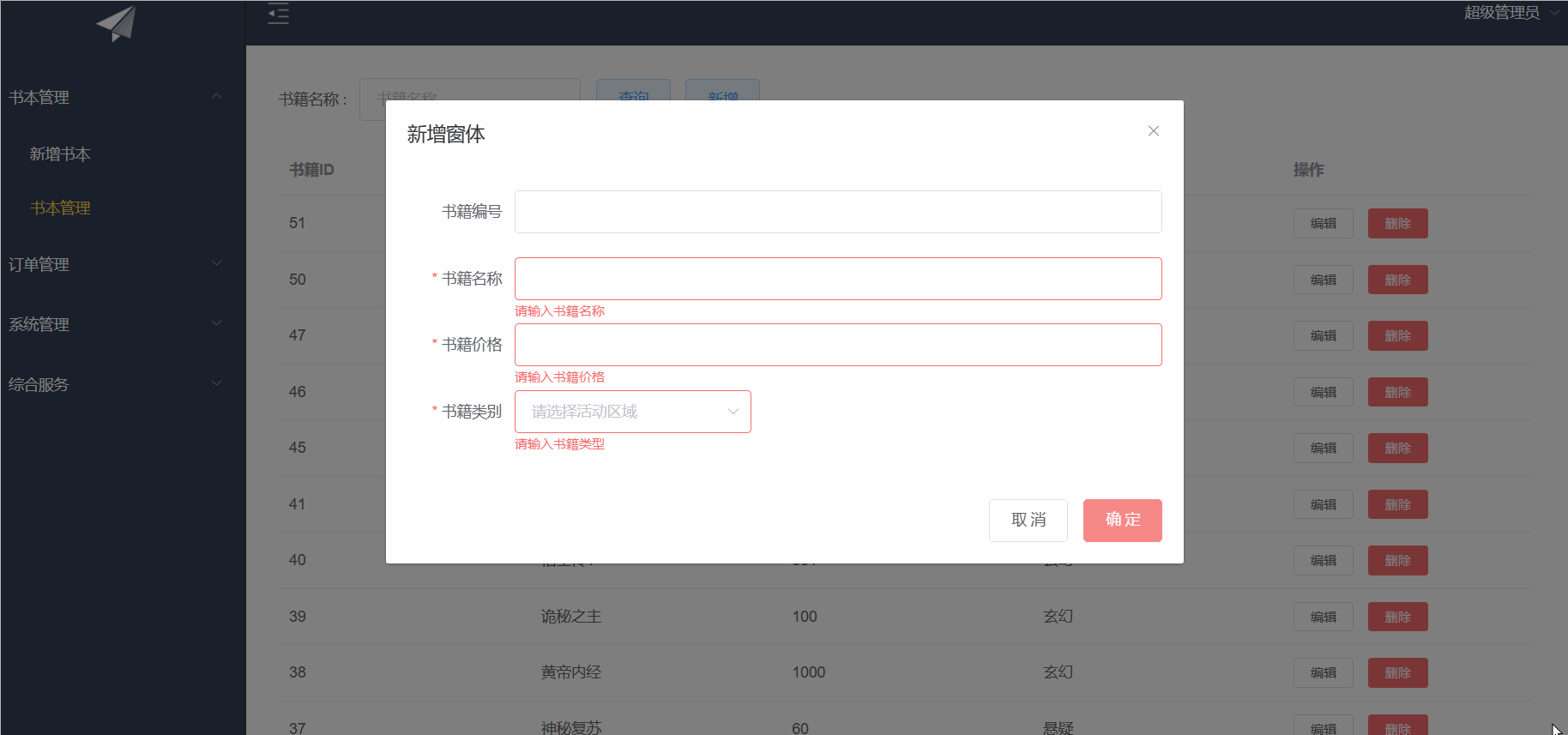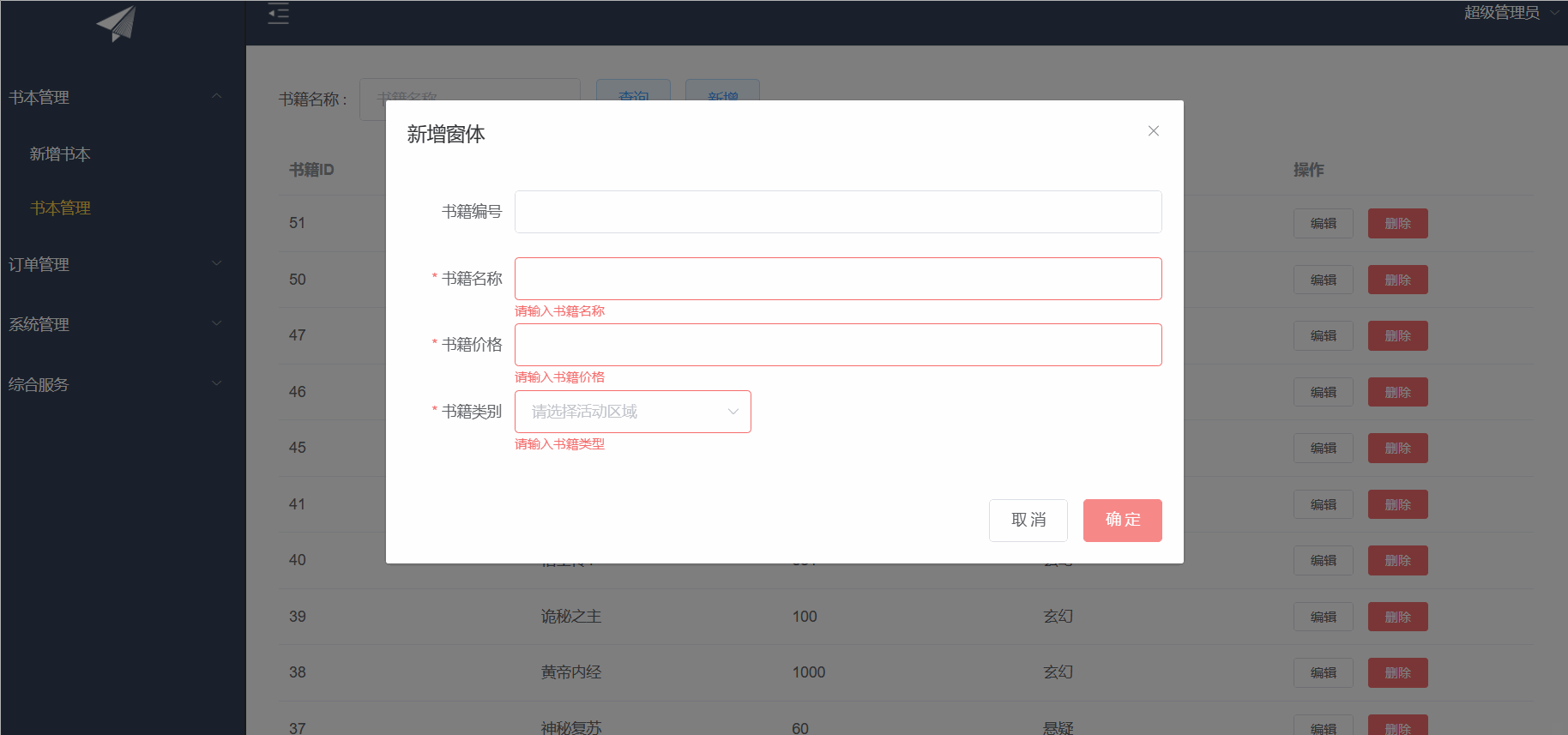
ElementUI之CUD+表单验证
目录 前言: 增删改查 表单验证 前言: 继上篇博客来写我们的增删改以及表单验证 增删改查 首先先定义接口 数据样式,我们可以去elementUI官网去copy我们喜欢的样式 <!-- 编辑窗体 --><el-dialog :title"title" :visib…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...
