数据结构——堆(C语言)
本篇会解决一下几个问题:
1.堆是什么?
2.如何形成一个堆?
3.堆的应用场景
堆是什么?
- 堆总是一颗完全二叉树
- 堆的某个节点总是不大于或不小于父亲节点
如图,在小堆中,父亲节点总是小于孩子节点的。
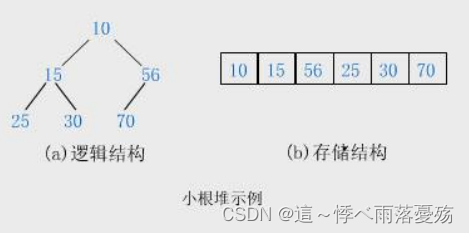
如图,在大堆中,父亲节点总是大于孩子节点的。

堆和二叉树还是有很大区别的,堆是用数组来实现的,尽管逻辑结构上是一颗二叉树,但在内存上要比二叉树好,普通的二叉树,你要用链表来存储他们的左右孩子,还要给他们分配空间,但堆只是用数组来表示。
如何形成一个堆?
堆的创建有向上调整和向下调整两种方式。
向上调整:从第一个非叶子节点开始向上调整,一直调整到根节点。
用int a[] ={1,5,3,8,7,6};来做例子,
如图所示,
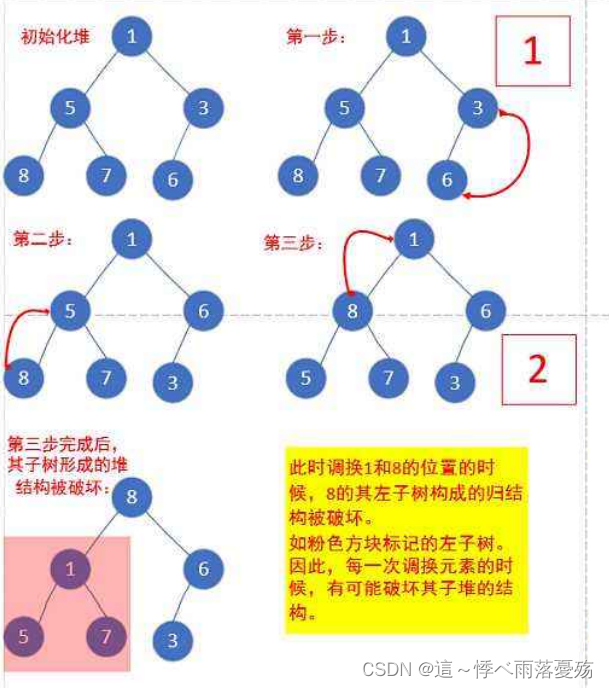
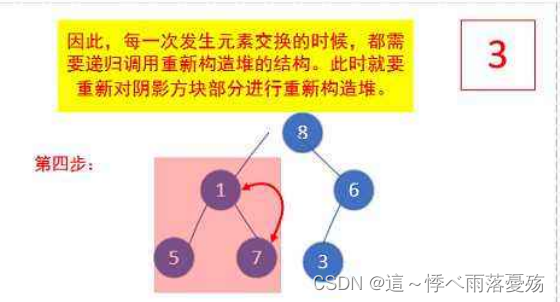
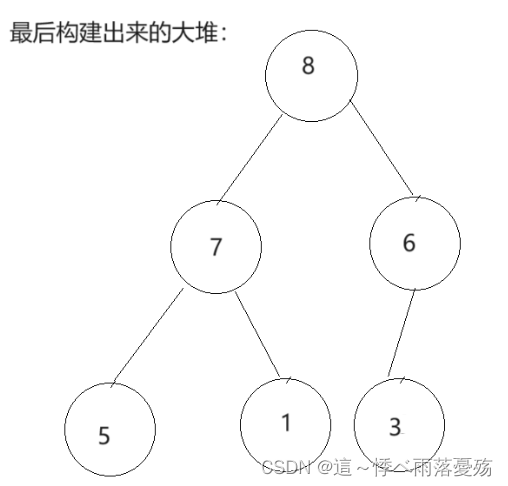
向下调整:从根节点开始,和左右孩子中小或者大的节点比较,交换,直到小于数组元素。
堆的插入
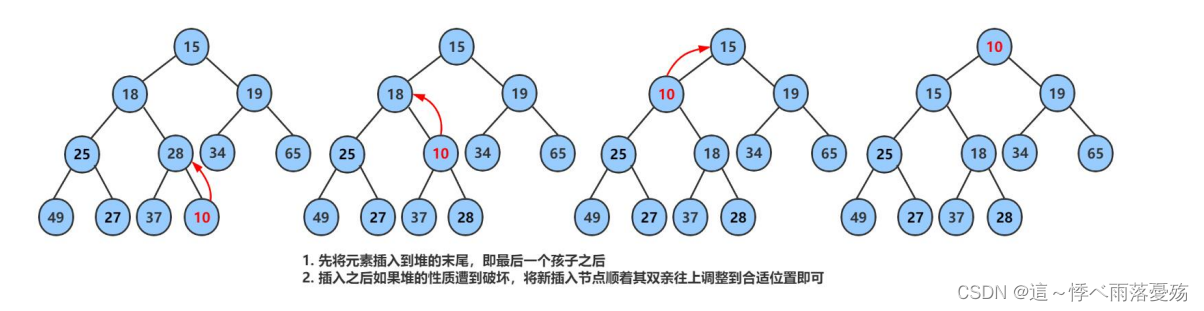
堆的删除
删除堆是删除堆顶的元素,将堆顶的元素根据最后一个数据一换,然后删除数组中最后一个元素,再进行向下调整算法。
这里想一想为什么要这样???
1.因为堆是有数组来创建的,如果直接删除堆顶的数据,第一个缺点就是会造成移动,从后往前覆盖,这样就会造成一个问题。兄弟节点变成父子节点,而且这样也不能很好的利用数组的优点。
2.如果是交换第一个和最后一个元素,这样有2个优点:
- 第一个是不会破坏除了堆顶的左右堆的结构。
- 第二个就是会利用数组的优点,数组读取速度很快,这样每次最后或最小的元素就放在了后面。
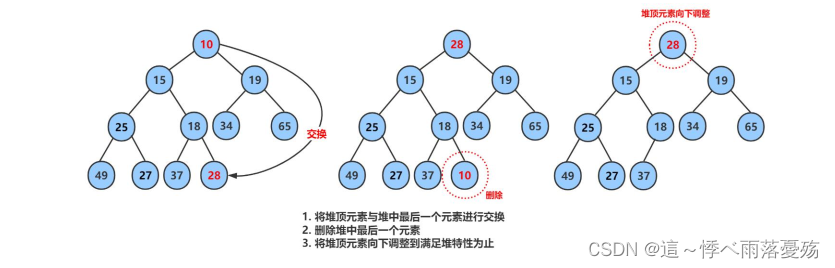
堆的时间复杂度
向下调整时间复杂度:
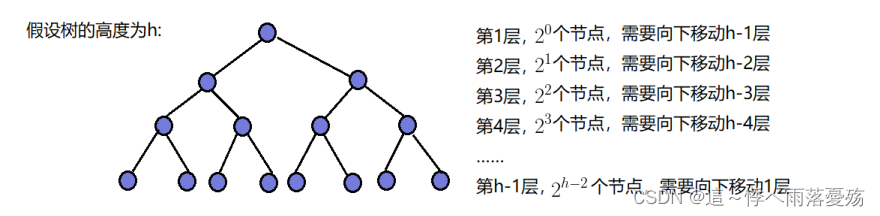 则要移动节点的总步数为:
则要移动节点的总步数为:

向上调整时间复杂度:

则要调整的节点总数为:

堆的应用场景
- 堆排序,可以用堆的建立和堆的删除来实现排序,堆排序十分稳定(相同元素的相对位置不会发生交换),而且时间复杂度都是O(N*logN)
- TOP-K问题,我们想一想王者荣耀中前100的玩家是怎么实现的,或者专业前10名...问题
1).先回答一下TOP-K问题:即求数据结合中前K个最大的元素或最小的元素,一把情况下数据很大。
2).对于这种场景,首先想到的就是排序,但是:数据非常大,排序就不可取了,因为内存大小的原因,不会全部加载到内存,这时堆就发生了巨大的优势。
思路:利用K个元素建堆,如果是求最大的K个元素,就建立小堆,求最小的K歌元素,就建立大堆。然后用N-K个元素与堆顶元素比较,满足条件就交换。
下面是源码:
void HeapInit(Heap* php)
{assert(php);php->a = NULL;php->size = php->capacity =0;
}void HeapDestroy(Heap* php)
{assert(php);free(php->a);php->a = NULL;php->capacity = php->size =0;
}void Swap(HeapDateType* child, HeapDateType* parent){HeapDateType tmp = *child;*child= *parent;*parent = tmp;
}void AdjustUp(HeapDateType* a,int child){int parent = (child-1)/2;while(child > 0){if(a[child] < a[parent]){Swap(&a[child],&a[parent]);child = parent;parent = (child-1)/2;}else{break;}
}}void HeapPush(Heap* php,HeapDateType x)
{assert(php);if(php->size == php->capacity){int newCapacity = php->capacity == 0?4:php->capacity*2;HeapDateType* tmp = (HeapDateType*)realloc(php->a,sizeof(HeapDateType)*newCapacity);if(tmp == NULL){perror("realloc fail\n");}php->a = tmp;php->capacity = newCapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a,php->size-1);
}void HeapPrint(Heap* php)
{assert(php);for(size_t i =0; i<php->size; i++){std::cout << php->a[i] << " ";}std::cout << std::endl;
}void AdjustDown(HeapDateType* a,int n, int parent)
{int child = parent*2+1;while(child < n){if(child+1 < n && a[child+1] < a[child]){child++;}if(a[child] < a[parent]){Swap(&a[child],&a[parent]);parent = child;child = parent*2+1;}else{break;}}
}HeapDateType HeapTop(Heap* php)
{assert(php);assert(php->size > 0);return php->a[0];
}void HeapPop(Heap* php)
{assert(php);assert(php->size > 0);Swap(&php->a[0],&php->a[php->size-1]);--php->size;AdjustDown(php->a,php->size,0);}bool HeapEmpty(Heap* php)
{assert(php);return php->size == 0;
}
void HeapSort(int* a, int n)
{//向上调整 O(n*logn)
// for(size_t i =1; i<n; i++){
// AdjustUp(a,i);
// }
////向下调整 O(n)for(int i = (n-2)/2; i>=0; i--){AdjustDown(a,n,i);}//时间复杂度O(N*logN)int end = n-1;while(end > 0){Swap(&a[0],&a[end]);AdjustDown(a,end,0);--end;}
}void PrintTopK(const char* filename,int k)
{FILE* fout = fopen(filename,"r");if(fout == NULL){perror("fopen fail");exit(-1);}int* minHeap = (int*)malloc(sizeof(int)*k);if(minHeap == NULL){perror("malloc fail");exit(-1);}for(int i =0; i<k; i++){fscanf(fout,"%d",&minHeap[i]);}for(int i = (k-2)/2; i>=0; i++){AdjustDown(minHeap,k,0);}int x =0;while(fscanf(fout,"%d",&x)!= EOF){if(x > minHeap[0]){minHeap[0] = x;AdjustDown(minHeap,k,0);}}for(int i =0; i<k; i++){std::cout << minHeap[i] << " ";}std::cout << std::endl;
}
相关文章:

数据结构——堆(C语言)
本篇会解决一下几个问题: 1.堆是什么? 2.如何形成一个堆? 3.堆的应用场景 堆是什么? 堆总是一颗完全二叉树堆的某个节点总是不大于或不小于父亲节点 如图,在小堆中,父亲节点总是小于孩子节点的。 如图&a…...

B058-SpringBoot
目录 springboot概念与作用入门案例springboot运行方式热部署配置文件Profile多环境支持整合测试-springboot-testSpringboot-web1.返回json数据2.返回页面(模板技术)thymeleaf1.导入thymeleaf依赖2.模板文件3.controller4.启动类 SSM整合1.导包2.项目目…...
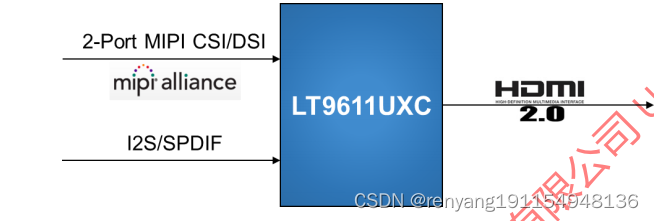
龙迅LT9611UXC 2PORT MIPICSI/DSI转HDMI(2.0)转换器+音频,内置MCU
龙迅LT9611UXC 1.描述: LT9611UXC是一个高性能的MIPI DSI/CSI到HDMI2.0转换器。MIPI DSI/CSI输入具有可配置的单 端口或双端口,1高速时钟通道和1~4高速数据通道,最大2Gbps/通道,可支持高达16Gbps的总带 宽。LT9611UXC支持突发…...
STM32存储左右互搏 I2C总线读写FRAM MB85RC1M
STM32存储左右互搏 I2C总线读写FRAM MB85RC1M 在较低容量存储领域,除了EEPROM的使用,还有铁电存储器FRAM的使用,相对于EEPROM, 同样是非易失性存储单元,FRAM支持更高的访问速度, 其主要优点为没有EEPROM持续写操作跨页…...
1340. 跳跃游戏 V;2039. 网络空闲的时刻;2767. 将字符串分割为最少的美丽子字符串
1340. 跳跃游戏 V 核心思想:动态规划记忆化搜索。定义dfs(i),表示从i开始最多可以访问多少个下标,然后统计往左跳和往右边跳的最大值,思路其实比较简单,但是代码我感觉还是不太好想。 2039. 网络空闲的时刻 核心思想…...
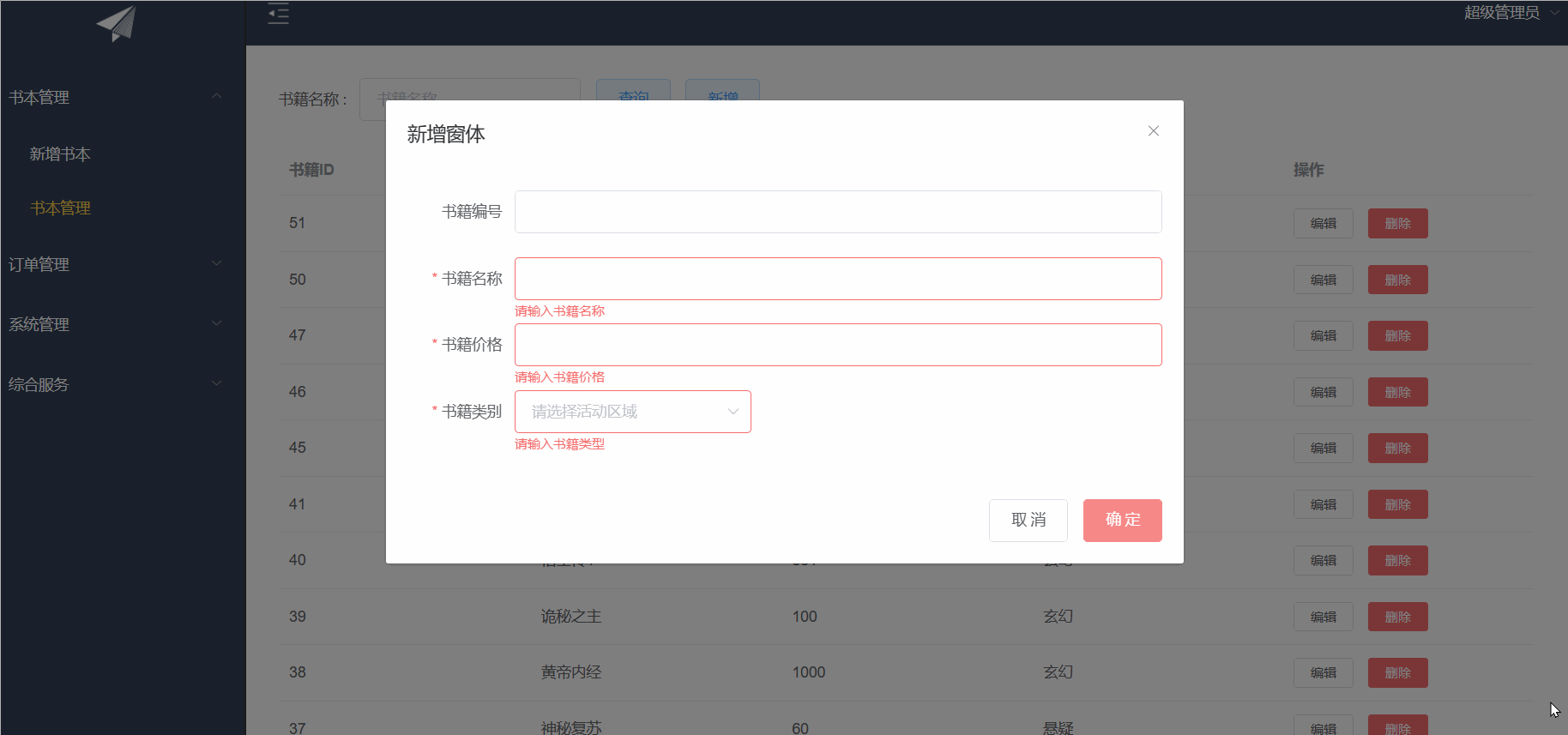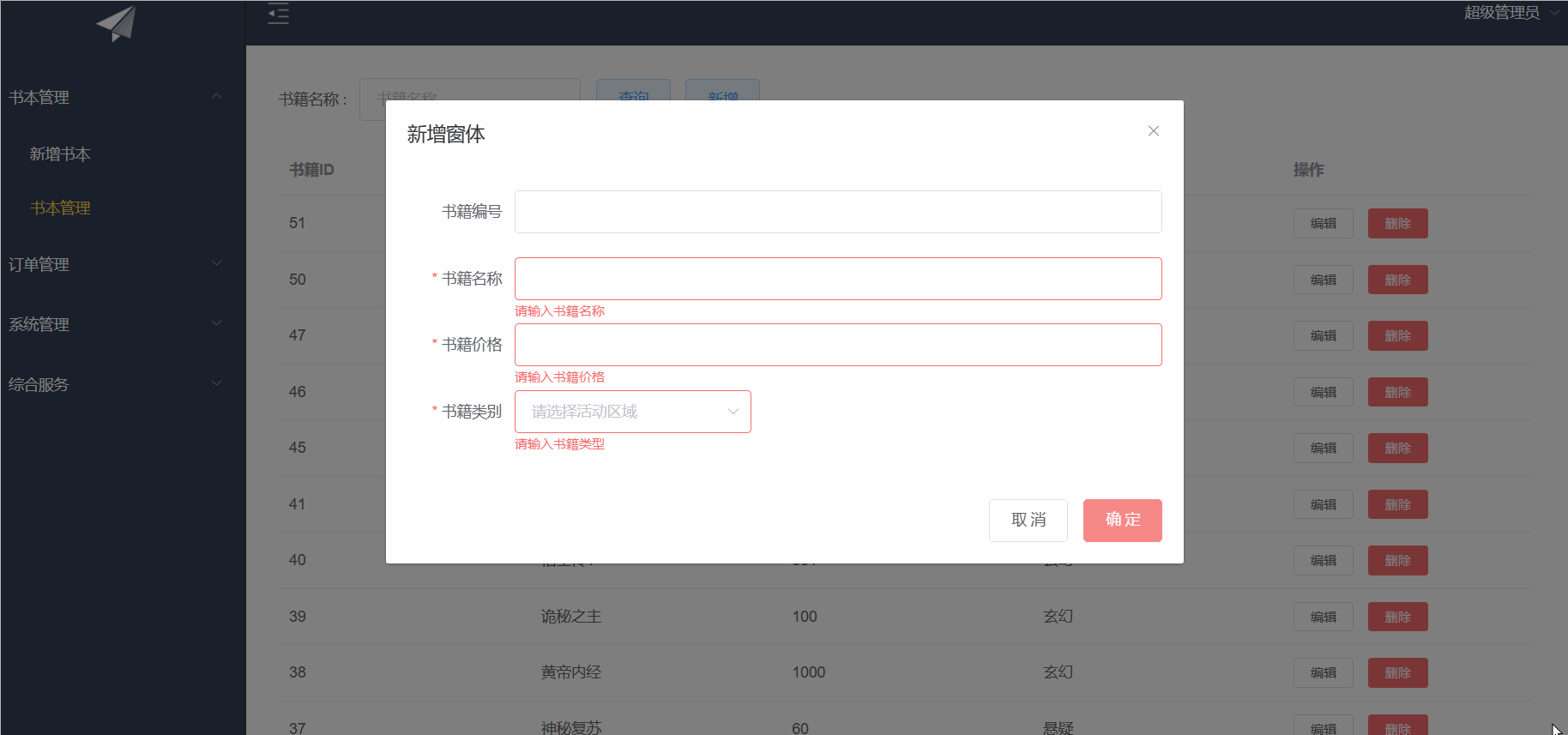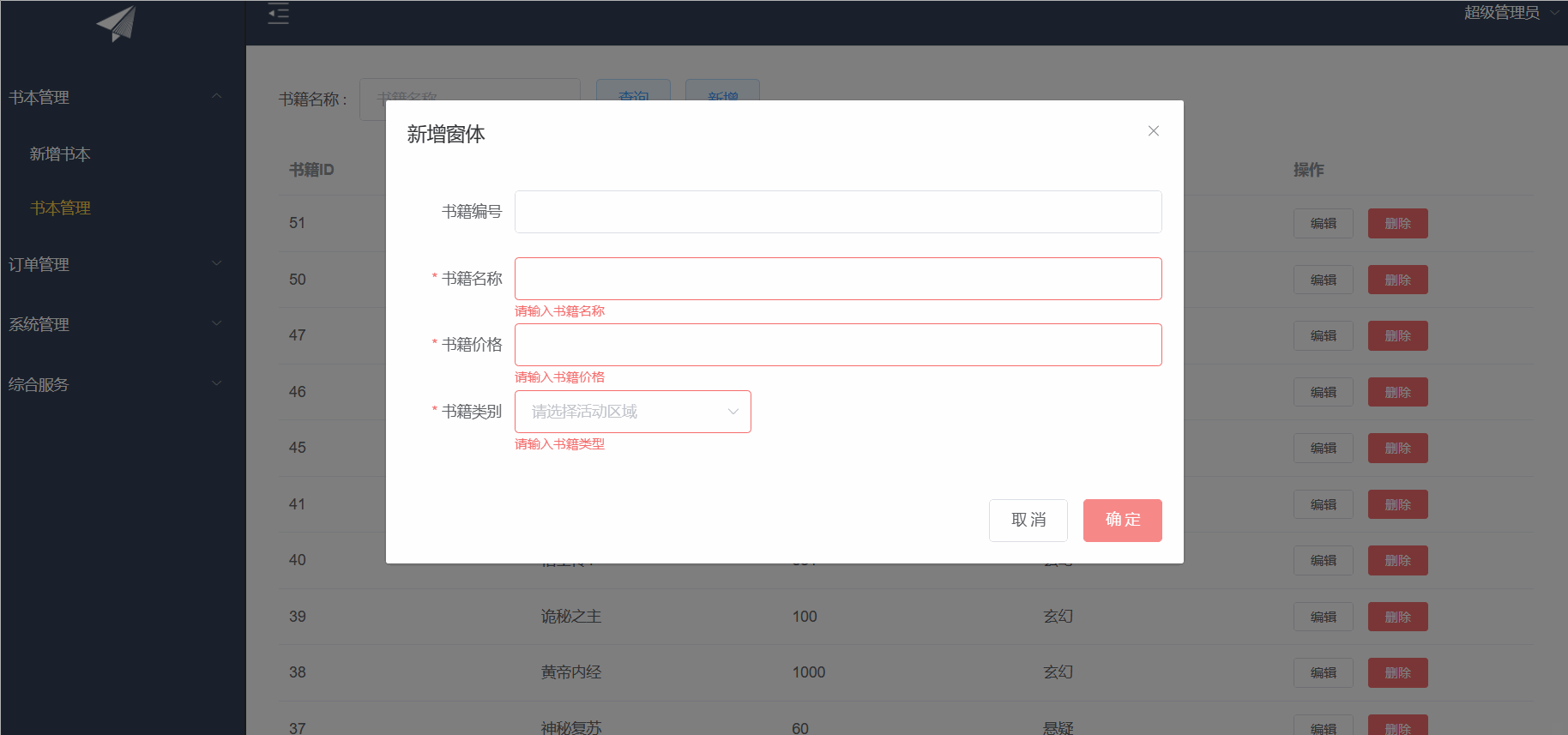
ElementUI之CUD+表单验证
目录 前言: 增删改查 表单验证 前言: 继上篇博客来写我们的增删改以及表单验证 增删改查 首先先定义接口 数据样式,我们可以去elementUI官网去copy我们喜欢的样式 <!-- 编辑窗体 --><el-dialog :title"title" :visib…...

Linux:nginx---web文件服务器
我这里使用的是centos7系统 nginx源码包安装 Linux:nginx基础搭建(源码包)_鲍海超-GNUBHCkalitarro的博客-CSDN博客https://blog.csdn.net/w14768855/article/details/131445878?ops_request_misc%257B%2522request%255Fid%2522%253A%25221…...

go 端口转发 代理V2 --chatGPT
问:broker(localPort, targetPort), 实现远程访问localPort的http代理转发到目标机器 gpt: 要实现一个简单的 HTTP 代理服务器,你可以使用 Go 的 net/http 包来处理 HTTP 请求和响应。以下是一个示例,演示如何创建一个 HTTP 代理服务器将本地…...
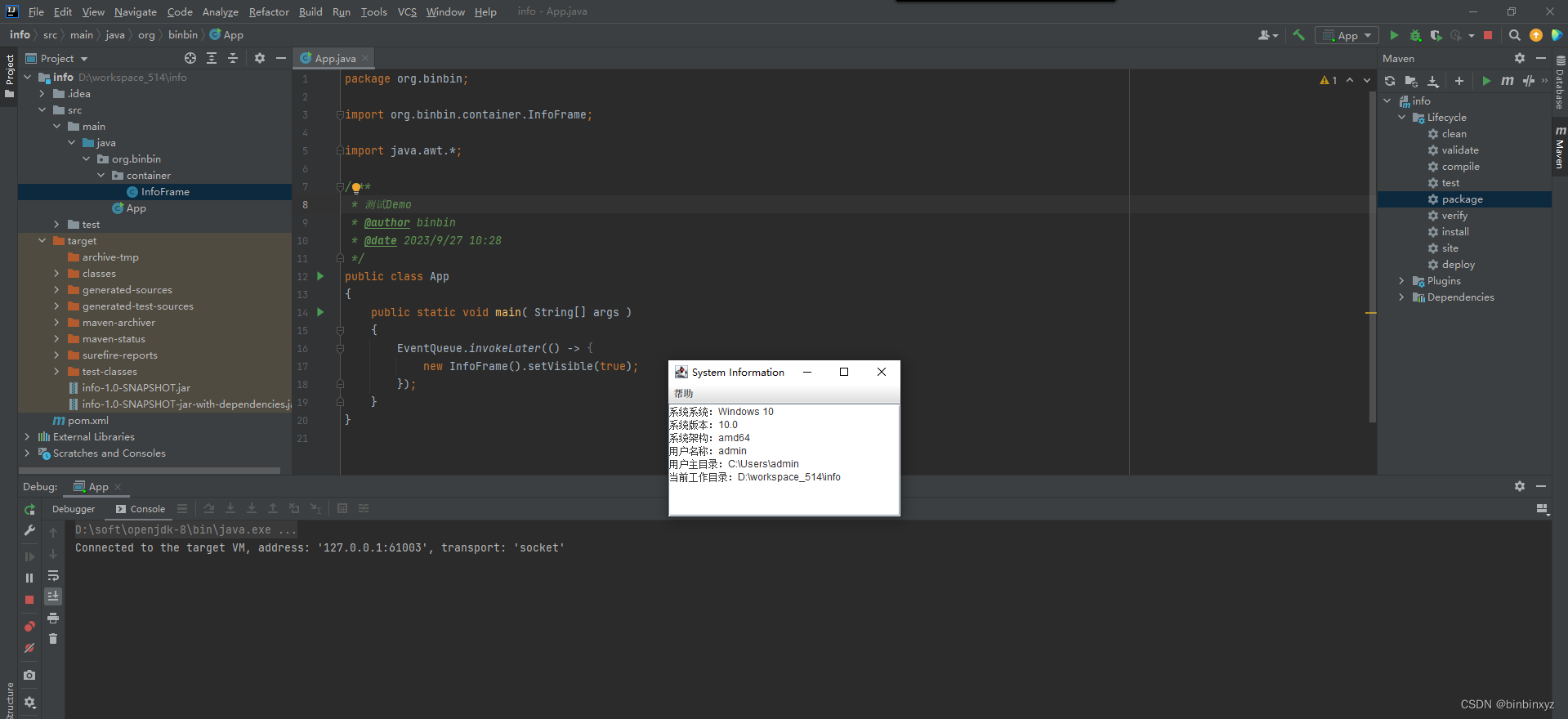
idea环境下如何打包可运行jar?
工作中有时候偶尔写一些工具类、小程序,可是java程序员制作一个可运行jar实在折腾,利用idea开发环境,可以快速打包自己的可运行jar。具体怎么操作呢? 创建一个空白的java项目并完成自己的程序开发 完成java代码: /**…...

基于FFmpeg的Android播放器
基于FFmpeg的Android播放器 文章目录 基于FFmpeg的Android播放器1. 前言2. 编译相关组件库3. 解码器4. 解码流程5. 音频输出6. 视频输出(需要优化) 1. 前言 FFmpeg是一个最有名的开源的编解码库,实现了通常的编解码逻辑。它还能够根据平台特…...

osgPBR(十五)镜面IBL--查看不同级别的HDR环境贴图
首先,设置可以使用Mipmap,启用三线性过滤,设置最大级别和最小级别 osg::ref_ptr<osg::TextureCubeMap> tcm new osg::TextureCubeMap; tcm->setTextureSize(128, 128);tcm->setFilter(osg::Texture::MIN_FILTER, osg::Texture:…...
Docker的学习记录
Docker是一个被广泛使用的开源容器引擎,基于Go语言,遵从Apache2.0协议开源。 docker的三个概念:容器、镜像和仓库。 镜像(Image):镜像是Docker中的一个模板。通过 Docker镜像 来创建 Docker容器ÿ…...

Android Jetpack组件架构:ViewModel的原理
Android Jetpack组件架构:ViewModel的原理 导言 本篇文章是关于介绍ViewModel的,由于ViewModel的使用还是挺简单的,这里就不再介绍其的基本应用,我们主要来分析ViewModel的原理。 ViewModel的生命周期 众所周知,一般…...
学习笔记1.0)
数据分析(python)学习笔记1.0
《利用Python进行数据分析》(原书第2版) 《利用Python进行数据分析》(原书第2版) 《利用Python进行数据分析》(原书第2版) 社区和会议 除了网络搜索,科学、数据相关的Python邮件列表对于解决问题也非常有帮助。可以看看下列邮件列表: pydata:与数据分析和pandas相…...
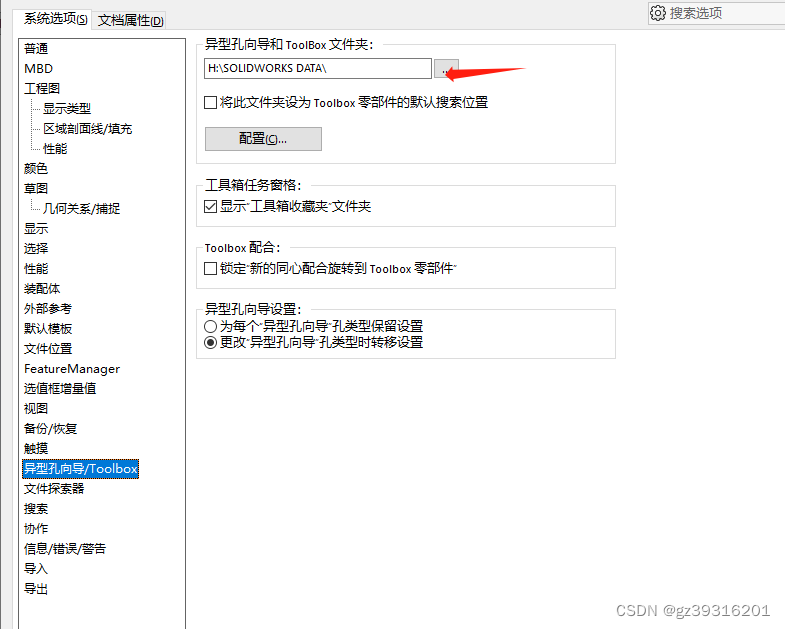
SW免安装的toolbox只读问题
把SOLIDWORKSDATA 整体复制到另外的目录,然后这里设置目录位置。不然原始位置有只读属性...
nodejs在pdf中绘制表格
需求 之前我已经了解过如何在pdf模板中填写字段了 nodejs根据pdf模板填入中文数据并生成新的pdf文件https://blog.csdn.net/ArmadaDK/article/details/132456324 但是当我具体使用的时候,我发现我的模板里面有表格,表格的长度是不固定的,所…...

使用不同尺寸的传感器拍照时,怎么保证拍出同样视场范围的照片?
1、问题背景 使用竞品机做图像效果对比时,我们通常都会要求拍摄的照片要视场范围一致,这样才具有可比性。之前我会考虑用同样焦距、同样分辨率的设备去拍照对比就可以了,觉得相机的视场范围只由镜头焦距来决定。 但如果对于不同尺寸的传感器…...
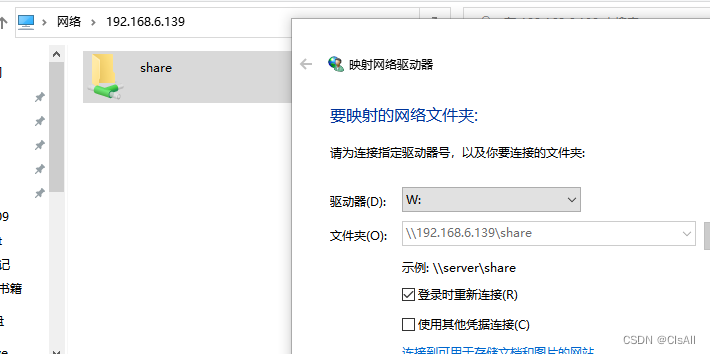
01-工具篇-windows与linux文件共享
一般来说绝大部分PC上装的系统均是windows,为了开发linux程序,会在PC上安装一个Vmware的虚拟机,在虚拟机上安装ubuntu18.04,由于windows上的代码查看软件、浏览器,通信软件更全,我们想只用ubuntu进行编译&a…...
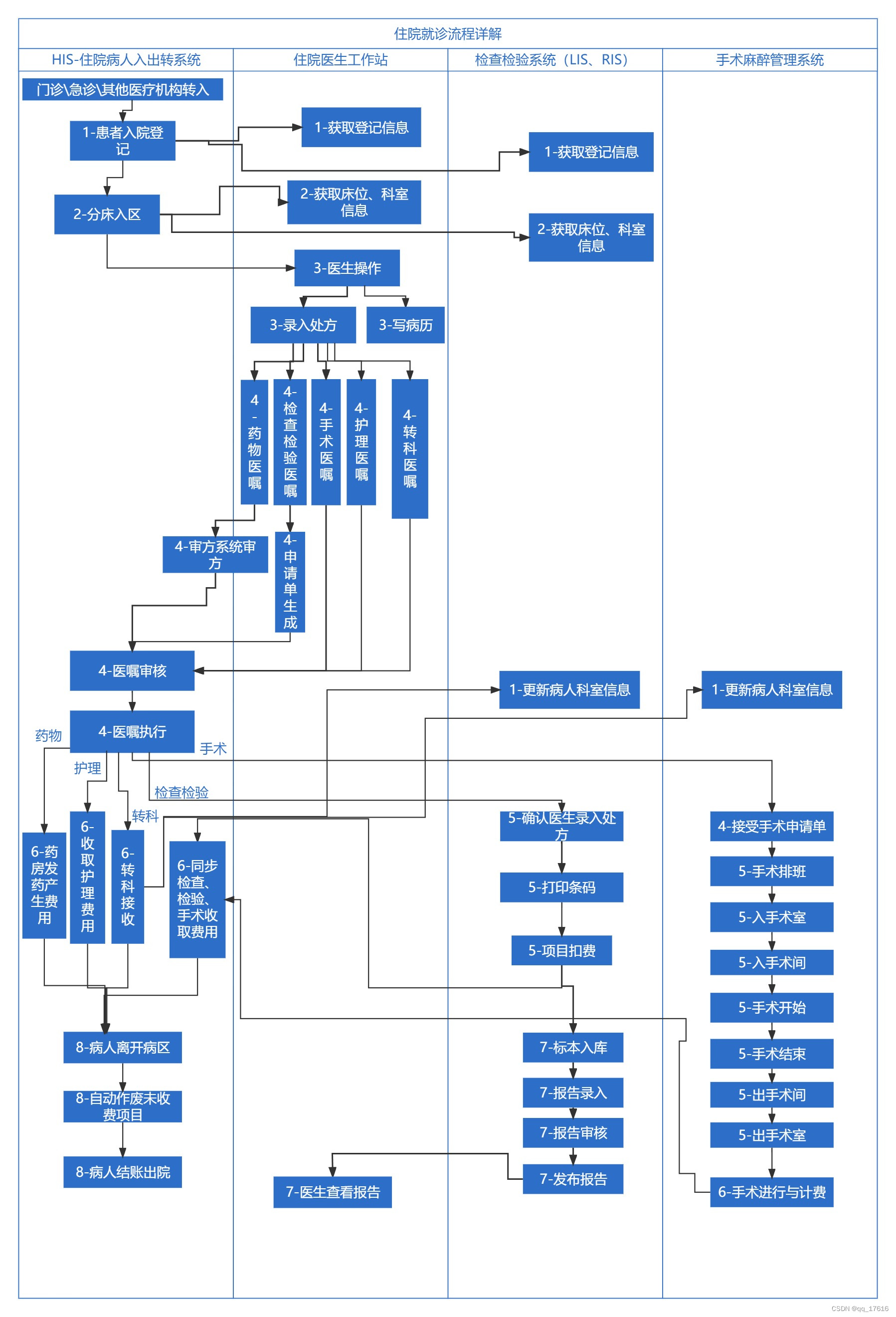
医疗实施-住院流程详解
住院就诊流程详解 1.病人入院登记2.病人进入病区3.医生操作病人4.医嘱录入与审核执行5. 医嘱收费前在对应业务系统的操作5.1.药物医嘱5.2.检查检验医嘱5.3.手术医嘱 6.住院医嘱费用的产生7. 医嘱收费后在对应业务系统的操作8. 病人出院 这篇文章是基于我的文章《医疗实施-住院就…...

本地连接服务器 jupyter notebook
本地连接服务器 jupyter notebook 一、前提工作二、服务器操作三、Windows 操作 一、前提工作 准备一台Linux云服务器新建一个用户,并切换到此用户安装 Anaconda 二、服务器操作 远程服务器上安装和配置 Jupyter Notebook: pip3 install jupyter接着…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...
