CCF CSP认证 历年题目自练Day17
CCF CSP认证 历年题目自练Day17
题目一
试题编号: 201803-1
试题名称: 跳一跳
时间限制: 1.0s
内存限制: 256.0MB
问题描述:
问题描述
近来,跳一跳这款小游戏风靡全国,受到不少玩家的喜爱。
简化后的跳一跳规则如下:玩家每次从当前方块跳到下一个方块,如果没有跳到下一个方块上则游戏结束。
如果跳到了方块上,但没有跳到方块的中心则获得1分;跳到方块中心时,若上一次的得分为1分或这是本局游戏的第一次跳跃则此次得分为2分,否则此次得分比上一次得分多两分(即连续跳到方块中心时,总得分将+2,+4,+6,+8…)。
现在给出一个人跳一跳的全过程,请你求出他本局游戏的得分(按照题目描述的规则)。
输入格式
输入包含多个数字,用空格分隔,每个数字都是1,2,0之一,1表示此次跳跃跳到了方块上但是没有跳到中心,2表示此次跳跃跳到了方块上并且跳到了方块中心,0表示此次跳跃没有跳到方块上(此时游戏结束)。
输出格式
输出一个整数,为本局游戏的得分(在本题的规则下)。
样例输入
1 1 2 2 2 1 1 2 2 0
样例输出
22
数据规模和约定
对于所有评测用例,输入的数字不超过30个,保证0正好出现一次且为最后一个数字。
题目分析(个人理解)
- 常规输入直接放到列表l=list(map(int,input().split()))
再看,输入1就加一分,2第一次出现就加两分,如果连续出现就累加2,即连续跳到方块中心时,总得分将+2,+4,+6,+8… - 那很好办,直接多分支语句就可以解决,我用a作为累加器,sum存放总得分。
- 直接上代码!!!
l=list(map(int,input().split()))
two=0
a=0
for i in range(len(l)):if l[i]==1:sum+=1a=0elif l[i]==2 and a==0:sum+=2a=2elif l[i]==2 and a!=0:a+=2sum+=aelif l[i]==0:break
print(sum)题目二
试题编号: 201803-2
试题名称: 碰撞的小球
时间限制: 1.0s
内存限制: 256.0MB
问题描述:
问题描述
数轴上有一条长度为L(L为偶数)的线段,左端点在原点,右端点在坐标L处。有n个不计体积的小球在线段上,开始时所有的小球都处在偶数坐标上,速度方向向右,速度大小为1单位长度每秒。
当小球到达线段的端点(左端点或右端点)的时候,会立即向相反的方向移动,速度大小仍然为原来大小。
当两个小球撞到一起的时候,两个小球会分别向与自己原来移动的方向相反的方向,以原来的速度大小继续移动。
现在,告诉你线段的长度L,小球数量n,以及n个小球的初始位置,请你计算t秒之后,各个小球的位置。
提示
因为所有小球的初始位置都为偶数,而且线段的长度为偶数,可以证明,不会有三个小球同时相撞,小球到达线段端点以及小球之间的碰撞时刻均为整数。
同时也可以证明两个小球发生碰撞的位置一定是整数(但不一定是偶数)。
输入格式
输入的第一行包含三个整数n, L, t,用空格分隔,分别表示小球的个数、线段长度和你需要计算t秒之后小球的位置。
第二行包含n个整数a1, a2, …, an,用空格分隔,表示初始时刻n个小球的位置。
输出格式
输出一行包含n个整数,用空格分隔,第i个整数代表初始时刻位于ai的小球,在t秒之后的位置。
样例输入
3 10 5
4 6 8
样例输出
7 9 9
样例说明
初始时,三个小球的位置分别为4, 6, 8。
 一秒后,三个小球的位置分别为5, 7, 9。
一秒后,三个小球的位置分别为5, 7, 9。

两秒后,第三个小球碰到墙壁,速度反向,三个小球位置分别为6, 8, 10。
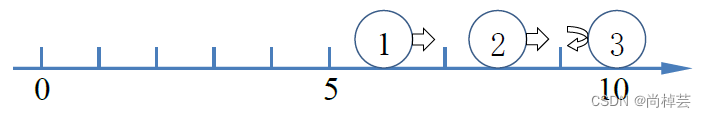
三秒后,第二个小球与第三个小球在位置9发生碰撞,速度反向(注意碰撞位置不一定为偶数),三个小球位置分别为7, 9, 9。

四秒后,第一个小球与第二个小球在位置8发生碰撞,速度反向,第三个小球碰到墙壁,速度反向,三个小球位置分别为8, 8, 10。

五秒后,三个小球的位置分别为7, 9, 9。

样例输入
10 22 30
14 12 16 6 10 2 8 20 18 4
样例输出
6 6 8 2 4 0 4 12 10 2
数据规模和约定
对于所有评测用例,1 ≤ n ≤ 100,1 ≤ t ≤ 100,2 ≤ L ≤ 1000,0 < ai < L。L为偶数。
保证所有小球的初始位置互不相同且均为偶数。
题目分析(个人理解)
- 题目又是又臭又长的感觉,不过意思很好理解,简而言之,将n个小球放到一个长为l的线段上,l是偶数,小球初始位置也是偶数,且开始方向都是向右,每个小球速度相同,碰到边缘或者碰到别的小球就换方向,由于长度和初始位置都是偶数所以不存在三个以及三个小球以上的小球碰撞的情况(题目有提示)。
- 还是先看输入,那就常规操作,都快打烂了。第一行输入n,L,t = list(map(int,input().split()))
- 第二行输入的是n个小球的初始位置positions=list(map(int,input().split()))
- 好!很好!关键的地方来了,注意输出,我们究竟要的是什么?是t时间后的每个小球的位置,我用一个空列表存储小球的运动方向,1表示向右运动,-1就是向左运动,位序就是小球的编号。
- 刚开始小球放上去都是向右运动的, 那直接用append()方法直接追加写入1。
6.== 对于碰撞的情况有三种,第一种,碰到右壁换方向,第二种,碰到左壁换方向,这两种情况很好解决,直接判断positions的值,如果是0意味着碰左壁,大于等于 l 意味着碰右壁,第三种是小球两两碰撞后改变方向,这种情况要注意发生的位置范围==。 - positions的值记录的是每个小球的当前位置,speed的值是动态的,根据碰撞情况确定方向(1或-1),我从第一秒一直遍历到第t秒,再加上初始位置就是小球的最后位置。(这也是输出需要的值)
然后遍历positions列表输出即可!! - 第三种情况怎么解决?positions的位序代表小球编号,值代表位置,注意第三种情况只可能在位置为1到 l-1 位置发生。只有两个小球碰撞的情况,所以直接遍历比较编号为k和k+1的小球的positons的值如果相等我就改变k和k+1小球的运动方向。
- 上代码!!!
n,L,t = list(map(int,input().split()))
positions=list(map(int,input().split()))
speed = []
for i in range(n):speed.append(1)
for j in range(t):for k in range(n):if positions[k] <= 0 or positions[k] >= L:speed[k] = -speed[k]for l in range(k+1,n):if positions[k] == positions[l]:speed[k] = -speed[k]speed[l] = -speed[l]for m in range(n):positions[m] += speed[m]
for o in range(n):print(positions[o],end=" ")总结
在这个最容易躁动的年纪想要沉下心来做忠于自己内心的事情确实是一件难事。——————shangzhaoyun 2023.9.30



相关文章:

CCF CSP认证 历年题目自练Day17
CCF CSP认证 历年题目自练Day17 题目一 试题编号: 201803-1 试题名称: 跳一跳 时间限制: 1.0s 内存限制: 256.0MB 问题描述: 问题描述 近来,跳一跳这款小游戏风靡全国,受到不少玩家的喜爱…...
)
基于Matlab实现多因子选股模型(附上源码+数据)
本文将介绍如何使用MATLAB实现多因子选股模型。我们将使用市盈率和市净率两个因子来进行选股,并通过简单的代码案例来演示该过程。 文章目录 引言简单案例总结源码数据下载 引言 多因子选股模型是一种常用的股票选股方法,通过综合考虑多个因子的信息来…...

【中秋国庆不断更】OpenHarmony多态样式stateStyles使用场景
Styles和Extend仅仅应用于静态页面的样式复用,stateStyles可以依据组件的内部状态的不同,快速设置不同样式。这就是我们本章要介绍的内容stateStyles(又称为:多态样式)。 概述 stateStyles是属性方法,可以根…...
Qt扩展-QCustomPlot绘图基础概述
QCustomPlot绘图基础概述 一、概述二、改变外观1. Graph 类型2. Axis 坐标轴3. 网格 三、案例1. 简单布局两个图2. 绘图与多个轴和更先进的样式3. 绘制日期和时间数据 四、其他Graph:曲线,条形图,统计框图,… 一、概述 本教程使用…...
二、局域网联机
目录 1.下载资源包 2.配置NetworkManager 3.编写测试UI 1.下载资源包 2.配置NetworkManager (1)在Assets/Prefabs下创建Network Prefabs List 相应设置如下: (2) 创建空物体“NetworkManager”并挂载NetworkMan…...

决策树剪枝:解决模型过拟合【决策树、机器学习】
如何通过剪枝解决决策树的过拟合问题 决策树是一种强大的机器学习算法,用于解决分类和回归问题。决策树模型通过树状结构的决策规则来进行预测,但在构建决策树时,常常会出现过拟合的问题,即模型在训练数据上表现出色,…...

Ubuntu部署运行ORB-SLAM2
ORB-SLAM2是特征点法的视觉SLAM集大成者,不夸张地说是必学代码。博主已经多次部署运行与ORB-SLAM2相关的代码,所以对环境和依赖很熟悉,对整个系统也是学习了几个月,一行行代码理解。本次在工控机上部署记录下完整的流程。 ORB-SLA…...
二十,镜面IBL--打印BRDF积分贴图
比起以往,这节应该是最轻松的了, 运行结果如下 代码如下: #include <osg/TextureCubeMap> #include <osg/TexGen> #include <osg/TexEnvCombine> #include <osgUtil/ReflectionMapGenerator> #include <osgDB/Re…...

自动驾驶:未来的道路上的挑战与机遇
自动驾驶:未来的道路上的挑战与机遇 文章目录 引言安全与道路事故的减少交通拥堵的缓解城市规划的变革技术和法律挑战结语 2023星火培训【专项营】Apollo开发者社区布道师倾力打造,包含PnC、新感知等的全新专项课程上线了。理论与实践相结合,…...

Go 语言 iota 的神奇力量
前言 当你深入研究官网库、开源库或者任何一个 Go 项目时,你都会发现 iota 这个神奇的标识符无处不在。它扮演着一种重要的角色,让代码变得更加简洁、清晰,并提高了可读性和可维护性。它的应用范围广泛,从枚举类型到位运算&#…...

前端开发和后端开发的一些建议
前端开发和后端开发是Web开发的两个方向 前端开发主要负责实现用户在浏览器上看到的界面和交互体验,包括HTML、CSS和JavaScript等技术。后端开发主要负责处理服务器端的逻辑和数据,包括数据库操作、服务器配置和接口开发等技术。 前端开发 前端开发需…...
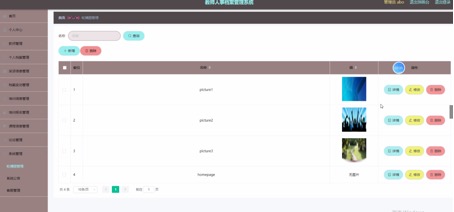
基于 SpringBoot+Vue 的教室人事档案管理系统
1 简介 教师人事档案管理系统利用信息的合理管理,动态的、高效的、安全的实现了教师的各种需求,改变了传统的网上查看方式,使教师可以足不出户的在线查看最适合自己个人档案、奖惩信息、档案变动、培训报名或者新闻资讯。 1、教师后台功能模…...

Lua学习笔记:require非.lua拓展名的文件
前言 本篇在讲什么 Lua的require相关的内容 本篇需要什么 对Lua语法有简单认知 对C语法有简单认知 依赖Visual Studio工具 本篇的特色 具有全流程的图文教学 重实践,轻理论,快速上手 提供全流程的源码内容 ★提高阅读体验★ 👉 ♠…...

Python 编程基础 | 第三章-数据类型 | 3.3、浮点数
一、浮点数...
beego---ORM相关操作
Beego框架是go语言开发的web框架。 **那什么是框架呢?**就是别人写好的代码,我们可以直接使用!这个代码是专门针对某一个开发方向定制的,例如:我们要做一个网站,利用 beego 框架就能非常快的完成网站的开发…...
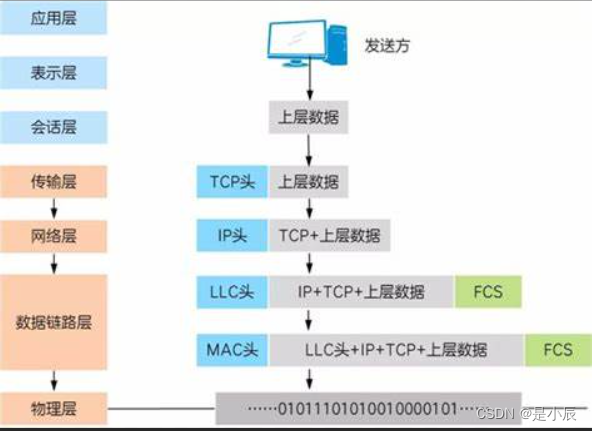
【网络原理】初始网络,了解概念
文章目录 1. 网络通信1.1 局域网LAN1.2 广域网WAN 2. 基础概念2.1 IP2.2 端口号 3. 认识协议4. 五元组5. 协议分层5.1 分层的作用5.2 OSI七层模型5.3 TCP/IP五层(四层)模型 6. 封装和分用 1. 网络通信 计算机与计算机之间是互相独立,是独立模…...
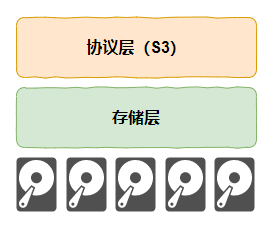
对象存储,从单机到分布式的演进
关于数据存储的相关知识,请大家关注“数据存储张”,各大平台同名。 通过《什么是云存储?从对象存储说起》我们对对象存储的历史、概念和基本使用有了一个大概的认识。而且我们以Minio为例,通过单机部署的模式实际操作了一下对象存储的GUI,感受了一下对象存储的用法。 在上…...
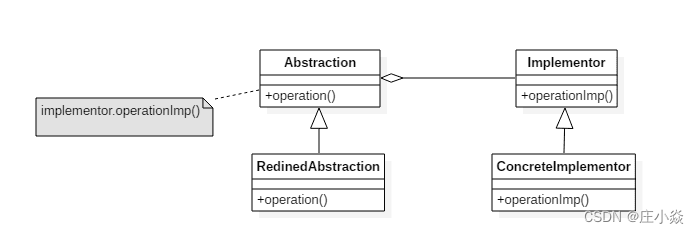
结构型设计模式——桥接模式
摘要 桥接模式(Bridge pattern): 使用桥接模式通过将实现和抽象放在两个不同的类层次中而使它们可以独立改变。 一、桥接模式的意图 将抽象与实现分离开来,使它们可以独立变化。 二、桥接模式的类图 Abstraction: 定义抽象类的接口Implementor: 定义实现类接口 …...

keepalived的vip实现nginx节点的主备
nginx wget http://nginx.org/download/nginx-1.18.0.tar.gz tar zxvf nginx-1.18.0.tar.gzyum install -y gcc gcc-c pcre pcre-devel zlib zlib-devel openssl openssl-devel libnl3-develcd nginx-1.18.0 mkdir -p /usr/local/nginx #需要使用https,在编译时启用…...

C++之std::atomic解决多线程7个问题(二百四)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...
