【面试经典150 | 数组】除自身以外数组的乘积
文章目录
- 写在前面
- Tag
- 题目来源
- 题目解读
- 解题思路
- 方法一:记录左右乘积
- 空间优化
- 写在最后
写在前面
本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更……
专栏内容以分析题目为主,并附带一些对于本题涉及到的数据结构等内容进行回顾与总结,文章结构大致如下,部分内容会有增删:
- Tag:介绍本题牵涉到的知识点、数据结构;
- 题目来源:贴上题目的链接,方便大家查找题目并完成练习;
- 题目解读:复述题目(确保自己真的理解题目意思),并强调一些题目重点信息;
- 解题思路:介绍一些解题思路,每种解题思路包括思路讲解、实现代码以及复杂度分析;
- 知识回忆:针对今天介绍的题目中的重点内容、数据结构进行回顾总结。
Tag
【数组】
题目来源
面试经典150 | 238. 除自身以外数组的乘积

题目解读
给你一个数组 nums,求出每个元素在数组这个集合中补集的乘积,以数组的形式返回答案。
要求:不准使用除法。
解题思路
题目要求不准使用除法,如果可以使用除的话,我们可以计算数组中所有元素的乘积,然后除以相应的数值即可得到答案数组。
既然不能使用除法,我们就老老实实的乘,将每个数左右两侧的数一个一个的乘起来,但是如果不做预处理的话时间复杂度为 O ( n 2 ) O(n^2) O(n2),对于本题的数据量一定超时,因此可以先记录每个位置左、右侧的元素乘积。
方法一:记录左右乘积
我们维护两个数组 L、R 分别记录每个位置左、右侧的所有元素乘积。具体地,L[i] 表示下标 i 左侧所有元素之积,初始 L[0] = 1;R[i] 表示下标 i 右侧所有元素之积,初始 R[n-1] = 1, n n n 为数组 nums 的长度:
- 枚举
i = 1到i = n-1,更新L[i] = nums[i-1] * L[i-1]; - 枚举
i = n-2到i = 1,更新R[i] = nums[i+1] * R[i+1]。
最后,枚举 i = 0 到 i = n-1,更新 ret[i] = L[i] * R[i],返回 ret。
实现代码
class Solution {
public:vector<int> productExceptSelf(vector<int>& nums) {int n = nums.size();vector<int> L(n, 0), R(n, 0);L[0] = 1;for (int i = 1; i < n; ++i) {L[i] = nums[i-1] * L[i-1];}R[n-1] = 1;for (int i = n -2; i >= 0; --i) {R[i] = R[i+1] * nums[i+1];}vector<int> res(n);for (int i = 0; i < n; ++i) {res[i] = L[i] * R[i];}return res;}
};
复杂度分析
时间复杂度: O ( n ) O(n) O(n), n n n 为数组 nums 的长度。
空间复杂度: O ( n ) O(n) O(n)。
空间优化
有一个地方可以优化一下,我们只用一个数组 ret 记作为答案数组,又做为记录每个位置左侧所有元素乘积的数组。
还是 枚举 i = 1 到 i = n-1,更新 ret[i] = nums[i-1] * ret[i-1];接下来用一个变量 R 来记录当前位置后面所有元素的乘积,初始化 R = 1。我们从后往前更新最后的答案数组,ret[i] *= R,然后对 R 进行更新 R *= nums[i]。
这样可以节省一个数组空间。
实现代码
class Solution {
public:vector<int> productExceptSelf(vector<int>& nums) {int n = nums.size();vector<int> ret(n);ret[0] = 1;for (int i = 1; i < n; ++i) {ret[i] = nums[i-1] * ret[i-1];}int R = 1;for (int i = n-1; i >= 0; --i) {ret[i] *= R;R *= nums[i];}return ret;}
};
复杂度分析
时间复杂度: O ( n ) O(n) O(n), n n n 为数组 nums 的长度。
空间复杂度: O ( 1 ) O(1) O(1),使用的答案数组不算做额外的空间。
写在最后
如果文章内容有任何错误或者您对文章有任何疑问,欢迎私信博主或者在评论区指出 💬💬💬。
如果大家有更优的时间、空间复杂度方法,欢迎评论区交流。
最后,感谢您的阅读,如果感到有所收获的话可以给博主点一个 👍 哦。
相关文章:

【面试经典150 | 数组】除自身以外数组的乘积
文章目录 写在前面Tag题目来源题目解读解题思路方法一:记录左右乘积空间优化 写在最后 写在前面 本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更…… 专栏内容以分析题目为主,并附带一些对于本题涉及到…...
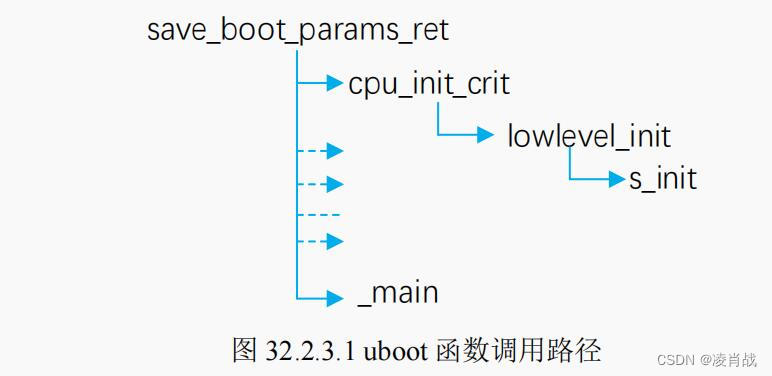
uboot启动流程-涉及s_init汇编函数
一. uboot启动涉及函数 本文简单分析uboot启动流程中,涉及的汇编函数: lowlevel_init函数调用的函数:s_init 函数 save_boot_params_ret函数调用的函数: _main 函数 本文继上一篇文章的学习,地址如下:…...
)
单例模式详解及5种实现方式 (设计模式 一)
基本概念 在软件开发中,单例模式是一种常见的设计模式,用于确保一个类只有一个实例,并提供全局访问点。单例模式在需要确保只有一个对象实例存在的场景中非常有用,例如数据库连接、线程池、日志记录器等。 单例模式的核心思想是通…...
)
面试系列 - Java常见算法(一)
目录 一、排序算法 1、冒泡排序(Bubble Sort): 2、快速排序(Quick Sort): 二、查找算法 1、二分查找(Binary Search): 三、 图算法 1、深度优先搜索(De…...

Sentinel学习(1)——CAP理论,微服务中的雪崩问题,和Hystix的解决方案 Sentinel的相关概念 + 下载运行
前言 Sentinel 是面向分布式、多语言异构化服务架构的流量治理组件,主要以流量为切入点,从流量路由、流量控制、流量整形、熔断降级、系统自适应过载保护、热点流量防护等多个维度来帮助开发者保障微服务的稳定性。 本篇博客介绍CAP理论,微…...

C#学习 - 表达式、语句
表达式 定义 算法逻辑的最基本单元,表达一定的算法意图是由一个或多个操作数和零个或多个操作符组成的序列表达式功能是求值,得到的结果可能是一个值、对象、方法或名称空间因为操作符有优先级,所以表达式也有优先级 分类 一个值。表达式…...

VirtualBox 进入虚拟机后,鼠标出不来了
VirtualBox 进入虚拟机后,鼠标出不来了。 一般情况下,VirtualBox默认的鼠标切换快捷键是右边的Ctrl键。 如果按住右Ctrl键还是没有用,那应该是没有设置主机键。 设置方法: 打开VirtualBox的全局设定,找到热键ÿ…...
)
030-从零搭建微服务-消息队列(二)
写在最前 如果这个项目让你有所收获,记得 Star 关注哦,这对我是非常不错的鼓励与支持。 源码地址(后端):mingyue: 🎉 基于 Spring Boot、Spring Cloud & Alibaba 的分布式微服务架构基础服务中心 源…...

Docker从认识到实践再到底层原理(九)|Docker Compose 容器编排
前言 那么这里博主先安利一些干货满满的专栏了! 首先是博主的高质量博客的汇总,这个专栏里面的博客,都是博主最最用心写的一部分,干货满满,希望对大家有帮助。 高质量博客汇总 然后就是博主最近最花时间的一个专栏…...

操作EXCEL计算3万条数据的NDVI并填入
Python操作EXCEL,计算3万条数据的NDVI并填入 问题描述 现在是有构建好了的查找表,不过构建了3万条数据,在excel中手动计算每行的NDVI值太麻烦了,也不会操作。 就试试python吧,毕竟python自动处理大型EXCEL数据很方便…...
Linux服务器安装Anaconda 配置远程jupyter lab使用虚拟环境
参考的博客: Linux服务器安装Anaconda 并配置远程jupyter lab anaconda配置远程访问jupyter,并创建虚拟环境 理解和创建:Anaconda、Jupyterlab、虚拟环境、Kernel 下边是正文了。 https://www.anaconda.com/download是官网网址,可…...
)
R语言实现随机生存森林(3)
常见问题解答 1、计算C指数 1-Error rate,或者 rsf.err <- get.cindex(yvar$Survival_months,yvar$OS,predictedrf.grow$predicted) 2、模型中predicted和predicted.oob区别 predicted和predicted.oob是两个不同的属性,它们分别表示模型的预测结果…...
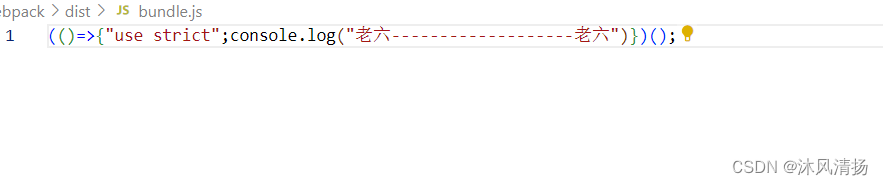
WebPack-打包工具
从图中我们可以看出,Webpack 可以将多种静态资源 js、css、less 转换成一个静态文件,减少了页面的请求. 下面举个例子 : main.js 我们只命名导出一个变量 export const name"老六"index.js import { name } from "./tset/…...

CISSP学习笔记:PKI和密码学应用
第七章 PKI和密码学应用 7.1 非对称密码学 对称密码系统具有共享的秘钥系统,从而产生了安全秘钥分发的问题非对称密码学使用公钥和私钥对,无需支出复杂密码分发系统 7.1.1 公钥与私钥 7.1.2 RSA(兼具加密和数字签名) RSA算法…...

简述Java21新特性
Java21新特性 你发任你发我用Java8 不管Java更新了多少版本,我还是用Java8,因为在很多框架不知道支持不支持Java21,而且因为很多Jar包的版本冲突问题,所以我还是用Java8,但是对于新技术的了解是非常必要的。 Java 21是新推出的长…...
)
Composition API(常用部分)
1. Composition API(常用部分) 文档: https://composition-api.vuejs.org/zh/api.html 1) setup 新的option, 所有的组合API函数都在此使用, 只在初始化时执行一次函数如果返回对象, 对象中的属性或方法, 模板中可以直接使用2) ref 作用: 定义一个数据的响应式语法: cons…...
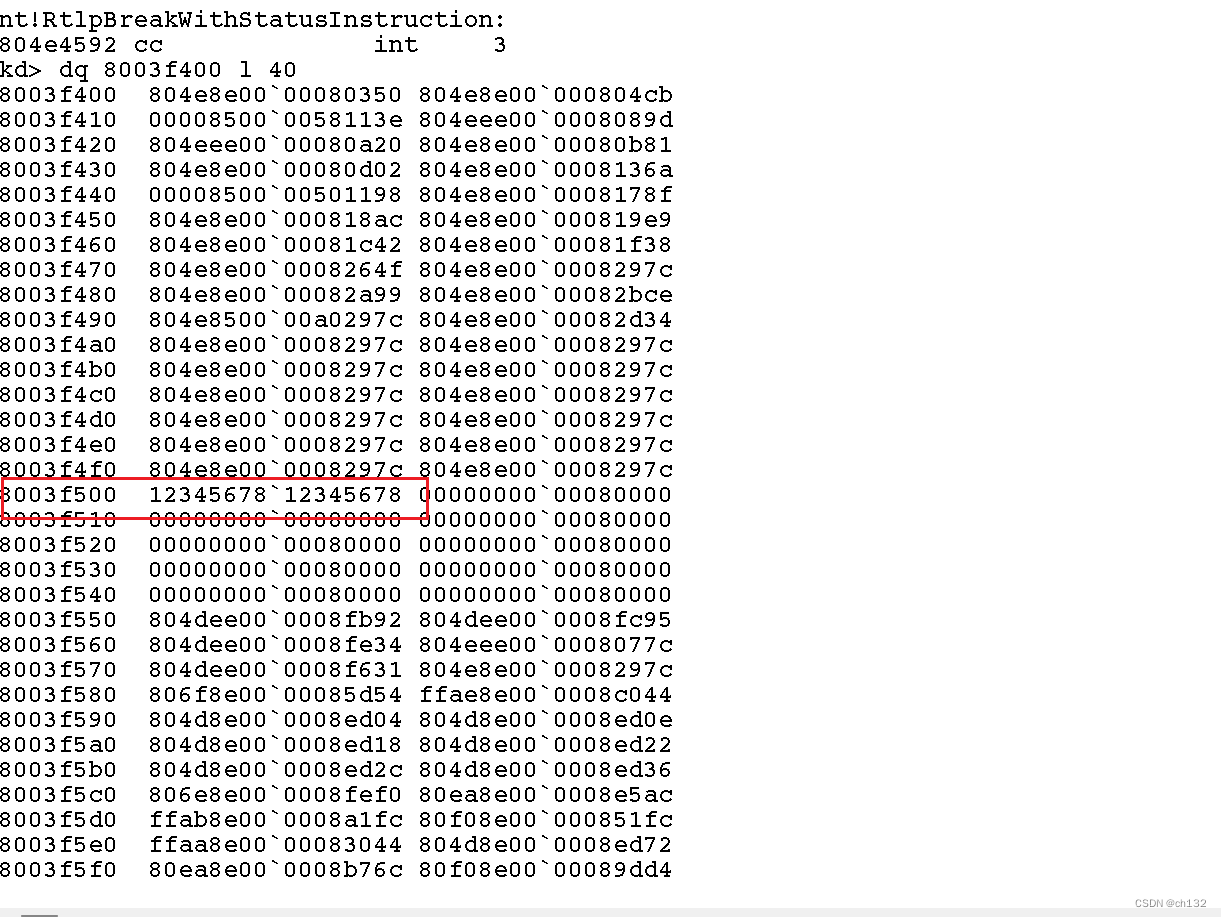
驱动插入中断门示例代码
驱动插入中断描述符示例代码 最近做实验,每次在应用层代码写测试代码的时候都要手动挂一个中断描述符,很不方便所以就想着写个驱动挂一个中断门比较省事 驱动测试效果如下: 下面的代码是个架子,用的时候找个驱动历程传递你要插…...

1 论文笔记:Efficient Trajectory Similarity Computation with ContrastiveLearning
2022CIKM 1 intro 1.1 背景 轨迹相似度计算是轨迹分析任务(相似子轨迹搜索、轨迹预测和轨迹聚类)最基础的组件之一现有的关于轨迹相似度计算的研究主要可以分为两大类: 传统方法 DTW、EDR、EDwP等二次计算复杂度O(n^2)缺乏稳健性 会受到非…...

如何做一个基于 Python 的搜索引擎?
怎么做一个基于 python 的搜索引擎? 1、确定搜索引擎范围和目标用户 在决定做一个基于Python的搜索引擎之前,首先需要确定搜索引擎的范围和目标用户。搜索引擎的范围可以包括新闻、商品、音乐等,不同的领域需要不同的数据来源和处理方式。同…...
Python报错:KeyError: ‘820‘
Python报错:KeyError: ‘820’ 问题描述 原因 操作的表格列名是数字 NIRdata[820] Rdata[630]以上是出错行,dataframe的这种索引方式不支持用数字。 解决方案 先修改列名为字符 然后将出错行改为对应列名 NIRdata[nir] Rdata[r]...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

WEB3全栈开发——面试专业技能点P4数据库
一、mysql2 原生驱动及其连接机制 概念介绍 mysql2 是 Node.js 环境中广泛使用的 MySQL 客户端库,基于 mysql 库改进而来,具有更好的性能、Promise 支持、流式查询、二进制数据处理能力等。 主要特点: 支持 Promise / async-await…...

起重机起升机构的安全装置有哪些?
起重机起升机构的安全装置是保障吊装作业安全的关键部件,主要用于防止超载、失控、断绳等危险情况。以下是常见的安全装置及其功能和原理: 一、超载保护装置(核心安全装置) 1. 起重量限制器 功能:实时监测起升载荷&a…...

Linux操作系统共享Windows操作系统的文件
目录 一、共享文件 二、挂载 一、共享文件 点击虚拟机选项-设置 点击选项,设置文件夹共享为总是启用,点击添加,可添加需要共享的文件夹 查询是否共享成功 ls /mnt/hgfs 如果显示Download(这是我共享的文件夹)&…...
