36.骑士周游算法及其基于贪心算法的优化
概述
骑士周游算法,叫做“马踏棋盘算法”或许更加直观。在国际象棋8x8的棋盘中,马也是走“日字”进行移动,相应的产生了一个问题:“如果要求马 在每个方格只能进入一次,走遍全部的64个方格需要如何行进?”这就是著名的 骑士周游算法的由来。
思路
相信大家看到这个问题首先想到就是回溯。
马踏棋盘问题(骑士周游问题) 实际上是图的深度优先搜索(DFS)的应用。
如果使用回溯(就是深度优先搜索) 来解决,假如马儿踏了53个点,走到了第53个,坐标(1,0),发现已经走到尽头,没办法,那就只能回退了,查看其他的路径,就在棋盘上不停的回溯。
基于回溯的解决方案
- 创建棋盘chessBoard,是一个二维数组;
- 将当前位置设置为已经访问,然后根据当前位置,计算马还能走哪些位置,并放入到一个集合中(ArrayList),最多有8个位置,每走一步,就使用step+1;
- 遍历arrayList中存放的所有位置,看看哪个可以走通;
- 判断马儿是否完成了任务,使用step和应该走的步数(即棋盘格子数-1)比较,如果没有达到数量,则表示没有完成任务,将整个棋盘置0;
注:马 不同的走法(策略),会得到不同的结果,效率也会有影响(优化)。
代码实现
public class HorseChessBoard {private static int X;//棋盘的列数private static int Y;//棋盘的行数//创建一个数组, 标记棋盘的各个位置是否被访问过private static boolean visited[];//试用一个属性,标记是否棋盘的所有位置都被访问过了private static boolean finished;//如果为true,表示成功public static void main(String[] args) {System.out.println("开始执行骑士周游算法~");//测试X = 8;Y = 8;int row = 1;//马儿初始位置的行,从1开始编号int column = 1;//马儿初始位置的列,从1开始编号//创建棋盘int[][] chessboard = new int[X][Y];visited = new boolean[X*Y];//初始值都是false//测试一下耗时long start = System.currentTimeMillis();traversalCheessBoard(chessboard,row-1,column-1,1);long end = System.currentTimeMillis();System.out.println("共耗时"+(end - start)+"ms");//输出棋盘的最终状况for (int[] rows : chessboard) {for (int step : rows) {System.out.print(step+"\t");}System.out.println();}System.out.println("骑士周游算法结束");}/*** 骑士周游问题算法* @param chessBoard 棋盘* @param row 马儿当前位置的行 从0开始* @param column 马儿当前位置的列 从0开始* @param step 是第几步,初始位置是第1步*/public static void traversalCheessBoard(int[][] chessBoard,int row,int column,int step){chessBoard[row][column] = step;//row = 4; X=8; column=4; 4*8+4=36;visited[row*X+column] = true;//标记该位置已经访问//获取当前位置可以走的下一个位置的集合ArrayList<Point> ps = next(new Point(column, row));//遍历pswhile (!ps.isEmpty()){Point p = ps.remove(0);//取出下一个可以走的位置//判断该点是否已经访问过if(!visited[p.y*X+p.x]){//说明还没访问过traversalCheessBoard(chessBoard,p.y,p.x,step+1);}}//判断马儿是否完成了任务,使用step和应该走的步数(即棋盘格子数-1)比较,//如果没有达到数量,则表示没有完成任务,将整个棋盘置0;//说明: step<X*Y成立的情况有两种//1.棋盘到目前位置,仍然没有走完//2.棋盘处于回溯过程if (step<X*Y&&!finished){chessBoard[row][column]=0;visited[row * X + column] = false;}else {finished = true;}}/*** 根据当前位置(Point) ,计算马儿还能走哪些位置(Point),并放入到一个集合中(ArrayList),最多有八个位置* @param curPoint* @return*/public static ArrayList<Point> next(Point curPoint){//创建一个ArrayListArrayList<Point> ps = new ArrayList<>();//创建一个PointPoint p1 = new Point();//判断马儿下一步是否可以走,若可以,将这个位置放入集合//判断马儿是否可以走 位置5if ((p1.x=curPoint.x-2)>=0 && (p1.y = curPoint.y-1)>=0){ps.add(new Point(p1));}//判断马儿是否可以走 位置6if ((p1.x=curPoint.x-1)>=0 && (p1.y = curPoint.y-2)>=0){ps.add(new Point(p1));}//判断马儿是否可以走 位置7if ((p1.x=curPoint.x+1) < X && (p1.y = curPoint.y-2)>=0){ps.add(new Point(p1));}//判断马儿是否可以走 位置0if ((p1.x=curPoint.x+2) < X && (p1.y = curPoint.y-1)>=0){ps.add(new Point(p1));}//判断马儿是否可以走 位置1if ((p1.x=curPoint.x+2) < X && (p1.y = curPoint.y+1)< Y){ps.add(new Point(p1));}//判断马儿是否可以走 位置2if ((p1.x=curPoint.x+1)<X && (p1.y = curPoint.y+2)<Y){ps.add(new Point(p1));}//判断马儿是否可以走 位置3if ((p1.x=curPoint.x-1)>=0 && (p1.y = curPoint.y+2)<Y){ps.add(new Point(p1));}//判断马儿是否可以走 位置4if ((p1.x=curPoint.x-2)>=0 && (p1.y = curPoint.y+1)<Y){ps.add(new Point(p1));}return ps;}
}
效率分析
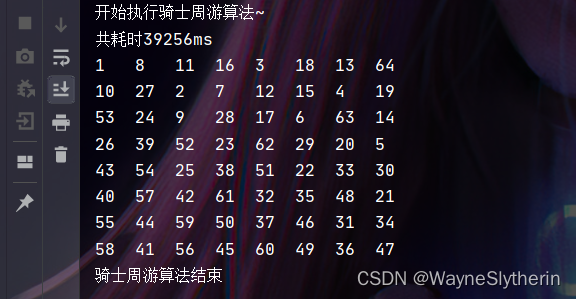
采用回溯的方案思路上自然是可行的,那么它的效率究竟如何呢?可以说很不乐观!测算下来差不多要40秒左右,优化的空间很大。
回溯分析与贪心优化
我们思考可以在此思考一下上面解决方案的是否有可以优化的地方?能否用贪心算法进行优化呢?
- 我们获取当前位置,可以走的下一个位置的集合:
ArrayList ps = next(new Point(column,row)); - 需要对ps中所有Point 下一步的所有集合数目进行非递减排序;
a. 递减是:9,7,6,5,4…
b. 递增排序:4,5,6,7,8…
c. 非递减排序: 1,2,2,3,3,4,4,4,4,4,4,4,5,8,10…
d. 非递增排序: 9,9,9,8,7,5,3… - 如果下一步的选择越少,意味着回溯时的步骤越少,相应的效率也会越高,所以我们应该采用非递减排序,使得回溯的代价尽可能的低。
核心优化代码
我们不妨编写一个方法,根据当前这一步的所有下一步的选择位置,进行非递减排序,以求减少回溯的次数
public static void sort(ArrayList<Point> ps){ps.sort(new Comparator<Point>(){@Overridepublic int compare(Point o1, Point o2) {//获取到o1的下一步的所有位置个数int count1 = next(o1).size();//获取到o2的下一步的所有位置个数int count2 = next(o2).size();if (count1<count2){return -1;}else if (count1==count2){return 0;}else {return 1;}}});}
这样,在上面的回溯算法中,我们可以先对ps进行排序处理,再进行后面的测算
//获取当前位置可以走的下一个位置的集合ArrayList<Point> ps = next(new Point(column, row));//对ps进行排序,排序的规则就是对ps的所有的Point对象的下一步的位置数目进行非递减排序sort(ps);//遍历pswhile (!ps.isEmpty()){Point p = ps.remove(0);//取出下一个可以走的位置//判断该点是否已经访问过if(!visited[p.y*X+p.x]){//说明还没访问过traversalCheessBoard(chessBoard,p.y,p.x,step+1);}}
效率分析
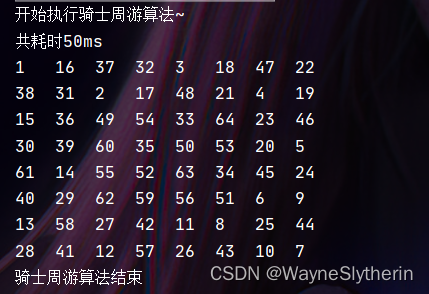
经过贪心算法的优化后,相同的配置下,测算时间直接降到了50ms,效率比之前提升600倍。还是很可观的提升的。
小结
本节,先是采用回溯算法对骑士周游问题进行了拆解,而后利用贪心算法对回溯算法进行了优化解决了骑士周游问题。相信借此我们对贪心算法的应用应该都有了更深层次的理解,算法千万条,应用第一条,只有在合适的场景才能发挥出其最大的作用。
关注我,共同进步,每周至少一更。——Wayne
相关文章:

36.骑士周游算法及其基于贪心算法的优化
概述 骑士周游算法,叫做“马踏棋盘算法”或许更加直观。在国际象棋8x8的棋盘中,马也是走“日字”进行移动,相应的产生了一个问题:“如果要求马 在每个方格只能进入一次,走遍全部的64个方格需要如何行进?”…...

win安装vscode
一,下载 链接如下(64位的):https://az764295.vo.msecnd.net/stable/abd2f3db4bdb28f9e95536dfa84d8479f1eb312d/VSCodeSetup-x64-1.82.2.exe (其他版本看:Download Visual Studio Code - Mac, Linux, Win…...
【图像分割】图像检测(分割、特征提取)、各种特征(面积等)的测量和过滤(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

Linux内核存在缺陷发行陷困境
导读Linux内核已经修复了本地特权esclation缺陷,但是几个上游分发版本例如Red Hat,Canonical和Debian发行版尚未发布更新。管理员应计划减轻Linux服务器和工作站本身的漏洞,并监控其更新计划的发布。 内核缺陷仍存在 在Linux内核4.10.1(CVE-…...
通过java向jar写入新文件
文章目录 原始需求分析实施步骤引入依赖核心编码运行效果 原始需求 有网友提问: 我想在程序中动态地向同一个jar包中添加文件,比如,我的可执行jar包是test.jar,我要在它运行时生成一些xml文件并将这些文件添加到test.jar中,请问如何实现&…...
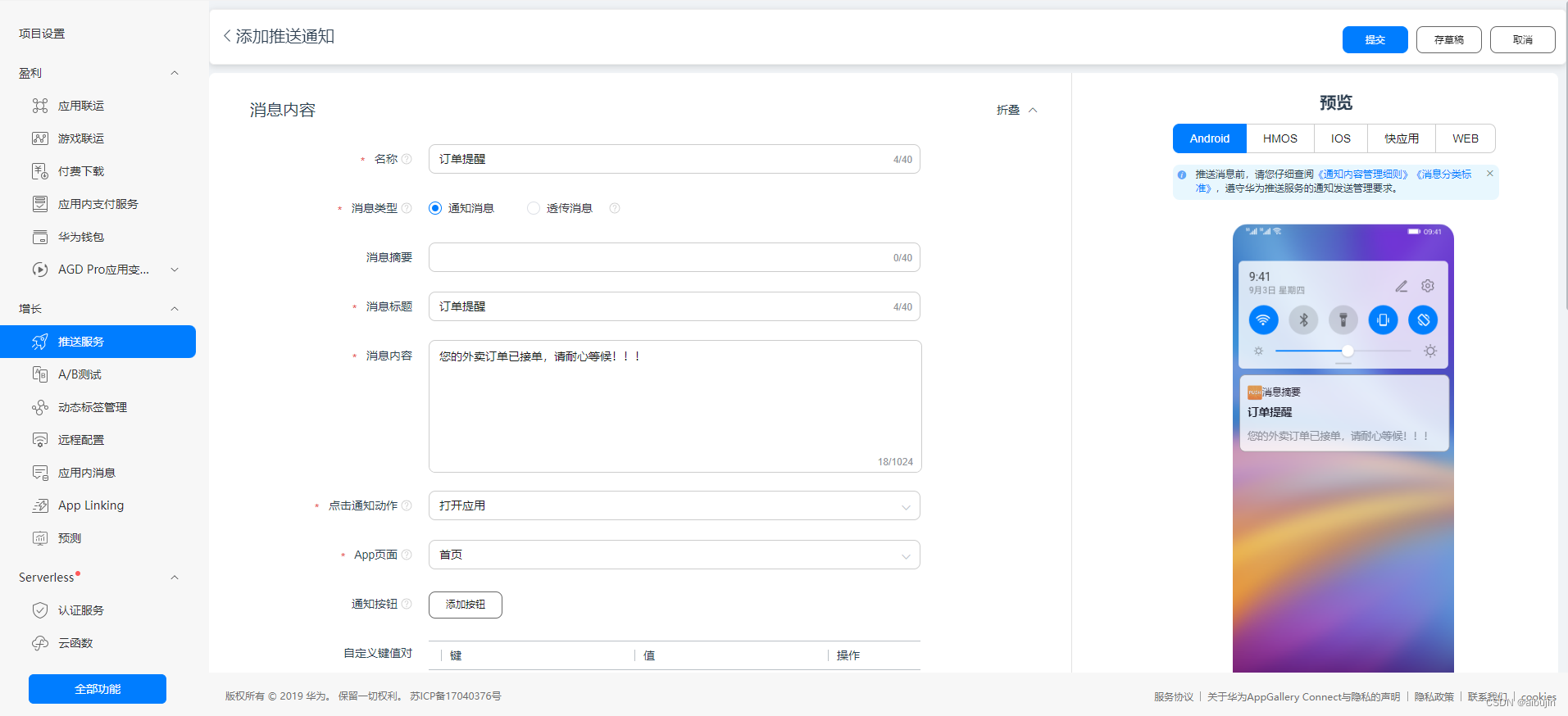
uni-app_消息推送_华为厂商_unipush离线消息推送
文章目录 一、创建项目二、生成签名证书三、开通 unipush 推送服务四、客户端集成四、制作自定义调试基座五、开发者中心后台Web页面推送(仅支持在线推送)六、离线消息推送1、创建华为开发者账号2、开通推送服务3、创建项目4、添加应用5、添加SHA256证书…...

单元测试框架-Pytest(简单学习)
单元测试框架-Pytest Pytest是基于Python语言的单元测试框架,也是一个命令行的工具,比 unittest 测试框架更灵活。具有以下特点: 入门简单,易上手,官方文档丰富而且使用广泛,有大量的参数例子。 unittest…...
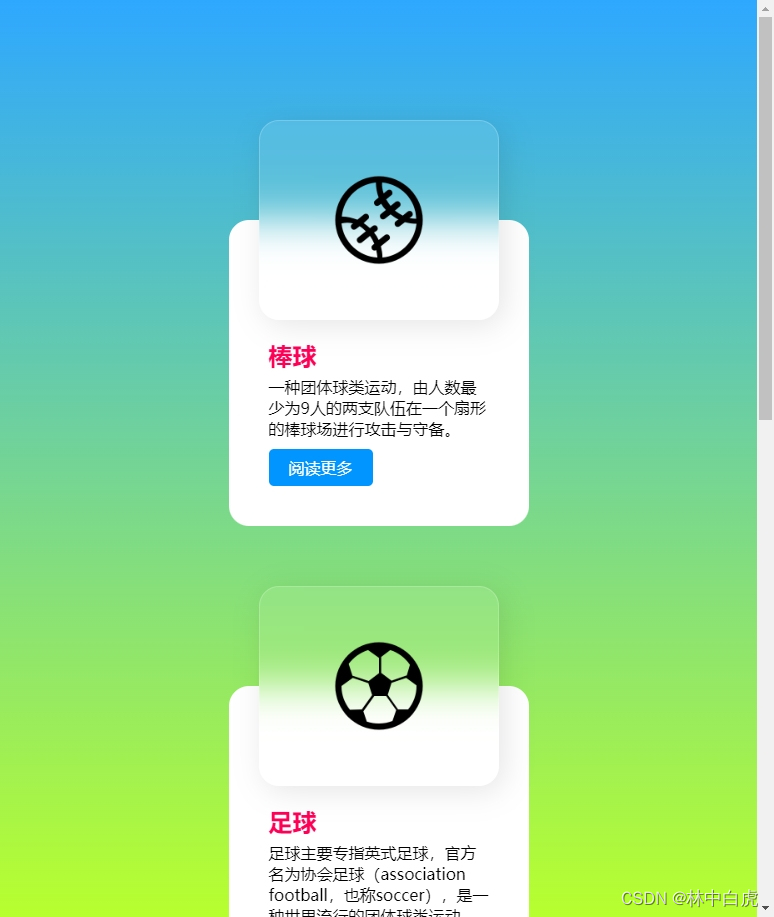
毛玻璃态卡片悬停效果
效果展示 页面结构组成 页面的组成部分主要是卡片。其中卡片的组成部分主要是包括了图片和详情。 卡片的动效是鼠标悬停在卡片上时,图片会移动到左侧,并且图片是毛玻璃效果。所以我们在布局的时候图片会采用绝对布局。而详情则是基础布局。 CSS3 知识…...

【面试经典150 | 数组】除自身以外数组的乘积
文章目录 写在前面Tag题目来源题目解读解题思路方法一:记录左右乘积空间优化 写在最后 写在前面 本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更…… 专栏内容以分析题目为主,并附带一些对于本题涉及到…...
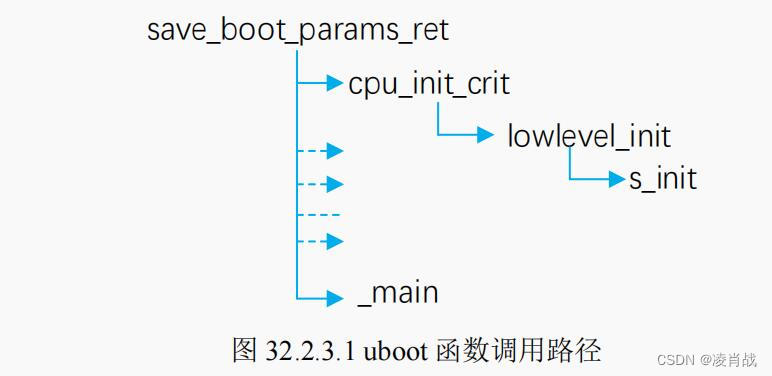
uboot启动流程-涉及s_init汇编函数
一. uboot启动涉及函数 本文简单分析uboot启动流程中,涉及的汇编函数: lowlevel_init函数调用的函数:s_init 函数 save_boot_params_ret函数调用的函数: _main 函数 本文继上一篇文章的学习,地址如下:…...
)
单例模式详解及5种实现方式 (设计模式 一)
基本概念 在软件开发中,单例模式是一种常见的设计模式,用于确保一个类只有一个实例,并提供全局访问点。单例模式在需要确保只有一个对象实例存在的场景中非常有用,例如数据库连接、线程池、日志记录器等。 单例模式的核心思想是通…...
)
面试系列 - Java常见算法(一)
目录 一、排序算法 1、冒泡排序(Bubble Sort): 2、快速排序(Quick Sort): 二、查找算法 1、二分查找(Binary Search): 三、 图算法 1、深度优先搜索(De…...

Sentinel学习(1)——CAP理论,微服务中的雪崩问题,和Hystix的解决方案 Sentinel的相关概念 + 下载运行
前言 Sentinel 是面向分布式、多语言异构化服务架构的流量治理组件,主要以流量为切入点,从流量路由、流量控制、流量整形、熔断降级、系统自适应过载保护、热点流量防护等多个维度来帮助开发者保障微服务的稳定性。 本篇博客介绍CAP理论,微…...

C#学习 - 表达式、语句
表达式 定义 算法逻辑的最基本单元,表达一定的算法意图是由一个或多个操作数和零个或多个操作符组成的序列表达式功能是求值,得到的结果可能是一个值、对象、方法或名称空间因为操作符有优先级,所以表达式也有优先级 分类 一个值。表达式…...

VirtualBox 进入虚拟机后,鼠标出不来了
VirtualBox 进入虚拟机后,鼠标出不来了。 一般情况下,VirtualBox默认的鼠标切换快捷键是右边的Ctrl键。 如果按住右Ctrl键还是没有用,那应该是没有设置主机键。 设置方法: 打开VirtualBox的全局设定,找到热键ÿ…...
)
030-从零搭建微服务-消息队列(二)
写在最前 如果这个项目让你有所收获,记得 Star 关注哦,这对我是非常不错的鼓励与支持。 源码地址(后端):mingyue: 🎉 基于 Spring Boot、Spring Cloud & Alibaba 的分布式微服务架构基础服务中心 源…...

Docker从认识到实践再到底层原理(九)|Docker Compose 容器编排
前言 那么这里博主先安利一些干货满满的专栏了! 首先是博主的高质量博客的汇总,这个专栏里面的博客,都是博主最最用心写的一部分,干货满满,希望对大家有帮助。 高质量博客汇总 然后就是博主最近最花时间的一个专栏…...

操作EXCEL计算3万条数据的NDVI并填入
Python操作EXCEL,计算3万条数据的NDVI并填入 问题描述 现在是有构建好了的查找表,不过构建了3万条数据,在excel中手动计算每行的NDVI值太麻烦了,也不会操作。 就试试python吧,毕竟python自动处理大型EXCEL数据很方便…...
Linux服务器安装Anaconda 配置远程jupyter lab使用虚拟环境
参考的博客: Linux服务器安装Anaconda 并配置远程jupyter lab anaconda配置远程访问jupyter,并创建虚拟环境 理解和创建:Anaconda、Jupyterlab、虚拟环境、Kernel 下边是正文了。 https://www.anaconda.com/download是官网网址,可…...
)
R语言实现随机生存森林(3)
常见问题解答 1、计算C指数 1-Error rate,或者 rsf.err <- get.cindex(yvar$Survival_months,yvar$OS,predictedrf.grow$predicted) 2、模型中predicted和predicted.oob区别 predicted和predicted.oob是两个不同的属性,它们分别表示模型的预测结果…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...
