Pytorch中关于forward函数的理解与用法
目录
- 前言
- 1. 问题所示
- 2. 原理分析
- 2.1 forward函数理解
- 2.2 forward函数用法
前言
深入深度学习框架的代码,发现forward函数没有被显示调用
但代码确重写了forward函数,于是好奇是不是python的魔术方法作用
1. 问题所示
代码如下所示:
class Module(nn.Module):# 初始化def __init__(self):super(Module, self).__init__()# ......# 前向传播def forward(self, x):# ......return x# 输入数据
data = ..... # 实例化
module = Module()# 前向传播
module(data)
整个代码串没有显示调用forward函数
由此引发疑问:
- 谁去调用forward函数?
- 什么时候调用forward函数?
2. 原理分析
回顾python的基础知识:python 类和对象的详细分析
可以清楚知道对象需要执行方法,在方法中传入参数即可,类似 module.forward(data),但是执行对象(参数)就可成功。
这也说明:module(data) 等价于 module.forward(data)。
即该代码块调用了forward函数(那他是怎样实现什么时候调用的呢)
本身Pytorch大部分操作都是通过继承nn.Module类实现,查看其源代码:
class Module(object):def __init__(self):def forward(self, *input):def add_module(self, name, module):def cuda(self, device=None):def cpu(self):def __call__(self, *input, **kwargs):def parameters(self, recurse=True):def named_parameters(self, prefix='', recurse=True):def children(self):def named_children(self):def modules(self): def named_modules(self, memo=None, prefix=''):def train(self, mode=True):def eval(self):def zero_grad(self):def __repr__(self):def __dir__(self):
内部中有个def __call__(self, *input, **kwargs):函数,默认父类会执行该函数
大致如下:
class Module():def __call__(self, data): print(data)module = Module()# 输出 1
module(1)
这正说明,深度学习的模型继承了nn.Module类,内部的__call__方法有对forward方法的调用,才不用显式地调用forward方法。
对此,深度学习的模型框架需要重写构造函数中的__init__函数和forward函数。
2.1 forward函数理解
- 通过module中的__call__方法
- __call__方法调用module中的forward方法
- forward方法
—若碰到Module子类,则迭代回馈第一步;
—若碰到Function子类,则执行第四步; - 调用Function子类中的call方法
- __call__方法调用Function中的forward方法
- 由于层层嵌套,现在只需回馈上一层的值即可
( Function中的forward返回值 ->
module中的forward返回值 ->
module中的__call__进行forward_hook返回值)
代码逻辑如下:
def __call__(self, *input, **kwargs):# 此处执行forward函数result = self.forward(*input, **kwargs)for hook in self._forward_hooks.values():#将注册的hook拿出来用hook_result = hook(self, input, result)return result-
围观角度:所谓的__call__为函数调用,只需要将该类型的对象当做函数使用即可,即
module(data)等价于module.forward(data)。 -
宏观角度:当一个类默认实现特殊方法__call__,该类的实例就变成可调用的类型,即
对象名()等价于对象名.__call__()
2.2 forward函数用法
CNN可学习的参数层和不可学习的参数层,大致如下:
- 可学习的参数:卷积层和全连接层的权重、bias、BatchNorm的β和γ等。
- 不可学习的参数(超参数):学习率、batch size、weight decay、模型的深度宽度分辨率等。
- Module类中的init构造函数一般放置可学习的参数,其不可学习的参数如果不放置在init层,则在forward函数中可用nn.functional来代替。
- forward函数必须重写(实现模型功能,链接各层之间的功能)
相关文章:

Pytorch中关于forward函数的理解与用法
目录 前言1. 问题所示2. 原理分析2.1 forward函数理解2.2 forward函数用法 前言 深入深度学习框架的代码,发现forward函数没有被显示调用 但代码确重写了forward函数,于是好奇是不是python的魔术方法作用 1. 问题所示 代码如下所示: cla…...
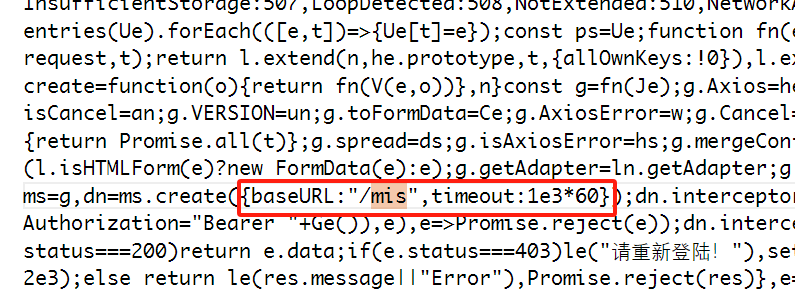
vite跨域proxy设置与开发、生产环境的接口配置,接口在生产环境下,还能使用proxy代理地址吗
文章目录 vite的proxy开发环境设置如果后端没有提供可以替换的/mis等可替换的后缀的处理办法接口如何区分.env.development开发和.env.production生产环境接口在生产环境下,还能使用proxy代理地址吗? vite的proxy开发环境设置 环境: vite 4…...
【嵌入式】使用MultiButton开源库驱动按键并控制多级界面切换
目录 一 背景说明 二 参考资料 三 MultiButton开源库移植 四 设计实现--驱动按键 五 设计实现--界面处理 一 背景说明 需要做一个通过不同按键控制多级界面切换以及界面动作的程序。 查阅相关资料,发现网上大多数的应用都比较繁琐,且对于多级界面的…...

【数据结构】树的概念理解和性质推导(保姆级详解,小白必看系列)
目录 一、前言 🍎 为什么要学习非线性结构 ---- 树(Tree) 💦 线性结构的优缺点 💦 优化方案 ----- 树(Tree) 💦 树的讲解流程 二、树的概念及结构 🍐 树的概念 &…...
融合之力:数字孪生、人工智能和数据分析的创新驱动
数字孪生、人工智能(AI)和数据分析是当今科技领域中的三个重要概念,它们之间存在着紧密的关联和互动,共同推动了许多领域的创新和发展。 一、概念 数字孪生是一种数字化的模拟技术,它通过复制现实世界中的物理实体、…...

Spring的注解开发-Spring配置类的开发
Bean配置类的注解开发 Component等注解替代了<bean>标签,但像<import>、<context:componentScan>等非<bean>标签怎样去使用注解去替代呢?定义一个配置类替代原有的xml配置文件,<bean>标签以外的标签ÿ…...
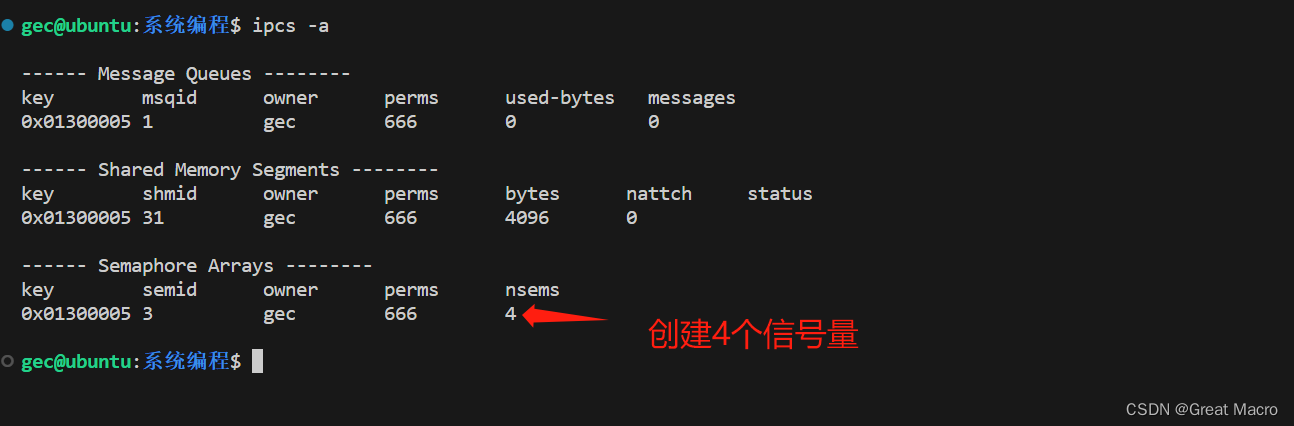
Linux系统编程系列之进程间通信-信号量组
一、什么是信号量组 信号量组是信号量的一种, 是system-V三种IPC对象之一,是进程间通信的一种方式。 二、信号量组的特性 信号量组不是用来传输数据的,而是作为“旗语”,用来协调各进程或者线程工作的。信号量组可以一次性在其内…...

centos 6使用yum安装软件
1. 执行以下命令,查看当前操作系统 CentOS 版本。 cat /etc/centos-release返回结果如下图所示,则说明当前操作系统版本为 CentOS 6.9。 2. 执行以下命令,编辑 CentOS-Base.repo 和CentOS-Epel.repo文件。 vim /etc/yum.repos.d/CentOS-Bas…...
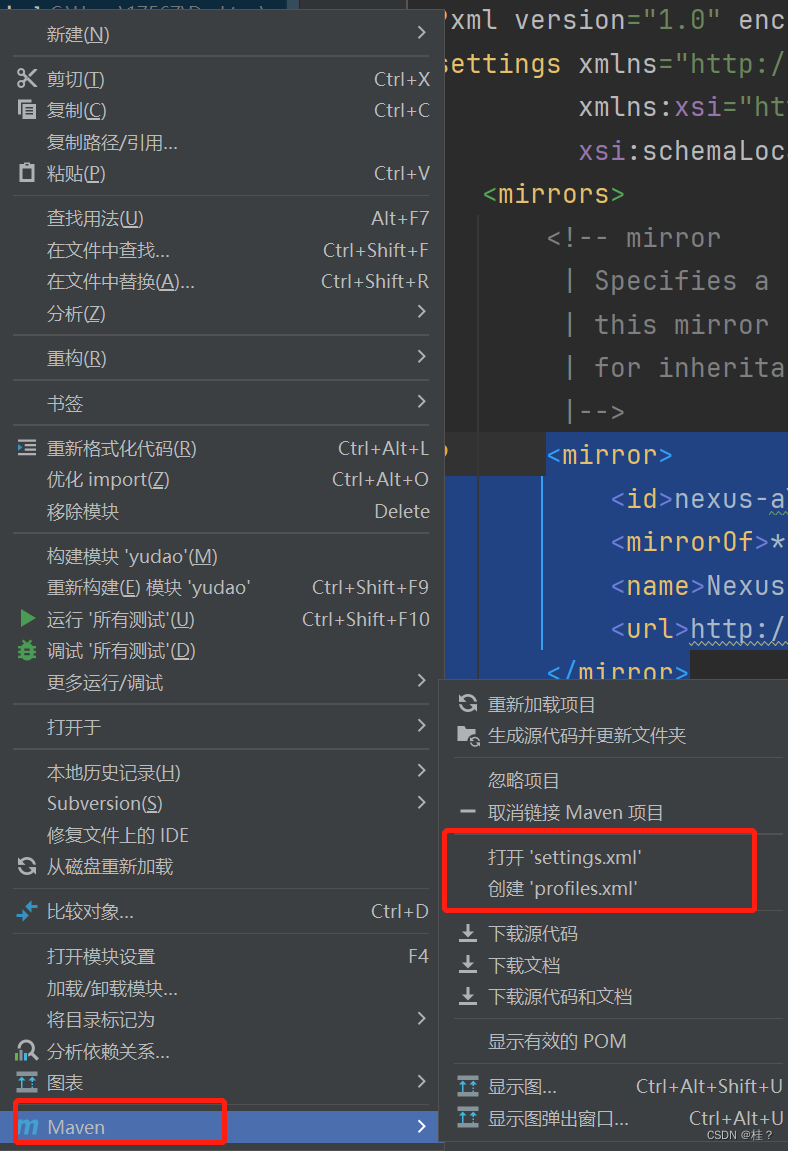
maven无法下载时的解决方法——笔记
右键项目然后点击创建setting.xml(因为现在创建了,所以没显示了,可以直接点击打开setting.xml) 然后添加 <mirror><id>nexus-aliyun</id><mirrorOf>*,!jeecg,!jeecg-snapshots</mirrorOf><name…...

Java Spring Boot 开发框架
Spring Boot是一种基于Java编程语言的开发框架,它的目标是简化Java应用程序的开发过程。Spring Boot提供了一种快速、易于使用的方式来创建独立的、生产级别的Java应用程序。本文将介绍Spring Boot的特性、优势以及如何使用它来开发高效、可靠的应用程序。 一、简介…...

Pytorch学习记录-1-张量
1. 张量 (Tensor): 数学中指的是多维数组; torch.Tensor data: 被封装的 Tensor dtype: 张量的数据类型 shape: 张量的形状 device: 张量所在的设备,GPU/CPU requires_grad: 指示是否需要计算梯度 grad: data 的梯度 grad_fn: 创建 Tensor 的 Functio…...
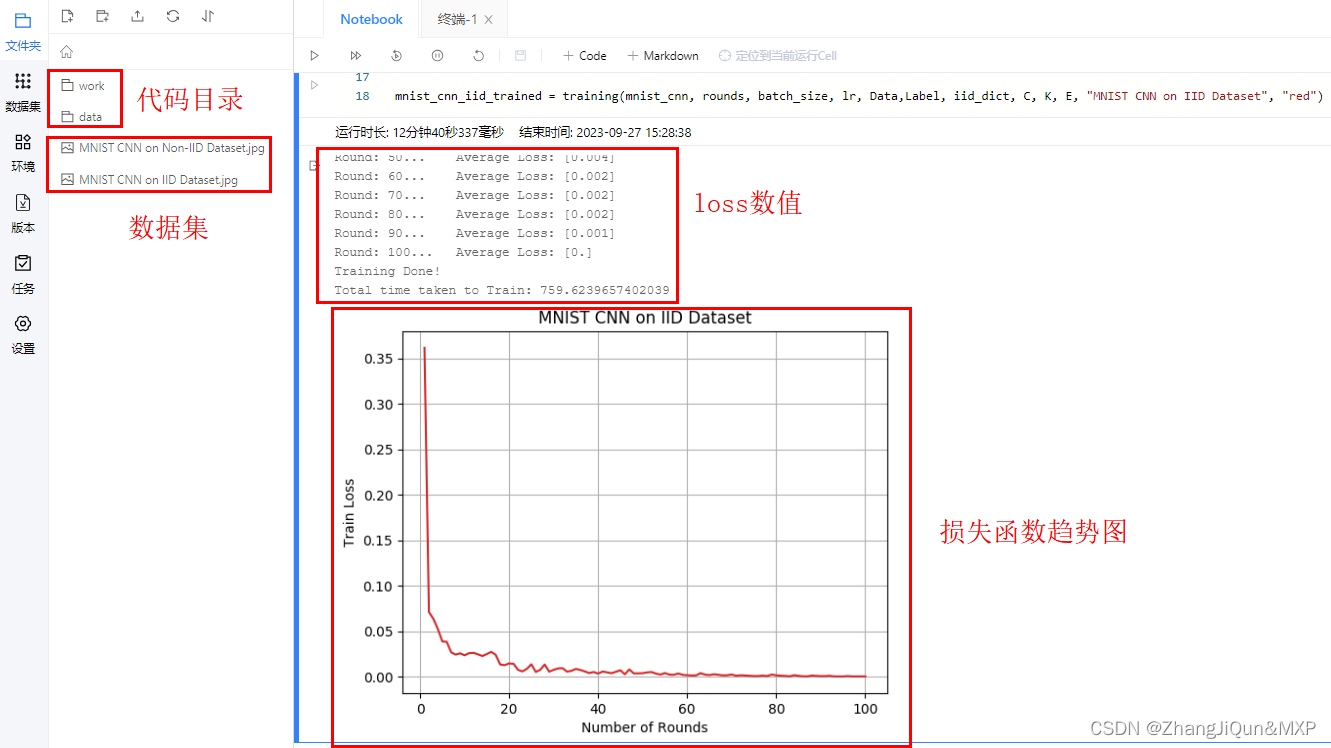
paddle2.3-基于联邦学习实现FedAVg算法-CNN
目录 1. 联邦学习介绍 2. 实验流程 3. 数据加载 4. 模型构建 5. 数据采样函数 6. 模型训练 1. 联邦学习介绍 联邦学习是一种分布式机器学习方法,中心节点为server(服务器),各分支节点为本地的client(设备&#…...

nuiapp保存canvas绘图
要保存一个 Canvas 绘图,可以使用以下步骤: 获取 Canvas 元素和其绘图上下文: var canvas document.getElementById("myCanvas"); var ctx canvas.getContext("2d");使用 Canvas 绘图 API 绘制图形。 使用 toDataUR…...
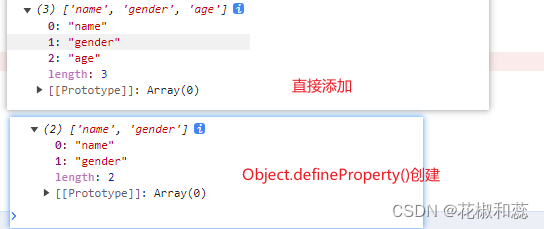
Object.defineProperty()方法详解,了解vue2的数据代理
假期第一篇,对于基础的知识点,我感觉自己还是很薄弱的。 趁着假期,再去复习一遍 Object.defineProperty(),对于这个方法,更多的还是停留在面试的时候,面试官问你vue2和vue3区别的时候,不免要提一提这个方法…...

Linux 磁盘管理
Linux 系统的磁盘管理直接关系到整个系统的性能表现。磁盘管理常用三个命令为: df、du 和 fdisk。 df df(英文全称:disk free)。df 命令用于显示磁盘空间的使用情况,包括文件系统的挂载点、总容量、已用空间、可用空间…...

大数据与人工智能的未来已来
大数据与人工智能的定义 大数据: 大数据指的是规模庞大、复杂性高、多样性丰富的数据集合。这些数据通常无法通过传统的数据库管理工具来捕获、存储、管理和处理。大数据的特点包括"3V": 大量(Volume):大数…...

【AI视野·今日Robot 机器人论文速览 第四十一期】Tue, 26 Sep 2023
AI视野今日CS.Robotics 机器人学论文速览 Tue, 26 Sep 2023 Totally 73 papers 👉上期速览✈更多精彩请移步主页 Daily Robotics Papers Extreme Parkour with Legged Robots Authors Xuxin Cheng, Kexin Shi, Ananye Agarwal, Deepak Pathak人类可以通过以高度动态…...
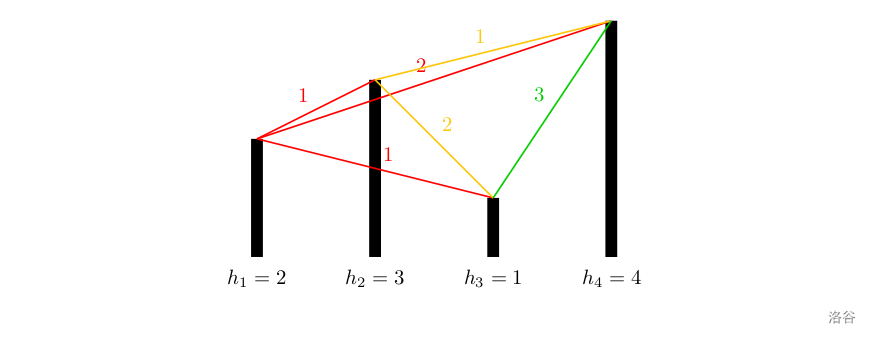
[NOIP2012 提高组] 开车旅行
[NOIP2012 提高组] 开车旅行 题目描述 小 A \text{A} A 和小 B \text{B} B 决定利用假期外出旅行,他们将想去的城市从 $1 $ 到 n n n 编号,且编号较小的城市在编号较大的城市的西边,已知各个城市的海拔高度互不相同,记城市 …...

数据库设计流程---以案例熟悉
案例名字:宠物商店系统 课程来源:点击跳转 信息->概念模型->数据模型->数据库结构模型 将现实世界中的信息转换为信息世界的概念模型(E-R模型) 业务逻辑 构建 E-R 图 确定三个实体:用户、商品、订单...
Miniconda创建paddlepaddle环境
1、conda env list 2、conda create --name paddle_env python3.8 --channel https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/free/ 3、activate paddle_env 4、python -m pip install paddlepaddle -i https://mirror.baidu.com/pypi/simple 5、pip install "p…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...
