【考研数学】概率论与数理统计 —— 第三章 | 二维随机变量及其分布(1,二维连续型和离散型随机变量基本概念与性质)
文章目录
- 引言
- 一、二维随机变量及分布
- 1.1 基本概念
- 1.2 联合分布函数的性质
- 二、二维离散型随机变量及分布
- 三、多维连续型随机变量及分布
- 3.1 基本概念
- 3.2 二维连续型随机变量的性质
- 写在最后
引言
隔了好长时间没看概率论了,上一篇文章还是 8.29 ,快一个月了。主要是想着高数做到多元微分和二重积分题目,再来看这个概率论二维的来,更好理解。不过没想到内容太多了,到现在也只到二元微分的进度。
一、二维随机变量及分布
1.1 基本概念
定义 1 —— 二维随机变量。设 X , Y X,Y X,Y 为定义于同一样本空间上的两个随机变量,称 ( X , Y ) (X,Y) (X,Y) 为二维随机变量。同理,也有 n n n 维随机变量的定义。
定义 2 —— 二维随机变量的分布函数。
(1)设 ( X , Y ) (X,Y) (X,Y) 为二维随机变量,对任意的 x , y ∈ R x,y\in R x,y∈R ,称 F ( x , y ) = P { X ≤ x , Y ≤ y } F(x,y)=P\{X\leq x,Y\leq y\} F(x,y)=P{X≤x,Y≤y} 为二维随机变量 ( X , Y ) (X,Y) (X,Y) 的联合分布函数。
(2)称函数 F X ( x ) = P { X ≤ x } , F Y ( y ) = P { Y ≤ y } F_X(x)=P\{X\leq x\},F_Y(y)=P\{Y\leq y\} FX(x)=P{X≤x},FY(y)=P{Y≤y} 分别为随机变量 X , Y X,Y X,Y 的边缘分布函数。同理,有 n n n 维随机变量的联合分布函数以及边缘分布函数。
1.2 联合分布函数的性质
设 ( X , Y ) (X,Y) (X,Y) 为二维随机变量, F ( x , y ) F(x,y) F(x,y) 为其联合分布函数,有如下性质:
(1) 0 ≤ F ( x , y ) ≤ 1 ; 0 \leq F(x,y) \leq 1; 0≤F(x,y)≤1;
(2) F ( x , y ) F(x,y) F(x,y) 对 x , y x,y x,y 都是单调不减函数;
(3) F ( x ) F(x) F(x) 关于 x , y x,y x,y 都是右连续;
(4) F ( − ∞ , − ∞ ) = 0 = F ( − ∞ , + ∞ ) = F ( + ∞ , − ∞ ) = 0 , F ( + ∞ , + ∞ ) = 1. F(-\infty,-\infty)=0=F(-\infty,+\infty)=F(+\infty,-\infty)=0,F(+\infty,+\infty)=1. F(−∞,−∞)=0=F(−∞,+∞)=F(+∞,−∞)=0,F(+∞,+∞)=1.
其实和一维随机变量的分布函数的性质大差不差的,我也是从一维那里复制过来改了下的hhh。
以下是一些推论:
(1)设 { X ≤ x } = A , { Y ≤ y } = B \{X\leq x\}=A,\{Y\leq y\}=B {X≤x}=A,{Y≤y}=B ,则 F ( x , y ) = P ( A B ) , F X ( x ) = P ( A ) , F Y ( y ) = P ( B ) . F(x,y)=P(AB),F_X(x)=P(A),F_Y(y)=P(B). F(x,y)=P(AB),FX(x)=P(A),FY(y)=P(B). 即联合分布函数是要取交集。
(2) F X ( x ) = F ( x , + ∞ ) , F Y ( y ) = F ( + ∞ , y ) . F_X(x)=F(x,+\infty),F_Y(y)=F(+\infty,y). FX(x)=F(x,+∞),FY(y)=F(+∞,y). 即当一个变量限制在小于正无穷范围(这是肯定的),当然此时联合分布函数和边缘分布函数一致了。
(3)设 a 1 < a 2 , b 1 < b 2 a_1<a_2,b_1<b_2 a1<a2,b1<b2 ,则
P { a 1 < X ≤ a 2 , b 1 < Y ≤ b 2 } = P { a 1 < X ≤ a 2 , Y ≤ b 2 } − P { a 1 < X ≤ a 2 , Y ≤ b 1 } = ( P { X ≤ a 2 , Y ≤ b 2 } − P { X ≤ a 1 , Y ≤ b 2 } ) − ( P { X ≤ a 2 , Y ≤ b 1 } − P { X ≤ a 1 , Y ≤ b 1 } ) = F ( a 2 , b 2 ) − F ( a 1 , b 2 ) − F ( a 2 , b 1 ) + F ( a 1 , b 1 ) . P\{a_1 < X\leq a_2,b_1 < Y \leq b_2\}=P\{a_1 < X\leq a_2,Y\leq b_2\}-P\{a_1 < X\leq a_2,Y \leq b_1\}=(P\{X \leq a_2,Y\leq b_2\}-P\{X \leq a_1,Y\leq b_2\})-(P\{X \leq a_2,Y\leq b_1\}-P\{X\leq a_1,Y\leq b_1\})=\pmb{F(a_2,b_2)-F(a_1,b_2)-F(a_2,b_1)+F(a_1,b_1)}. P{a1<X≤a2,b1<Y≤b2}=P{a1<X≤a2,Y≤b2}−P{a1<X≤a2,Y≤b1}=(P{X≤a2,Y≤b2}−P{X≤a1,Y≤b2})−(P{X≤a2,Y≤b1}−P{X≤a1,Y≤b1})=F(a2,b2)−F(a1,b2)−F(a2,b1)+F(a1,b1).
二、二维离散型随机变量及分布
设 ( X , Y ) (X,Y) (X,Y) 为二维随机变量,若 ( X , Y ) (X,Y) (X,Y) 的可能取值为有限对或可列对,称 ( X , Y ) (X,Y) (X,Y) 为二维离散型随机变量。
设随机变量 ( X , Y ) (X,Y) (X,Y) 的可能取值为 ( x i , y j ) ( i = 1 , 2 , ⋯ , m ; j = 1 , 2 , ⋯ , n ) (x_i,y_j)(i=1,2,\cdots,m;j=1,2,\cdots,n) (xi,yj)(i=1,2,⋯,m;j=1,2,⋯,n) ,称 P { X ≤ x i , Y ≤ y j } = p i j ( i = 1 , 2 , ⋯ , m ; j = 1 , 2 , ⋯ , n ) , 或 P\{X\leq x_i,Y\leq y_j\}=p_{ij}(i=1,2,\cdots,m;j=1,2,\cdots,n),或 P{X≤xi,Y≤yj}=pij(i=1,2,⋯,m;j=1,2,⋯,n),或
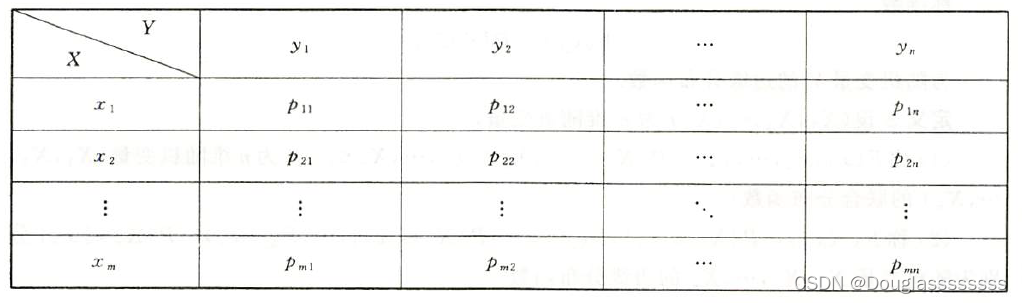
为 ( X , Y ) (X,Y) (X,Y) 的联合分布律。其具有如下性质:
- p i j ≥ 0 ( i = 1 , 2 , ⋯ , m ; j = 1 , 2 , ⋯ , n ) ; p_{ij}\geq 0(i=1,2,\cdots,m;j=1,2,\cdots,n); pij≥0(i=1,2,⋯,m;j=1,2,⋯,n);
- ∑ ∑ p i j = 1. \sum\sum p_{ij}=1. ∑∑pij=1.
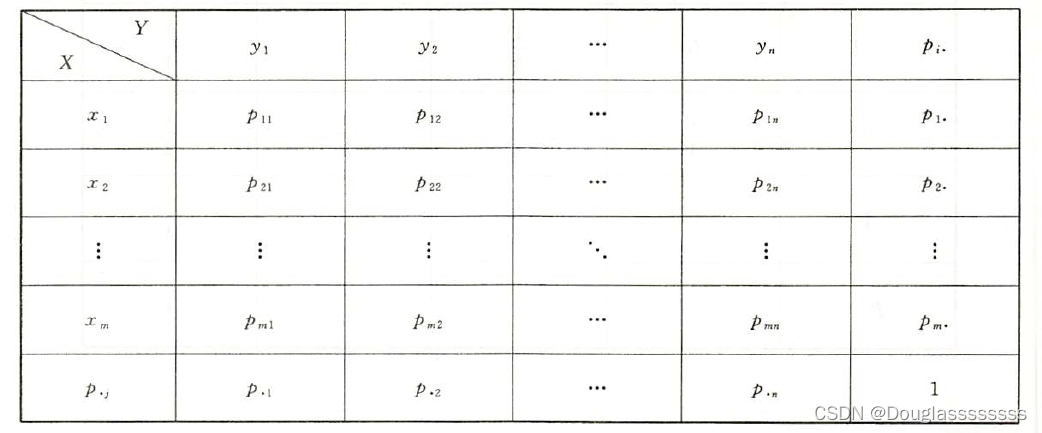
由全概率公式,有 P { X = x i } = P { X = x i , y 1 } + ⋯ + P { X = x i , y n } = p i 1 + ⋯ + p i , n = p i ( i = 1 , 2 , ⋯ , m ) . P\{X=x_i\}=P\{X=x_i,y_1\}+\cdots+P\{X=x_i,y_n\}=p_{i1}+\cdots+p_{i,n}=p_i(i=1,2,\cdots,m). P{X=xi}=P{X=xi,y1}+⋯+P{X=xi,yn}=pi1+⋯+pi,n=pi(i=1,2,⋯,m). 同理,可以得到 P { Y = y i } P\{Y= y_i\} P{Y=yi} 。于是,联合分布律每一行每一列之和,即可构成两个随机变量的边缘分布律。

一般情况下,联合分布律和边缘分布律可以放在一张表格中:
三、多维连续型随机变量及分布
3.1 基本概念
设 ( X , Y ) (X,Y) (X,Y) 为二维随机变量,其分布函数为 F ( x , y ) = P { X ≤ x , Y ≤ y } F(x,y)=P\{X\leq x,Y\leq y\} F(x,y)=P{X≤x,Y≤y} ,若存在非负可积函数 f ( x , y ) f(x,y) f(x,y) ,使得 F ( x , y ) = ∫ − ∞ x d u ∫ − ∞ y f ( u , v ) d v F(x,y)=\int_{-\infty}^xdu\int_{-\infty}^yf(u,v)dv F(x,y)=∫−∞xdu∫−∞yf(u,v)dv ,称 ( X , Y ) (X,Y) (X,Y) 为二维连续型随机变量, f ( x , y ) f(x,y) f(x,y) 为 ( X , Y ) (X,Y) (X,Y) 的联合密度函数, F ( x , y ) F(x,y) F(x,y) 为联合分布函数。
称 f X ( x ) = ∫ − ∞ ∞ f ( x , y ) d y , f Y ( y ) = ∫ − ∞ ∞ f ( x , y ) d x f_X(x)=\int_{-\infty}^\infty f(x,y)dy,f_Y(y)=\int_{-\infty}^\infty f(x,y)dx fX(x)=∫−∞∞f(x,y)dy,fY(y)=∫−∞∞f(x,y)dx 分别为随机变量 X , Y X,Y X,Y 的边缘密度函数。
称 F X ( x ) = ∫ − ∞ x f X ( x ) d x , F Y ( y ) = ∫ − ∞ y f Y ( y ) d y F_X(x)=\int_{-\infty}^xf_X(x)dx,F_Y(y)=\int_{-\infty}^yf_Y(y)dy FX(x)=∫−∞xfX(x)dx,FY(y)=∫−∞yfY(y)dy 分别为随机变量 X , Y X,Y X,Y 的边缘分布函数。
同理,以上结论可推广到 n n n 维。
3.2 二维连续型随机变量的性质
设 f ( x , y ) f(x,y) f(x,y) 为二维随机变量 ( X , Y ) (X,Y) (X,Y) 的联合密度函数,则
- f ( x , y ) ≥ 0 ; f(x,y)\geq 0; f(x,y)≥0;
- ∫ − ∞ ∞ d x ∫ − ∞ ∞ f ( x , y ) d y = 1. \int_{-\infty}^\infty dx\int_{-\infty}^\infty f(x,y)dy=1. ∫−∞∞dx∫−∞∞f(x,y)dy=1.
设 ( X , Y ) (X,Y) (X,Y) 为二维连续型随机变量, f ( x , y ) f(x,y) f(x,y) 为其联合密度函数, F ( x , y ) F(x,y) F(x,y) 为其联合分布函数。若 F ( x , y ) F(x,y) F(x,y) 在某点 ( x , y ) (x,y) (x,y) 处二阶可偏导,有 f ( x , y ) = ∂ F ∂ x ∂ y ; f(x,y)=\frac{\partial F}{\partial x \partial y}; f(x,y)=∂x∂y∂F; 若在某点处二阶不可偏导,则 f ( x , y ) = 0 f(x,y)=0 f(x,y)=0 。
二阶联合分布函数一定连续,但不一定二阶可偏导。
写在最后
果然,先去看看多元微分和多重积分,看这个就较为轻松。
相关文章:

【考研数学】概率论与数理统计 —— 第三章 | 二维随机变量及其分布(1,二维连续型和离散型随机变量基本概念与性质)
文章目录 引言一、二维随机变量及分布1.1 基本概念1.2 联合分布函数的性质 二、二维离散型随机变量及分布三、多维连续型随机变量及分布3.1 基本概念3.2 二维连续型随机变量的性质 写在最后 引言 隔了好长时间没看概率论了,上一篇文章还是 8.29 ,快一个…...

cesium 雷达扫描 (波纹线性雷达扫描效果)
cesium 雷达扫描 (波纹线性雷达扫描效果) 1、实现方法 使用ellipse方法加载圆型,修改ellipse中material方法来实现效果 2、示例代码 2.1 <!DOCTYPE html> <html lang="en"><head>&l...

SLAM从入门到精通(tf的使用)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 在ros的机器人学习过程中,有一件事情是肯定少不了的。那就是坐标系的转换。其实这也很容易理解。假设有一个机器人,它有一个…...
python代码混淆与代码打包
0x00 背景 自己写的项目,又想保护源码,自己做个混淆是最方便的了。 0x01 实践 这里使用开源工具 GitHub - astrand/pyobfuscate: pyobfuscate,虽然git上才500多star,但是很好用。它的使用场景是混淆单个py文件。很多事物有开始就…...
)
Codeforces Round 899 (Div. 2)
Dashboard - Codeforces Round 899 (Div. 2) - Codeforces A. Increasing Sequence 由于a与b不相等,但b必须算出最小故可以从最小开始(1),故如果b a就将其值,使其改变即可,其余由于b1 < b2 < b3..…...

【 SuperPoint 】图像特征提取上的对比实验
1. SIFT,SuperPoint 都具有提取图片特征点,并且输出特征描述子的特性,本篇文章从特征点的提取数量,特征点的正确匹配数量来探索一下二者的优劣。 SuperPoint提取到的特征点数量要少一些,可以理解,我想原因大…...
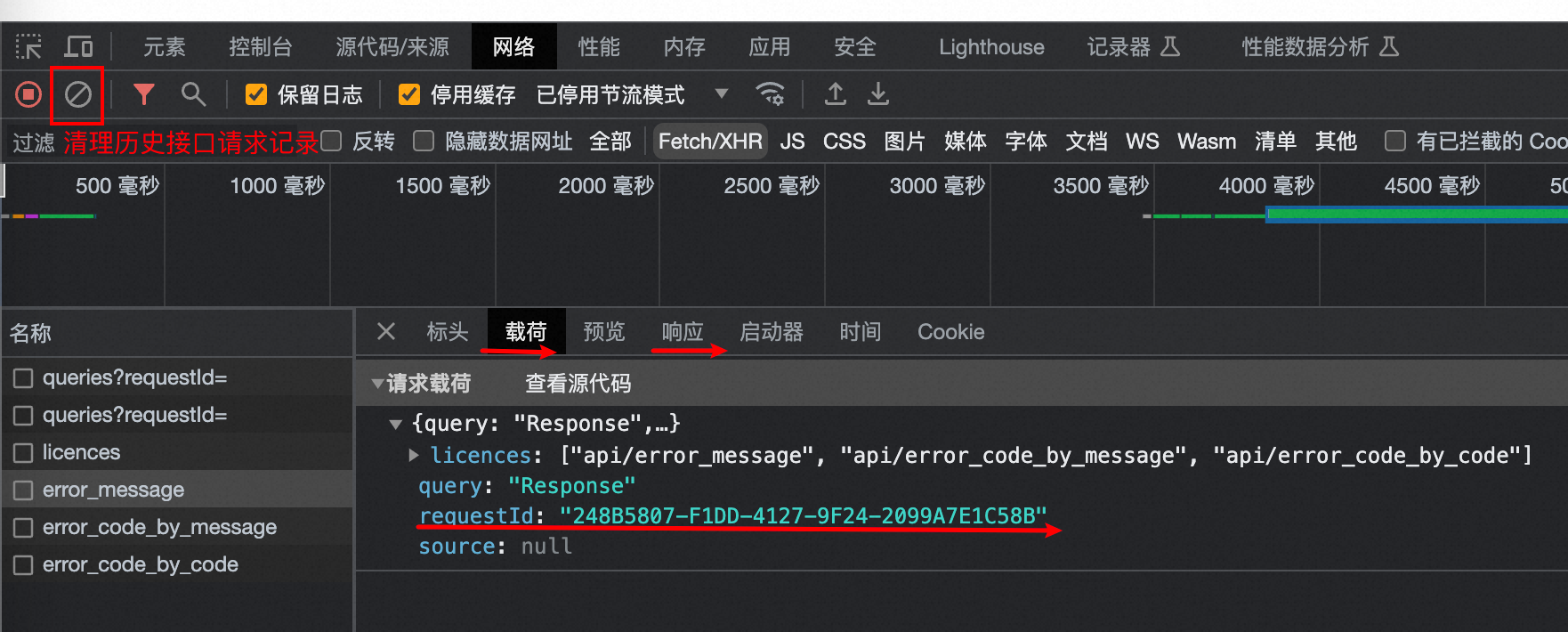
Chrome获取RequestId
Chrome获取RequestId 参考:https://help.aliyun.com/zh/redis/how-do-i-obtain-the-id-of-a-request 在浏览器页面按下F12键,打开开发者工具页面; 在开发者工具页面,单击Network(网络); 在playload(载荷)窗口中找到目…...

cesium 雷达扫描 (线行扩散效果)
cesium 雷达扫描 (线行扩散效果) 1、实现方法 使用ellipse方法加载圆型,修改ellipse中material方法来实现效果 2、示例代码 2.1、 <!DOCTYPE html> <html lang="en"><head><<...
【React】React组件生命周期以及触发顺序(部分与vue做比较)
最近在学习React,发现其中的生命周期跟Vue有一些共同点,但也有比较明显的区别,并且执行顺序也值得讨论一下,于是总结了一些资料在这里,作为学习记录。 v17.0.1后生命周期图片 初始化阶段 由ReactDOM.render()触发 —…...

【C++】多线程的学习笔记——白话文版(bushi
目录 为什么要使用多线程 例子 代码 结果 首先要先学的库——thread库 thread的简介 thread的具体使用方法 基本变量的定义 注意(小重点) join函数的解读(重点) detach函数的解读 注意 关于vector和thread是联合使用 …...
图像处理: ImageKit.NET 3.0.10704 Crack
关于 ImageKit.NET3 100% 原生 .NET 图像处理组件。 ImageKit.NET 可让您快速轻松地向 .NET 应用程序添加图像处理功能。从 TWAIN 扫描仪和数码相机检索图像;加载和保存多种格式的图像文件;对图像应用图像滤镜和变换;在显示屏、平移窗口或缩略…...
K8S内容分发网络之集群,nginx,负载均衡,防火墙
K8S内容分发网络之集群,nginx,负载均衡,防火墙 一、Kubernetes 区域可采用 Kubeadm 方式进行安装。1.所有节点,关闭防火墙规则,关闭selinux,关闭swap交换2.修改主机名3.所有节点修改hosts文件4.调整内核参数…...
不愧是疑问解决神器!你强任你强
不愧是疑问解决神器!你强任你强👍👍👍 在过去,我习惯用这种方式来阅读书籍或文章:先快速浏览一遍,然后再进行复读,并最终总结所学的知识点。然而,长期以来,我…...
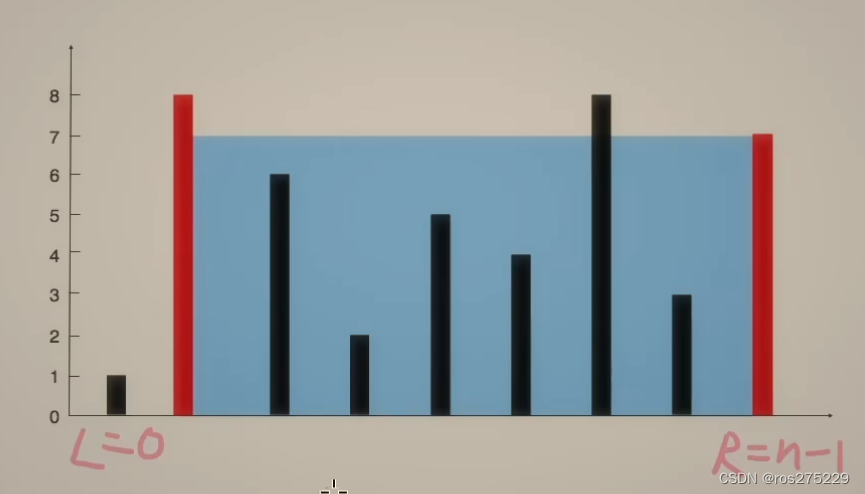
盛最多水的容器 接雨水【基础算法精讲 02】
盛雨水最多的容器 链接 : 11 盛最多水的容器 思路 : 双指针 : 1.对于两条确定的边界,l和r,取中间的线m与r组成容器,如果m的高度>l的高度,那么整个容器的长度会减小,如果低于l的高度,那么不仅高度可…...
之—— 主题的functions.php)
WordPress主题开发( 十二)之—— 主题的functions.php
WordPress主题开发( 十)之—— 主题的functions.php 介绍使用functions.php vs. 插件创建和使用functions.php在functions.php中的常见用途1. 使用WordPress钩子2. 启用WordPress功能3. 定义可重用的函数4. 添加自动Feed链接5. 自定义导航菜单6. 文本域加…...

代码的工厂模式
概念: 代码的工厂模式是一种设计模式,用于创建对象实例而无需直接调用构造函数。它提供了一种更加灵活和可维护的方式来创建对象,尤其是在需要根据不同情况创建不同类型的对象时非常有用。工厂模式隐藏了对象的创建细节,使代码更…...
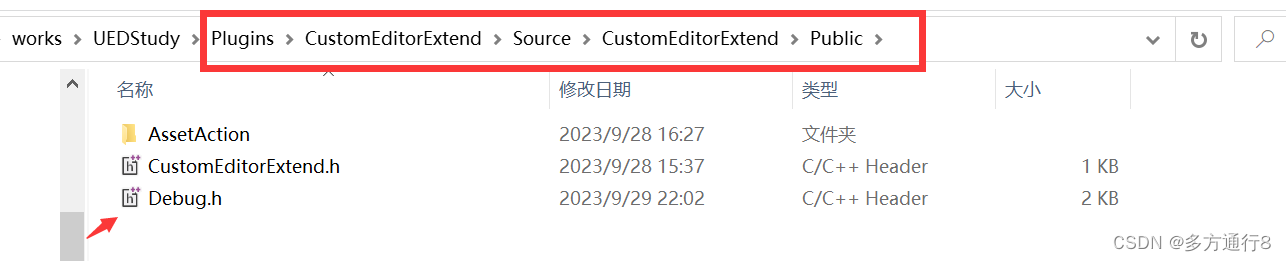
UE5.1编辑器拓展【一、脚本化资产行为,通知,弹窗,高效复制多个同样的资产】
目录 插件制作 添加新的类:AssetActionUtility 添加新的模块:EditorScriptingUtilities 路径了解 添加debug的头文件 代码【debug.h】内涵注释: 写函数 .h文件 .cpp文件 插件制作 首先第一步是做一个插件:…...

mac openssl 版本到底怎么回事 已解决
在mac 安装node多版本的时候,有可能把原有的 openssl1.1 版本 直接要再一次升级了,无奈的 php环境 编译器是 openssl 1.1 还是 3.0 ,今天来个底朝天的找问题。 brew search openssl 有安装 三个版本。 但是错误提示 是第二个版本。 brew …...

AWS】在EC2上创建root用户,并使用root用户登录
最近有项目需要使用AWS的EC2服务器; 在创建服务器实例之后发现,没有root用户,仔细阅读AWS EC2文档,发现默认是ec2-user用户; 那我们需要创建一个root用户 1.创建 root 用户 注意:必须要要在ec2-user用户下…...

9月24日回顾
1.微程序控制器的组成:指令译码器、微地址寄存器(输出和暂存控制信息),时序电路、最核心的部件是控制存储器(只读ROM组成)—用来存储微指令 2.突发读写:比如说突发地址为8,那么只需…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 )
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...
