【LeetCode周赛】LeetCode第365场周赛
目录
- 有序三元组中的最大值 I
- 有序三元组中的最大值 II
- 无限数组的最短子数组
有序三元组中的最大值 I
给你一个下标从 0 开始的整数数组nums。
请你从所有满足 i < j < k 的下标三元组 (i, j, k) 中,找出并返回下标三元组的最大值。如果所有满足条件的三元组的值都是负数,则返回 0 。
下标三元组 (i, j, k) 的值等于 (nums[i] - nums[j]) * nums[k] 。
示例 1:
输入:nums = [12,6,1,2,7]
输出:77
解释:下标三元组 (0, 2, 4) 的值是 (nums[0] -nums[2]) * nums[4] = 77 。 可以证明不存在值大于 77 的有序下标三元组。
示例 2:
输入:nums = [1,10,3,4,19]
输出:133
解释:下标三元组 (1, 2, 4) 的值是 (nums[1] -nums[2]) * nums[4] = 133 。 可以证明不存在值大于 133 的有序下标三元组。
示例 3:
输入:nums = [1,2,3]
输出:0
解释:唯一的下标三元组 (0, 1, 2) 的值是一个负数,(nums[0] -nums[1]) * nums[2] = -3 。因此,答案是 0 。
提示:
3 < = n u m s . l e n g t h < = 100 3 <= nums.length <= 100 3<=nums.length<=100
1 < = n u m s [ i ] < = 1 0 6 1 <= nums[i] <= 10^6 1<=nums[i]<=106
分析:
根据数据范围可以发现, n u m s . l e n g t h nums.length nums.length最大也只是100,因此可以直接按照题意,暴力枚举满足题意的 i , j , k i,j,k i,j,k三个位置的数,计算出 ( n u m s [ i ] − n u m s [ j ] ) ∗ n u m s [ k ] (nums[i] - nums[j]) * nums[k] (nums[i]−nums[j])∗nums[k]的值,用ans维护最大值即可。时间复杂度 O ( n 3 ) O(n^3) O(n3)
代码:
class Solution {
public:long long maximumTripletValue(vector<int>& nums) {int n=nums.size();long long ans=0;for(int i=0;i<n;i++){for(int j=i+1;j<n;j++){for(int k=j+1;k<n;k++){ans=max(ans,(long long)(nums[i]-nums[j])*nums[k]);}}}return ans;}
};
有序三元组中的最大值 II
给你一个下标从 0 开始的整数数组nums。
请你从所有满足 i < j < k 的下标三元组 (i, j, k) 中,找出并返回下标三元组的最大值。如果所有满足条件的三元组的值都是负数,则返回 0 。
下标三元组 (i, j, k) 的值等于 (nums[i] - nums[j]) * nums[k] 。
示例 1:
输入:nums = [12,6,1,2,7]
输出:77
解释:下标三元组 (0, 2, 4) 的值是 (nums[0] -nums[2]) * nums[4] = 77 。 可以证明不存在值大于 77 的有序下标三元组。
示例 2:
输入:nums = [1,10,3,4,19]
输出:133
解释:下标三元组 (1, 2, 4) 的值是 (nums[1] -nums[2]) * nums[4] = 133 。 可以证明不存在值大于 133 的有序下标三元组。
示例 3:
输入:nums = [1,2,3]
输出:0
解释:唯一的下标三元组 (0, 1, 2) 的值是一个负数,(nums[0] -nums[1]) * nums[2] = -3 。因此,答案是 0 。
提示:
3 < = n u m s . l e n g t h < = 1 0 5 3 <= nums.length <= 10^5 3<=nums.length<=105
1 < = n u m s [ i ] < = 1 0 6 1 <= nums[i] <= 10^6 1<=nums[i]<=106
分析:
此题为有序三元组中的最大值I的加强版,即数据范围变大了,不可以在使用暴力 O ( n 3 ) O(n^3) O(n3)的方法完成。我们只能在 O ( n ) O(n) O(n)的时间复杂度下完成此题。
不难发现,要使得这个有序下标三元组最大,对于 j j j位置的数来说, i i i和 k k k位置的数都是越大越好,发现了这一点,后续就好处理了。只需要维护每一个 j j j位置的前缀最大值 p r e [ j ] pre[j] pre[j]和后缀最大值 s u f [ j ] suf[j] suf[j],以当前 j j j位置作为下标三元组中间位置的最大值即为 ( p r e [ j ] − n u m s [ j ] ) ∗ s u f [ j ] (pre[j]-nums[j])*suf[j] (pre[j]−nums[j])∗suf[j]。即可在线性时间复杂度内完成该题目。
代码:
class Solution {
public:long long maximumTripletValue(vector<int>& nums) {//记录数组前面和后面的最大数int n=nums.size();vector<int>pre(n+1),suf(n+1);int ma=0;for(int i=0;i<n;i++){pre[i]=ma;ma=max(ma,nums[i]);}ma=0;for(int i=n-1;i>=0;i--){suf[i]=ma;ma=max(ma,nums[i]);}long long ans=0;for(int i=1;i<n-1;i++){//枚举中间的那个数字ans=max((long long)(pre[i]-nums[i])*suf[i],ans);}return ans;}
};
无限数组的最短子数组
给你一个下标从 0 开始的数组 nums 和一个整数 target 。
下标从 0 开始的数组 infinite_nums 是通过无限地将 nums 的元素追加到自己之后生成的。
请你从 infinite_nums 中找出满足 元素和 等于 target 的 最短 子数组,并返回该子数组的长度。如果不存在满足条件的子数组,返回 -1 。
示例 1:
输入:nums = [1,2,3], target = 5
输出:2
解释:在这个例子中 infinite_nums =[1,2,3,1,2,3,1,2,…] 。 区间 [1,2] 内的子数组的元素和等于 target = 5 ,且长度 length = 2 。 可以证明,当元素和等于目标值 target = 5 时,2 是子数组的最短长度。
示例 2:
输入:nums = [1,1,1,2,3], target = 4
输出:2
解释:在这个例子中 infinite_nums =[1,1,1,2,3,1,1,1,2,3,1,1,…]. 区间 [4,5] 内的子数组的元素和等于 target = 4 ,且长度length = 2 。 可以证明,当元素和等于目标值 target = 4 时,2 是子数组的最短长度。
示例 3:
输入:nums = [2,4,6,8], target = 3
输出:-1
解释:在这个例子中 infinite_nums =[2,4,6,8,2,4,6,8,…] 。 可以证明,不存在元素和等于目标值 target = 3 的子数组。
提示:
1 < = n u m s . l e n g t h < = 1 0 5 1 <= nums.length <= 10^5 1<=nums.length<=105
1 < = n u m s [ i ] < = 1 0 5 1 <= nums[i] <= 10^5 1<=nums[i]<=105
1 < = t a r g e t < = 1 0 9 1 <= target <= 10^9 1<=target<=109
分析:
题目需要计算一个 i n f i n i t e n u m s infinite_nums infinitenums数组中是否能够组成和为 t a r g e t target target的值,我们可以想到,如果 t a r g e t target target能够被构成,则其是被 k k k个 n u n s nuns nuns数组的和 s u m sum sum以及一个余数 v v v构成,即 t a r g e t = k ∗ s u m + v , k > = 0 , 0 < = v < s u m target=k*sum+v,k>=0,0<=v<sum target=k∗sum+v,k>=0,0<=v<sum。
所以我们主要讨论的是 v v v这个数字能否被 i n f i n i t e n u m s infinite_nums infinitenums数组构造出来,因为v是target除以sum的余数,所以 v < s u m v<sum v<sum,因此,如果v能够被构造出来,其肯定是在两个nums数组中的一段数字,且长度不超过n(只用考虑两个nums数组就可以考虑到从nums数组末加到nums数组开头)。
所以可以用双指针来对两个nums数组连接起来的数组进行构造,在右指针移动的同时,一旦当前和total>v,则左指针移动,最终维护一个构造出v值的最短子数组长度。
代码:
class Solution {
public:int minSizeSubarray(vector<int>& nums, int target) {int n=nums.size();long long sum=0;for(int i=0;i<n;i++)sum+=nums[i];int p=target/sum;//至少需要这么多个完整的数组int v=target%sum;//剩下的值,需要从剩下的两个数组中组成int total=0,minn=n;for(int left=0,right=0;right<2*n;right++){total+=nums[right%n];while(total>v)total-=nums[left%n],left++;if(total==v)minn=min(minn,right-left+1);}if(minn==n)return -1;return p*n+minn;}
};
相关文章:

【LeetCode周赛】LeetCode第365场周赛
目录 有序三元组中的最大值 I有序三元组中的最大值 II无限数组的最短子数组 有序三元组中的最大值 I 给你一个下标从 0 开始的整数数组nums。 请你从所有满足 i < j < k 的下标三元组 (i, j, k) 中,找出并返回下标三元组的最大值。如果所有满足条件的三元组的…...
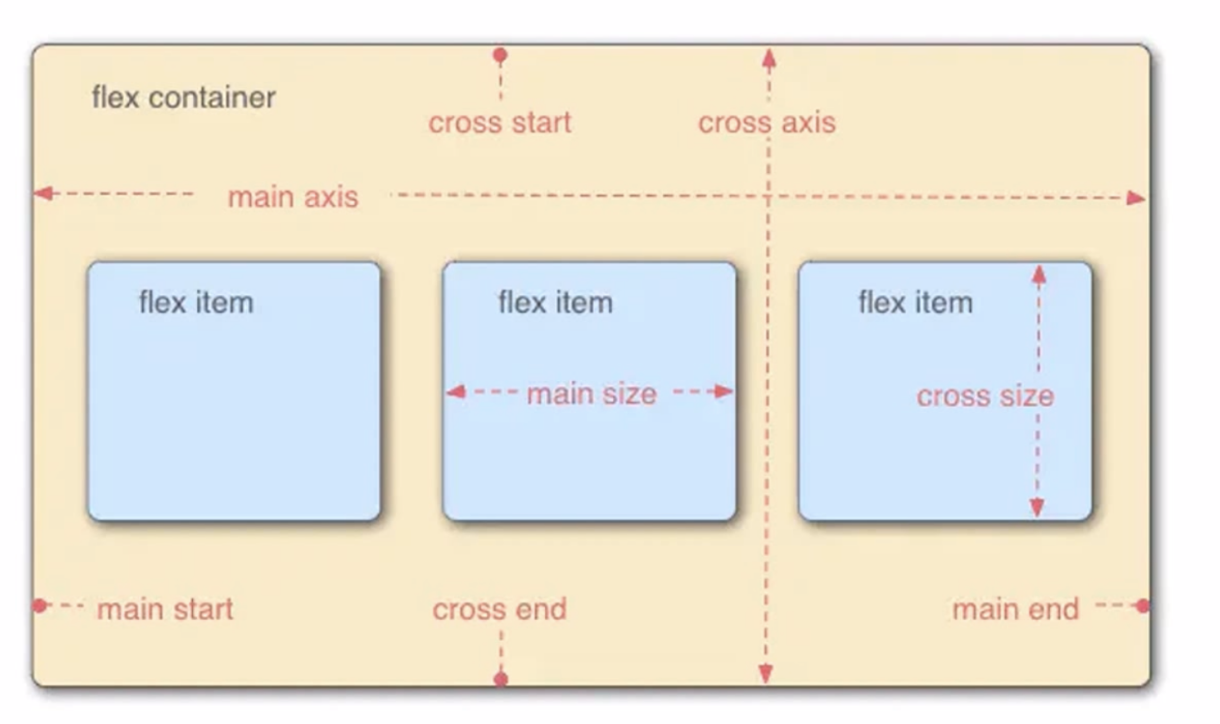
响应式设计的实现方式
一. 什么是响应式 响应式网站设计是一种网络页面设计布局。页面的设计与开发应当根据用户行为以及设备环境(系统平台,屏幕尺寸,屏幕定向等)进行相应的响应和调整。 响应式网站常见特点: 1. 同时适配PC平板手机。 2…...

PHP 反序列化漏洞:__PHP_Incomplete_Class 与 serialize(unserialize($x)) !== $x;
文章目录 参考环境声明__PHP_Incomplete_Class灵显为什么需要 __PHP_Incomplete_Class?不可访问的属性 serialize(unserialize($x)) $x;serialize(unserialize($x)) ! $x;雾现__PHP_Incomplete_Class 对象与其序列化文本的差异试构造 __PHP__Incomplete_Class 对象…...

TempleteMethod
TempleteMethod 动机 在软件构建过程中,对于某一项任务,它常常有稳定的整体操作结构,但各个子步骤却有很多改变的需求,或者由于固有的原因 (比如框架与应用之间的关系)而无法和任务的整体结构同时实现。如…...
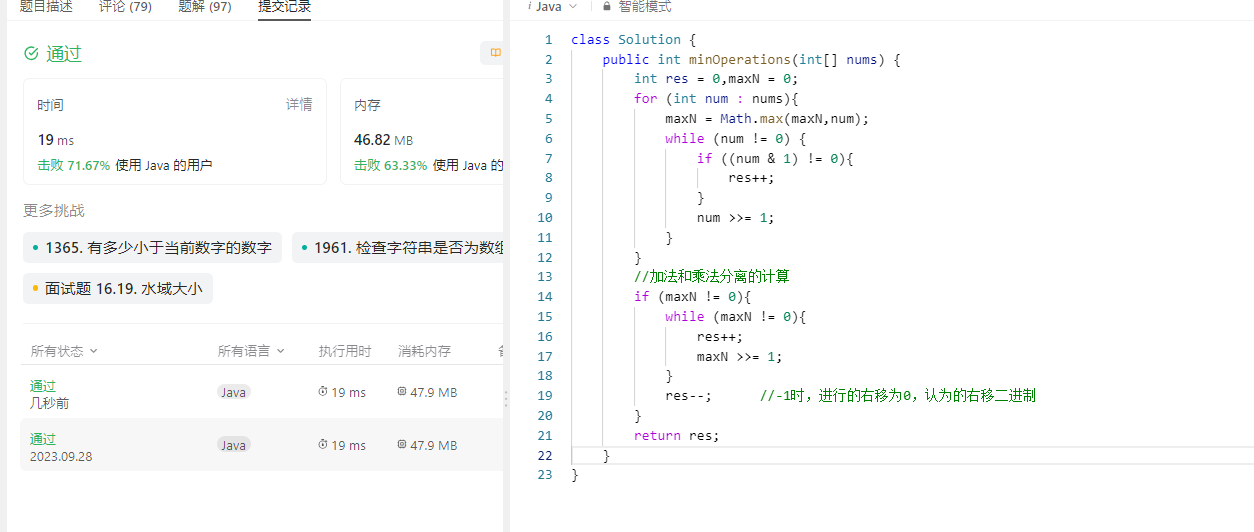
1558. 得到目标数组的最少函数调用次数
1558. 得到目标数组的最少函数调用次数 原题链接:完成情况:解题思路:参考代码: 原题链接: 1558. 得到目标数组的最少函数调用次数 https://leetcode.cn/problems/minimum-numbers-of-function-calls-to-make-target…...

子域名扫描, 后台扫描
子域名和后台扫描 一, 子域名扫描 在渗透测试的早期阶段,子域名扫描是一个非常重要的步骤,它有助于识别目标组织的网络结构和在线资源。 子域名扫描应该在获得适当的权限和授权的情况下进行,以确保所有活动都是合法和合规的。 1. 原因与目…...

毛玻璃带有光影效果的卡片
效果展示 页面结构组成 从效果展示可以看到,页面的主要元素是卡片,卡片的内容呈现上都是比较常规的布局,只是卡片上带有光影效果。 CSS / JavaScript 知识点 transformVanillaTilt.js 使用 页面基础结构实现 <div class"contain…...

【Java】面向过程和面向对象思想||对象和类
1.面向过程和面向对象思想 两者都贯穿于软件分析、设计和开发的各个阶段,对应面向对象就分别称为面向对象的分析(OOA)、面向对象的设计(OOD)和面向对象的编程(OOP)。C语言是一种典型的面向过程语…...
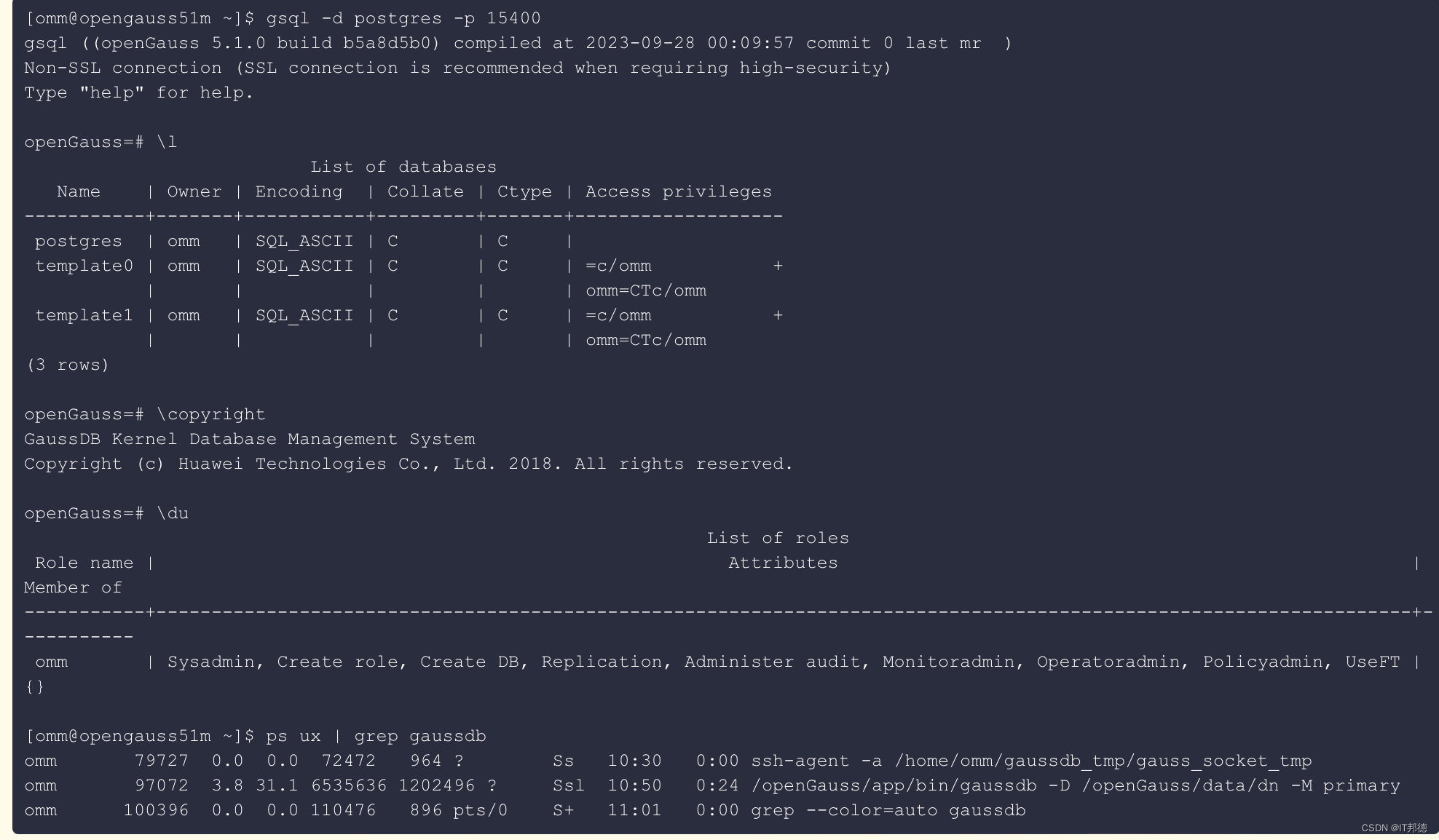
孤举者难起,众行者易趋,openGauss 5.1.0版本正式发布!
📢📢📢📣📣📣 哈喽!大家好,我是【IT邦德】,江湖人称jeames007,10余年DBA及大数据工作经验 一位上进心十足的【大数据领域博主】!😜&am…...
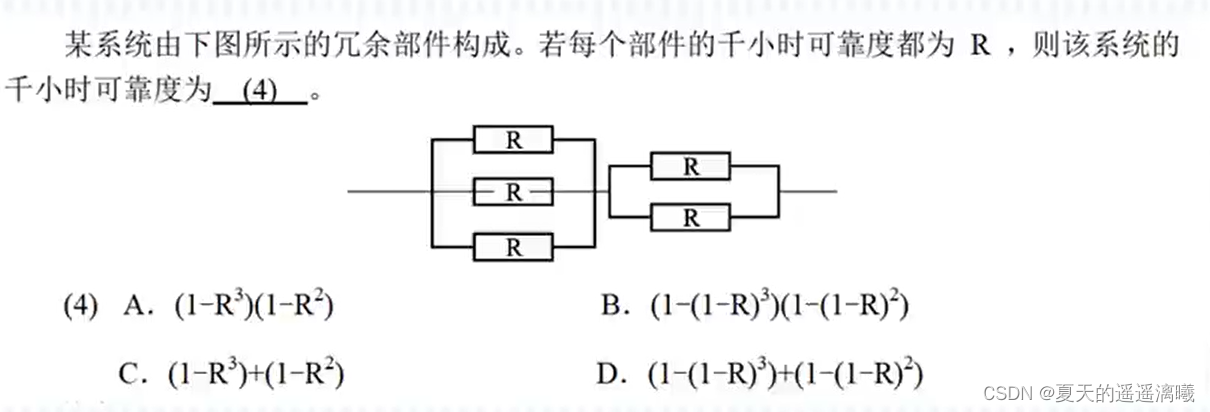
软考——软件设计师中级2023年11月备考(1.计算机组成原理)
一、计算机组成原理 1.数据的表示 1.1 十进制转R进制 方法:对十进制数除R取余,最后对余数取倒序 如: 1.2 原码反码补码 1.3 浮点数 1.4 校验码 —— 海明码 (非重点,了解即可) 海明码的构成方法&…...
前端JavaScript入门到精通,javascript核心进阶ES6语法、API、js高级等基础知识和实战 —— Web APIs(四)
思维导图 一、日期对象 1.1 实例化 实例化,默认得到当前时间,也可以指定时间 1.2 日期对象方法 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible&q…...

【前端】HTML5 Audio 预加载 按照队列顺序播放音频, 可以陆续往队列中加内容
【前端】Audio 按照队列顺序播放音频, 可以陆续往队列中加内容 var 音频库 {} var 当前音频集合 [] /*** 将文本添加到队列中* 持续去播放* 播放过的音频会自动从队列中删除* * 已规划* 要保障同时进行加载的数据不能超过5个(线程池 5)* * param 文本*/播放音频队列(文本){i…...

【单片机】13-实时时钟DS1302
1.RTC的简介 1.什么是实时时钟(RTC) (rtc for real time clock) (1)时间点和时间段的概念区分 (2)单片机为什么需要时间点【一定的时间点干什么事情】 (3)RTC如何存在于…...

springboot和vue:十三、VueX简介与安装与推荐视频+前端数据模拟MockJS
VueX简介与安装与推荐视频 VueX用于管理分散在vue各个组件中的数据。每一个VueX的核心都是一个store,当store中的状态发生变化时,与之绑定的视图也将重新渲染。store中的状态不允许被直接修改,只能显示提交mutationVueX中有五个重要的概念&a…...
[React] Zustand状态管理库
文章目录 1.Zustand介绍2.创建一个store3.使用方法3.1 获取状态3.2 更新状态3.3 访问存储状态3.4 处理异步数据3.5 在状态中访问和存储数组3.6 持续状态 4.总结 1.Zustand介绍 状态管理一直是现代程序应用中的重要组成部分, Zustand使用 hooks 来管理状态无需样板代码。 更少…...

【ChatGPT】ChatGPT发展历史
更多优质文章请看底部:ChatGPT与日本首相交流核废水事件-精准Prompt... hello,我是小索奇,在AI日益庞大的环境下,接下来将为大家不断的ChatGPT学习 ChatGPT使用了 Transformer 结构,建立在 OpenAI的 GPT-3.5 大型语言模…...
分布式文件存储系统Minio实战
分布式文件系统应用场景 互联网海量非结构化数据的存储需求电商网站:海量商品图片视频网站:海量视频文件网盘 : 海量文件社交网站:海量图片 1. Minio介绍 MinIO 是一个基于Apache License v2.0开源协议的对象存储服务。它兼容亚马逊S3云存…...

【MySQL】MySQL 官方安装包形式
MySQL 官方提供3种包: 1. 源码包 mysql-5.7.42.tar.gz mysql-5.7.42-aarch64.tar.gz http://dev.mysql.com/get/Downloads/MySQL-5.6/mysql-5.6.34.tar.gz http://dev.mysql.com/get/Downloads/MySQL-5.7/mysql-5.7.42.tar.gz需要用户根据自己的CPU架构选择对应的…...

使用sqlmap获取数据步骤
文章目录 1.使用sqlmap获取所有数据库2.使用sqlmap获取当前连接数据库3.使用sqlmap获取当前数据库下所有表名4.使用sqlmap获取当前数据库下某个表下所有列名5.使用sqlmap获取当前数据库下某个表下指定字段的数据6.测试当前用户是否是管理员7.使用burpsqlmap批量检测8.脱库命令9…...

[论文笔记]GLM
引言 今天带来论文GLM: General Language Model Pretraining with Autoregressive Blank Infilling的笔记。论文中文标题为 通用语言模型预训练与自回归填空。 有很多不同类型的预训练架构,包括自编码模型(BERT、RoBERTa、ALBERT)、自回归模型(GPT系列)以及编码器-解码器模型…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...
