643. 子数组最大平均数I(滑动窗口)
目录
一、题目
二、代码
一、题目
643. 子数组最大平均数 I - 力扣(LeetCode)

二、代码
class Solution {
public:double findMaxAverage(vector<int>& nums, int k) {double Average = INT_MIN;double sum = nums[0];int left = 0, right = 0;while (right < nums.size()){if (right - left + 1 == k)//满足长度为k{if (sum / (right - left + 1) > Average){Average = sum / (right - left + 1);sum -= nums[left++];}else{if (right + 1 == nums.size()){break;}sum += nums[++right];}}else if (right - left + 1 < k){if (right + 1 == nums.size()){break;}sum += nums[++right];}else//长度大于k,左指针右移{sum -= nums[left++];}}return Average;}
};相关文章:

643. 子数组最大平均数I(滑动窗口)
目录 一、题目 二、代码 一、题目 643. 子数组最大平均数 I - 力扣(LeetCode) 二、代码 class Solution { public:double findMaxAverage(vector<int>& nums, int k) {double Average INT_MIN;double sum nums[0];int left 0, right 0…...

Java 21 新特性:虚拟线程(Virtual Threads)
I often take exercise. Why only yesterday I had breakfast in bed. 在Java 21中,引入了虚拟线程(Virtual Threads)来简化和增强并发性,这使得在Java中编程并发程序更容易、更高效。 虚拟线程,也称为“用户模式线程…...

18scala笔记
Scala2.12 视频地址 1 入门 1.1 发展历史 … 1.2 Scala 和 Java Scala Java 编写代码使用scalac编译成.class字节码文件scala .class文件 执行代码 1.3 特点 1.4 安装 视频地址 注意配置好环境变量 简单代码 1.5 编译文件 编译scala文件会产生两个.class文件 使用java…...

【LeetCode周赛】LeetCode第365场周赛
目录 有序三元组中的最大值 I有序三元组中的最大值 II无限数组的最短子数组 有序三元组中的最大值 I 给你一个下标从 0 开始的整数数组nums。 请你从所有满足 i < j < k 的下标三元组 (i, j, k) 中,找出并返回下标三元组的最大值。如果所有满足条件的三元组的…...
响应式设计的实现方式
一. 什么是响应式 响应式网站设计是一种网络页面设计布局。页面的设计与开发应当根据用户行为以及设备环境(系统平台,屏幕尺寸,屏幕定向等)进行相应的响应和调整。 响应式网站常见特点: 1. 同时适配PC平板手机。 2…...

PHP 反序列化漏洞:__PHP_Incomplete_Class 与 serialize(unserialize($x)) !== $x;
文章目录 参考环境声明__PHP_Incomplete_Class灵显为什么需要 __PHP_Incomplete_Class?不可访问的属性 serialize(unserialize($x)) $x;serialize(unserialize($x)) ! $x;雾现__PHP_Incomplete_Class 对象与其序列化文本的差异试构造 __PHP__Incomplete_Class 对象…...

TempleteMethod
TempleteMethod 动机 在软件构建过程中,对于某一项任务,它常常有稳定的整体操作结构,但各个子步骤却有很多改变的需求,或者由于固有的原因 (比如框架与应用之间的关系)而无法和任务的整体结构同时实现。如…...
1558. 得到目标数组的最少函数调用次数
1558. 得到目标数组的最少函数调用次数 原题链接:完成情况:解题思路:参考代码: 原题链接: 1558. 得到目标数组的最少函数调用次数 https://leetcode.cn/problems/minimum-numbers-of-function-calls-to-make-target…...

子域名扫描, 后台扫描
子域名和后台扫描 一, 子域名扫描 在渗透测试的早期阶段,子域名扫描是一个非常重要的步骤,它有助于识别目标组织的网络结构和在线资源。 子域名扫描应该在获得适当的权限和授权的情况下进行,以确保所有活动都是合法和合规的。 1. 原因与目…...

毛玻璃带有光影效果的卡片
效果展示 页面结构组成 从效果展示可以看到,页面的主要元素是卡片,卡片的内容呈现上都是比较常规的布局,只是卡片上带有光影效果。 CSS / JavaScript 知识点 transformVanillaTilt.js 使用 页面基础结构实现 <div class"contain…...

【Java】面向过程和面向对象思想||对象和类
1.面向过程和面向对象思想 两者都贯穿于软件分析、设计和开发的各个阶段,对应面向对象就分别称为面向对象的分析(OOA)、面向对象的设计(OOD)和面向对象的编程(OOP)。C语言是一种典型的面向过程语…...
孤举者难起,众行者易趋,openGauss 5.1.0版本正式发布!
📢📢📢📣📣📣 哈喽!大家好,我是【IT邦德】,江湖人称jeames007,10余年DBA及大数据工作经验 一位上进心十足的【大数据领域博主】!😜&am…...
软考——软件设计师中级2023年11月备考(1.计算机组成原理)
一、计算机组成原理 1.数据的表示 1.1 十进制转R进制 方法:对十进制数除R取余,最后对余数取倒序 如: 1.2 原码反码补码 1.3 浮点数 1.4 校验码 —— 海明码 (非重点,了解即可) 海明码的构成方法&…...
前端JavaScript入门到精通,javascript核心进阶ES6语法、API、js高级等基础知识和实战 —— Web APIs(四)
思维导图 一、日期对象 1.1 实例化 实例化,默认得到当前时间,也可以指定时间 1.2 日期对象方法 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible&q…...

【前端】HTML5 Audio 预加载 按照队列顺序播放音频, 可以陆续往队列中加内容
【前端】Audio 按照队列顺序播放音频, 可以陆续往队列中加内容 var 音频库 {} var 当前音频集合 [] /*** 将文本添加到队列中* 持续去播放* 播放过的音频会自动从队列中删除* * 已规划* 要保障同时进行加载的数据不能超过5个(线程池 5)* * param 文本*/播放音频队列(文本){i…...

【单片机】13-实时时钟DS1302
1.RTC的简介 1.什么是实时时钟(RTC) (rtc for real time clock) (1)时间点和时间段的概念区分 (2)单片机为什么需要时间点【一定的时间点干什么事情】 (3)RTC如何存在于…...

springboot和vue:十三、VueX简介与安装与推荐视频+前端数据模拟MockJS
VueX简介与安装与推荐视频 VueX用于管理分散在vue各个组件中的数据。每一个VueX的核心都是一个store,当store中的状态发生变化时,与之绑定的视图也将重新渲染。store中的状态不允许被直接修改,只能显示提交mutationVueX中有五个重要的概念&a…...
[React] Zustand状态管理库
文章目录 1.Zustand介绍2.创建一个store3.使用方法3.1 获取状态3.2 更新状态3.3 访问存储状态3.4 处理异步数据3.5 在状态中访问和存储数组3.6 持续状态 4.总结 1.Zustand介绍 状态管理一直是现代程序应用中的重要组成部分, Zustand使用 hooks 来管理状态无需样板代码。 更少…...

【ChatGPT】ChatGPT发展历史
更多优质文章请看底部:ChatGPT与日本首相交流核废水事件-精准Prompt... hello,我是小索奇,在AI日益庞大的环境下,接下来将为大家不断的ChatGPT学习 ChatGPT使用了 Transformer 结构,建立在 OpenAI的 GPT-3.5 大型语言模…...
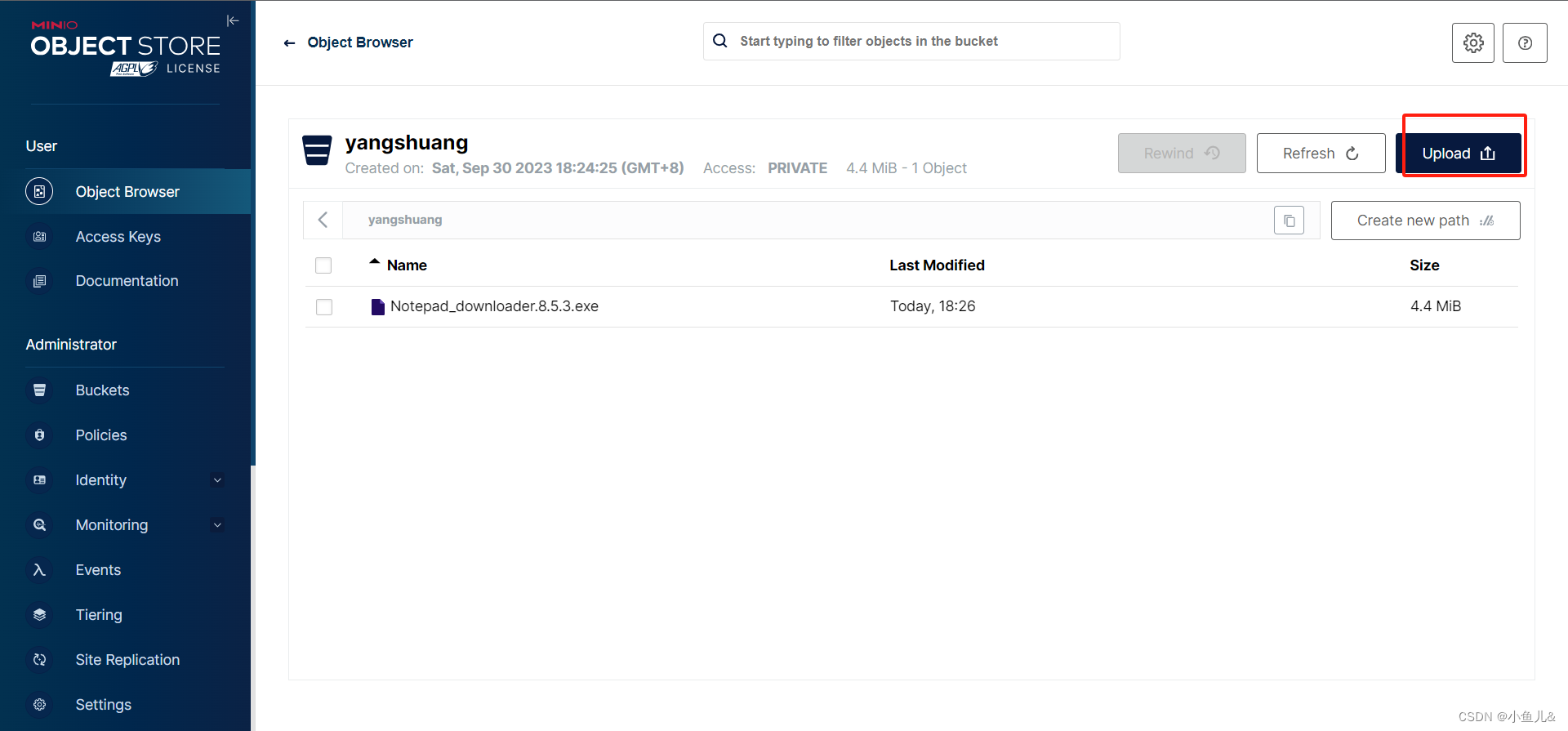
分布式文件存储系统Minio实战
分布式文件系统应用场景 互联网海量非结构化数据的存储需求电商网站:海量商品图片视频网站:海量视频文件网盘 : 海量文件社交网站:海量图片 1. Minio介绍 MinIO 是一个基于Apache License v2.0开源协议的对象存储服务。它兼容亚马逊S3云存…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

算法—栈系列
一:删除字符串中的所有相邻重复项 class Solution { public:string removeDuplicates(string s) {stack<char> st;for(int i 0; i < s.size(); i){char target s[i];if(!st.empty() && target st.top())st.pop();elsest.push(s[i]);}string ret…...
