【算法优选】双指针专题——贰
文章目录
- 😎前言
- 🌲[快乐数](https://leetcode.cn/problems/happy-number/)
- 🚩题目描述
- 🚩题⽬分析:
- 🚩算法思路:
- 🚩代码实现:
- 🎋[盛水最多的容器](https://leetcode.cn/problems/container-with-most-water/)
- 🚩题目描述
- 🚩算法思路:
- 🚩代码实现
- 🎍[有效三角形个数](https://leetcode.cn/problems/valid-triangle-number/)
- 🚩题目描述
- 🚩算法思路:
- 🚩代码实现:
- ⭕总结
😎前言
常⻅的双指针有两种形式,⼀种是对撞指针,⼀种是左右指针
对撞指针:⼀般⽤于顺序结构中,也称左右指针。
-
对撞指针从两端向中间移动。⼀个指针从最左端开始,另⼀个从最右端开始,然后逐渐往中间逼近。
-
对撞指针的终⽌条件⼀般是两个指针相遇或者错开(也可能在循环内部找到结果直接跳出循环),也就是:
left == right (两个指针指向同⼀个位置)
left > right (两个指针错开)
快慢指针:⼜称为⻳兔赛跑算法,其基本思想就是使⽤两个移动速度不同的指针在数组或链表等序列结构上移动。
这种⽅法对于处理环形链表或数组⾮常有⽤。其实不单单是环形链表或者是数组,如果我们要研究的问题出现循环往复的情况时,均可考虑使⽤快慢指针的思想。快慢指针的实现⽅式有很多种,最常⽤的⼀种就是:
- 在⼀次循环中,每次让慢的指针向后移动⼀位,⽽快的指针往后移动两位,实现⼀快⼀慢
🌲快乐数
🚩题目描述
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」 定义为:
- 对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。
- 然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。
- 如果这个过程 结果为 1,那么这个数就是快乐数。
如果 n 是 快乐数 就返回 true ;不是,则返回 false 。
-
示例 1:
输入:n = 19
输出:true
解释:
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1 -
示例 2:
输入:n = 2
输出:false
解释:(这⾥省去计算过程,只列出转换后的数)
2 -> 4 -> 16 -> 37 -> 58 -> 89 -> 145 -> 42 -> 20 -> 4 -> 16
往后就不必再计算了,因为出现了重复的数字,最后结果肯定不会是 1
class Solution {public boolean isHappy(int n) {}
}
🚩题⽬分析:
为了⽅便叙述,将「对于⼀个正整数,每⼀次将该数替换为它每个位置上的数字的平⽅和」这⼀个操作记为x 操作;
题⽬告诉我们,当我们不断重复 x 操作的时候,计算⼀定会「死循环」,死的⽅式有两种:
- 情况⼀:⼀直在1 中死循环,即1 -> 1 -> 1 -> 1…
- 情况⼆:在历史的数据中死循环,但始终变不到1
由于上述两种情况只会出现⼀种,因此,只要我们能确定循环是在「情况⼀」中进⾏,还是在「情况⼆」中进⾏,就能得到结果
简单证明:
-
经过⼀次变化之后的最⼤值 9^2 * 10 = 810 ( 2^31-1=2147483647 。选⼀个更⼤的最⼤ 9999999999),也就是变化的区间在 [1, 810] 之间;
-
根据「鸽巢原理」,⼀个数变化 811 次之后,必然会形成⼀个循环;
-
因此,变化的过程最终会⾛到⼀个圈⾥⾯,因此可以⽤「快慢指针」来解决
🚩算法思路:
根据上述的题⽬分析,我们可以知道,当重复执⾏ x 的时候,数据会陷⼊到⼀个「循环」之中。⽽「快慢指针」有⼀个特性,就是在⼀个圆圈中,快指针总是会追上慢指针的,也就是说他们总会相遇在⼀个位置上。如果相遇位置的值是 1,那么这个数⼀定是快乐数;如果相遇位置不是 1 的话,那么就不是快乐数
补充知识:
如何求⼀个数n每个位置上的数字的平⽅和。
- 把数 n 每⼀位的数提取出来:
循环迭代下⾯步骤:
int t = n % 10 提取个位;
n /= 10 ⼲掉个位;
直到 n 的值变为 0 ;
- 提取每⼀位的时候,⽤⼀个变量 tmp 记录这⼀位的平⽅与之前提取位数的平⽅和
tmp = tmp + t * t
🚩代码实现:
class Solution
{// 返回 n 这个数每⼀位上的平⽅和public int bitSum(int n) {int sum = 0;while(n != 0) {int t = n % 10;sum += t * t;n /= 10;}return sum;}public boolean isHappy(int n) {int slow = n;int fast = bitSum(n);while(slow != fast) {//走一步slow = bitSum(slow);//走两步fast = bitSum(bitSum(fast));}return slow == 1;}
}
🎋盛水最多的容器
🚩题目描述
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
-
示例 1:
输入:[1,8,6,2,5,4,8,3,7]
输出:49
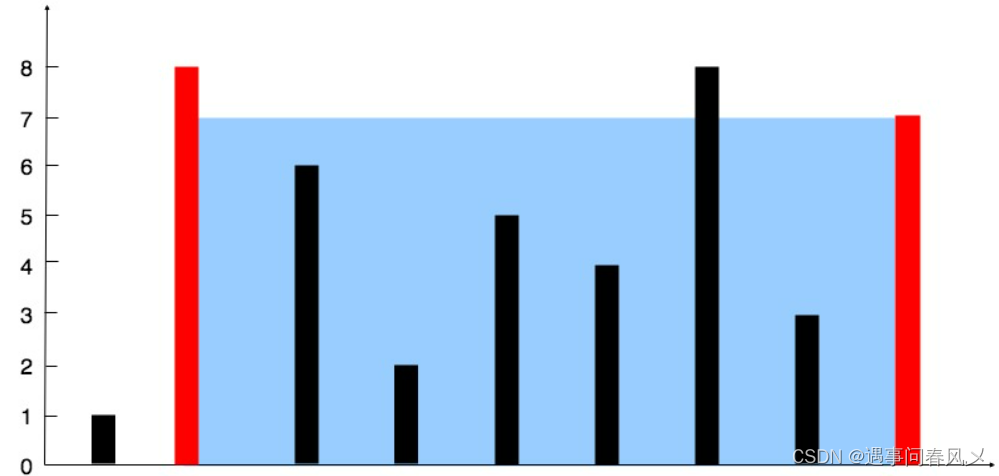 解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。 -
示例 2:
输入:height = [1,1]
输出:1
class Solution {public int maxArea(int[] height) {}
}
🚩算法思路:
设两个指针 left , right 分别指向容器的左右两个端点,此时容器的容积
v = (right - left) * min( height[right], height[left])
容器的左边界为 height[left] ,右边界为 height[right] 。为了⽅便叙述,我们假设「左边边界」⼩于「右边边界」。
如果此时我们固定⼀个边界,改变另⼀个边界,⽔的容积会有如下变化形式:
-
容器的宽度⼀定变⼩。
-
由于左边界较⼩,决定了⽔的⾼度。如果改变左边界,新的⽔⾯⾼度不确定,但是⼀定不会超过右边的柱⼦⾼度,因此容器的容积可能会增⼤。
-
如果改变右边界,⽆论右边界移动到哪⾥,新的⽔⾯的⾼度⼀定不会超过左边界,也就是不会超过现在的⽔⾯⾼度,但是由于容器的宽度减⼩,因此容器的容积⼀定会变⼩的。
由此可⻅,左边界和其余边界的组合情况都可以舍去。所以我们可以 left++ 跳过这个边界,继续去判断下⼀个左右边界。
当我们不断重复上述过程,每次都可以舍去⼤量不必要的枚举过程,直到 left 与 right 相遇。期间产⽣的所有的容积⾥⾯的最⼤值,就是最终答案
🚩代码实现
public class Solution {public int maxArea(int[] height) {int left = 0, right = height.length - 1, ret = 0;while(left < right) {int v = Math.min(height[left], height[right]) * (right - left);ret = Math.max(ret, v);if(height[left] < height[right]) {left++;} else {right--;}}return ret;}
}
🎍有效三角形个数
🚩题目描述
给定一个包含非负整数的数组 nums ,返回其中可以组成三角形三条边的三元组个数。
-
示例 1:
输入: nums = [2,2,3,4]
输出: 3
解释:有效的组合是:
2,3,4 (使用第一个 2)
2,3,4 (使用第二个 2)
2,2,3 -
示例 2:
输入: nums = [4,2,3,4]
输出: 4
class Solution {public int triangleNumber(int[] nums) {}
}
🚩算法思路:
先将数组排序。我们固定⼀个「最⻓边」,然后在⽐这条边⼩的有序数组中找
出⼀个⼆元组,使这个⼆元组之和⼤于这个最⻓边。由于数组是有序的,我们可以利⽤「对撞指针」来优化。
设最⻓边枚举到 i 位置,区间 [left, right] 是 i 位置左边的区间(也就是⽐它⼩的区
间):
- 如果 nums[left] + nums[right] > nums[i] :
▪ 说明 [left, right - 1] 区间上的所有元素均可以与 nums[right] 构成⽐ nums[i]⼤的⼆元组
▪ 满⾜条件的有right - left 种
▪ 此时 right 位置的元素的所有情况相当于全部考虑完毕,right-- ,进⼊下⼀轮判断
- 如果 nums[left] + nums[right] <= nums[i] :
▪ 说明 left 位置的元素是不可能与 [left + 1, right] =位置上的元素构成满⾜条件 的⼆元组
▪ left 位置的元素可以舍去, left++ 进⼊下轮循环
🚩代码实现:
class Solution {public int triangleNumber(int[] nums) {// 1. 优化:排序Arrays.sort(nums);// 2. 利⽤双指针解决问题int ret = 0, n = nums.length;// 先固定最⼤的数for(int i = n - 1; i >= 2; i--) {// 利⽤双指针快速统计出符合要求的三元组的个数int left = 0;int right = i - 1;while(left < right) {if(nums[left] + nums[right] > nums[i]) {ret += right - left;right--;} else {left++;}}}return ret;}
}
⭕总结
关于《【算法优选】双指针专题——贰》就讲解到这儿,感谢大家的支持,欢迎各位留言交流以及批评指正,如果文章对您有帮助或者觉得作者写的还不错可以点一下关注,点赞,收藏支持一下!一起加油
相关文章:

【算法优选】双指针专题——贰
文章目录 😎前言🌲[快乐数](https://leetcode.cn/problems/happy-number/)🚩题目描述🚩题⽬分析:🚩算法思路:🚩代码实现: 🎋[盛水最多的容器](https://leetco…...

AI智能电话机器人实用吗
近几年,人工智能得到很大的发展,同时语音识别技术的不断完善,很多以语音识别为基础的应用涌现出来,尤其是最近3年,出现了很多智能电话机器人。百度开发者大会上展示了百度智能客服也吸引了很多人对智能电话机器人的兴趣…...
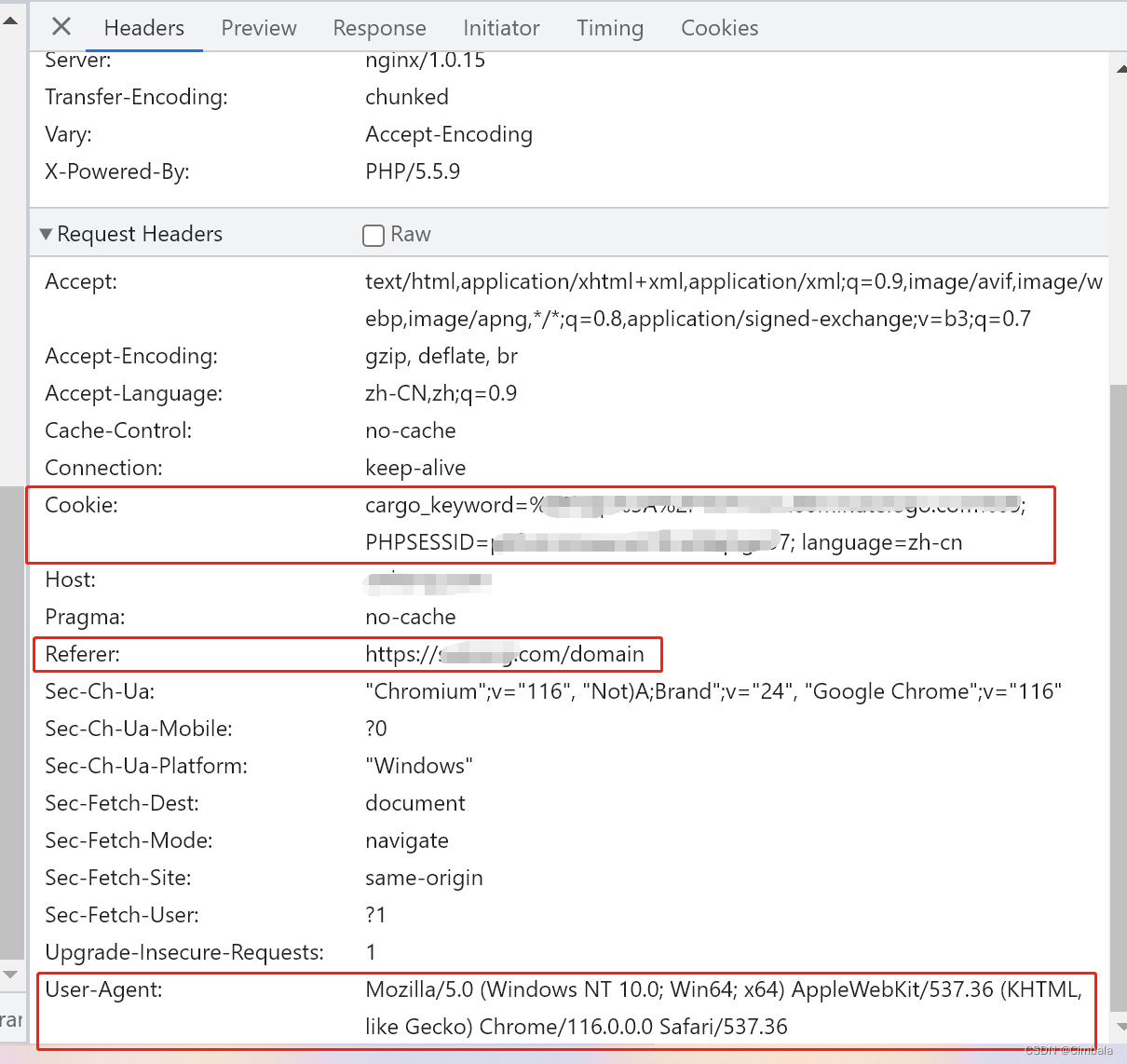
网络爬虫--伪装浏览器
从用户请求的Headers反反爬 在访问某些网站的时候,网站通常会用判断访问是否带有头文件来鉴别该访问是否为爬虫,用来作为反爬取的一种策略。很多网站都会对Headers的User-Agent进行检测,还有一部分网站会对Referer进行检测(一些资…...
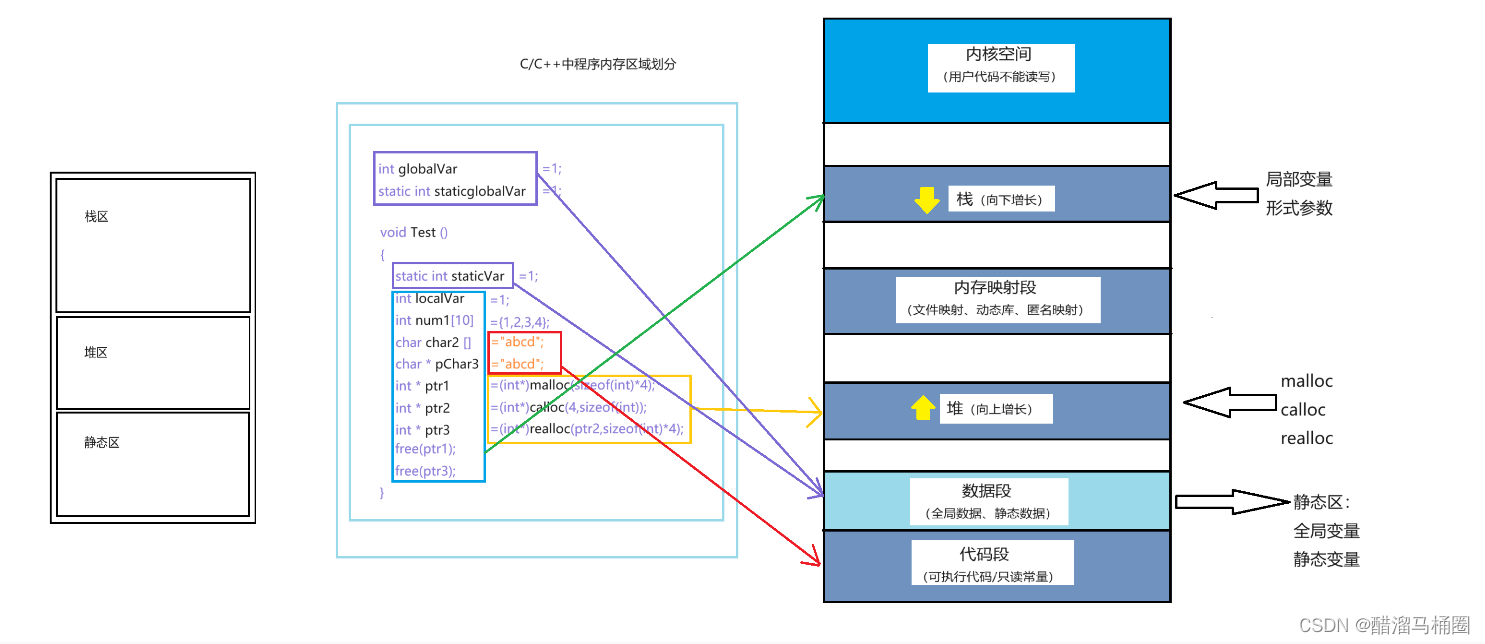
C/C++程序的内存开辟
前面我们说过,计算机中内存分为三个区域:栈区,堆区,静态区 但是这只是个简化的版本,接下来我们仔细看看内存区域的划分 C/C程序内存分配的几个区域: 栈区(stack):在执行…...

【Java 进阶篇】JDBC DriverManager 详解
JDBC(Java Database Connectivity)是 Java 标准库中用于与数据库进行交互的 API。它允许 Java 应用程序连接到各种不同的数据库管理系统(DBMS),执行 SQL 查询和更新操作,以及处理数据库事务。在 JDBC 中&am…...

2023年Linux总结常用命令
1.常用命令 1.1创建文件夹 mkdir -p forever/my 1.2当前目录 pwd 1.3创建文件 touch 1.txt 1.4查看文件 cat 1.txt 1.5复制文件 说明:-r是复制文件夹 cp -r my myCopy 1.6删除文件 说明:-r带包删除文件夹,-f表示强制删除(保存问题) rm -r…...
Mybatis3详解 之 全局配置文件详解
1、全局配置文件 前面我们看到的Mybatis全局文件并没有全部列举出来,所以这一章我们来详细的介绍一遍,Mybatis的全局配置文件并不是很复杂,它的所有元素和代码如下所示: <?xml version"1.0" encoding"UTF-8&…...

力扣-345.反转字符串中的元音字母
Idea 将s中的元音字母存在字符串sv中,并且使用一个数组依次存储元音字母的下标。 然后将字符串sv进行反转,并遍历元音下标数组,将反转后的字符串sv依次插入到源字符串s中 AC Code class Solution { public:string reverseVowels(string s) {…...

643. 子数组最大平均数I(滑动窗口)
目录 一、题目 二、代码 一、题目 643. 子数组最大平均数 I - 力扣(LeetCode) 二、代码 class Solution { public:double findMaxAverage(vector<int>& nums, int k) {double Average INT_MIN;double sum nums[0];int left 0, right 0…...

Java 21 新特性:虚拟线程(Virtual Threads)
I often take exercise. Why only yesterday I had breakfast in bed. 在Java 21中,引入了虚拟线程(Virtual Threads)来简化和增强并发性,这使得在Java中编程并发程序更容易、更高效。 虚拟线程,也称为“用户模式线程…...

18scala笔记
Scala2.12 视频地址 1 入门 1.1 发展历史 … 1.2 Scala 和 Java Scala Java 编写代码使用scalac编译成.class字节码文件scala .class文件 执行代码 1.3 特点 1.4 安装 视频地址 注意配置好环境变量 简单代码 1.5 编译文件 编译scala文件会产生两个.class文件 使用java…...

【LeetCode周赛】LeetCode第365场周赛
目录 有序三元组中的最大值 I有序三元组中的最大值 II无限数组的最短子数组 有序三元组中的最大值 I 给你一个下标从 0 开始的整数数组nums。 请你从所有满足 i < j < k 的下标三元组 (i, j, k) 中,找出并返回下标三元组的最大值。如果所有满足条件的三元组的…...
响应式设计的实现方式
一. 什么是响应式 响应式网站设计是一种网络页面设计布局。页面的设计与开发应当根据用户行为以及设备环境(系统平台,屏幕尺寸,屏幕定向等)进行相应的响应和调整。 响应式网站常见特点: 1. 同时适配PC平板手机。 2…...

PHP 反序列化漏洞:__PHP_Incomplete_Class 与 serialize(unserialize($x)) !== $x;
文章目录 参考环境声明__PHP_Incomplete_Class灵显为什么需要 __PHP_Incomplete_Class?不可访问的属性 serialize(unserialize($x)) $x;serialize(unserialize($x)) ! $x;雾现__PHP_Incomplete_Class 对象与其序列化文本的差异试构造 __PHP__Incomplete_Class 对象…...

TempleteMethod
TempleteMethod 动机 在软件构建过程中,对于某一项任务,它常常有稳定的整体操作结构,但各个子步骤却有很多改变的需求,或者由于固有的原因 (比如框架与应用之间的关系)而无法和任务的整体结构同时实现。如…...
1558. 得到目标数组的最少函数调用次数
1558. 得到目标数组的最少函数调用次数 原题链接:完成情况:解题思路:参考代码: 原题链接: 1558. 得到目标数组的最少函数调用次数 https://leetcode.cn/problems/minimum-numbers-of-function-calls-to-make-target…...

子域名扫描, 后台扫描
子域名和后台扫描 一, 子域名扫描 在渗透测试的早期阶段,子域名扫描是一个非常重要的步骤,它有助于识别目标组织的网络结构和在线资源。 子域名扫描应该在获得适当的权限和授权的情况下进行,以确保所有活动都是合法和合规的。 1. 原因与目…...

毛玻璃带有光影效果的卡片
效果展示 页面结构组成 从效果展示可以看到,页面的主要元素是卡片,卡片的内容呈现上都是比较常规的布局,只是卡片上带有光影效果。 CSS / JavaScript 知识点 transformVanillaTilt.js 使用 页面基础结构实现 <div class"contain…...

【Java】面向过程和面向对象思想||对象和类
1.面向过程和面向对象思想 两者都贯穿于软件分析、设计和开发的各个阶段,对应面向对象就分别称为面向对象的分析(OOA)、面向对象的设计(OOD)和面向对象的编程(OOP)。C语言是一种典型的面向过程语…...
孤举者难起,众行者易趋,openGauss 5.1.0版本正式发布!
📢📢📢📣📣📣 哈喽!大家好,我是【IT邦德】,江湖人称jeames007,10余年DBA及大数据工作经验 一位上进心十足的【大数据领域博主】!😜&am…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

Java数组Arrays操作全攻略
Arrays类的概述 Java中的Arrays类位于java.util包中,提供了一系列静态方法用于操作数组(如排序、搜索、填充、比较等)。这些方法适用于基本类型数组和对象数组。 常用成员方法及代码示例 排序(sort) 对数组进行升序…...

算法—栈系列
一:删除字符串中的所有相邻重复项 class Solution { public:string removeDuplicates(string s) {stack<char> st;for(int i 0; i < s.size(); i){char target s[i];if(!st.empty() && target st.top())st.pop();elsest.push(s[i]);}string ret…...

边缘计算网关提升水产养殖尾水处理的远程运维效率
一、项目背景 随着水产养殖行业的快速发展,养殖尾水的处理成为了一个亟待解决的环保问题。传统的尾水处理方式不仅效率低下,而且难以实现精准监控和管理。为了提升尾水处理的效果和效率,同时降低人力成本,某大型水产养殖企业决定…...
