ABC322刷题记
ABC322刷题记
T1.A
A - First ABC 2。
妥妥的简单题……
用find函数做就行。(如果不存在那个子串就返回-1,否则返回第一次出现位置)
注意题目中编号是从1开始的。
时间复杂度:O(log(n))。find函数有一定代价,我记得是log。
#include<bits/stdc++.h>
using namespace std;
string str="";
int n=0;
int main(){
scanf("%d",&n);
cin>>str;
//输入
str=" "+str;
//处理:把0开头改成1开头
printf("%d\n",str.find("ABC"));
//输出答案
return 0;
}
T2.B
B - Prefix and Suffix。
前两题都一样简单。
用substr截取出t中与s长度相同的前缀和后缀,分别和s比较即可。
时间复杂度先不算了,因为肯定够。
#include<bits/stdc++.h>
using namespace std;
int m=0,n=0;
string s="",t="";
int main(){
scanf("%d%d",&n,&m);
cin>>s>>t;
//输入
string front=t.substr(0,n),rear=t.substr(m-n,n);
//去除前缀与后缀
if(front==s&&rear==s){
printf("0\n");
}else{
if(front==s&&rear!=s){
printf("1\n");
}else{
if(front!=s&&rear==s){
printf("2\n");
}else{
printf("3\n");
}
}
}
//对号入座,输出不错
return 0;
}
T3.C
C - Festival。
还是辣墨简单……
用b数组记录某一天是否有烟花,在用ans数组从后往前算,其中ans[i]表示离第i天最近并且时间不比第i天早的放烟花的日子与第i天相差多少。
最后从1到n输出ans的对应项即可。
时间复杂度:O(n),应该是最优的思路了。
#include<bits/stdc++.h>
#define M 220000
#define N 220000
using namespace std;
int ans[N]={},a[M]={},m=0,n=0;
bool b[N]={};
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
scanf("%d",&a[i]);
b[a[i]]=true;
}
//输入,并维护b数组
for(int i=n;i>=1;i--){
if(b[i]==true){
ans[i]=0;
//①当前这一天就有烟花:距离为0
}else{
ans[i]=ans[i+1]+1;
//②当前这一天没有烟花:比明天的距离多一天
}
}
//计算ans
for(int i=1;i<=n;i++){
printf("%d\n",ans[i]);
}
//输出答案
return 0;
}
T4.D
D - Polyomino。
客观来说,我这道题没做出来真有些丢人。
其实就是一个dfs,但是一个变量名害我找了1天6小时34分钟……
我们定义一个结构体,存储一块牌,如果一个坐标上有点,就记录为1,否则记录为0。支持项各个方向平移(如果会出格,就返回不能做,否则返回操作成功)、顺时针旋转、逆时针旋转操作,当然还要封装加法(把骨牌拼接起来,其实就是相同坐标的点记录的数相加,如果相加后和为0,就说明这里本来就没有点,如果为1就说明刚好有一个牌上有,如果大于1就说明有多个牌子上面有这个点,当然,只有当3块牌都记起来之后和为1才能说明这种摆法可能合法)、等于号(骨牌完全相同,用于判断拼完之后是不是和满牌相同)。
在dfs中,我们不难证明先旋转(遍历旋转次数,去时顺时针,回时逆时针),在平移(反方向的平移互相作为返回操作)是不会有问题的,当然要注意平移可以项各种方向平移多次。
最终大体流程是这样:使用dfs,遍历三个牌的操作,如果最后拼起来是满牌就说明可以达成目的,直接标记最终答案为“可行”,并一路退出回到主程序,否则继续往下遍历。遍历操做时,先考虑旋转,再考虑平移。最后输出Yes/No即可。
时间复杂度不好算,这里不展开描述,但是数据量都是4、16这类数,估计也没啥事。
#include<bits/stdc++.h>
using namespace std;
struct Info{
int num[4][4];
Info operator+(Info ot){
Info ret={};
for(int i=0;i<4;i++){
for(int j=0;j<4;j++){
ret.num[i][j]=num[i][j]+ot.num[i][j];
}
}
return ret;
}
//拼接
bool operator==(Info ot){
for(int i=0;i<4;i++){
for(int j=0;j<4;j++){
if(num[i][j]!=ot.num[i][j]){
return false;
}
}
}
return true;
}
//判等
bool down(){
for(int i=0;i<4;i++){
if(num[3][i]==1){
return false;
}
}
for(int i=3;i>=1;i--){
for(int j=0;j<4;j++){
num[i][j]=num[i-1][j];
}
}
for(int i=0;i<4;i++){
num[0][i]=0;
}
return true;
}
//下移
bool left(){
for(int i=0;i<4;i++){
if(num[i][0]==1){
return false;
}
}
for(int i=0;i<=2;i++){
for(int j=0;j<4;j++){
num[j][i]=num[j][i+1];
}
}
for(int i=0;i<4;i++){
num[i][3]=0;
}
return true;
}
//左移
bool right(){
for(int i=0;i<4;i++){
if(num[i][3]==1){
return false;
}
}
for(int i=3;i>=1;i--){
for(int j=0;j<4;j++){
num[j][i]=num[j][i-1];
}
}
for(int i=0;i<4;i++){
num[i][0]=0;
}
return true;
}
//右移
bool up(){
for(int i=0;i<4;i++){
if(num[0][i]==1){
return false;
}
}
for(int i=0;i<=2;i++){
for(int j=0;j<4;j++){
num[i][j]=num[i+1][j];
}
}
for(int i=0;i<4;i++){
num[3][i]=0;
}
return true;
}
//上移
void spina(){
Info ret={};
for(int i=0;i<4;i++){
for(int j=0;j<4;j++){
ret.num[i][j]=num[3-j][i];
}
}
memcpy(num,ret.num,sizeof(num));
return;
}
//顺时针旋转
void spinb(){
Info ret={};
for(int i=0;i<4;i++){
for(int j=0;j<4;j++){
ret.num[i][j]=num[j][3-i];
}
}
memcpy(num,ret.num,sizeof(num));
return;
}
//逆时针旋转
};
Info inf[10]={};
bool ans=false;
inline void dfs(int d);
//深度优先搜索用到函数
inline void tmovew(int d);
//遍历旋转,用完后返回原始状态
inline void tmovex(int d);
//遍历横移,用完后返回原始状态
inline void tmovey(int d);
//遍历竖移,用完后返回原始状态
int main(){
inf[4]={{{1,1,1,1},{1,1,1,1},{1,1,1,1},{1,1,1,1}}};
//满牌
for(int i=0;i<4;i++){
string str="";
cin>>str;
for(int j=0;j<4;j++){
if(str[j]=='#'){
inf[1].num[i][j]=1;
}
}
}
for(int i=0;i<4;i++){
string str="";
cin>>str;
for(int j=0;j<4;j++){
if(str[j]=='#'){
inf[2].num[i][j]=1;
}
}
}
for(int i=0;i<4;i++){
string str="";
cin>>str;
for(int j=0;j<4;j++){
if(str[j]=='#'){
inf[3].num[i][j]=1;
}
}
}
//输入,并处理成Info格式
dfs(1);
//dfs
if(ans==false){
printf("No\n");
}else{
printf("Yes\n");
}
//根据答案输出
return 0;
}
inline void dfs(int d){
if(d==4){
//3个骨牌遍历完成
if(inf[1]+inf[2]+inf[3]==inf[4]){
ans=true;
//若相加为满牌,就说明答案可行,直接记录答案为“Yes”,或者说true
}
return;
//递归出口
}
if(ans==true){
return;
//已经找到答案,无需继续遍历
}
tmovew(d);
//开始遍历旋转
return;
}
inline void tmovew(int d){
for(int i=0;i<=3;i++){
for(int j=1;j<=i;j++){
inf[d].spina();
}
//顺时针旋转相应次
tmovex(d);
//往下遍历横移
for(int j=1;j<=i;j++){
inf[d].spinb();
}
//逆时针转回去(回溯)
}
return;
}
inline void tmovex(int d){
for(int i=0;i<=4;i++){
int sum=0;
//尽最大可能地往相应方向移动i次,sum记录实际上操作成功的次数,后面所有的sum都同理
for(int j=1;j<=i;j++){
if(inf[d].left()==true){
sum++;
}
}
//往左移动
tmovey(d);
//往下遍历竖移
for(int j=1;j<=sum;j++){
inf[d].right();
}
//往右移动,也就是回溯
}
for(int i=0;i<=4;i++){
int sum=0;
for(int j=1;j<=i;j++){
if(inf[d].right()==true){
sum++;
}
}
//往右移动
tmovey(d);
//往下遍历竖移
for(int j=1;j<=sum;j++){
inf[d].left();
}
//往左移动,也就是回溯
}
return;
}
inline void tmovey(int d){
for(int i=0;i<=4;i++){
int sum=0;
for(int j=1;j<=i;j++){
if(inf[d].down()==true){
sum++;
}
}
//往下移动
dfs(d+1);
//往下递归
for(int j=1;j<=sum;j++){
inf[d].up();
}
//往上移动,也就是回溯
}
for(int i=0;i<=4;i++){
int sum=0;
for(int j=1;j<=i;j++){
if(inf[d].up()==true){
sum++;
}
}
//往上移动
dfs(d+1);
//往下递归
for(int j=1;j<=sum;j++){
inf[d].down();
}
//往下移动,也就是回溯
}
return;
}
相关文章:

ABC322刷题记
ABC322刷题记 T1.A A - First ABC 2。 妥妥的简单题…… 用find函数做就行。(如果不存在那个子串就返回-1,否则返回第一次出现位置) 注意题目中编号是从1开始的。 时间复杂度:O(log(n))。find函数有一定代价,我记…...
visual studio的安装及scanf报错的解决
visual studio是一款很不错的c语言编译器 下载地址:官网 点击后跳转到以下界面 下滑后点击下载Vasual Sutdio,选择社区版即可 选择位置存放下载文件后,即可开始安装 安装时会稍微等一小会儿。然后会弹出这个窗口,我们选择安装位…...

React生命周期
React的生命周期主要是指React组件从创建到销毁的过程,包括三个阶段:挂载期(实例化期)、更新期(存在期)、卸载期(销毁期) 挂载期: constructor(props&#…...
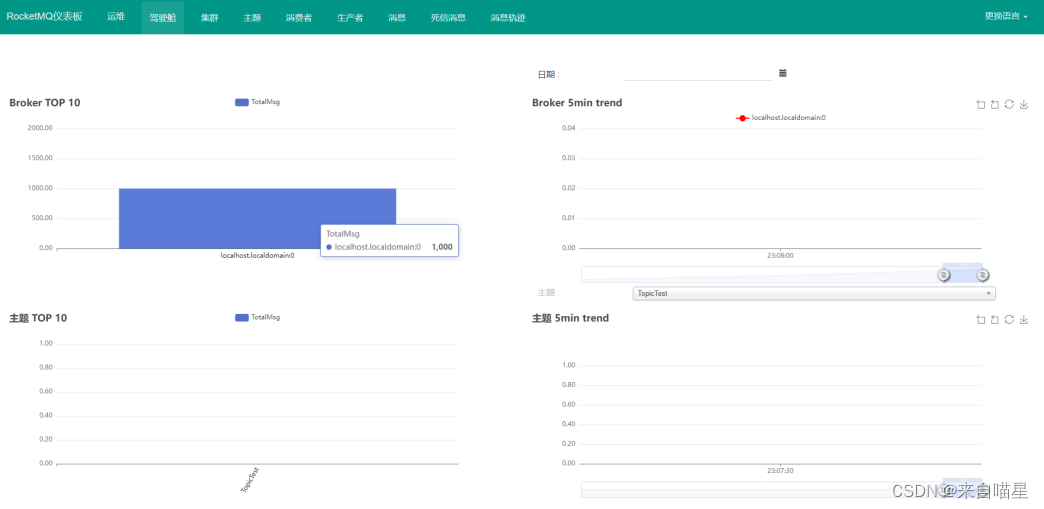
SpringBoot整合RocketMQ笔记
SpringBoot版本为2.3.12.Release RocketMQ对比kafka 学习链接 https://zhuanlan.zhihu.com/p/335216381 代码实战 https://www.cnblogs.com/RedOrange/p/17401238.html Centos安装rocketmq https://blog.csdn.net/chuige2013/article/details/123783612 RocketMQ详细配置与…...
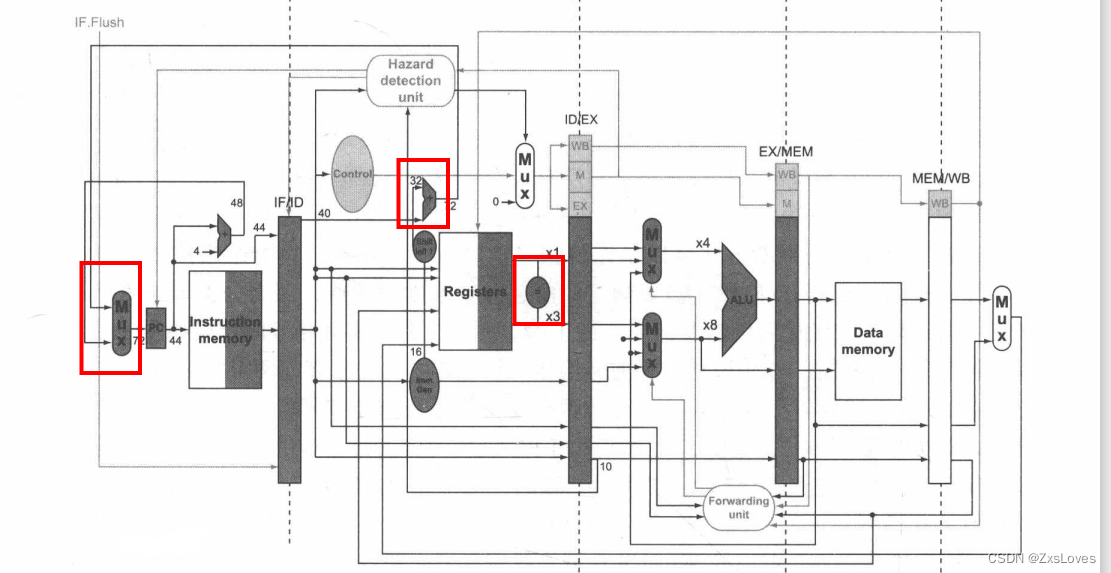
【【萌新的RiscV学习之在写代码之前对于关键路径的分析-11】】
萌新的RiscV学习之在写代码之前对于关键路径的分析-11 首先我们最简单的control 模块 全分段 因为只有分段 , 分开使用之后 , 各个阶段的具体功能才会合理使用 就像是为了后续 “气泡” 赋值 为 0 还有单独比较前递这种 EX : ALUOP ALUSrc …...

A. Sequence with Digits
题目:样例: 输入 8 1 4 487 1 487 2 487 3 487 4 487 5 487 6 487 7输出 42 487 519 528 544 564 588 628 思路: 暴力模拟题,看这数据范围,有些人可能会被唬住,以为是高精度或者容易超时,实际上…...

gitlab配置webhook限制提交注释
一、打开gitlab相关配置项 vim /etc/gitlab/gitlab.rb gitlab_shell[custom_hooks_dir] "/etc/gitlab/custom_hooks" 二、创建相关文件夹 mkdir -p /etc/gitlab/custom_hooks mkdir -p /etc/gitlab/custom_hooks/post-receive.d mkdir -p /etc/gitlab/custom_h…...

蓝桥杯Python scratch C++选拔赛stema个人如何报名?
如果不会操作,可以微信makytony协助。...

Cesium实现动态旋转四棱锥(2023.9.11)
Cesium实现动态悬浮旋转四棱锥效果 2023.9.11 1、引言2、两种实现思路介绍2.1 思路一:添加已有的四棱锥(金字塔)模型实现(简单但受限)2.2 思路二:自定义四棱锥几何模型实现(复杂且灵活ÿ…...
2023最新PS(photoshop)Win+Mac免费下载安装包及教程内置AI绘画-网盘下载
2023最新PS(photoshop)WinMac免费下载安装包及教程内置AI绘画-网盘下载 2023最新PS(photoshop)免费下载安装教程来咯~ 「PhotoShop」全套,winmac: https://pan.quark.cn/s/9d8d8ef5c400#/list/share 所有版本都有 1,复制链接…...

【JAVA】为什么要使用封装以及如何封装
个人主页:【😊个人主页】 系列专栏:【❤️初识JAVA】 前言 Java的封装指的是在一个类中将数据和方法进行封装,使其可以保护起来,只能在该类内部访问,而不允许外部直接访问和修改。这是Java面向对象编程的三…...
18.示例程序(编码器接口测速)
STM32标准库开发-各章节笔记-查阅传送门_Archie_IT的博客-CSDN博客https://blog.csdn.net/m0_61712829/article/details/132434192?spm1001.2014.3001.5501 main.c #include "stm32f10x.h" // Device header #include "Delay.h" #incl…...
【超详细】Fastjson 1.2.24 命令执行漏洞复现-JNDI简单实现反弹shell(CVE-2017-18349)
前言: 看了很多别人关于漏洞复现过程,很多博客过程简洁,有的过程过于复杂,比如看到写java代码,用javac进行编译等等。所以我想写出比较详细的漏洞复现过程。 一,漏洞介绍 1-1 fastjson是什么 fastjson是…...
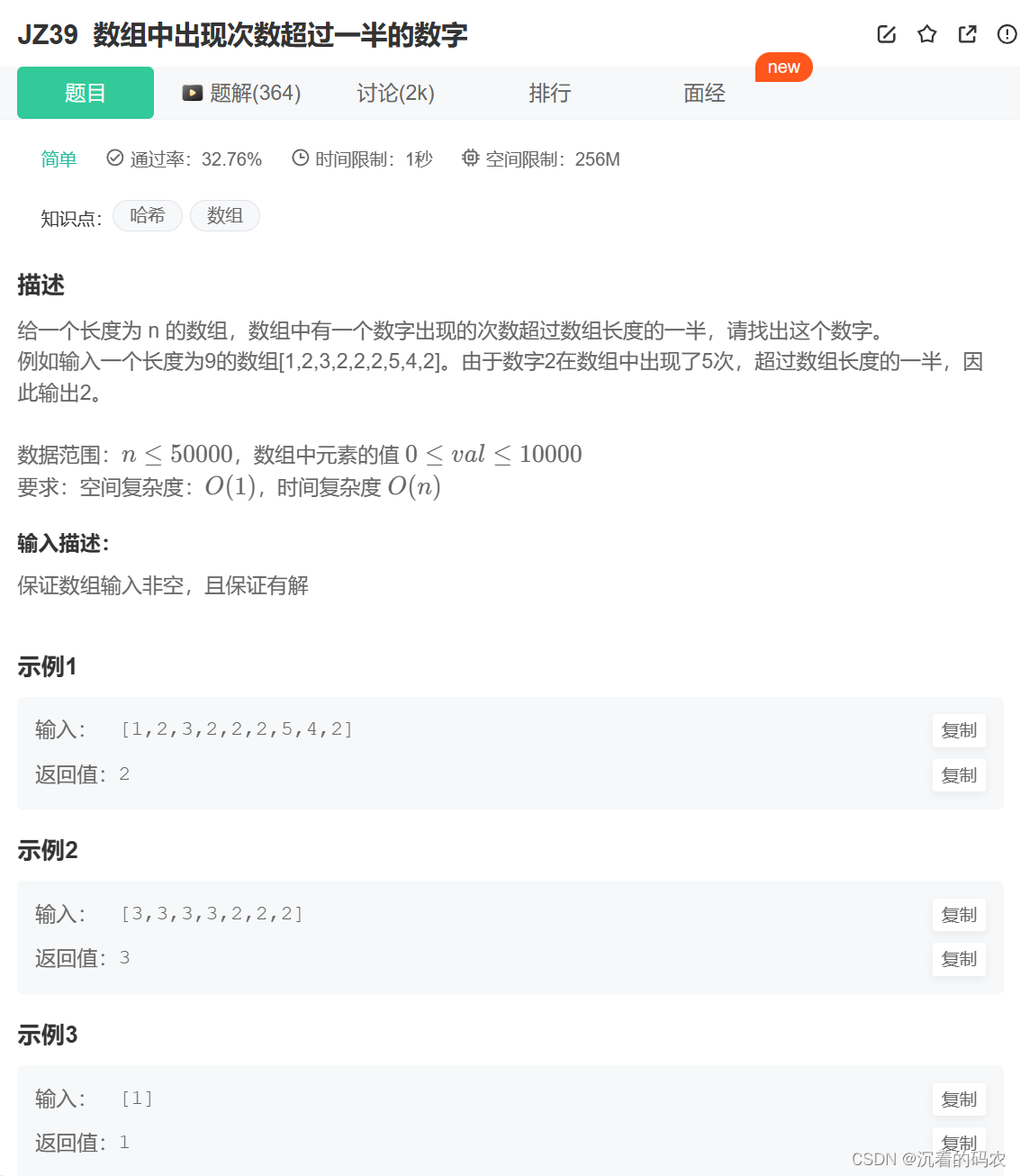
【牛客网】JZ39 数组中出现次数超过一半的数字
题目 思路 思路1 将数组排序,再保证有结果的情况下,此时数组中间的数字就是想要的结果 思路2 在保证有结果的情况下,此时数组的的众数是数组长度的一半以上 所以我们可以通过抵消的做法来找到最终的结果 我们可以从头遍历这个数组,如果两个数不相同,则消去这两个数,最坏的…...

【Mysql】Lock wait timeout exceeded; try restarting transaction
出现这种问题通常是有事务长时间未提交导致的 可以使用以下sql 查询事务进程 然后通过 kill 线程ID 的方式 ,结束该事务 SELECTtrx_id AS 事务ID,trx_mysql_thread_id AS 线程ID,trx_state AS 事务状态,trx_started AS 开始时间,trx_tables_locked AS 锁定的表,trx_query AS …...

python生成中金所期权行权价
参考沪深300股指期权的合约表,写一个工具函数: 使用方法 def get_format_option_gap(value: float, deviation: int 0): # 根据中证1000指数获取点位"""根据标准的行权价,生成不同档位的期权列表,适合中金所:…...

CentOS7.9 安装postgresql
# 添加postgres账户 sudo groupadd postgres sudo useradd -g postgres postgres # 修改postgres账号密码 passwd postgres # 安装postgresql cd ~tar zxvf postgresql-15.3.tar.gz cd postgresql-15.3./configure --prefix/usr/local/pgsql --without-readlinemake -j4 …...

qt线程介绍
目录 介绍 线程类 QThread 方式1 方式2 案例 线程资源释放 介绍 qt为多线程提供了完美的支持,实现多线程一般是从从QTHread中继承定义自己的线程类,QT也提供了QMutexLocker,QwaitCondition等类实现线程同步,与Linux系统或C中的线程库类似…...

记一次用dataframe进行数据清理
总结一下dataframe读取数据库,以及整理数据的过程。分为三个部分:数据读取,数据整理以及数据写入。 1、数据读取 从csv读取读取数据,使用pandas读的read_csv函数,传入两个参数,分别是path文件路径&#x…...
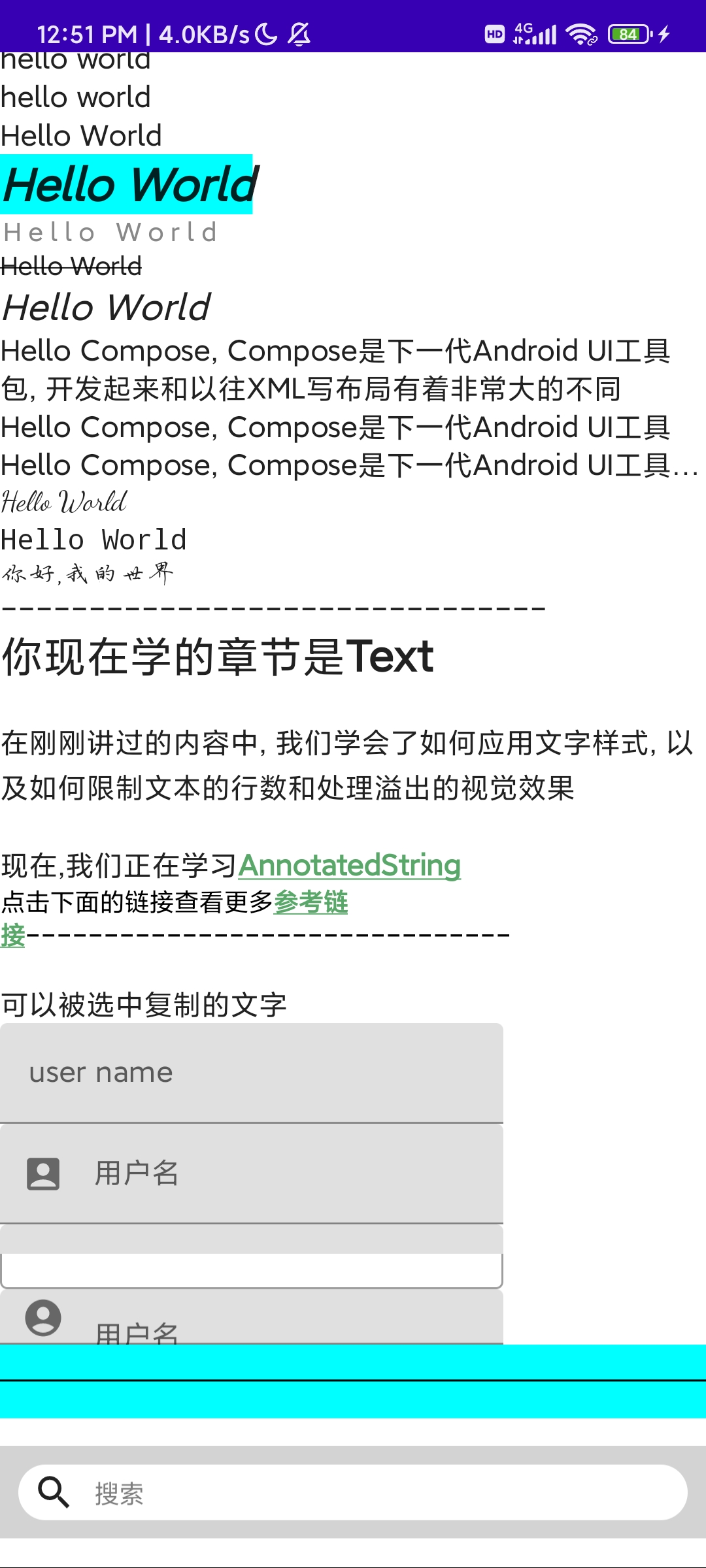
《Jetpack Compose从入门到实战》 第二章 了解常用UI组件
目录 常用的基础组件文字组件图片组件按钮组件选择器组件对话框组件进度条组件 常用的布局组件布局Scaffold脚手架 列表 书附代码 Google的图标库 常用的基础组件 文字组件 Composable fun TestText() {Column(modifier Modifier.verticalScroll(state rememberScrollState…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...

ArcGIS Pro+ArcGIS给你的地图加上北回归线!
今天来看ArcGIS Pro和ArcGIS中如何给制作的中国地图或者其他大范围地图加上北回归线。 我们将在ArcGIS Pro和ArcGIS中一同介绍。 1 ArcGIS Pro中设置北回归线 1、在ArcGIS Pro中初步设置好经纬格网等,设置经线、纬线都以10间隔显示。 2、需要插入背会归线…...
