当前位置： 首页 > news >正文

【改造中序遍历】 538. 把二叉搜索树转换为累加树

news 2026/2/9 13:09:35

538. 把二叉搜索树转换为累加树

解题思路

  • 改造中序遍历算法
  • 因为中序遍历的结果都是有顺序的 升序排序，那么如果先遍历右子树 在遍历左子树 那么结果就是降序的
  • 最后我们设置一个变量 累加所有的中间值 那么得到的结果就是比当前节点大的所有节点的值

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {int sum = 0;public TreeNode convertBST(TreeNode root) {// 改造中序遍历算法traverse(root);return root;}void traverse(TreeNode root){if(root == null){return;}traverse(root.right);sum += root.val;// 每次叠加最大值  比他大的所有节点// 将BST 转化为累加树root.val = sum;traverse(root.left);}
}

相关文章：

【改造中序遍历】 538. 把二叉搜索树转换为累加树

538. 把二叉搜索树转换为累加树 解题思路 改造中序遍历算法因为中序遍历的结果都是有顺序的 升序排序，那么如果先遍历右子树 在遍历左子树 那么结果就是降序的最后我们设置一个变量 累加所有的中间值 那么得到的结果就是比当前节点大的所有节点的值 /*** Definiti…...

编程日记 2023/10/2 22:08:14

2022年11月工作经历

11月 招聘 最近招聘C程序员和黑盒测试员。由于第一次招聘不知道如何处理，不断和同事沟通，摸索出一套简单的规则。C程序员：力扣随机第二题，如果运气不好可以再随机一两次。黑盒测试员：力扣随机第二题或第三题&#xff…...

编程日记 2023/10/2 22:06:10

使用广播信道的数据链路层

使用广播信道的数据链路层 ​ 广播信道可以一对多通信。局域网使用的就是广播信道。局域网最主要的特点就是网络为一个单位所拥有，且地理范围和站点数目有限。局域网可按网络拓扑进行分为星形网、环形网、总线网。传统的以太网就是总线网，后来又演变为星…...

编程日记 2023/10/2 22:05:09

第3章-指标体系与数据可视化-3.1.2-Seaborn绘图库

目录 3.1.2 Seaborn绘图库 1. 带核密度估计的直方图 2. 二元分布图 一维正态分布 联合分布...

编程日记 2023/10/2 22:00:05

excel中将一个sheet表根据条件分成多个sheet表

有如下excel表，要求：按月份将每月的情况放在一个sheet中。 目测有6个月，就应该有6个sheet，每个sheet中体现本月的情况。 一、首先增加一个辅助列，月份，使用month函数即可。 填充此列所有。然后复制【月份】…...

编程日记 2023/10/2 21:59:04

案例突破——再探策略模式

再探设计模式 一、背景介绍二、 思路方案三、过程1. 策略模式基本概念2. 策略模式类图3. 策略模式基本代码策略类抽象策略类Context类客户端 4. 策略模式还可以进行优化的地方5. 对策略模式的优化（配置文件反射） 四、总结五、升华 一、背景介绍 在做项目…...

编程日记 2023/10/2 21:58:03

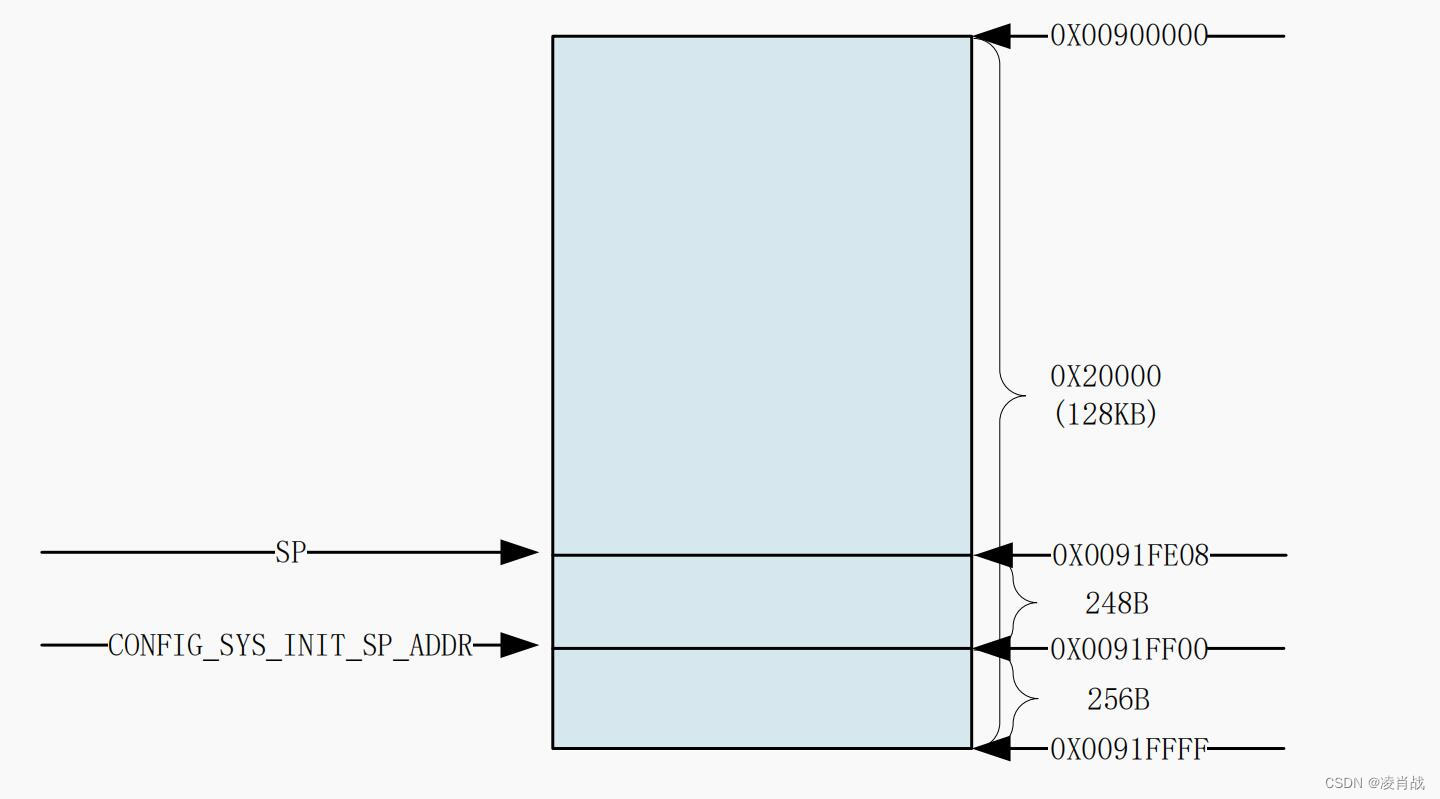
uboot启动流程-涉及lowlevel_init汇编函数

一. uboot启动流程涉及函数 之前文章简单分析了 uboot启动流程的开始，从链接脚本文件 u-boot.lds 中，我们已经知道了入口点是 arch/arm/lib/vectors.S 文件中的 _start函数。 _start函数：调用了 reset 函数，reset 函数内部&…...

编程日记 2023/10/2 21:57:03

质数距离 - 如何在较合理的时间复杂度内求2e9范围内的质数

求l、r之间的质数&#xff0c;范围在2e9&#xff0c;但l、r的差值不大&#xff0c;在1e6范围内 先求出 内的质数&#xff0c;然后拿这个指数去筛[l, r]范围内的即可 #include<bits/stdc.h> #define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0); #define endl \…...

编程日记 2023/10/2 21:56:02

八、3d场景的区域光墙

在遇到区域展示的时候我们就能看到炫酷的区域选中效果&#xff0c;那么代码是怎么编辑的呢&#xff0c;今天咱们就好好说说&#xff0c;下面看实现效果。 思路&#xff1a; 首先&#xff0c;光墙肯定有多个&#xff0c;那么必须要创建一个新的js文件来作为他的原型对象。这个光…...

编程日记 2023/10/2 21:52:59

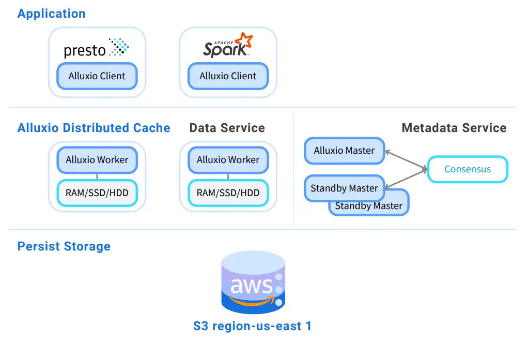
深入探讨 Presto 中的缓存

【squids.cn】 全网zui低价RDS&#xff0c;免费的迁移工具DBMotion、数据库备份工具DBTwin、SQL开发工具等 Presto是一种流行的开源分布式SQL引擎&#xff0c;使组织能够在多个数据源上大规模运行交互式分析查询。缓存是一种典型的提高 Presto 查询性能的优化技术。它为 Prest…...

编程日记 2023/10/2 21:50:57

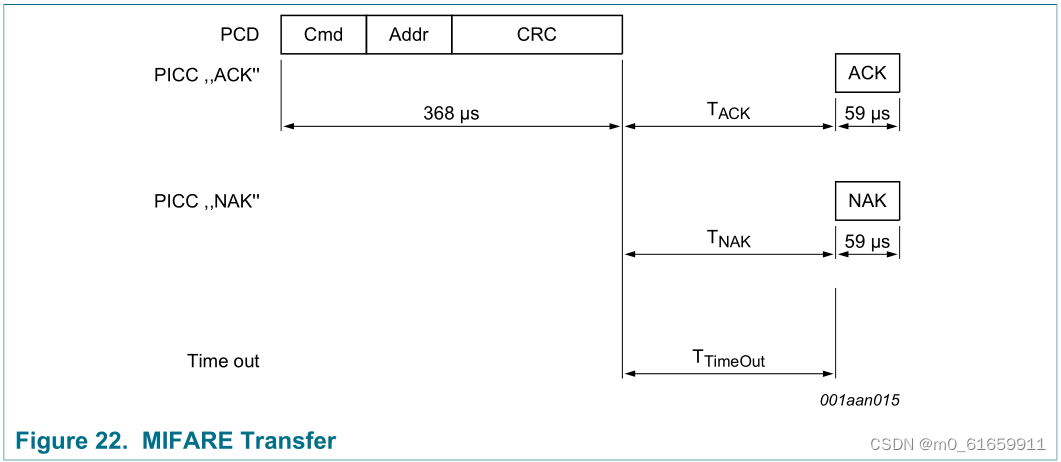
3.物联网射频识别，（高频）RFID应用ISO14443-2协议，（校园卡）Mifare S50卡

一。ISO14443-2协议简介 1.ISO14443协议组成及部分缩略语 &#xff08;1&#xff09;14443协议组成&#xff08;下面的协议简介会详细介绍&#xff09; 14443-1 物理特性 14443-2 射频功率和信号接口 14443-3 初始化和防冲突 &#xff08;分为Type A、Type B两种接口&…...

编程日记 2023/10/2 21:49:56

【IDEA】IDEA 单行注释开头添加空格

操作 打开 IDEA 的 Settings 对话框&#xff08;快捷键为CtrlAltS&#xff09;&#xff1b;在左侧面板中选择Editor -> Code Style -> Java&#xff1b;在右侧面板中选择Code Generation选项卡&#xff1b;将Line comment at first column选项设置为false使注释加在行开…...

编程日记 2023/10/2 21:48:55

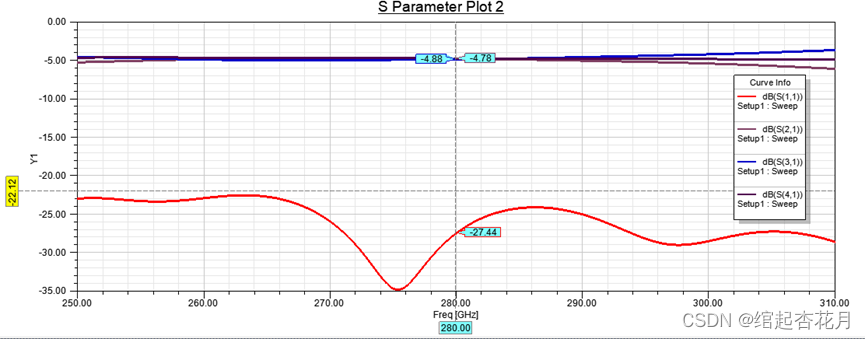
三等分功分器[波导]设计详细教程

想必大家通过阅读相关文献可以发现三等分实现可以有很多不同的方法&#xff0c;这里采用的是先不等分再等分的方式&#xff0c;仅供参考。 主要指标 中心频率为280GHz&#xff0c;采用WR-3频段的标准波导&#xff0c;将2:1不等功率分配耦合器与3dB等功率分配耦合器级联&#…...

编程日记 2023/10/2 21:46:53

Mysql分库分表

1.原理 2.Sharding JDBC 官网https://shardingsphere.apache.org/ 2.1 水平拆分 创建一个新的springboot项目 导入依赖,直接将原本的dependencies给覆盖掉 <dependencies><!-- ShardingJDBC依赖 --><dependency><groupId>org.apache.shardings…...

编程日记 2023/10/2 21:44:51

【算法学习】-【双指针】-【复写零】

LeetCode原题链接&#xff1a;1089. 复写零 下面是题目描述&#xff1a; 给你一个长度固定的整数数组 arr &#xff0c;请你将该数组中出现的每个零都复写一遍&#xff0c;并将其余的元素向右平移。 注意&#xff1a;请不要在超过该数组长度的位置写入元素。请对输入的数组 …...

编程日记 2023/10/2 21:43:50

【算法优选】双指针专题——叁

文章目录 &#x1f60e;前言&#x1f333;[两数之和](https://leetcode.cn/problems/he-wei-sde-liang-ge-shu-zi-lcof/)&#x1f6a9;题目描述&#xff1a;&#x1f6a9;算法思路&#xff1a;&#x1f6a9;算法流程&#xff1a;&#x1f6a9;代码实现 &#x1f384;[三数之和]…...

编程日记 2023/10/2 21:42:49

Java栈的压入、弹出序列（详解）

目录 1.题目描述 2.题解 方法1 方法2 1.题目描述 输入两个整数序列&#xff0c;第一个序列表示栈的压入顺序&#xff0c;请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序&#xff0c;序列4,5,3,2,1是该压栈序…...

编程日记 2023/10/2 21:37:45

RabbitMQ学习笔记（消息发布确认，死信队列，集群，交换机，持久化，生产者、消费者）

MQ&#xff08;message queue&#xff09;&#xff1a;本质上是个队列&#xff0c;遵循FIFO原则&#xff0c;队列中存放的是message&#xff0c;是一种跨进程的通信机制&#xff0c;用于上下游传递消息。MQ提供“逻辑解耦物理解耦”的消息通信服务。使用了MQ之后消息发送上游只…...

编程日记 2023/10/2 21:36:44

PyTorch - 模型训练损失 (Loss) NaN 问题的解决方案

欢迎关注我的CSDN&#xff1a;https://spike.blog.csdn.net/ 本文地址&#xff1a;https://spike.blog.csdn.net/article/details/133378367 在模型训练中&#xff0c;如果出现 NaN 的问题&#xff0c;严重影响 Loss 的反传过程&#xff0c;因此&#xff0c;需要加入一些微小值…...

编程日记 2023/10/2 21:29:38

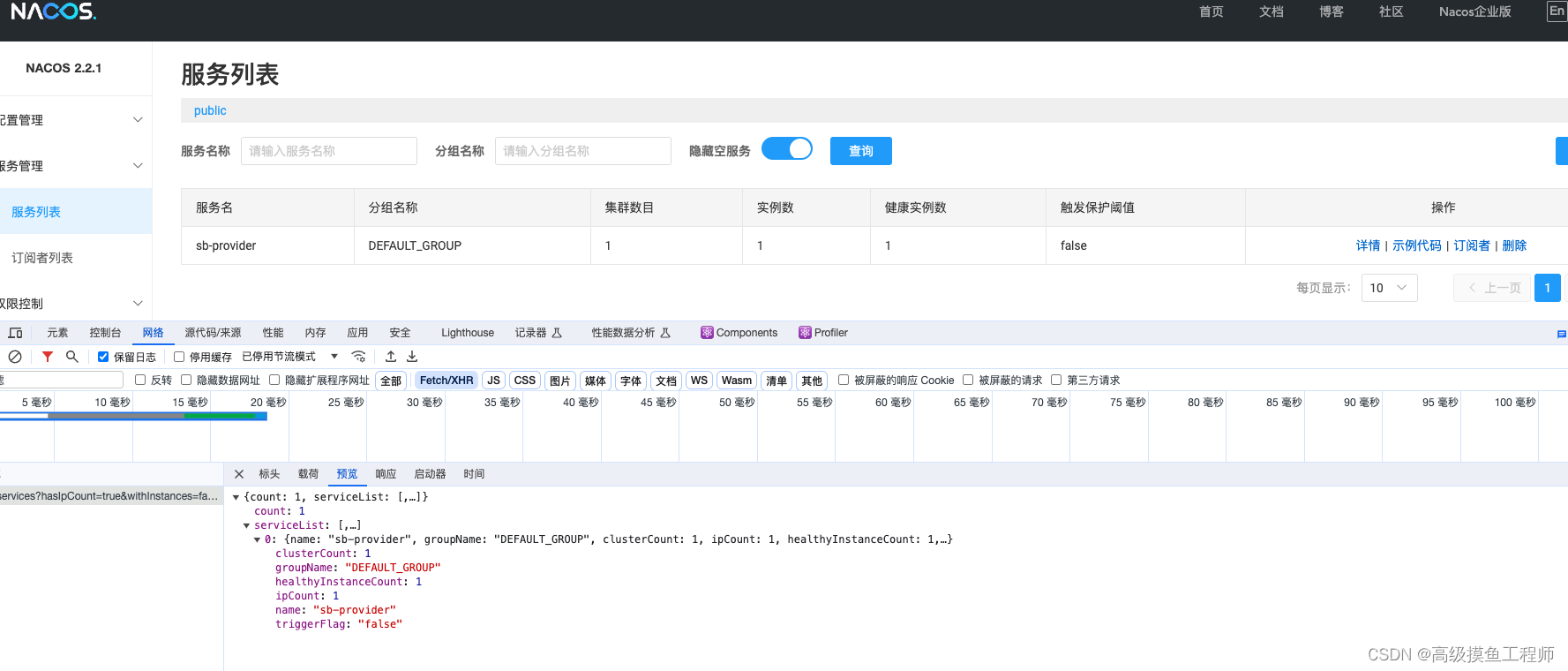
8、Nacos服务注册服务端源码分析（七）

本文收录于专栏 Nacos 中 。 文章目录 前言确定前端路由CatalogController.listDetail()ServiceManager总结 前言 前文我们分析了Nacos中客户端注册时数据分发的设计链路&#xff0c;本文根据Nacos前端页面请求&#xff0c;看下前端页面中的服务列表的数据源于哪里。 确定前端…...

编程日记 2023/10/2 21:28:36

基于算法竞赛的c++编程（28）结构体的进阶应用

结构体的嵌套与复杂数据组织 在C中&#xff0c;结构体可以嵌套使用&#xff0c;形成更复杂的数据结构。例如&#xff0c;可以通过嵌套结构体描述多层级数据关系&#xff1a; struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

编程新知 2025/11/16 19:06:23

CRMEB 框架中 PHP 上传扩展开发：涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云

目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

编程新知 2025/12/30 22:56:56

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”（装配）

船舶制造装配管理现状&#xff1a;装配工作依赖人工经验&#xff0c;装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书&#xff0c;但在实际执行中&#xff0c;工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

编程新知 2026/2/6 2:16:18

【Go语言基础【13】】函数、闭包、方法

文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数&#xff08;函数作为参数、返回值&#xff09; 三、匿名函数与闭包1. 匿名函数&#xff08;Lambda函…...

编程新知 2025/12/8 19:02:25

Python 训练营打卡 Day 47

注意力热力图可视化 在day 46代码的基础上&#xff0c;对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

编程新知 2025/11/24 9:42:16

Linux部署私有文件管理系统MinIO

最近需要用到一个文件管理服务&#xff0c;但是又不想花钱&#xff0c;所以就想着自己搭建一个&#xff0c;刚好我们用的一个开源框架已经集成了MinIO&#xff0c;所以就选了这个 我这边对文件服务性能要求不是太高&#xff0c;单机版就可以 安装非常简单&#xff0c;几个命令就…...

编程新知 2026/2/7 17:45:38

HTTPS证书一年多少钱？

HTTPS证书作为保障网站数据传输安全的重要工具&#xff0c;成为众多网站运营者的必备选择。然而&#xff0c;面对市场上种类繁多的HTTPS证书&#xff0c;其一年费用究竟是多少&#xff0c;又受哪些因素影响呢&#xff1f; 首先&#xff0c;HTTPS证书通常在PinTrust这样的专业平…...

编程新知 2026/1/24 23:35:51

Django RBAC项目后端实战 - 03 DRF权限控制实现

项目背景 在上一篇文章中&#xff0c;我们完成了JWT认证系统的集成。本篇文章将实现基于Redis的RBAC权限控制系统&#xff0c;为系统提供细粒度的权限控制。 开发目标 实现基于Redis的权限缓存机制开发DRF权限控制类实现权限管理API配置权限白名单 前置配置 在开始开发权限…...

编程新知 2025/10/1 4:57:11

路由基础-路由表

本篇将会向读者介绍路由的基本概念。 前言 在一个典型的数据通信网络中&#xff0c;往往存在多个不同的IP网段&#xff0c;数据在不同的IP网段之间交互是需要借助三层设备的&#xff0c;这些设备具备路由能力&#xff0c;能够实现数据的跨网段转发。 路由是数据通信网络中最基…...

编程新知 2026/2/4 13:41:16

大模型——基于Docker+DeepSeek+Dify ：搭建企业级本地私有化知识库超详细教程

基于Docker+DeepSeek+Dify ：搭建企业级本地私有化知识库超详细教程 下载安装Docker Docker官网：https://www.docker.com/ 自定义Docker安装路径 Docker默认安装在C盘，大小大概2.9G，做这行最忌讳的就是安装软件全装C盘，所以我调整了下安装路径。 新建安装目录：E:\MyS…...

编程新知 2026/2/6 11:33:19