P5488 差分与前缀和
传送门:洛谷
前题提要:包含了简单的生成函数思想以及多项式乘法,是一道不可多得的多项式好题.故记录一下.
题意:给定一个长为 n 的序列 a,求出其 k 阶差分或前缀和。结果的每一项都需要对 1004535809取模。
对于差分和前缀和我们分开来讨论.
先讨论前缀和部分:
先列出 A A A序列: ( a 1 , a 2 , . . . , a n ) (a_1,a_2,...,a_n) (a1,a2,...,an),再列出前缀和 S S S序列: ( s 1 , s 2 , . . . , s n ) (s_1,s_2,...,s_n) (s1,s2,...,sn),为了等会的方便起见,我们将这两个序列扩展一下,分别加上一个 a 0 , s 0 a_0,s_0 a0,s0.(并且这两个值规定为0)
存在 s 0 = 0 , s 1 = a 0 + a 1 , s n = a 0 + a 1 + . . . + a n s_0=0,s_1=a_0+a_1,s_n=a_0+a_1+...+a_n s0=0,s1=a0+a1,sn=a0+a1+...+an
我们将其往多项式那边靠,不难发现,如果存在另一个序列 B B B为 ( 1 , 1 , 1...1 ) (1,1,1...1) (1,1,1...1),那么此时我们的 S = A ∗ B S=A*B S=A∗B,也就是 S S S序列是 A A A与 B B B的卷积系数结果.
所以一阶前缀和 S 1 = A 1 ∗ B 1 S1=A1*B1 S1=A1∗B1,那么二阶 S 2 = S 1 ∗ B 1 S2=S1*B1 S2=S1∗B1,因为多项式卷积满足结合律 k k k阶即为 S k = S 1 ∗ B 1 k Sk=S1*B1^k Sk=S1∗B1k.
此时如果多项式的科技比较强,直接套一个多项式快速幂就结束了.
但是显然我的科技树比较差,所以来讨论一下低科技的解法
因为我们无法进行多项式快速幂,所以我们考虑使用生成函数的方法将多项式转为一个函数然后在做考虑.那么此时我们的 B B B就是 1 + x + x 2 + . . . + x n 1+x+x^2+...+x^n 1+x+x2+...+xn,求一下和就是 ( 1 − x n ) / ( 1 − x ) (1-x^n)/(1-x) (1−xn)/(1−x),为了方便起见,我们此时不妨选择 x ∈ ( 0 , 1 ) x\in(0,1) x∈(0,1),那么此时我们的 B B B就是 1 / ( 1 − x ) 1/(1-x) 1/(1−x),那么此时 B k = ( 1 − x ) − k B^k=(1-x)^{-k} Bk=(1−x)−k.
考虑使用扩展二项式定理: ( a + b ) n = a n ∗ ( 1 + b a ) n = a n ∗ ∑ i = 0 ∞ ( n i ) ∗ ( b a ) i (a+b)^n=a^n*(1+\frac{b}{a})^n=a^n*\sum_{i=0}^{\infty}{n\choose i}*(\frac{b}{a})^i (a+b)n=an∗(1+ab)n=an∗i=0∑∞(in)∗(ab)i
那么对于上述式子来说就是 B k = ∑ i = 0 ∞ ( − k i ) ∗ ( − 1 ) i ∗ x i B^k=\sum_{i=0}^{\infty}{-k\choose i}*(-1)^i*x^i Bk=i=0∑∞(i−k)∗(−1)i∗xi ( − k i ) = ( − k ) ∗ ( − k − 1 ) ∗ ( − k − 2 ) ∗ . . . ∗ ( − k − i + 1 ) i ! {-k\choose i}^=\frac{(-k)*(-k-1)*(-k-2)*...*(-k-i+1)}{i!} (i−k)=i!(−k)∗(−k−1)∗(−k−2)∗...∗(−k−i+1) = ( − 1 ) i ∗ k ∗ ( k + 1 ) ∗ ( k + 2 ) ∗ . . . ( k + i − 1 ) i ! =(-1)^i*\frac{k*(k+1)*(k+2)*...(k+i-1)}{i!} =(−1)i∗i!k∗(k+1)∗(k+2)∗...(k+i−1) = ( − 1 ) i ∗ C k + i − 1 i =(-1)^i*C_{k+i-1}^i =(−1)i∗Ck+i−1i
对于 C k + i − 1 i C_{k+i-1}^i Ck+i−1i,显然我们是递推来求和的(注意本题的 k k k很大,只能递推来求和,无法预处理), C k + i − 1 i = C k + i − 2 i − 1 ∗ ( k + i − 1 i ) C_{k+i-1}^i=C_{k+i-2}^{i-1}*(\frac{k+i-1}{i}) Ck+i−1i=Ck+i−2i−1∗(ik+i−1).
那么此时我们的k阶前缀和就到此结束了,只要使用 N T T NTT NTT解决一下多项式乘法即可.
下面讲一下这道题的k阶差分部分.其实大体上的解决方案和前缀和是一样的.
同样考虑得出B序列为 ( 1 , − 1 , 0 , 0 , 0...0 ) (1,-1,0,0,0...0) (1,−1,0,0,0...0) [推导方式和上述一样,此处就不在赘述了].
使用生成函数将 B k B^k Bk序列转化一下就是 ( 1 − x ) k (1-x)^k (1−x)k,使用二项式定理展开就是 ∑ i = 0 ∞ C k i ∗ ( − x ) k \sum_{i=0}^{\infty}C_k^i*(-x)^k ∑i=0∞Cki∗(−x)k,同样递推一下即可.
最后也是拿 N T T NTT NTT做一下多项式乘法即可解决.
下面是具体的代码部分:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
inline void print(__int128 x){if(x<0) {putchar('-');x=-x;}if(x>9) print(x/10);putchar(x%10+'0');
}
#define maxn 1000000
#define int long long
const int mod=1004535809;
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int f[maxn],g1[maxn],g2[maxn];
inline ll get_read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=(x*10%mod+ch-'0')%mod;return x*w;
}
int qpow(int a,int b) {int ans=1;while(b) {if(b&1) ans=ans*a%mod;b>>=1;a=a*a%mod;}return ans;
}
int rev[maxn];
void NTT(int *a,int n,int inv) {for(int i=0;i<=n;i++) if(i<rev[i]) swap(a[i],a[rev[i]]);for(int len=1;len<=(n>>1);len<<=1) {int gn=qpow(inv==1?3:qpow(3,mod-2),(mod-1)/(len<<1));for(int i=0;i<=n;i+=(len<<1)) {int g0=1;for(int j=0;j<=len-1;j++) {int x=a[i+j],y=a[i+j+len]*g0%mod;a[i+j]=(x+y)%mod;a[i+j+len]=((x-y)%mod+mod)%mod;g0=g0*gn%mod;}}}
}
signed main() {int n=read();int k=get_read();int t=read();for(int i=1;i<=n;i++) {f[i]=read();}int limit=1,len=0;while(limit<=2*n) limit<<=1,len++;for(int i=0;i<=limit;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(len-1));g1[0]=1;for(int i=1;i<=n;i++) {g1[i]=g1[i-1]*(k+i-1)%mod*qpow(i,mod-2)%mod;}g2[0]=1;for(int i=1;i<=n;i++) {g2[i]=(g2[i-1]*(k-i+1)%mod*qpow(i,mod-2)%mod*-1+mod)%mod;}if(t==0) {NTT(f,limit,1);NTT(g1,limit,1);for(int i=0;i<=limit;i++) {f[i]=f[i]*g1[i]%mod;}NTT(f,limit,-1);int inv=qpow(limit,mod-2);for(int i=0;i<=limit;i++) {f[i]=f[i]*inv%mod;}}else {NTT(f,limit,1);NTT(g2,limit,1);for(int i=0;i<=limit;i++) {f[i]=f[i]*g2[i]%mod;}NTT(f,limit,-1);int inv=qpow(limit,mod-2);for(int i=0;i<=limit;i++) {f[i]=f[i]*inv%mod;}}for(int i=1;i<=n;i++) {cout<<f[i]<<" ";}return 0;
}
相关文章:

P5488 差分与前缀和
传送门:洛谷 前题提要:包含了简单的生成函数思想以及多项式乘法,是一道不可多得的多项式好题.故记录一下. 题意:给定一个长为 n 的序列 a,求出其 k 阶差分或前缀和。结果的每一项都需要对 1004535809取模。 对于差分和前缀和我们分开来讨论. 先讨论前缀和部分: …...

uboot启动流程-uboot内存分配
一. uboot启动流程 _main 函数中会调用 board_init_f 函数,本文继续简单分析一下 board_init_f 函数。 具体分析 board_init_f函数的第二部分:内存分配代码。 本文继上一篇文章的学习,地址如下: uboot启动流程-涉及board_init…...

LeetCode 面试题 08.02. 迷路的机器人
文章目录 一、题目二、C# 题解 一、题目 设想有个机器人坐在一个网格的左上角,网格 r 行 c 列。机器人只能向下或向右移动,但不能走到一些被禁止的网格(有障碍物)。设计一种算法,寻找机器人从左上角移动到右下角的路径…...
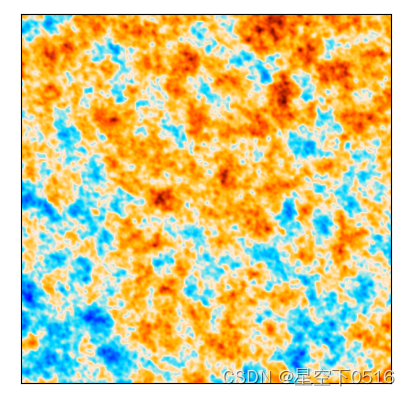
画CMB天图使用Planck配色方案
使用Planck的配色方案: 全天图: 或者方形图: 使用下面设置即可: import pspy, pixell from pspy.so_config import DEFAULT_DATA_DIR pixell.colorize.mpl_setdefault("planck")此方法不会改变matplotlib默认配色方案…...

成都瀚网科技有限公司:抖店精选联盟怎么用?
抖音精选联盟是抖音电商平台提供的一项服务,旨在为商家提供更多的推广机会和销售渠道。然而,很多人对于如何使用抖店精选联盟以及如何开通这项服务不太了解。本文将为您详细介绍抖店精选联盟的使用和激活流程。 第一节:如何使用抖店精选联盟 …...
)
第二章:最新版零基础学习 PYTHON 教程(第五节 - Python 输入/输出–如何在Python中打印而不换行?)
一般来说,从 C/C++ 切换到 Python 的人想知道如何在 python 中打印两个或多个变量或语句而不进入新行。由于Python print() 函数默认以换行符结尾。Python 有一个预定义的格式,如果你使用 print(a_variable) 那么它会自动转到下一行。 例子: # 输入:[csdn, csdnforcsdn] …...

C++实现集群聊天服务器
C实现集群聊天服务器 JSON Json是一种轻量级的数据交换模式(也叫做数据序列化方式)。Json采用完全独立于编程语言的文本格式来存储和表示数据。见解和清晰的层次结构使得Json称为理想的数据交换语言。易于阅读和编写。同时也易于支持机器解析和生成&am…...
40 二叉树的直径
二叉树的直径 总结:两个节点之间最长路径 路径的结点数 - 1题解1 递归——DFS 给你一棵二叉树的根节点,返回该树的 直径。 二叉树的直径是指树中任意两个节点之间最长路径的长度。这条路径可能经过也可能不经过根节点 root 。 两节点之间路径的长度由…...
的作用是什么?)
Thread.sleep(0)的作用是什么?
Thread.sleep(0) 的作用是让当前线程放弃剩余的时间片,允许其他具有相同优先级的线程运行。这种操作有时被称为“主动让出CPU时间片”或“线程主动让步”。 通常情况下,当一个线程执行到一段代码时,它会占用CPU的时间片,直到时间…...
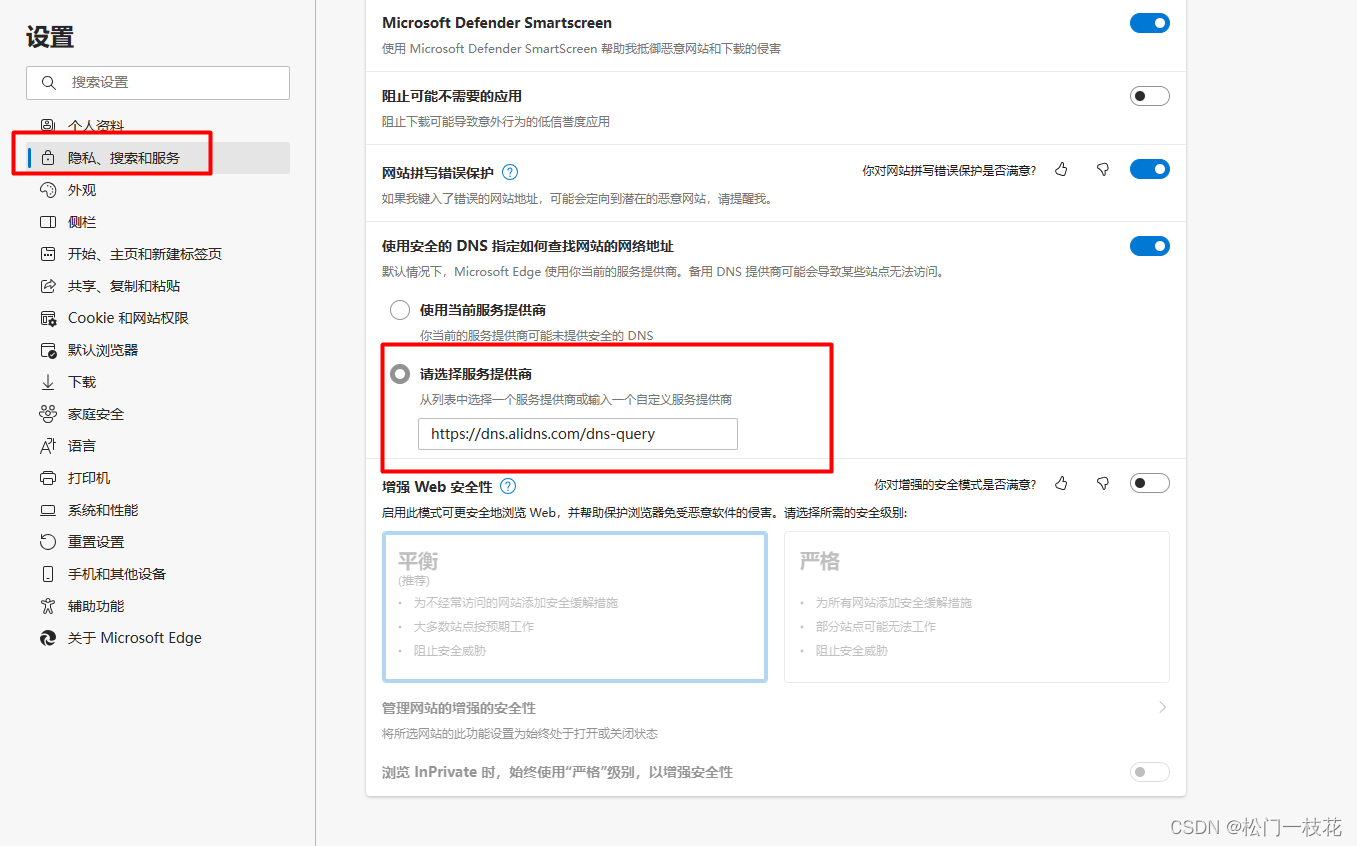
浏览器指定DNS
edge--设置 https://dns.alidns.com/dns-query...
虚拟机安装 centos
title: 虚拟机安装 centos createTime: 2020-12-13 12:00:27 updateTime: 2020-12-13 12:00:27 categories: linux tags: 虚拟机安装 centos 路线图 主机(宿主机) —> centos --> docker --> docker 镜像 --> docker 容器 — docker 服务 1.前期准备 一台 主机 或…...
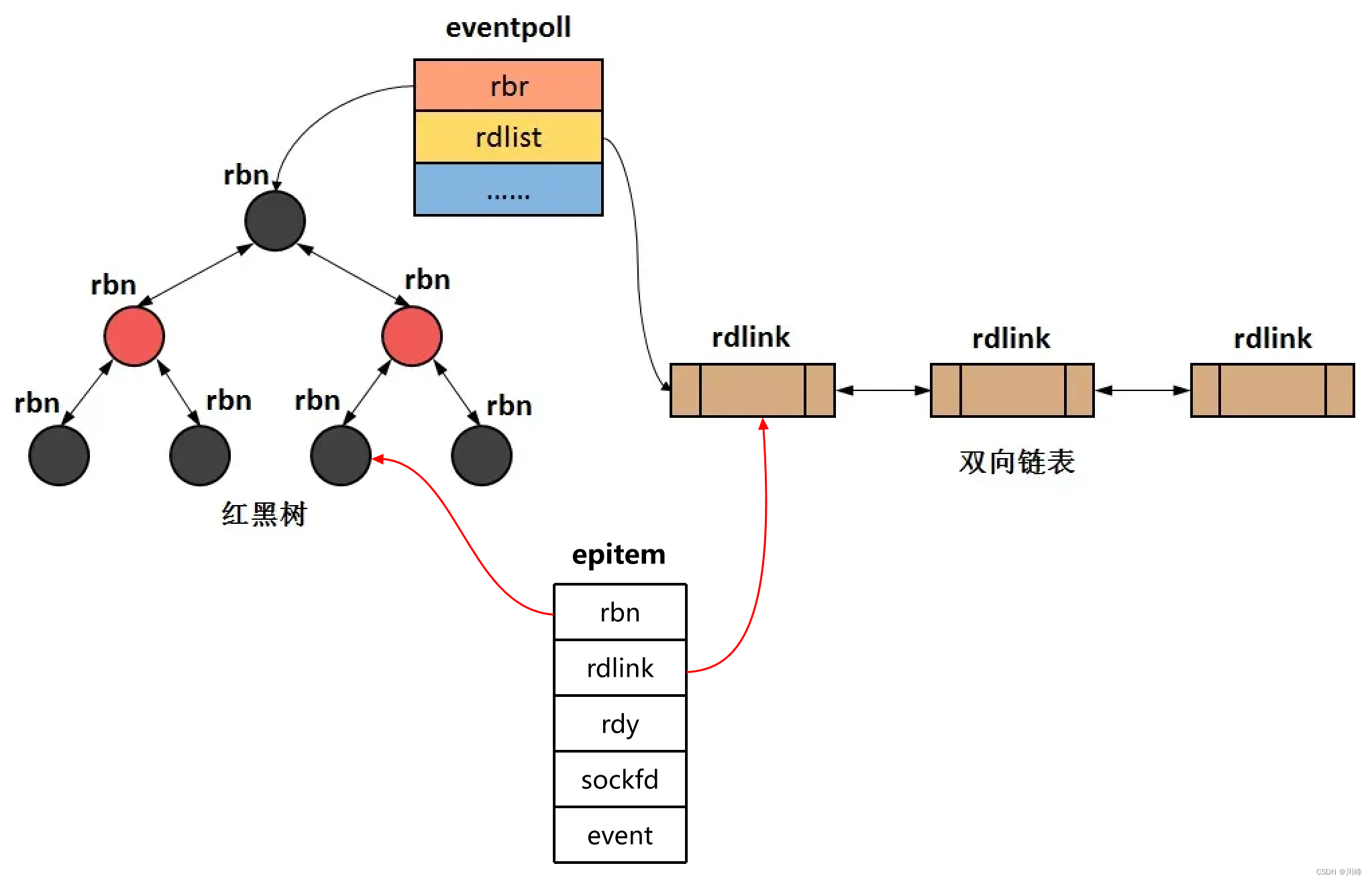
【计算机网络笔记九】I/O 多路复用
阻塞 IO 和 非阻塞 IO 阻塞 I/O 和 非阻塞 I/O 的主要区别: 阻塞 I/O 执行用户程序操作是同步的,调用线程会被阻塞挂起,会一直等待内核的 I/O 操作完成才返回用户进程,唤醒挂起线程非阻塞 I/O 执行用户程序操作是异步的…...

踩坑日记 《正确的使用Vuex》基于 uniapp Vue3 setup 语法糖 vuex4 项目 太多坑了要吐了
踩坑日记 《正确的使用Vuex》基于 uniapp Vue3 setup 语法糖 vuex4 项目 太多坑了要吐了 完美解决页面数据不刷新 或者数据慢一步刷新 页面使用html <template><view><template v-if"cartData.data.length>0"><!-- 自定义导航栏 --><…...

Python无废话-办公自动化Excel修改数据
如何修改Excel 符合条件的数据?用Python 几行代码搞定。 需求:将销售明细表的产品名称为PG手机、HW手机、HW电脑的零售价格分别修改为4500、5500、7500,并保存Excel文件。如下图 Python 修改Excel 数据,常见步骤: 1&…...

MySQL系统架构设计
MySQL 一、MySQL整体架构1.1 SQL接口1.2 解析器 Parser1.3 查询优化器 Optimizer1.3.1 逻辑优化1.3.2 物理优化1.3.3 explain1.4 缓存 Cache1.5 存储引擎 Stroage Management1.6 一条查询SQL的执行流程二、缓存池(Buffer Pool)2.1 Buffer Pool 预读机制2.2 Buffer Pool free链…...

Google vs IBM vs Microsoft: 哪个在线数据分析师证书最好
Google vs IBM vs Microsoft: 哪个在线数据分析师证书最好? 对目前市场上前三个数据分析师证书进行审查和比较|Madison Hunter 似乎每个重要的公司都推出了自己版本的同一事物:专业数据分析师认证,旨在使您成为雇主的下一个热门商品。 随着…...
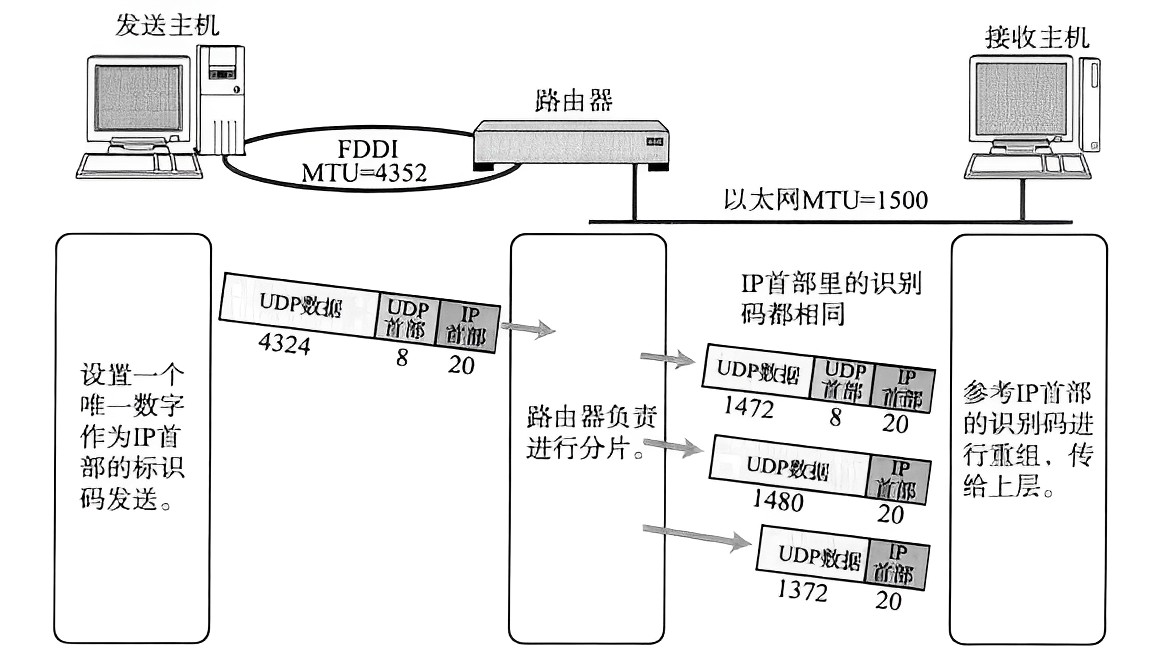
数据链路层 MTU 对 IP 协议的影响
在介绍主要内容之前,我们先来了解一下数据链路层中的"以太网" 。 “以太网”不是一种具体的网络,而是一种技术标准;既包含了数据链路层的内容,也包含了一些物理层的内容。 下面我们再来了解一下以太网数据帧ÿ…...
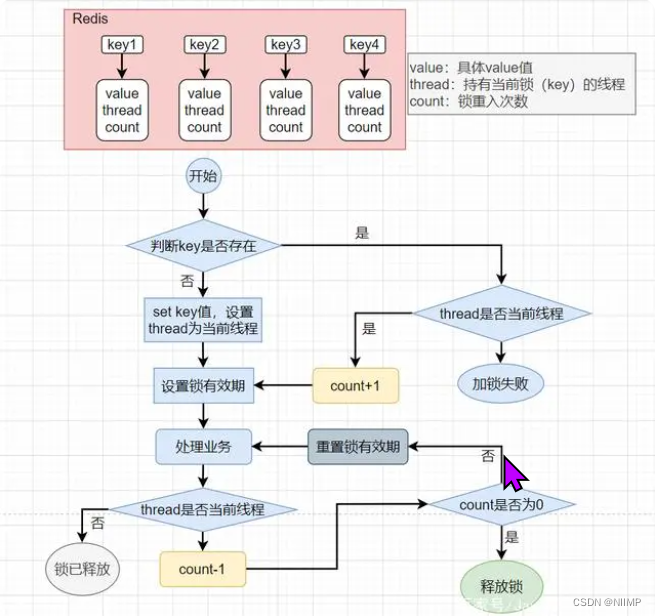
一文拿捏基于redis的分布式锁、lua、分布式性能提升
1.分布式锁 jdk的锁: 1、显示锁:Lock 2、隐式锁:synchronized 使用jdk锁保证线程的安全性要求:要求多个线程必须运行在同一个jvm中 但现在的系统基本都是分布式部署的,一个应用会被部署到多台服务器上,s…...

机器学习必修课 - 如何处理缺失数据
运行环境:Google Colab 处理缺失数据可简单分为两种方法:1. 删除具有缺失值的列 2. 填充 !git clone https://github.com/JeffereyWu/Housing-prices-data.git下载数据集 import pandas as pd from sklearn.model_selection import train_test_split导…...

阿里云服务器方升架构、自研硬件、AliFlash技术创新
阿里云服务器技术创新:服务器方升架构及自研硬件、自研存储硬件AliFlash和阿里云异构计算加速平台,阿里云百科分享阿里云服务器有哪些技术创新: 目录 服务器技术创新 服务器方升架构及自研硬件 自研存储硬件AliFlash 阿里云异构计算加速…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

LangChain【6】之输出解析器:结构化LLM响应的关键工具
文章目录 一 LangChain输出解析器概述1.1 什么是输出解析器?1.2 主要功能与工作原理1.3 常用解析器类型 二 主要输出解析器类型2.1 Pydantic/Json输出解析器2.2 结构化输出解析器2.3 列表解析器2.4 日期解析器2.5 Json输出解析器2.6 xml输出解析器 三 高级使用技巧3…...
