当前位置： 首页 > news >正文

深度学习笔记之线性代数

news 2026/2/10 3:43:47

深度学习笔记之线性代数

一、向量

在数学表示法中，向量通常记为粗体小写的符号（例如，x，y，z）当向量表示数据集中的样本时，它们的值具有一定的现实意义。例如研究医院患者可能面临的心脏病发作风险，用一个向量表示一个患者，其分量为最近的生命特征、胆固醇水平、每天运动时间等。
在这里插入图片描述
可以使用下标来引用向量的任意元素
在这里插入图片描述
使用切片访问
在这里插入图片描述
向量只是一个数字数组，就像每个数组都有一个长度，向量的长度通常称为向量的维度（dimension）
可以通过调用Python的内置len()函数来访问张量的长度
在这里插入图片描述

当张量表示一个向量时，可以通过.shape属性访问向量的长度。对于只有一个轴的张量，形状只有一个元素。
在这里插入图片描述

二、矩阵

矩阵将向量从一阶推广到二阶。通常用粗体大写字母表示矩阵（例如X，Y，Z），在代码中表示具有两个轴的张量。

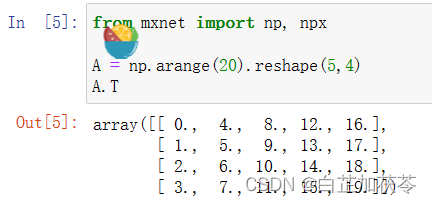
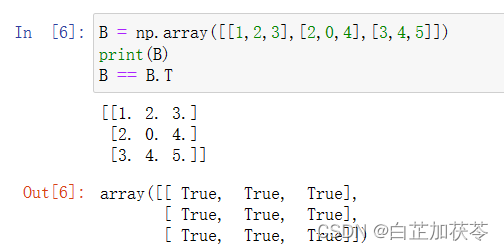
在这里插入图片描述
索引访问
在这里插入图片描述
求矩阵的转置
在这里插入图片描述
判断一个矩阵是否为对称矩阵。即这个矩阵是否等于它的转置矩阵。

在这里插入图片描述

三、张量算法的基本性质

两个形状相同的矩阵相加，会在这两个矩阵上执行元素加法
在这里插入图片描述
两个矩阵按元素乘法成为Hadamard积
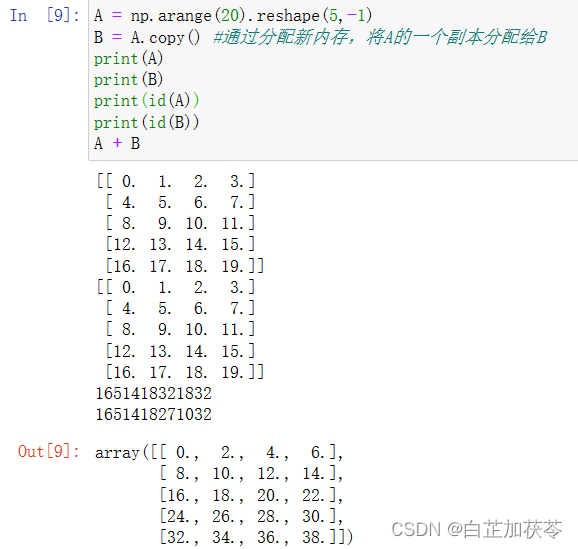
在这里插入图片描述
将张量乘以或加上一个标量不会改变张量的形状，其中张量的每个元素都与标量相加或相乘

在这里插入图片描述

四、降维

计算向量中元素的和
在这里插入图片描述

在这里插入图片描述

为了通过求和所有行元素来降维，可以在调用函数时制定axis=0
也可以指定axis=1将通过汇总所有列的元素降维
在这里插入图片描述
沿着行和列对矩阵求和，等价于对矩阵的所有元素进行求和
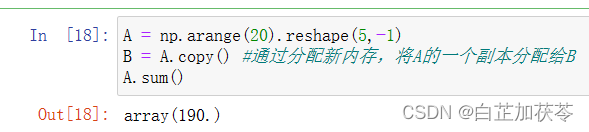
在这里插入图片描述

计算任意形状张量的平均值
在这里插入图片描述

五、非降维求和

在这里插入图片描述

如果我们想沿某个轴计算A元素的累积总和， 比如axis=0（按行计算），可以调用cumsum函数。 此函数不会沿任何轴降低输入张量的维度。

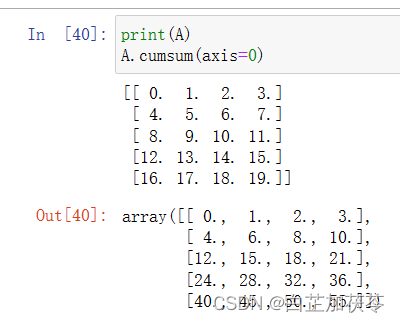
在这里插入图片描述

六、点积

在这里插入图片描述

七、矩阵-向量积

在这里插入图片描述

八、矩阵-矩阵乘法

在这里插入图片描述

九、范数

在这里插入图片描述
在这里插入图片描述

相关文章：

深度学习笔记之线性代数

深度学习笔记之线性代数 一、向量 在数学表示法中，向量通常记为粗体小写的符号（例如，x，y，z）当向量表示数据集中的样本时，它们的值具有一定的现实意义。例如研究医院患者可能面临的心脏病发作风…...

编程日记 2023/10/3 11:36:13

Python与Scrapy：构建强大的网络爬虫

网络爬虫是一种用于自动化获取互联网信息的工具，在数据采集和处理方面具有重要的作用。Python语言和Scrapy框架是构建强大网络爬虫的理想选择。本文将分享使用Python和Scrapy构建强大的网络爬虫的方法和技巧，帮助您快速入门并实现实际操作价值。 一、Pyt…...

编程日记 2023/10/3 11:34:11

kind 安装 k8s 集群

在某些时候可能需要快速的部署一个k8s集群用于测试，不想部署复杂的k8s集群环境，这个时候我们就可以使用kind来部署一个k8s集群了，下面是使用kind部署的过程 一、安装单节点集群 1、下载kind二进制文件 [rootlocalhost knid]# curl -Lo ./kin…...

编程日记 2023/10/3 11:29:06

Leetcode 2871. Split Array Into Maximum Number of Subarrays

Leetcode 2871. Split Array Into Maximum Number of Subarrays 1. 解题思路2. 代码实现 题目链接：2871. Split Array Into Maximum Number of Subarrays 1. 解题思路 这一题实现上其实还是比较简单的，就是一个贪婪算法，主要就是思路上需要…...

编程日记 2023/10/3 11:27:04

Java基础---第十三篇

系列文章目录 文章目录 系列文章目录一、有数组了为什么还要搞个 ArrayList 呢？二、说说什么是 fail-fast？三、说说Hashtable 与 HashMap 的区别一、有数组了为什么还要搞个 ArrayList 呢？ 通常我们在使用的时候，如果在不明确要插入多少数据的情况下，普通数组就很尴尬了，…...

编程日记 2023/10/3 11:26:03

Java 文档注释

Java 文档注释 目录 Java 文档注释 javadoc 标签 文档注释 javadoc输出什么 实例 Java只是三种注释方式。前两种分别是// 和/* */，第三种被称作说明注释，它以/** 开始，以 */结束。 说明注释允许你在程序中嵌入关于程序的信息。你可以使…...

编程日记 2023/10/3 11:25:02

【多媒体技术与实践】多媒体计算机系统概述

数码相机是利用___感受光信号， 使转换为电信号，再经模/数转换变成数字信号，存储在相机内部的存储器中。 选择一项： a. RGB b. OCR c. CCD d. MPEG 正确答案是：CCD 最基本的多媒体计算机是指安装了_部件的计算机。…...

编程日记 2023/10/3 11:22:00

DirectX 3D C++ 圆柱体的渲染（源代码）

作业内容 请勿抄袭 代码功能&#xff1a;渲染一个绕中心轴自转的圆柱体。要求该圆柱体高度为3.0&#xff0c;半径为0.5。 #include <windows.h> #include <d3d11.h> #include <d3dx11.h> #include <d3dcompiler.h> #include <xnamath.h> #incl…...

编程日记 2023/10/3 11:20:59

搭建前端框架

在终端进入web目录&#xff0c;然后创建vuecrud工程 创建工程并引入ElementUI和axios手把手教学>传送门:VueCLI脚手架搭建...

编程日记 2023/10/3 11:19:58

2310C++构造对象

原文 本文展示一个构造对象方式,用户无需显式调用构造器.对有参构造器类,该实现在构造改对象时传递默认值来构造. 当然用户也可指定(绑定)某个参数的值.实现思路参考boost-ext/di的实现.看下示例: 构 成员{整 x10; }; 构 成员1{整 x11; }; 类 例子1{ 公:例子1(成员 x,成员1 x…...

编程日记 2023/10/3 11:18:57

nginx多文件组织

背景&#xff1a; nginx的话&#xff0c;有时候&#xff0c;想部署多个配置&#xff0c;比如&#xff1a;使用不同的端口配置不同的web工程。 比如&#xff1a;8081部署&#xff1a;项目1的web页面。 8082部署&#xff1a;项目2的web页面。 1)nginx.conf worker_processes…...

编程日记 2023/10/3 11:13:53

扩容LVM卷导致lvm元数据丢失的恢复过程

一、问题描述 因某次MySQL binlog占用过高扩容时&#xff0c;是直接对云盘操作&#xff0c;而扩容直接操作了lvm卷而未操作云盘分区&#xff0c;并随后执行了扩容的partprobe&#xff0c;resize2fs卷等操作&#xff1b;最后&#xff0c;显示并未扩容成功&#xff0c;重启系统后…...

编程日记 2023/10/3 11:12:52

【MySQL教程】| （1-1） 2023MySQL-8.1.0 安装教程

文章目录 一、安装包下载二、安装配置1、解压安装包2、编写MySQL配置文件3、初始化MySQL数据库3、安装mysql服务并启动4、MySQL服务5、连接MySQL6、修改密码 三、配置环境变量四、防止mysql自启动拖慢开机时间 近日有粉丝问到mysql在win11的安装中遇到一些问题&#xff0c;应粉…...

编程日记 2023/10/3 11:09:49

数据大屏定时请求后端数据

需求&#xff1a; 因为大屏基本从上午展示到晚上&#xff0c;不会频繁去打开页面。 前端实现&#xff1a; 在Vue的created钩子函数中发送初次请求&#xff0c;并使用JavaScript中的setInterval函数来设置整点定时发送请求。以下是一个示例 <template><div><h1…...

编程日记 2023/10/3 11:07:47

数据结构--队列

一、队列是什么 队列是一种特殊的线性表&#xff0c;特殊之处在于它只允许在表的前端&#xff08;front&#xff09;进行删除操作&#xff0c;而在表的后端&#xff08;rear&#xff09;进行插入操作&#xff0c;队列是一种操作受限制的线性表。进行插入操作的端称为队尾&…...

编程日记 2023/10/3 11:06:46

Python绘图系统25：新增8种绘图函数

文章目录 常用绘图函数单选框的更改逻辑源代码 Python绘图系统&#xff1a; 前置源码&#xff1a; Python打造动态绘图系统&#x1f4c8;一 三维绘图系统 &#x1f4c8;二 多图绘制系统&#x1f4c8;三 坐 标 轴 定 制&#x1f4c8;四 定制绘图风格 &#x1f4c8;五 数据生成导…...

编程日记 2023/10/3 11:04:44

(二) gitblit用户使用教程

(一)gitblit安装教程 (二) gitblit用户使用教程 (三) gitblit管理员手册 目录 网页访问git客户端设置推送错误配置查看当前配置 日常使用仓库分组my profile修改上传代码简洁 网页访问 点击Advanced... 点击Accept the Risk and Contiue 初始用户名和密码都是admin,点击login…...

编程日记 2023/10/3 11:03:43

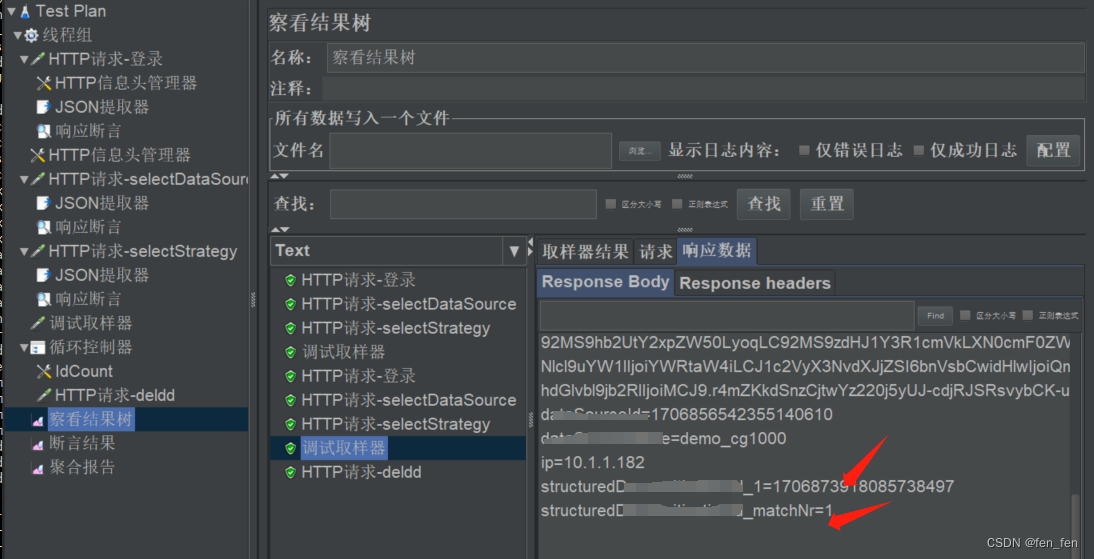
8.3Jmeter使用json提取器提取数组值并循环(循环控制器)遍历使用

Jmeter使用json提取器提取数组值并循环遍历使用 响应返回值例如&#xff1a; {"code":0,"data":{"totalCount":11,"pageSize":100,"totalPage":1,"currPage":1,"list":[{"structuredId":&q…...

编程日记 2023/10/3 11:02:42

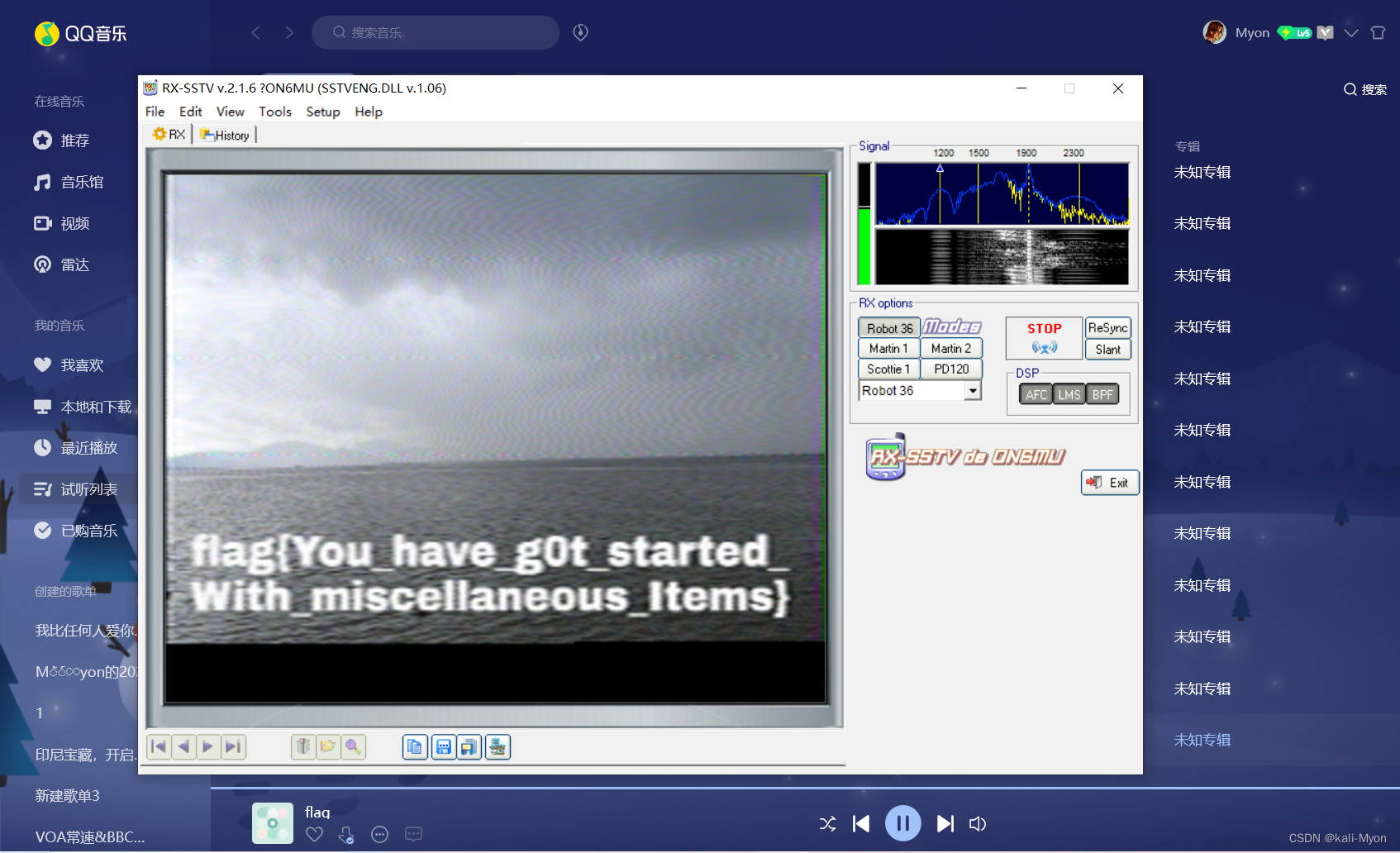
SNERT预备队招新CTF体验赛-Misc（SWCTF）

目录 1、最简单的隐写 2、旋转我 3、is_here 4、zip伪加密 5、压缩包密码爆破 6、我就藏在照片里 7、所以我放弃了bk 8、套娃 9、来自银河的信号 10、Track_Me 11、勇师傅的奇思妙想 1、最简单的隐写 下载附件后&#xff0c;图片格式并不支持打开 根据题目提示&…...

编程日记 2023/10/3 11:00:40

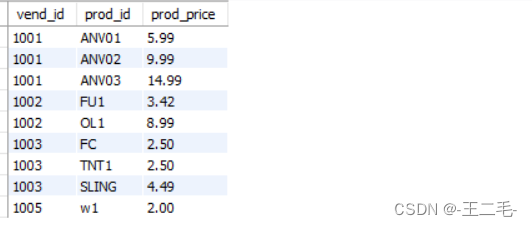
MySql017——组合查询

一、UNION作用 可用UNION操作符来组合数条SQL查询。 二、UNION 使用规则 1、UNION的使用很简单。所需做的只是给出每条SELECT语句&#xff0c;在各条语句之间放上关键字UNION。2、UNION必须由两条或两条以上的SELECT语句组成&#xff0c;语句之间用关键字UNION分隔&#xff…...

编程日记 2023/10/3 10:57:36

云原生核心技术 (7/12): K8s 核心概念白话解读(上)：Pod 和 Deployment 究竟是什么？

大家好&#xff0c;欢迎来到《云原生核心技术》系列的第七篇&#xff01; 在上一篇&#xff0c;我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在&#xff0c;我们就像一个拥有了一块崭新数字土地的农场主&#xff0c;是时…...

编程新知 2025/12/14 22:32:59

Cursor实现用excel数据填充word模版的方法

cursor主页&#xff1a;https://www.cursor.com/ 任务目标&#xff1a;把excel格式的数据里的单元格&#xff0c;按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例&#xff0c;…...

编程新知 2025/8/23 5:46:26

unix/linux，sudo，其发展历程详细时间线、由来、历史背景

sudo 的诞生和演化，本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来，让我们拨开时间的迷雾，一同探寻 sudo 那波澜壮阔（也颇为实用主义）的发展历程。 历史背景：su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前，Unix 系统管理员和需要特权操作的…...

编程新知 2025/11/18 21:31:41

三体问题详解

从物理学角度&#xff0c;三体问题之所以不稳定&#xff0c;是因为三个天体在万有引力作用下相互作用&#xff0c;形成一个非线性耦合系统。我们可以从牛顿经典力学出发&#xff0c;列出具体的运动方程&#xff0c;并说明为何这个系统本质上是混沌的&#xff0c;无法得到一般解…...

编程新知 2025/10/19 5:14:05

Linux --进程控制

本文从以下五个方面来初步认识进程控制&#xff1a; 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程&#xff0c;创建出来的进程就是子进程&#xff0c;原来的进程为父进程。…...

编程新知 2026/1/30 15:27:25

纯 Java 项目（非 SpringBoot）集成 Mybatis-Plus 和 Mybatis-Plus-Join

纯 Java 项目&#xff08;非 SpringBoot&#xff09;集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

编程新知 2025/9/26 12:26:35

Python网页自动化Selenium中文文档

1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API&#xff0c;让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API&#xff0c;你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...

编程新知 2026/1/23 18:15:21

【FTP】ftp文件传输会丢包吗？批量几百个文件传输，有一些文件没有传输完整，如何解决？

FTP&#xff08;File Transfer Protocol&#xff09;本身是一个基于 TCP 的协议&#xff0c;理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况&#xff0c;主要原因包括&#xff1a; ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...

编程新知 2025/8/17 3:31:21

一些实用的chrome扩展0x01

简介 浏览器扩展程序有助于自动化任务、查找隐藏的漏洞、隐藏自身痕迹。以下列出了一些必备扩展程序&#xff0c;无论是测试应用程序、搜寻漏洞还是收集情报&#xff0c;它们都能提升工作流程。 FoxyProxy 代理管理工具&#xff0c;此扩展简化了使用代理&#xff08;如 Burp…...

编程新知 2026/2/4 17:28:54

算法250609 高精度

加法 #include<stdio.h> #include<iostream> #include<string.h> #include<math.h> #include<algorithm> using namespace std; char input1[205]; char input2[205]; int main(){while(scanf("%s%s",input1,input2)!EOF){int a[205]…...

编程新知 2025/9/17 10:04:40