通过连接另一个数组的子数组得到一个数组
给你一个长度为 n 的二维整数数组 groups ,同时给你一个整数数组 nums 。
你是否可以从 nums 中选出 n 个 不相交 的子数组,使得第 i 个子数组与 groups[i] (下标从 0 开始)完全相同,且如果 i > 0 ,那么第 (i-1) 个子数组在 nums 中出现的位置在第 i 个子数组前面。(也就是说,这些子数组在 nums 中出现的顺序需要与 groups 顺序相同)
如果你可以找出这样的 n 个子数组,请你返回 true ,否则返回 false 。
如果不存在下标为 k 的元素 nums[k] 属于不止一个子数组,就称这些子数组是 不相交 的。子数组指的是原数组中连续元素组成的一个序列。
示例 1:
输入: groups = [[1,-1,-1],[3,-2,0]], nums = [1,-1,0,1,-1,-1,3,-2,0]> 输出: true> 解释: 你可以分别在 nums 中选出第 0 个子数组 [1,-1,0,1,-1,-1,3,-2,0] 和第 1 个子数组 [1,-1,0,1,-1,-1,3,****-2,0] 。> 这两个子数组是不相交的,因为它们没有任何共同的元素。
示例 2:
输入: groups = [[10,-2],[1,2,3,4]], nums = [1,2,3,4,10,-2]> 输出: false> 解释: 选择子数组 [1,2,3,4,10,-2] 和 [1,2,3,4,10,-2] 是不正确的,因为它们出现的顺序与 groups 中顺序不同。> [10,-2] 必须出现在 [1,2,3,4] 之前。
示例 3:
输入: groups = [[1,2,3],[3,4]], nums = [7,7,1,2,3,4,7,7]> 输出: false> 解释: 选择子数组 [7,7,1,2,3,4,7,7] 和 [7,7,1,2,3,4,7,7] 是不正确的,因为它们不是不相交子数组。> 它们有一个共同的元素 nums[4] (下标从 0 开始)。
提示:
groups.length == n1 <= n <= 10^31 <= groups[i].length, sum(groups[i].length) <= 10^31 <= nums.length <= 10^3-10^7 <= groups[i][j], nums[k] <= 10^7
思路
本题可以使用双指针遍历求解。我们用i作为下标遍历nums,用j作为下标遍历groups,设groups[j]的长度为n,我们需要比较以nums[i]到nums[i + n - 1]是否和groups[j]中每个元素都相等,
- 如果相等,
i = i + n,j = j + 1 - 如果不相等,
i = i + 1
进行同样的比较直到nums遍历完或groups遍历完,如果groups遍历完,返回true,否则返回false,代码如下。
解题
/*** @param {number[][]} groups* @param {number[]} nums* @return {boolean}*/
var canChoose = function (groups, nums) {const m = groups.length;const n = nums.length;let i = 0;let j = 0;while (i < n && j < m) {let k = 0;while (k < groups[j].length) {if (groups[j][k] !== nums[i + k]) {break;} else {k++;}}if (k === groups[j].length) {i += groups[j].length;j++;} else {i++;}}return j === m;
};
最后
最近还整理一份JavaScript与ES的笔记,一共25个重要的知识点,对每个知识点都进行了讲解和分析。能帮你快速掌握JavaScript与ES的相关知识,提升工作效率。



有需要的小伙伴,可以点击下方卡片领取,无偿分享
相关文章:

通过连接另一个数组的子数组得到一个数组
给你一个长度为 n 的二维整数数组 groups ,同时给你一个整数数组 nums 。 你是否可以从 nums 中选出 n 个 不相交 的子数组,使得第 i 个子数组与 groups[i] (下标从 0 开始)完全相同,且如果 i > 0 ,那么…...

公派访问学者的申请条件
知识人网海外访问学者申请老师为大家分享公派访问学者申请的基本条件以及哪些人员的申请是暂不受理的,供大家参考:一、 申请人基本条件:1.热爱社会主义祖国,具有良好的思想品德和政治素质,无违法违纪记录。2.具有良好专…...
多点电容触摸屏实验
目录 一、简介 二、硬件原理 编辑1、CT_INT 2、I2C2_SCL和I2C2_SDA 3、RESET复位引脚 三、FT54x6/FT52x6电容触摸芯片 四、代码编写 1、编写ft5426.h 2、编写ft5426.c 3、main函数 一、简介 电容屏只需要手指轻触即可,而电阻屏是需要手指给予一定的压力才…...

【算法与数据结构(C语言)】栈和队列
文章目录 目录 前言 一、栈 1.栈的概念及结构 2.栈的实现 入栈 出栈 获取栈顶元素 获取栈中有效元素个数 检测栈是否为空,如果为空返回非零结果,如果不为空返回0 销毁栈 二、队列 1.队列的概念及结构 2.队列的实现 初始化队列 队尾入队列 队头出队列 获…...
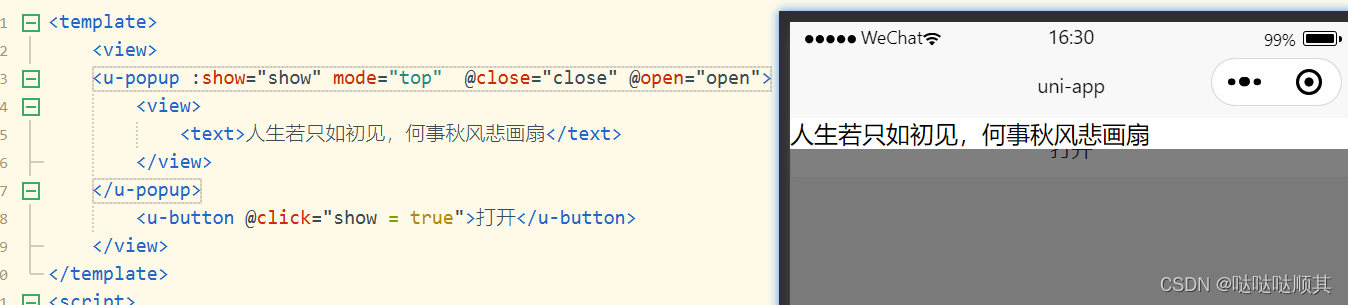
Uni-app使用vant和uview组件
目录 1.安装vant组件 1.1安装前需知 1.2.安装 1.3.创建uni-app项目 2.安装uview-ui组件 2.1官网 2.2安装 2.3安装成功 1.安装vant组件 1.1安装前需知 小程序能使用vant-weapp组件,且官网的安装是直接导入小程序中,不能直接导入uni-app框架中 V…...
2023年PMP考试应该注意些什么?
首先注意(报考条件) 2023年PMP考试报名流程: 一、PMP英文报名: 英文报名时间无限制,随时可以报名,但有一年的有效期,所以大家尽量提前报名,在英文报名有效期内进行中文报名。 英…...
selenium环境安装及使用
selenium简介官网https://www.selenium.dev简介用于web浏览器测试的工具支持的浏览器包括IE,Firefox,Chrome,edge等使用简单,可使用java,python等多种语言编写用例脚本主要由三个工具构成,webdriver,IDE,web自动化环境…...
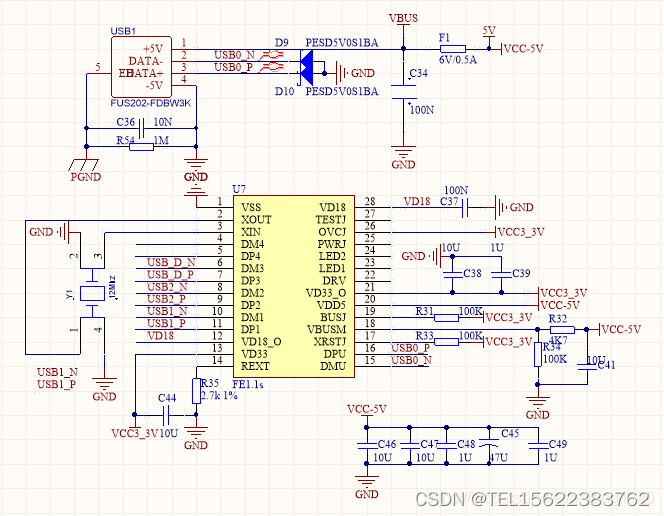
高性能低功耗4口高速USB2.0 HUB 完美替代FE1.1S和FE8.1
该NS1.1s是一个高度集成的,高品质,高性能,低功耗,为USB 2.0高速4端口集线器又低成本的解决方案。 (点击即可咨询芯片详细信息) NS1.1s的特点 1.通用串行总线规范修订版2.0(USB 2.0)完…...
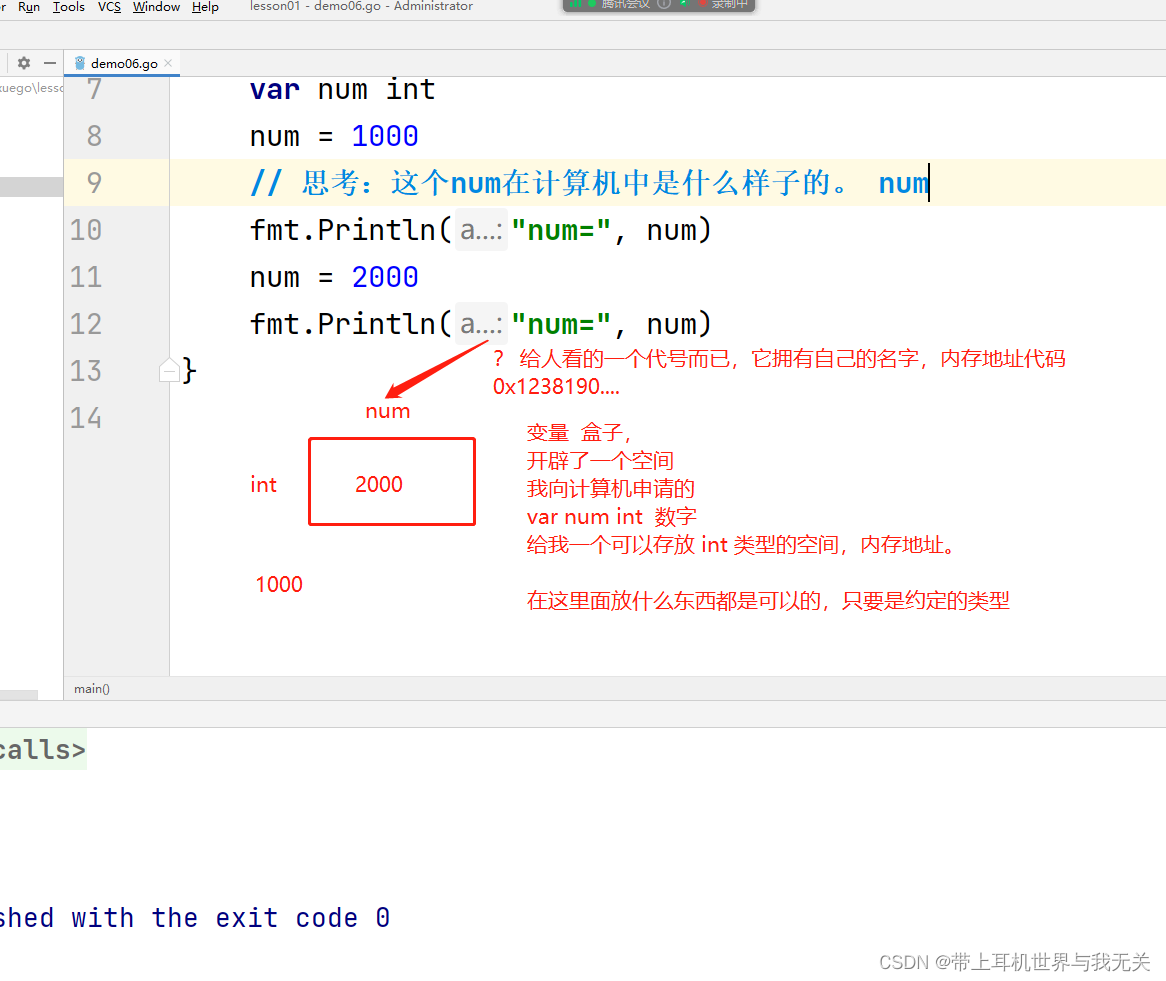
Go全栈学习(一)基础语法
Go语言基础语法 文章目录Go语言基础语法注释变量变量的定义变量的交换理解变量(内存地址)匿名变量变量的作用域常量2023.2.4日 总结// 关于Goland 中 执行的问题// 1、包下执行 (一个 main 函数来执行,如果有多个,无法…...
centos7搭建svn配置
基本概述 Apache Subversion(简称SVN,svn),一个开放源代码的版本控制系统,相较于RCS、CVS,它采用了分支管理系统,它的设计目标就是取代CVS。互联网上很多版本控制服务已从CVS转移到Subversion。…...
趣味三角——第12章——tanx
第12章节 tanx In his very numerous memoires, and especially in his great work, Introductio in analysin infinitorum (1748), Euler displayed the most wonderful skill in obtaining a rich harvest of results of great interest. . . . Hardly any other work …...
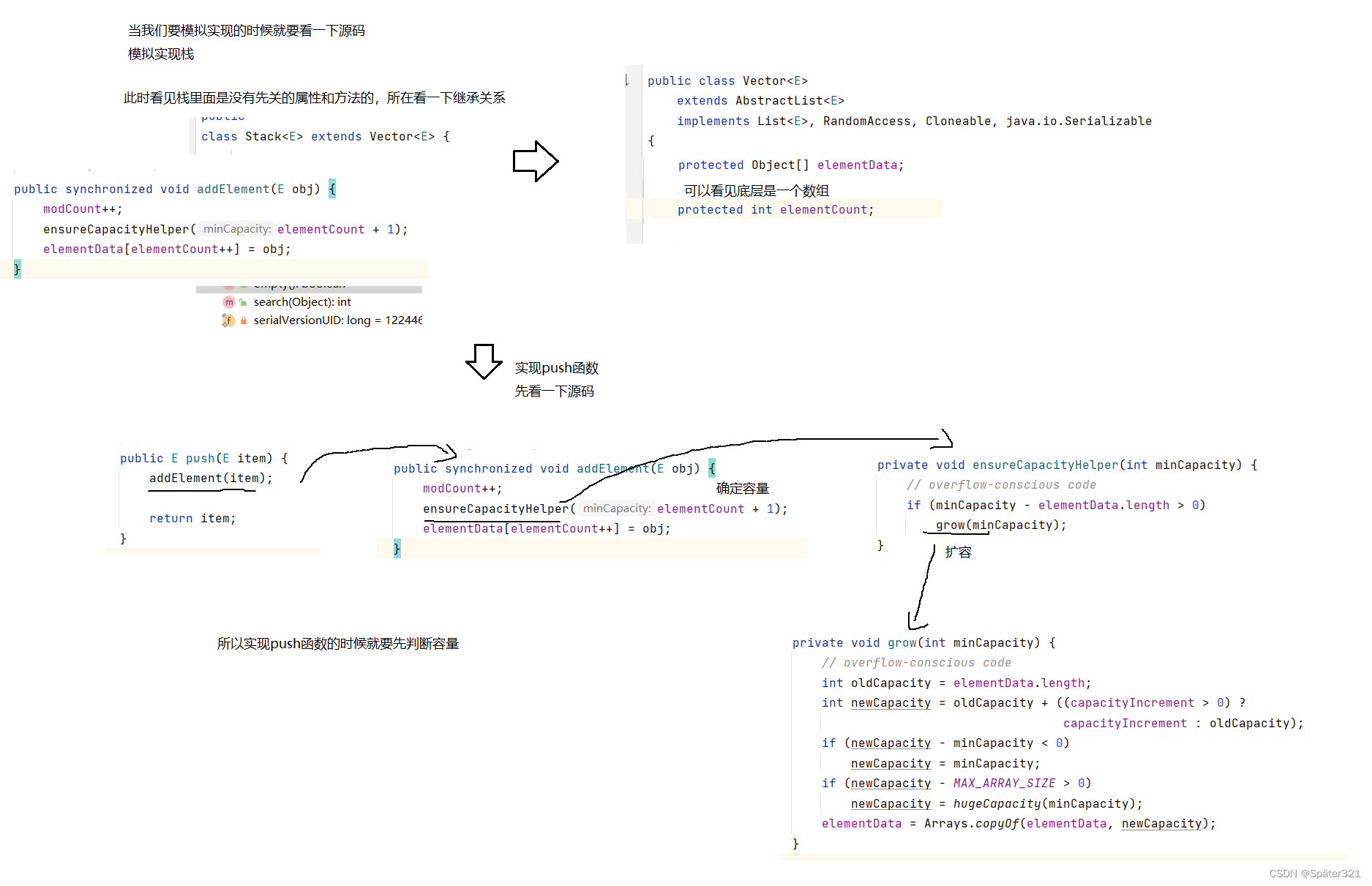
Java - 数据结构,栈
一、栈 1.1、什么是栈 栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈 顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。 压…...
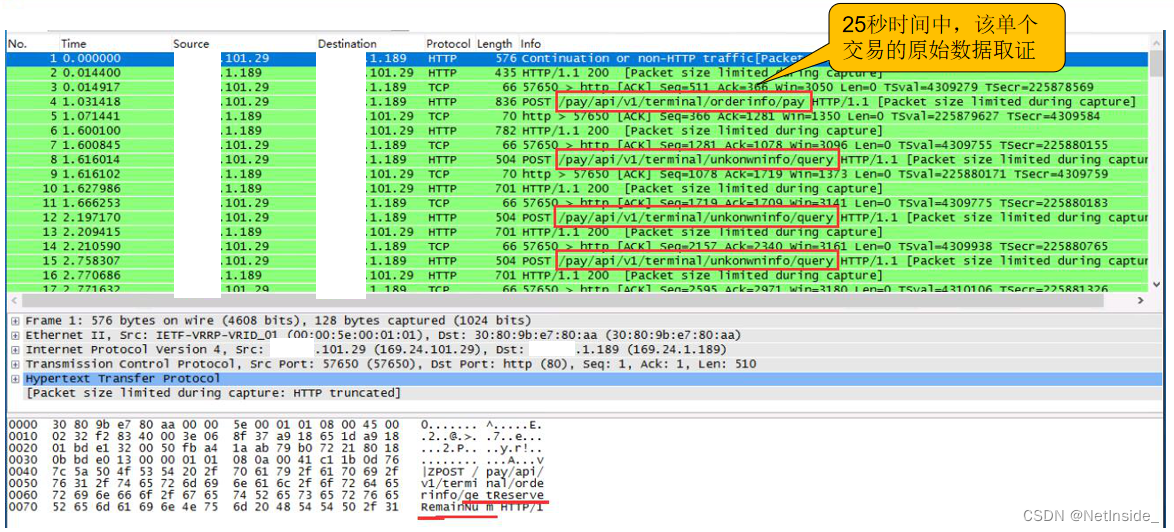
某餐厅系统网络故障分析案例
背景 针对食堂经营企业,某堂食软件为客户提供优化堂食就餐流程、提高食堂服务水平和管理效率。 某上海客户使用该堂食系统,在就餐高峰时段,总是出现支付、点餐等操作缓慢,动辄一个操作需要等待几十秒。该客户联系软件厂商&#…...

华为OD机试题,用 Java 解【密室逃生游戏】问题
最近更新的博客 华为OD机试 - 猴子爬山 | 机试题算法思路 【2023】华为OD机试 - 分糖果(Java) | 机试题算法思路 【2023】华为OD机试 - 非严格递增连续数字序列 | 机试题算法思路 【2023】华为OD机试 - 消消乐游戏(Java) | 机试题算法思路 【2023】华为OD机试 - 组成最大数…...

如何重命名SQL Server数据库
重命名SQL Server数据库 使用T-SQL重命名SQL Server数据库使用分离和附加重命名SQL Server数据库使用T-SQL查询分离和重新连接在SSMS中分离和重新连接通过SSMS重命名SQL Server数据库当使用SQL数据库很长一段时间时,你可能会遇到需要为数据库命名的情况。它可以用几种不同的方…...

联想昭阳E5-ITL电脑开机后绿屏怎么U盘重装系统?
联想昭阳E5-ITL电脑开机后绿屏怎么U盘重装系统?有用户电脑正常开机之后,出现了屏幕变成绿屏,无法进行操作的情况。这个问题是系统出现了问题,那么如何去进行问题的解决呢?接下来我们一起来分享看看如何使用U盘重装电脑…...
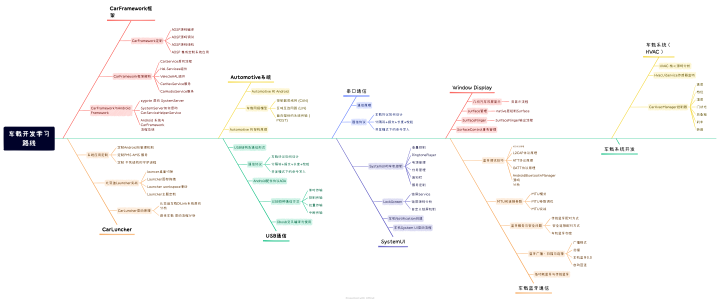
车载开发知识交流【学习路线】
前言 在2023国内百废待兴;经济复苏的号召一直在响应,这对于压抑了三年的人民来说无疑是福音。这篇我们主要说一下拉动经济的其中大板块——车企;我们知道我们最大的经济除了房地产,第二就是车企。而在造车领域中也不断的加入了许…...

【读书笔记】《深入浅出数据分析》第二章 检验你的理论
文章目录一,相关分析方法1,相关系数二,相关性不等于因果关系三,证明因果关系,“控制变量法”?本章主要说明了两个问题: 1,相关性不等于因果关系 2,如何判断两种数据之间是相关性&am…...
:table_apisql)
pyflink学习笔记(一):table_apisql
具体定义请参考官方文档:https://nightlies.apache.org/flink/flink-docs-release-1.16/zh/docs/dev/table/overview/本文主要针对实际使用中比较常用的api进行整理,大多数例子都是官网,如有歧义可与官方对照。一、 创建 TableEnvironmentTab…...

GCC 编译器套件说明
写在前面: 本文章旨在总结备份、方便以后查询,由于是个人总结,如有不对,欢迎指正;另外,内容大部分来自网络、书籍、和各类手册,如若侵权请告知,马上删帖致歉。 目录GCC 简述GCC 主要…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...
