Unity实现设计模式——状态模式
Unity实现设计模式——状态模式
状态模式最核心的设计思路就是将对象的状态抽象出一个接口,然后根据它的不同状态封装其行为,这样就可以实现状态和行为的绑定,最终实现对象和状态的有效解耦。
在实际开发中一般用到FSM有限状态机的实现,GF框架中的FSM和流程控制就是基于这个原理实现的。
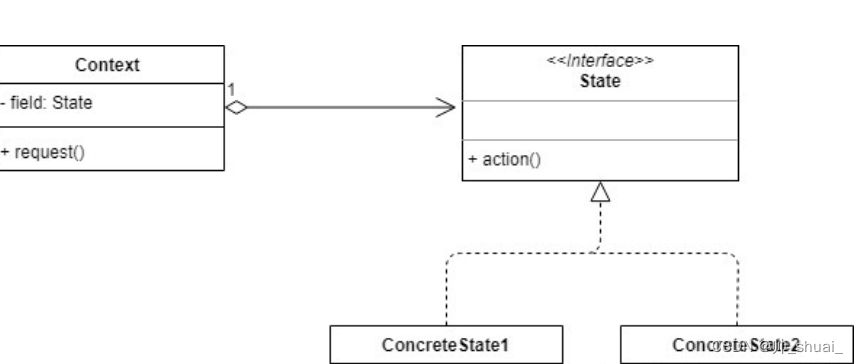
1.State(状态的抽象基类)
public abstract class State{protected Context m_Context = null;public State(Context theContext){m_Context = theContext;}public abstract void Handle(int Value);}
2.ConcreteStateA,ConcreteStateB,ConcreteStateC
状态State的子类
/// <summary>/// 状态A/// </summary>public class ConcreteStateA : State{public ConcreteStateA(Context theContext) : base(theContext){ }public override void Handle(int Value){Debug.Log("ConcreteStateA.Handle");if (Value > 10)m_Context.SetState(new ConcreteStateB(m_Context));}}/// <summary>/// 状态B/// </summary>public class ConcreteStateB : State{public ConcreteStateB(Context theContext) : base(theContext){ }public override void Handle(int Value){Debug.Log("ConcreteStateB.Handle");if (Value > 20)m_Context.SetState(new ConcreteStateC(m_Context));}}/// <summary>/// 状态C/// </summary>public class ConcreteStateC : State{public ConcreteStateC(Context theContext) : base(theContext){ }public override void Handle(int Value){Debug.Log("ConcreteStateC.Handle");if (Value > 30)m_Context.SetState(new ConcreteStateA(m_Context));}}
3.Context
Context类-持有目前的状态,并将相关信息传给状态
public class Context{State m_State = null;public void Request(int Value){m_State.Handle(Value);}public void SetState(State theState){Debug.Log("Context.SetState:" + theState);m_State = theState;}}
4.测试代码
public class StatePatternExample5 : MonoBehaviour{void Start(){UnitTest();}void UnitTest(){Context theContext = new Context();theContext.SetState(new ConcreteStateA(theContext));theContext.Request(5);theContext.Request(15);theContext.Request(25);theContext.Request(35);}}
相关文章:

Unity实现设计模式——状态模式
Unity实现设计模式——状态模式 状态模式最核心的设计思路就是将对象的状态抽象出一个接口,然后根据它的不同状态封装其行为,这样就可以实现状态和行为的绑定,最终实现对象和状态的有效解耦。 在实际开发中一般用到FSM有限状态机的实现&…...

差分数组的应用技巧
前缀和技巧 针对的算法场景是不需要对原始数组进行修改的情况下,频繁查询某个区间的累加和。 差分数组 主要适用场景是频繁对原始数组的某个区间的元素进行增减。 相关题目 1094. 拼车 1109. 航班预订统计 370. 区间加法 # 1094. 拼车 class Solution:def carPool…...
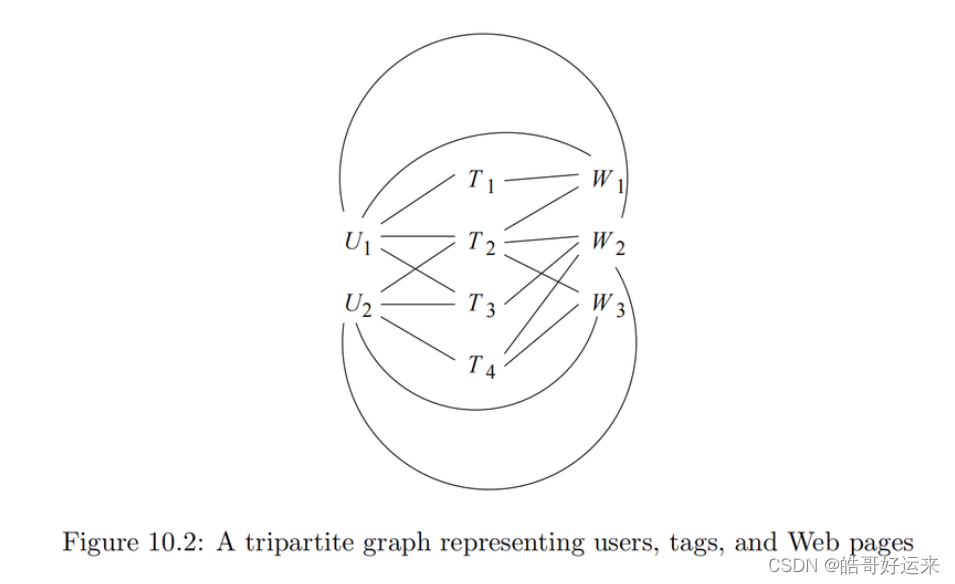
斯坦福数据挖掘教程·第三版》读书笔记(英文版)Chapter 10 Mining Social-Network Graphs
来源:《斯坦福数据挖掘教程第三版》对应的公开英文书和PPT。 Chapter 10 Mining Social-Network Graphs The essential characteristics of a social network are: There is a collection of entities that participate in the network. Typically, these entiti…...

DFS:842. 排列数字
给定一个整数 nn,将数字 1∼n1∼n 排成一排,将会有很多种排列方法。 现在,请你按照字典序将所有的排列方法输出。 输入格式 共一行,包含一个整数 nn。 输出格式 按字典序输出所有排列方案,每个方案占一行。 数据…...

pytorch之nn.Conv1d详解
自然语言处理中一个句子序列,一维的,所以使用Conv1d...

H5生成二维码
H5生成二维码: 1.引入js库,可自行点击链接复制使用 <script type"text/javascript" src"http://static.runoob.com/assets/qrcode/qrcode.min.js"></script>2.加入二维码占位区HTML <div id"qrCode">…...

Three.js加载360全景图片/视频
Three.js加载360全景图片/视频 效果 原理 将全景图片/视频作为texture引入到three.js场景中将贴图与球形网格模型融合,将球模型当做成环境容器使用处理视频时需要以dom为载体,加载与控制视频动作每次渲染时更新当前texture,以达到视频播放效…...

北大硕士7年嵌入式学习经验分享
阶段 1 大一到大三这个阶段我与大多数学生相同: 学习本专业知识(EE专业),学习嵌入式软件开发需要的计算机课程(汇编原理,计算机组成原理,操作系统,C语言等),…...

华为鸿蒙手表开发之动态生成二维码
华为鸿蒙手表开发之动态生成二维码 前言: 最近入职新公司,由于之前的哥们临时离职,走得很突然,所以没有任何交接和文档,临时顶上公司手表应用的上架,更换了新的密钥和key之后重新测试功能和流程ÿ…...
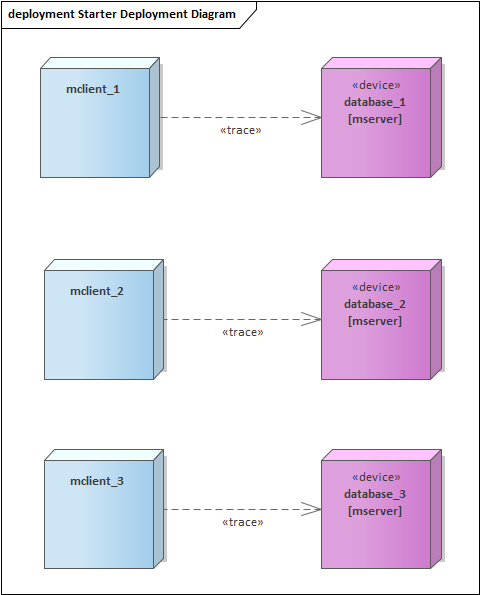
2023-09-28 monetdb-databae的概念和作用-分析
摘要: 每个数据库对于db,schema以及user,role都有一套自己的设计, 不同数据库间对于相同名字的东西例如database和schema可以说南辕北辙, 例如mysql中schema其实是database的同义词. 本文分析monetdb的database的概念和作用 database的概念和作用: 和mysql的database完全不同…...

2024级199管理类联考之数学基础(上篇)
管理类考试介绍 管理综合200分,时间3小时 数学:75分/25题,是拉开差距的核心模块 问题求解题:15个,5选一条件充分性判断:10个,结合两个条件选择答案 条件一充分,条件二不充分:A条件一不充分,条件二充分:B条件一充分,条…...
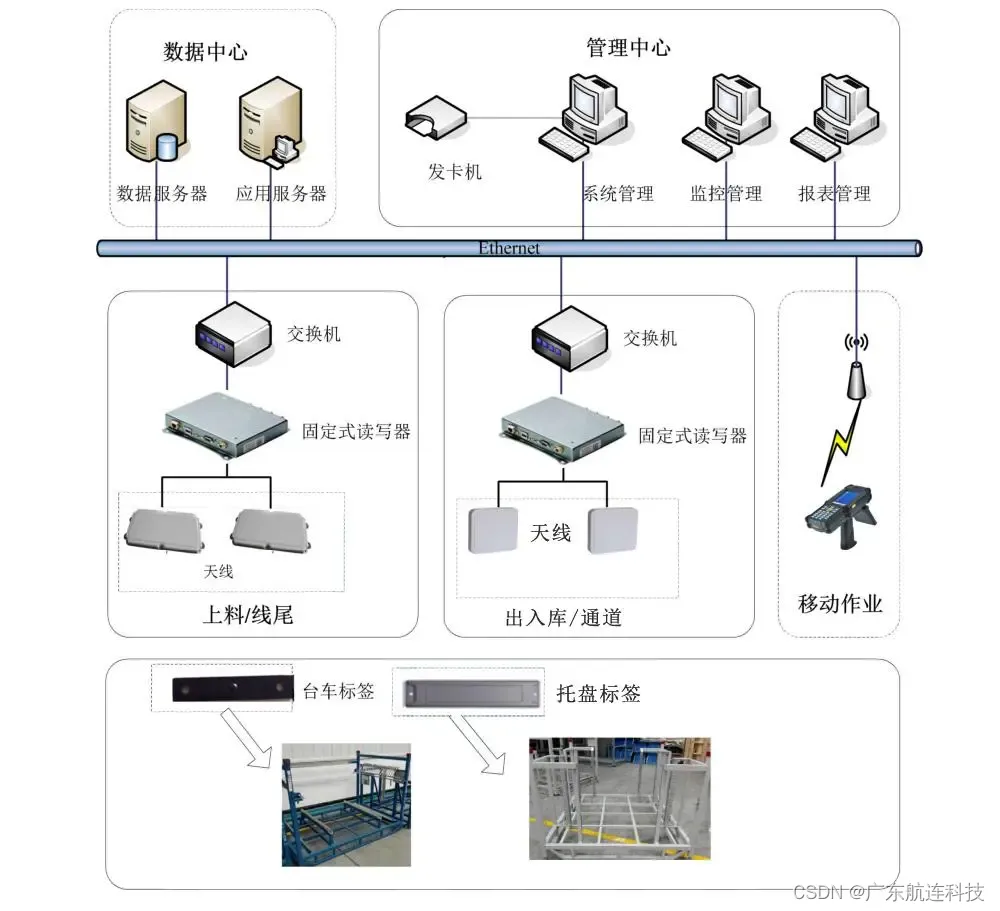
RFID技术引领汽车零部件加工新时代
RFID技术的兴起引领了汽车零部件加工领域的新时代,作为一种利用无线电频率进行自动识别的技术,RFID技术能够快速、准确地识别物体并获取相关数据,在汽车零部件加工中,RFID技术具有重要的应用价值,可以提高生产效率、降…...
python中使用matplotlib绘图
一、背景 当我们在写python程序时,不可避免的需要将数据可视化,也就是绘制出数据的曲线图,以便我们更直观的观察数据间的变化,和方便对比。此时就要用到matplotlib库了。 matplotlib官方给出的定义是: 翻译过来也就是…...

Qt Creator 使用技巧
使用技巧 功能快捷键解释Switch Header/SourceF4在同名的头文件和源程序文件之间切换Follow Symbol Under CursorF2变量:跳转到声明;函数:声明和定义切换Refactor Rename Symbol Under CursorCtrlShiftR改名称,将替换所有用到这个符号的地方RefactorAdd Definition…...

来看看双阶段目标检测算法趴
🚀 作者 :“码上有钱” 🚀 文章简介 :AI-目标检测算法 🚀 欢迎小伙伴们 点赞👍、收藏⭐、留言💬简介 双阶段目标检测算法是一类深度学习算法,通常分为两个阶段来检测和识别图像中的…...
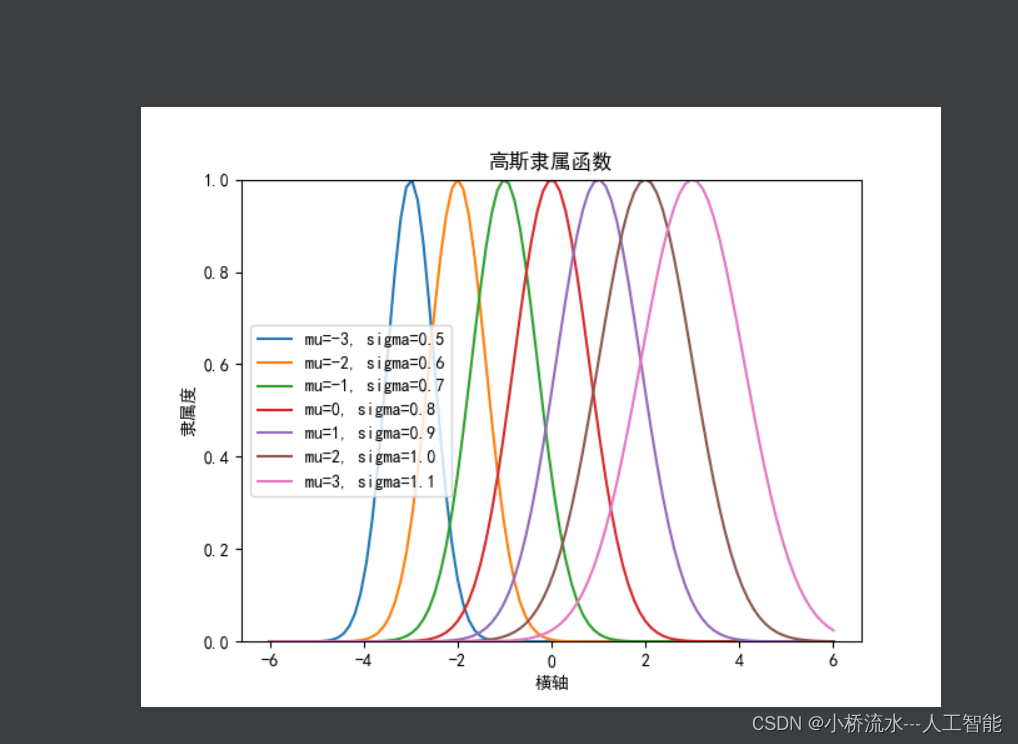
python利用matplotlib绘图,对于中文和负号不显示,显示方框“口口”完美解决办法!!
文章目录 一、问题展示二、问题分析三、解决办法四、结果展示 一、问题展示 二、问题分析 可以发现对中文,以及负号不显示。 三、解决办法 import matplotlib.pyplot as pltplt.rcParams[font.sans-serif] [usimHei] # 显示中文 plt.rcParams[axes.unicode_mi…...
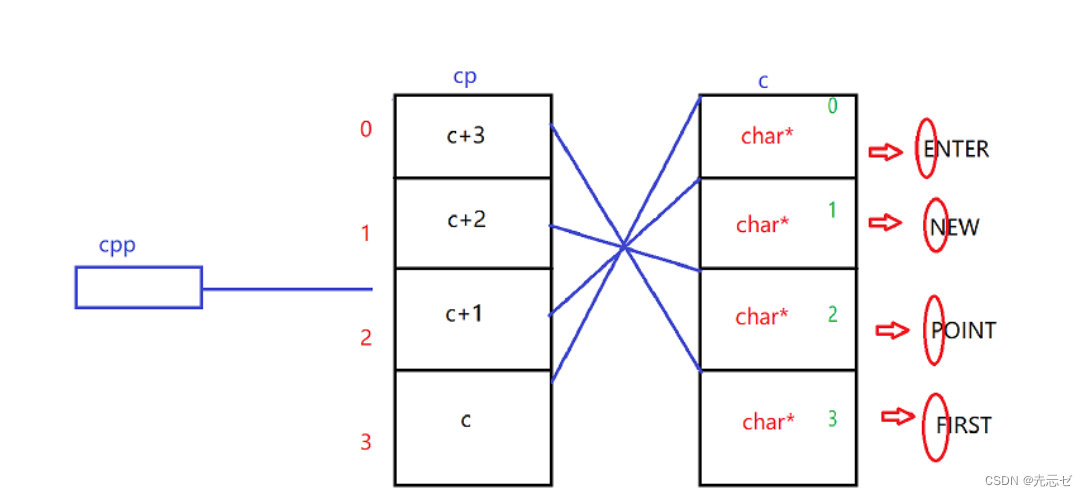
【数组及指针经典笔试题解析】
1.数组和指针笔试题 题目1 int main(){int a[5] { 1,2,3,4,5};int * ptr (int * )(&a 1);printf("%d,%d",*(a 1),*(ptr - 1));return 0;}图文解析: int * ptr …...
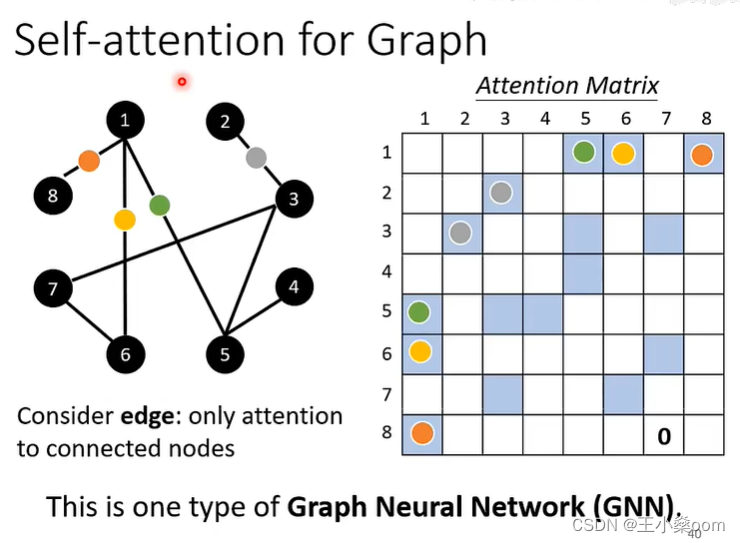
Transformer学习-self-attention
这里写自定义目录标题 Self-attentionMulti-head self-attention用self-attention解决其他问题 Self-attention 用Wq、Wk、Wv分别乘输入向量得到q、k、v向量 用每个q向量乘所有的k向量得到对应项的attention,即用每项的query向量去匹配所有的key向量,得…...

Spring Boot:利用JPA进行数据库的增改
目录 JPA介绍Service接口Service和Autowired示例代码 Dao数据库操作层Repository示例代码 控制器文件示例代码-增加增加成功示例代码-修改修改成功 JPA介绍 JPA(Javaa Persistence API)一种用于持久化 Java 对象到关系型数据库的标准规范。它提供了一种统一的方式来…...
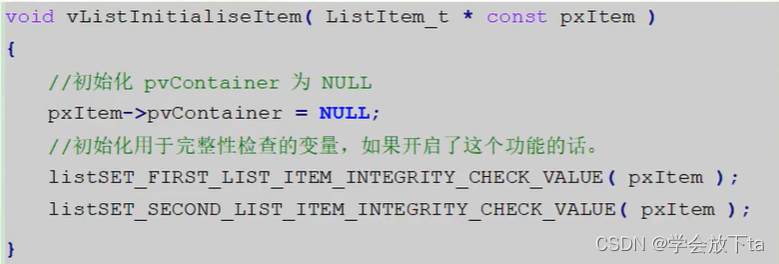
列表的增删改查和遍历
任务概念 什么是任务 任务是一个参数为指针,无法返回的函数,函数体为死循环不能返回任务的实现过程 每个任务是独立的,需要为任务分别分配栈称为任务栈,通常是预定义的全局数组,也可以是动态分配的一段内存空间&#…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...
C++中vector类型的介绍和使用
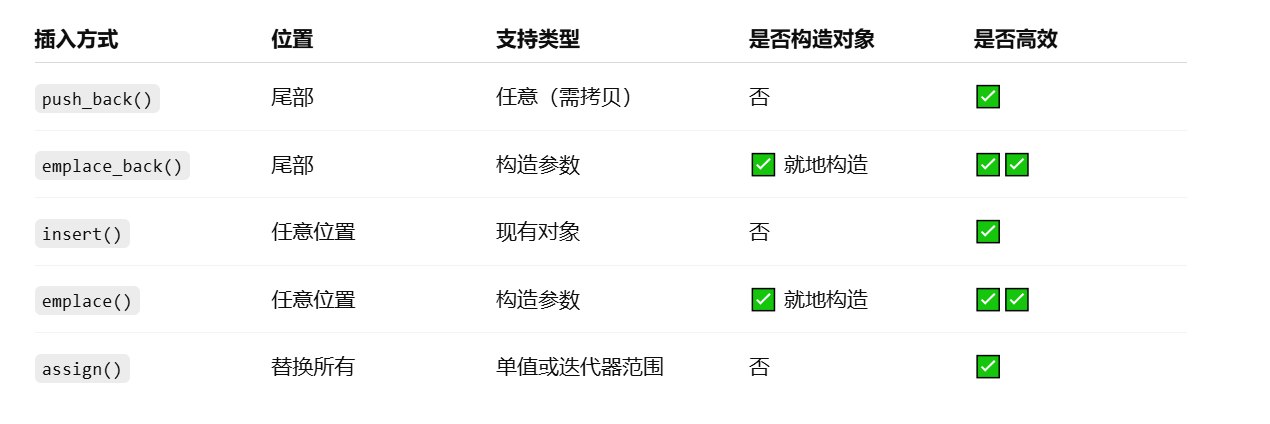
文章目录 一、vector 类型的简介1.1 基本介绍1.2 常见用法示例1.3 常见成员函数简表 二、vector 数据的插入2.1 push_back() —— 在尾部插入一个元素2.2 emplace_back() —— 在尾部“就地”构造对象2.3 insert() —— 在任意位置插入一个或多个元素2.4 emplace() —— 在任意…...

[QMT量化交易小白入门]-六十二、ETF轮动中简单的评分算法如何获取历史年化收益32.7%
本专栏主要是介绍QMT的基础用法,常见函数,写策略的方法,也会分享一些量化交易的思路,大概会写100篇左右。 QMT的相关资料较少,在使用过程中不断的摸索,遇到了一些问题,记录下来和大家一起沟通,共同进步。 文章目录 相关阅读1. 策略概述2. 趋势评分模块3 代码解析4 木头…...

WinUI3开发_使用mica效果
简介 Mica(云母)是Windows10/11上的一种现代化效果,是Windows10/11上所使用的Fluent Design(设计语言)里的一个效果,Windows10/11上所使用的Fluent Design皆旨在于打造一个人类、通用和真正感觉与 Windows 一样的设计。 WinUI3就是Windows10/11上的一个…...
