【强化学习】05 —— 基于无模型的强化学习(Prediction)
文章目录
- 简介
- 蒙特卡洛算法
- 时序差分方法
- Example1
- MC和TD的对比
- 偏差(Bias)/方差(Variance)的权衡
- Example2 Random Walk
- Example3 AB
- 反向传播(backup)
- Monte-Carlo Backup
- Temporal-Difference Backup
- Dynamic Programming Backup
- Bootstrapping and Sampling
- 多步时序查分学习
- Example4 Large Random Walk Example
- Forward-view TD(λ)
- Backward View TD(λ)
- Eligibility Traces
- 总结
- 参考
Model-free prediction
Estimate the value function of an unknown MDP
简介
上一节讲到的动态规划算法(【强化学习】04 ——动态规划算法
)要求马尔可夫决策过程是已知的,即要求与智能体交互的环境是完全已知的(例如迷宫或者给定规则的网格世界)。在此条件下,智能体其实并不需要和环境真正交互来采样数据,直接用动态规划算法就可以解出最优价值或策略。
这类已经给定一个MDP模型(即,状态转移 P s s ′ a \mathcal P_{ss'}^a Pss′a和奖励函数 R s \mathcal R_s Rs明确给定) 的算法可以称为基于模型的强化学习。基于模型来计算最优价值函数和学习最优的策略。
但这在大部分场景下并不现实,机器学习的主要方法都是在数据分布未知的情况下针对具体的数据点来对模型做出更新的。对于大部分强化学习现实场景(例如电子游戏或者一些复杂物理环境),其马尔可夫决策过程的状态转移概率是无法写出来的,也就无法直接进行动态规划。在这种情况下,智能体只能和环境进行交互,通过采样到的数据来学习,这类学习方法统称为无模型的强化学习(model-free reinforcement learning)。
蒙特卡洛算法
蒙特卡洛算法(Monte-Carlo method)和时序差分算法(temporal difference,TD)就是典型的无模型的强化学习。在【强化学习】03 ——马尔可夫决策过程中已经对MC有过介绍。这里再做几点补充与总结。
思路: V ( S t ) ≃ 1 N ∑ i = 1 N G t ( i ) 增量式实现: V ( S t ) ← V ( S t ) + α ( G t − V ( S t ) ) \begin{aligned}&\text{思路:}\quad&V(S_t)\simeq\frac1N\sum_{i=1}^NG_t^{(i)}\\&\text{增量式实现:}\quad&V(S_t)\leftarrow V(S_t)+\alpha\big(G_t-V(S_t)\big)\end{aligned} 思路:增量式实现:V(St)≃N1i=1∑NGt(i)V(St)←V(St)+α(Gt−V(St))
-
蒙特卡洛方法:直接从经验片段进行学习
-
蒙特卡洛是模型无关的:未知马尔可夫决策过程的状态转移/奖励
-
蒙特卡洛从完整的片段中进行学习:没有使用bootstrapping的方法
-
蒙特卡洛采用最简单的思想:值(value)= 平均累计奖励(mean return)
-
注意:只能将蒙特卡洛方法应用于有限长度的马尔可夫决策过程中
- 即,所有的片段都有终止状态
-
蒙特卡洛策略评估使用经验均值累计奖励而不是期望累计奖励
- 值函数(value function)是期望累计奖励
-
first-visit MC
- 对于一个episode,只计算一次状态 s s s的回报,之后再出现状态 s s s,则不去计算。
- 参考伪代码

-
every-visit MC
- 在状态 s s s每一次出现时计算它的回报
时序差分方法
时序差分是一种用来估计一个策略的价值函数的方法,它结合了蒙特卡洛和动态规划算法的思想。时序差分方法和蒙特卡洛的相似之处在于可以从样本数据中学习,不需要事先知道环境;和动态规划的相似之处在于根据贝尔曼方程的思想,利用后续状态的价值估计来更新当前状态的价值估计。回顾一下蒙特卡洛方法对价值函数的增量更新方式: V ( s t ) ← V ( s t ) + α [ G t − V ( s t ) ] V(s_t)\leftarrow V(s_t)+\alpha[G_t-V(s_t)] V(st)←V(st)+α[Gt−V(st)]
其中 α \alpha α为对价值估计更新的步长,可以是个常量,因此也可以将上述方式称为constant- α \alpha α MC。蒙特卡洛方法必须要等整个序列结束之后才能计算得到这一次的回报 G t G_t Gt,而时序差分方法只需要当前步结束即可进行计算。具体来说,时序差分算法用当前获得的奖励 R t + 1 R_{t+1} Rt+1加上下一个状态的价值估计 V ( S t + 1 ) V(S_{t+1}) V(St+1)来作为在当前状态会获得的回报,即: V ( S t ) ← V ( S t ) + α [ R t + 1 + γ V ( S t + 1 ) − V ( S t ) ] \begin{aligned}V(S_t)\leftarrow V(S_t)+\alpha\Big[R_{t+1}+\gamma V(S_{t+1})-V(S_t)\Big]\end{aligned} V(St)←V(St)+α[Rt+1+γV(St+1)−V(St)]上述这种TD方法称为 T D ( 0 ) TD(0) TD(0),或者说是一步TD算法,之后还会介绍 T D ( λ ) TD(\lambda) TD(λ)算法,或者称为n-step 的TD算法。 R t + 1 + γ V ( S t + 1 ) R_{t+1}+\gamma V(S_{t+1}) Rt+1+γV(St+1)被称为时序差分目标(TD Target) R t + 1 + γ V ( S t + 1 ) − V ( S t ) R_{t+1}+\gamma V(S_{t+1})-V(S_t) Rt+1+γV(St+1)−V(St)被称为时序差分误差( TD error),时序差分算法将时序差分误差与步长的乘积作为状态价值的更新量。。下面是TD(0)的算法伪代码:
可以用 R t + 1 + γ V ( S t + 1 ) R_{t+1}+\gamma V(S_{t+1}) Rt+1+γV(St+1)代替 G t G_t Gt的原因是: V π ( s ) = E π [ G t ∣ S t = s ] = E π [ ∑ k = 0 ∞ γ k R t + k + 1 ∣ S t = s ] = E π [ R t + 1 + γ ∑ k = 0 ∞ γ k R t + k + 2 ∣ S t = s ] = E π [ R t + 1 + γ V π ( S t + 1 ) ∣ S t = s ] \begin{aligned} V_{\pi}(s)& =\mathbb{E}_\pi[G_t|S_t=s] \\ &=\mathbb{E}_\pi[\sum_{k=0}^\infty\gamma^kR_{t+k+1}|S_t=s] \\ &=\mathbb{E}_\pi[R_{t+1}+\gamma\sum_{k=0}^\infty\gamma^kR_{t+k+2}|S_t=s] \\ &=\mathbb{E}_\pi[R_{t+1}+\gamma V_\pi(S_{t+1})|S_t=s] \end{aligned} Vπ(s)=Eπ[Gt∣St=s]=Eπ[k=0∑∞γkRt+k+1∣St=s]=Eπ[Rt+1+γk=0∑∞γkRt+k+2∣St=s]=Eπ[Rt+1+γVπ(St+1)∣St=s]因此蒙特卡洛方法将上式第一行作为更新的目标,而时序差分算法将上式最后一行作为更新的目标。于是,在用策略和环境交互时,每采样一步,我们就可以用时序差分算法来更新状态价值估计。
Example1
每天下班开车回家时,你都试图预测回家需要多长时间。当你离开办公室时,你会注意时间、一周中的哪一天、天气以及其他任何可能相关的事情。假设这个星期五你正好在6点离开,你估计需要30分钟才能到家。当你到达你的车时,已经是6:05了,你注意到天开始下雨了。雨天交通通常较慢,所以你重新估计从那时起需要35分钟,总共需要40分钟。15分钟后,你顺利地完成了高速公路部分的旅程。当你从一条二级公路上下来时,你把总的旅行时间估计减少到35分钟。不幸的是,在这一点上,你被一辆慢车挡住了,而这条路太窄,无法超车。你最终不得不跟着卡车,直到你在6:40转弯到你住的街道。三分钟后你就到家了。因此,状态、时间和预测的序列如下:
下图是MC和TD算法基于上述问题的对比。可以看到蒙特卡洛是等待片段结束,估计总的时间;而TD则是依据下一步进行估计。

MC和TD的对比
时序差分:能够在知道最后结果之前进行学习
• 时序差分能够在每一步之后进行在线学习
• 蒙特卡洛必须等待片段结束,直到累计奖励已知
时序差分:能够无需最后结果地进行学习
• 时序差分能够从不完整的序列中学习
• 蒙特卡洛只能从完整序列中学习
• 时序差分在连续(无终止的)环境下工作
• 蒙特卡洛只能在片段化的(有终止的)环境下工作
偏差(Bias)/方差(Variance)的权衡
-
累计奖励 G t = R t + 1 + γ R t + 2 + ⋯ + γ T − 1 R T \begin{aligned}G_t=R_{t+1}+\gamma R_{t+2}+\cdots+\gamma^{T-1}R_T\end{aligned} Gt=Rt+1+γRt+2+⋯+γT−1RT是 V π ( S t ) V_\pi(S_t) Vπ(St)的无偏估计
-
时序差分真实目标 R t + 1 + γ V π ( S t + 1 ) R_{t+1}+\gamma V_\pi(S_{t+1}) Rt+1+γVπ(St+1)是对 V π ( S t ) V_\pi(S_t) Vπ(St)的无偏估计
-
时序差分目标 R t + 1 + γ V ( S t + 1 ) R_{t+1}+\gamma V(S_{t+1}) Rt+1+γV(St+1)是对 V π ( S t ) V_\pi(S_t) Vπ(St)的有偏估计
-
时序差分目标具有比累计奖励更低的方差
• 累计奖励——取决于多步随机动作,多步状态转移和多步奖励,多步随机可能带来更多的不确定性。
• 时序差分目标——取决于单步随机动作,单步状态转移和单步奖励
| MC: V ( s t ) ← V ( s t ) + α [ G t − V ( s t ) ] V(s_t)\leftarrow V(s_t)+\alpha[G_t-V(s_t)] V(st)←V(st)+α[Gt−V(st)] | TD: V ( S t ) ← V ( S t ) + α [ R t + 1 + γ V ( S t + 1 ) − V ( S t ) ] \begin{aligned}V(S_t)\leftarrow V(S_t)+\alpha\Big[R_{t+1}+\gamma V(S_{t+1})-V(S_t)\Big]\end{aligned} V(St)←V(St)+α[Rt+1+γV(St+1)−V(St)] |
|---|---|
| 蒙特卡洛具有高方差,无偏差 | 时序差分具有低方差,有偏差 |
| • 良好的收敛性质 | • 通常比蒙特卡洛更加高效 |
| • 使用函数近似时依然如此 | • 时序差分最终收敛到 V π ( S t ) V_\pi(S_t) Vπ(St) |
| • 对初始值不敏感 | • 但使用函数近似并不总是如此 |
| • 易于理解和使用 | • 比蒙特卡洛对初始值更加敏 |
Example2 Random Walk
在这个例子中,我们将TD(0)和constant-αMC应用于以下马尔可夫奖励过程,对它们的预测能力进行了比较:

在这个MRP中,所有的情节都以中心状态C开始,然后每个步骤都向左或向右移动一个状态,概率相等。情节要么在最左边终止,要么在最右边终止。当情节在右侧终止时,发生+1的奖励;所有其他奖励都是零。例如,一个典型的情节可能包括以下状态和奖励序列:C,0,B,0,C,0,D,0,E,1。由于此任务是未打折的,因此每个状态的真实值是从该状态开始终止于右侧的概率。因此,中心状态的真实值为 V π ( C ) V_\pi(C) Vπ(C)=0.5。状态A到E的真实值是1/6、2/6、3/6、4/6和5/6。

可以看到随着采样次数的增多,或越来越接近真实值。

从图中可以看出,MC比TD的收敛速度要慢上许多,同时MC的均方根误差要比TD大上不少。
Example3 AB
从上面的例子中我们知道,当 E p i s o d e s → ∞ Episodes\to\infty Episodes→∞时,MC和TD都可以使得 V ( s ) V(s) V(s)收敛到 V π ( s ) V_\pi(s) Vπ(s)。接下来,我们将会讨论有限个Episodes的问题:用有限个Episodes反复训练MC和TD。
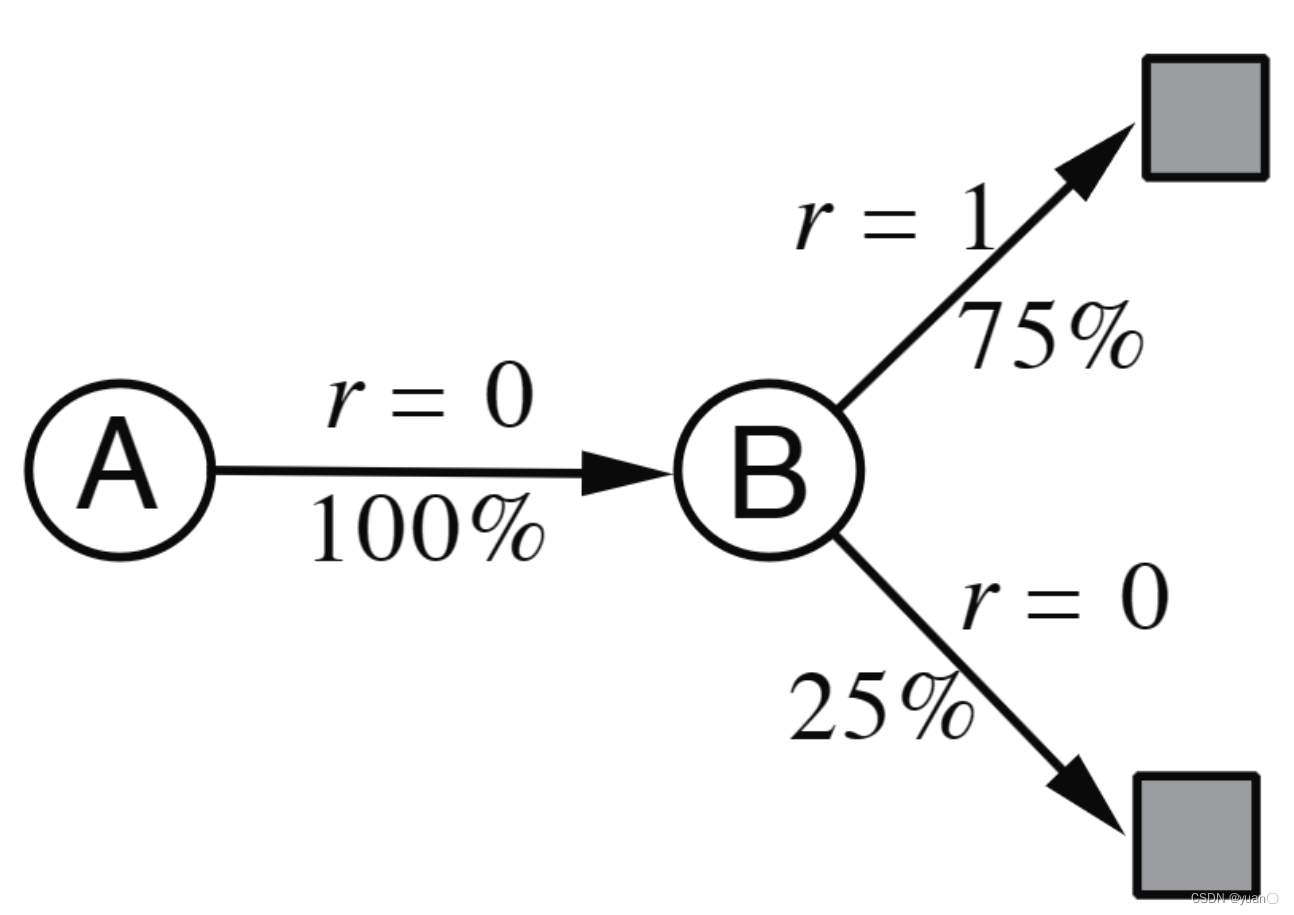
以下面的双状态AB例子为例,一共8个Episode。依据这些数据,求解出 V ( A ) , V ( B ) V(A),V(B) V(A),V(B)

很容易知道 V ( B ) = 0.75 V(B)=0.75 V(B)=0.75,但对于 V ( A ) V(A) V(A)的求解,MC和TD会给出两种不同的答案。
- MC收敛于具有最小均方根误差的解
- 会对已有的经验求取最小均方根误差
- ∑ k = 1 K ∑ t = 1 T k ( G t k − V ( s t k ) ) 2 \begin{aligned}\sum_{k=1}^K\sum_{t=1}^{T_k}\left(G_t^k-V(s_t^k)\right)^2\end{aligned} k=1∑Kt=1∑Tk(Gtk−V(stk))2
- 因此,对于MC, V ( A ) = 0 V(A)=0 V(A)=0
- TD(0)收敛于极大似然马尔可夫模型的解
- 基于MDP ⟨ S , A , P ^ , R ^ , γ ⟩ \langle S,A,\hat P,\hat R,\gamma \rangle ⟨S,A,P^,R^,γ⟩去拟合数据
- P ^ s , s ′ a = 1 N ( s , a ) ∑ k = 1 k ∑ t = 1 T k 1 ( s t k , a t k , s t + 1 k = s , a , s ′ ) R ^ s a = 1 N ( s , a ) ∑ k = 1 k ∑ t = 1 T k 1 ( s t k , a t k = s , a ) r t k \begin{aligned}\hat{\mathcal{P}}_{s,s^{\prime}}^a&=\frac1{N(s,a)}\sum_{k=1}^k\sum_{t=1}^{T_k}\mathbf{1}(s_t^k,a_t^k,s_{t+1}^k=s,a,s^{\prime})\\\hat{\mathcal{R}}_s^a&=\frac1{N(s,a)}\sum_{k=1}^k\sum_{t=1}^{T_k}\mathbf{1}(s_t^k,a_t^k=s,a)r_t^k\end{aligned} P^s,s′aR^sa=N(s,a)1k=1∑kt=1∑Tk1(stk,atk,st+1k=s,a,s′)=N(s,a)1k=1∑kt=1∑Tk1(stk,atk=s,a)rtk
- 因此,对于TD, V ( A ) = 0.75 V(A)=0.75 V(A)=0.75
- TD利用Markov特性
- 通常在马尔可夫环境中更有效
- MC不利用Markov属性
- 通常在非马尔可夫环境中更有效
反向传播(backup)
Monte-Carlo Backup
MC的反向传播需要通过不断地采样,最终抵达终点时,结束采样并计算 G t G_t Gt

Temporal-Difference Backup
而TD只需进行一步

Dynamic Programming Backup
动态规划同样是一步,但是是对下一步的所有可能的状态作估计。

下图是DP、枚举法、MC以及TD四种算法的比较。

Bootstrapping and Sampling
| Bootstrapping:update involves an estimate | Sampling:update samples an expectation |
|---|---|
| MC does not bootstrap | MC samples |
| DP bootstraps | DP does not sample |
| TD bootstraps | TD samples |
多步时序查分学习
除了往前探一步,我们还可以往前探 n n n步。

定义𝑛步累计奖励:
G t ( n ) = R t + 1 + γ R t + 2 + . . . + γ n − 1 R t + n + γ n V ( S t + n ) G_t^{(n)}=R_{t+1}+\gamma R_{t+2}+...+\gamma^{n-1}R_{t+n}+\gamma^nV(S_{t+n}) Gt(n)=Rt+1+γRt+2+...+γn−1Rt+n+γnV(St+n)
因此,𝑛步时序差分学习为:
V ( S t ) ← V ( S t ) + α ( G t ( n ) − V ( S t ) ) V(S_t)\leftarrow V(S_t)+\alpha\left(G_t^{(n)}-V(S_t)\right) V(St)←V(St)+α(Gt(n)−V(St))
伪代码如下:

Example4 Large Random Walk Example
对于多步时序查分,可以从下图中看到,当 n → ∞ n\to\infty n→∞时,平均均方根误差越大,符合MC方差大的特性。同时,不同的 n n n所产生的效果也不同,最佳点(平均均方根误差最小的点处,即极小值点处)的选择也不尽相同,对于一个问题,可能 n = 4 n=4 n=4时比较好,但对于另一个问题,则是 n = 2 n=2 n=2比较好。因此我们需要考虑一种能够兼顾所有 n n n的算法,以增强鲁棒性。

Forward-view TD(λ)
举个例子:

我们可以对 n = 2 n=2 n=2和 n = 4 n=4 n=4的累计奖励进行平均: 1 2 G ( 2 ) + 1 2 G ( 4 ) \frac12G^{(2)}+\frac12G^{(4)} 21G(2)+21G(4),以此来进行平衡。同样地,我们可以扩展到所有的步长:
这个算法被称为λ-return算法。该算法组合了所有的 G t ( n ) G_t^{(n)} Gt(n),并且赋上了相应的权值 ( 1 − λ ) λ n − 1 (1-\lambda)\lambda^{n-1} (1−λ)λn−1,累计奖励为: G t λ = ( 1 − λ ) ∑ n = 1 ∞ λ n − 1 G t ( n ) G_t^\lambda=(1-\lambda)\sum_{n=1}^\infty\lambda^{n-1}G_t^{(n)} Gtλ=(1−λ)n=1∑∞λn−1Gt(n)
因此,TD(λ)为 V ( S t ) ← V ( S t ) + α ( G t λ − V ( S t ) ) V(S_t)\leftarrow V(S_t)+\alpha\left(G_t^\lambda-V(S_t)\right) V(St)←V(St)+α(Gtλ−V(St))

以上讲述的算法为Forward-view TD(λ):
- 基于λ-return更新价值函数
- Forward-view looks into the future to compute G t λ G_t^{\lambda} Gtλ
- 不过对于这种算法(Forward-view TD(λ)),也是和MC一样需要从完整的片段中进行学习。
Backward View TD(λ)
此部分不完整
Backward View TD(λ)是另一种算法,无需从完整的片段中进行学习。
- Forward view provides theory
- Backward view provides mechanism
- Update online, every step, from incomplete sequences
Eligibility Traces

例子:如图所示,响三声铃铛再亮了一个灯泡,之后发生触电,那么是什么行为导致触电的呢?bell or light?
基于此,有两种启发式算法:
- Frequency heuristic: 按频率进行启发
- Recency heuristic: 按离得最近的进行启发
- 而Eligibility Traces则综合了以上两种启发方式: E 0 ( s ) = 0 E t ( s ) = γ λ E t − 1 ( s ) + 1 ( S t = s ) \begin{aligned}&E_0(s)=0\\&E_t(s)=\gamma\lambda E_{t-1}(s)+\mathbf{1}(S_t=s)\end{aligned} E0(s)=0Et(s)=γλEt−1(s)+1(St=s)当访问一个节点时,会使得Eligibility Trace增加,而不访问时,则会随时间衰退。

基于Eligibility Traces,我们可以得到Backward View TD(λ):
- Keep an eligibility trace for every state s
- Update value V ( s ) V(s) V(s)for every state s
- In proportion to TD-error δ t δ_t δt and eligibility trace E t ( s ) E_t(s) Et(s)。(下面这个TD-error是1-step的)
δ t = R t + 1 + γ V ( S t + 1 ) − V ( S t ) V ( s ) ← V ( s ) + α δ t E t ( s ) \begin{aligned}\delta_t&=R_{t+1}+\gamma V(S_{t+1})-V(S_t)\\V(s)&\leftarrow V(s)+\alpha\delta_tE_t(s)\end{aligned} δtV(s)=Rt+1+γV(St+1)−V(St)←V(s)+αδtEt(s)

当 λ = 0 λ = 0 λ=0时,只有当前状态被更新 E t ( s ) = 1 ( S t = s ) V ( s ) ← V ( s ) + α δ t E t ( s ) \begin{aligned}&E_t(s)=\mathbf{1}(S_t=s)\\&V(s)\leftarrow V(s)+\alpha\delta_tE_t(s)\end{aligned} Et(s)=1(St=s)V(s)←V(s)+αδtEt(s)也就等效于TD(0)
当 λ = 1 λ = 1 λ=1时,需要用到整个episode,同时可以进行离线更新。对于其中一个episode,TD(1) 的累计更新方式与MC基本相同。
对于一个episode,从时间 k k k处的 s s s开始,
- TD(1) eligibility trace会随着时间打折扣 E t ( s ) = γ E t − 1 ( s ) + 1 ( S t = s ) = { 0 i f t < k γ t − k i f t ≥ k \begin{gathered} E_t(s) =\gamma E_{t-1}(s)+1(S_t=s) \\ \left.=\left\{\begin{array}{ll}0&\mathrm{~if~}t<k\\\gamma^{t-k}&\mathrm{~if~}t\geq k\end{array}\right.\right. \end{gathered} Et(s)=γEt−1(s)+1(St=s)={0γt−k if t<k if t≥k
- TD(1)在线更新累计误差 ∑ t = 1 T − 1 α δ t E t ( s ) = α ∑ t = k T − 1 γ t − k δ t = α ( G k − V ( S k ) ) \sum_{t=1}^{T-1}\alpha\delta_tE_t(s)=\alpha\sum_{t=k}^{T-1}\gamma^{t-k}\delta_t=\color{red}\alpha\left(G_k-V(S_k)\right) t=1∑T−1αδtEt(s)=αt=k∑T−1γt−kδt=α(Gk−V(Sk))
- 在episode的最后,累计所有的error δ k + γ δ k + 1 + γ 2 δ k + 2 + . . . + γ T − 1 − k δ T − 1 \delta_k+\gamma\delta_{k+1}+\gamma^2\delta_{k+2}+...+\gamma^{T-1-k}\delta_{T-1} δk+γδk+1+γ2δk+2+...+γT−1−kδT−1 δ t + γ δ t + 1 + γ 2 δ t + 2 + . . . + γ T − 1 − t δ T − 1 = R t + 1 + γ V ( S t + 1 ) − V ( S t ) + γ R t + 2 + γ 2 V ( S t + 2 ) − γ V ( S t + 1 ) + γ 2 R t + 3 + γ 3 V ( S t + 3 ) − γ 2 V ( S t + 2 ) + γ T − 1 − t R T + γ T − t V ( S T ) − γ T − 1 − t V ( S T − 1 ) … = R t + 1 + γ R t + 2 + γ 2 R t + 3 . . . + γ T − 1 − t R T − V ( S t ) = G t − V ( S t ) \begin{aligned} &\delta_t+\gamma\delta_{t+1}+\gamma^2\delta_{t+2}+...+\gamma^{T-1-t}\delta_{T-1} \\ &=R_{t+1}+\gamma V(S_{t+1})-V(S_t) \\ &+\gamma R_{t+2}+\gamma^2V(S_{t+2})-\gamma V(S_{t+1}) \\ &+\gamma^2R_{t+3}+\gamma^3V(S_{t+3})-\gamma^2V(S_{t+2}) \\ &+\gamma^{T-1-t}R_T+\gamma^{T-t}V(S_T)-\gamma^{T-1-t}V(S_{T-1}) \\&\dots\\ &=R_{t+1}+\gamma R_{t+2}+\gamma^2R_{t+3}...+\gamma^{T-1-t}R_T-V(S_t) \\ &=\color{red}G_t-V(S_t) \end{aligned} δt+γδt+1+γ2δt+2+...+γT−1−tδT−1=Rt+1+γV(St+1)−V(St)+γRt+2+γ2V(St+2)−γV(St+1)+γ2Rt+3+γ3V(St+3)−γ2V(St+2)+γT−1−tRT+γT−tV(ST)−γT−1−tV(ST−1)…=Rt+1+γRt+2+γ2Rt+3...+γT−1−tRT−V(St)=Gt−V(St)
- TD(1)大致相当于every-visit Monte-Carlo
- error是在线累积的,循序渐进
- 如果价值函数仅在episode结束时离线更新
- 那么总更新与MC完全相同
总结

参考
[1] 伯禹AI
[2] https://www.deepmind.com/learning-resources/introduction-to-reinforcement-learning-with-david-silver
[3] 动手学强化学习
[4] Reinforcement Learning
相关文章:

【强化学习】05 —— 基于无模型的强化学习(Prediction)
文章目录 简介蒙特卡洛算法时序差分方法Example1 MC和TD的对比偏差(Bias)/方差(Variance)的权衡Example2 Random WalkExample3 AB 反向传播(backup)Monte-Carlo BackupTemporal-Difference BackupDynamic Programming Backup Boot…...
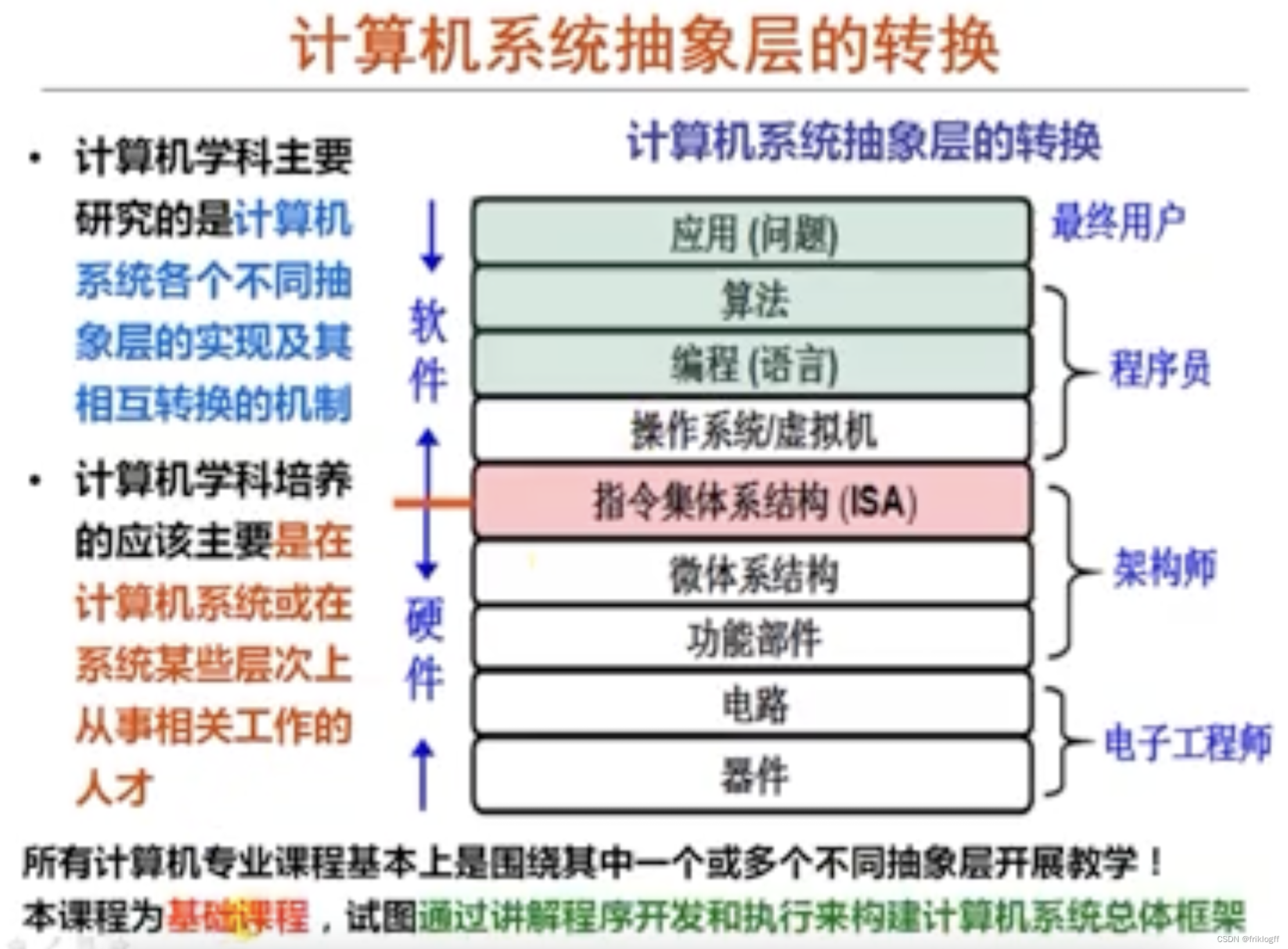
【计算机组成原理】考研真题攻克与重点知识点剖析 - 第 1 篇:计算机系统概述
前言 本文基础知识部分来自于b站:分享笔记的好人儿的思维导图,感谢大佬的开源精神,习题来自老师划的重点以及考研真题。此前我尝试了完全使用Python或是结合大语言模型对考研真题进行数据清洗与可视化分析,本人技术有限ÿ…...

【Java-LangChain:面向开发者的提示工程-8】聊天机器人
第八章 聊天机器人 使用一个大型语言模型的一个令人兴奋的事情是,我们可以用它来构建一个定制的聊天机器人 (Chatbot) ,只需要很少的工作量。在这一节中,我们将探索如何利用聊天的方式,与个性化(或专门针对特定任务或…...

利用t.ppft.interval分别计算T分布置信区间[实例]
scipy.stats.t.interval用于计算t分布的置信区间,即给定置信水平时,计算对应的置信区间的下限和上限。 scipy.stats.t.ppf用于计算t分布的百分位点,即给定百分位数(概率)时,该函数返回给定百分位数对应的t…...
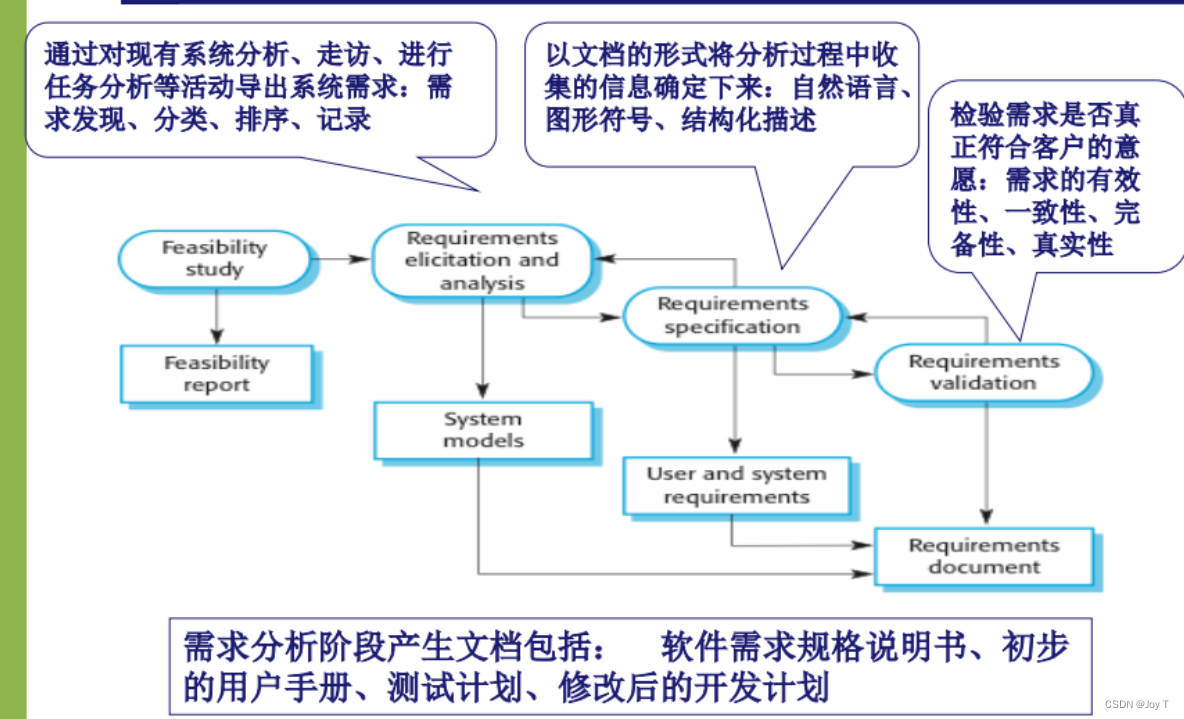
软件工程第三周
可行性研究 续 表达工作量的方式 LOC估算:Line of Code 估算公式S(Sopt4SmSpess)/6 FP:功能点 1. LOC (Line of Code) 估算 定义:LOC是指一个软件项目中的代码行数。 2. FP (Function Points) 估算 定义:FP是基于软件的功能性和…...
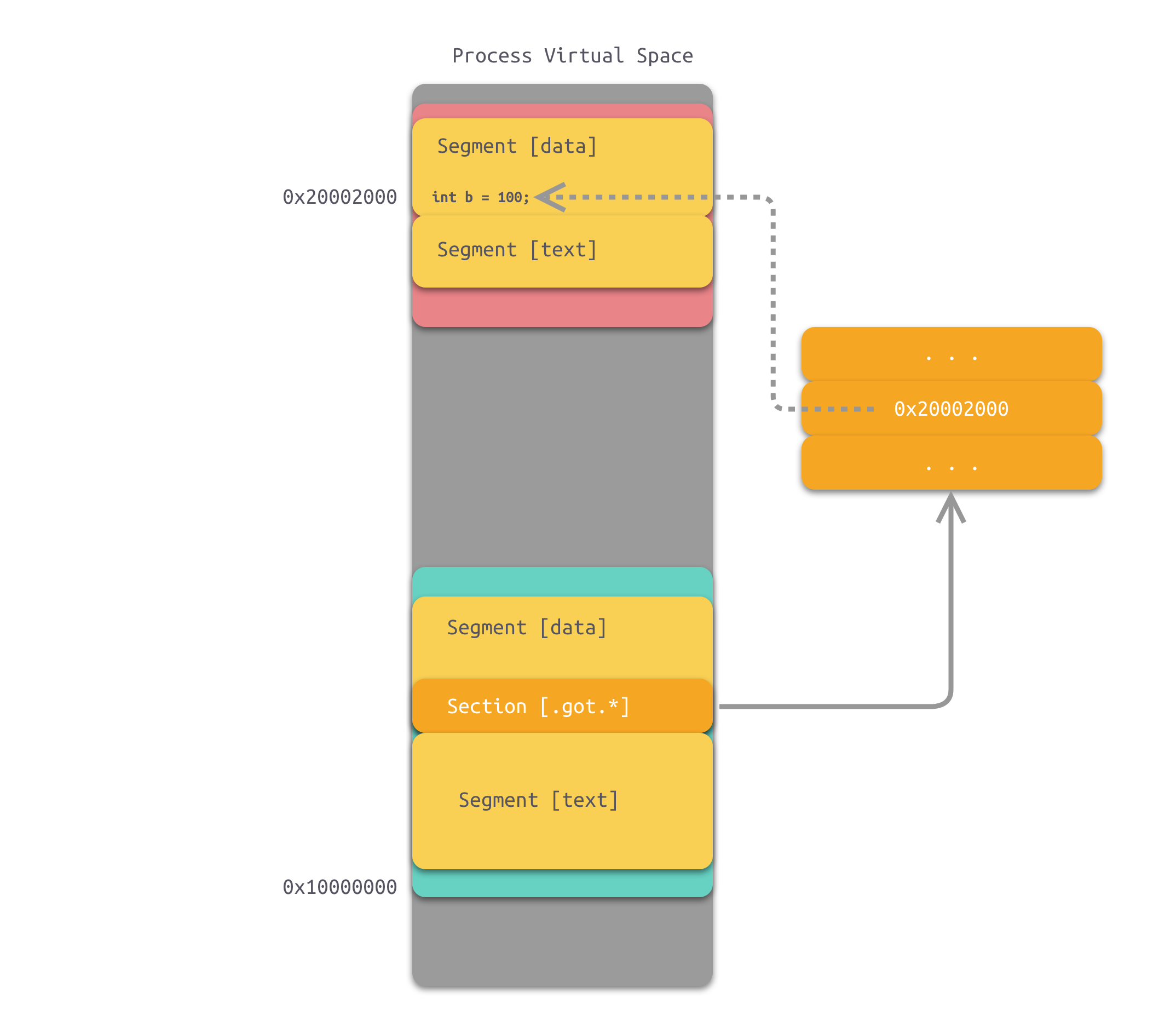
动态链接那些事
1、为什么要动态链接 1.1 空间浪费 对于静态链接来说,在程序运行之前,会将程序所需的所有模块编译、链接成一个可执行文件。这种情况下,如果 Program1 和 Program2 都需要用到 Lib.o 模块,那么,内存中和磁盘中实际上就…...

力扣:118. 杨辉三角(Python3)
题目: 给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。 在「杨辉三角」中,每个数是它左上方和右上方的数的和。 来源:力扣(LeetCode) 链接:力扣(LeetCode)官…...

QGIS文章二——DEM高程裁剪和3D地形图
经常看到别人基于高程文件制作出精美的3D地图,笔者按照互联网几种制作方式进行尝试后,写的DEM高程裁剪和3D地形图教程,或许其中有一些错误的,也请指出。 本文基于海南省的shp文件和海南省DEM高程文件,制作海口地区的3D…...

【kubernetes】kubernetes中的StatefulSet使用
TOC 1 为什么需要StatefulSet 常规的应用通常使用Deployment,如果需要在所有机器上部署则使用DaemonSet,但是有这样一类应用,它们在运行时需要存储一些数据,并且当Pod在其它节点上重建时也希望这些数据能够在重建后的Pod上获取&…...

创建文件夹
/storage/emulated/0/代码文件/ 没有就创建 文件名命名方法:编号. 库 时间戳 使用Python的os模块来检查目录是否存在,并在不存在时创建它。下面是一个示例代码,演示了如何检查指定路径下的目录是否存在,若不存在则创建…...

点击router-link时候会发生什么?
当你点击链接或按钮时,将会导航到 User 组件,就会显示相应的用户 ID。 这里说一下执行流程,当点击一个 router-link 时,Vue Router会执行以下流程: 1)点击事件触发: 当你点击 router-link 组件时…...

【Spring】@Bean方法中存在继承如何分析
文章目录 1. 提问:如果让您分析Spring MVC的原理,您如何开始分析呢2. 如何破局3. 资料参考 本文主要介绍:如何分析 Bean方法存在继承 或 Bean方法中存在调用子类方法。 1. 提问:如果让您分析Spring MVC的原理,您如何…...

【Vim 插件管理器】Vim-plug和Vim-vbundle的区别
- vundle是一款老款的插件管理工具 - vim-plug相对较新,特点是支持异步加载,相比vundle而言 Vim-plug 是一个自由、开源、速度非常快的、极简的 vim 插件管理器。它可以并行地安装或更新插件。你还可以回滚更新。它创建浅层克隆shallow clone最小化磁盘…...

电子计算机核心发展(继电器-真空管-晶体管)
目录 继电器 最大的机电计算机之一——哈弗Mark1号,IBM1944年 背景 组成 性能 核心——继电器 简介 缺点 速度 齿轮磨损 Bug的由来 真空管诞生 组成 控制开关电流 继电器对比 磨损 速度 缺点 影响 代表 第一个可编程计算机 第一个真正通用&am…...
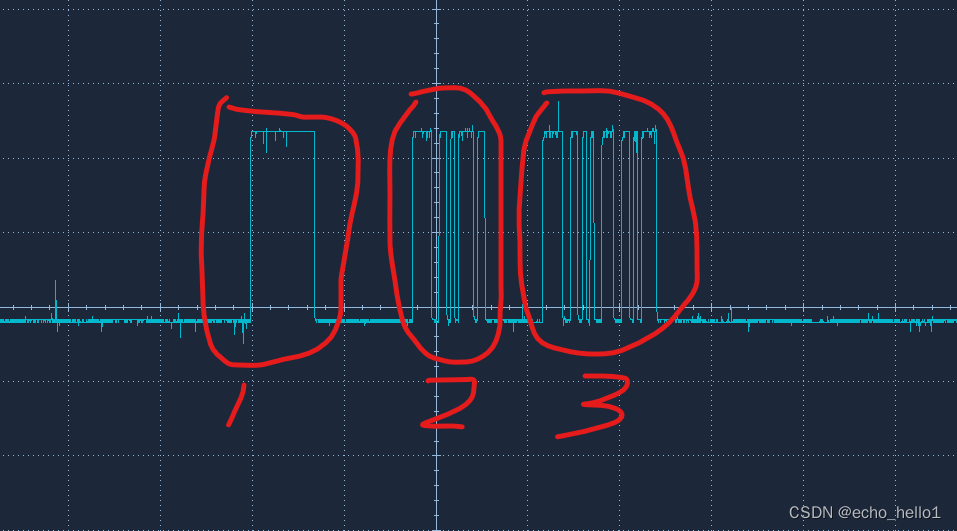
SDI-12协议与STM32 进行uart通信
场景是用stm32与一款温湿度传感器通信,不过是基于SDI-12协议,SDI-12时序和UART类似,故采用UART传输,原理图如下 其中DIR_OUT_SDI是一个IO引脚,控制UART_TX_SDI是否使能,U10是三态门IC,即拉低DIR…...

JS中的强制类型转换
JavaScript 中有多种强制类型转换的方式,可以将一个数据类型转换为另一种数据类型。这可以通过一些内置函数或操作符来实现。 显式类型转换(强制类型转换): 显式类型转换是通过特定的函数或操作符来明确指定要进行的类型转换。以下…...
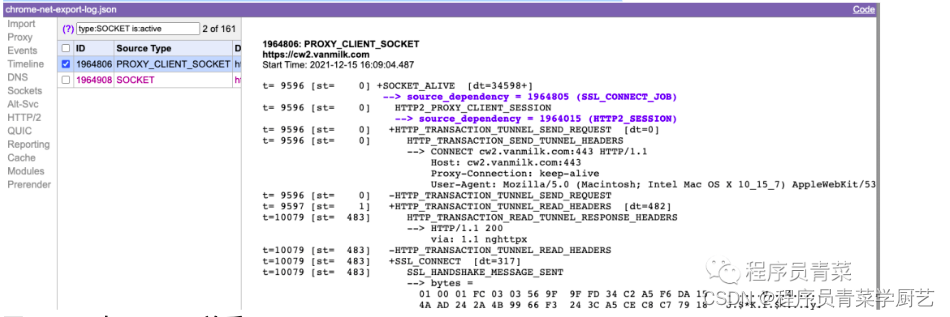
WebSocket实战之四WSS配置
一、前言 上一篇文章WebSocket实战之三遇上PAC ,碰到的问题只能上安全的WebSocket(WSS)才能解决,配置证书还是挺麻烦的,主要是每年都需要重新更新证书,我配置过的证书最长有效期也只有两年,搞不…...
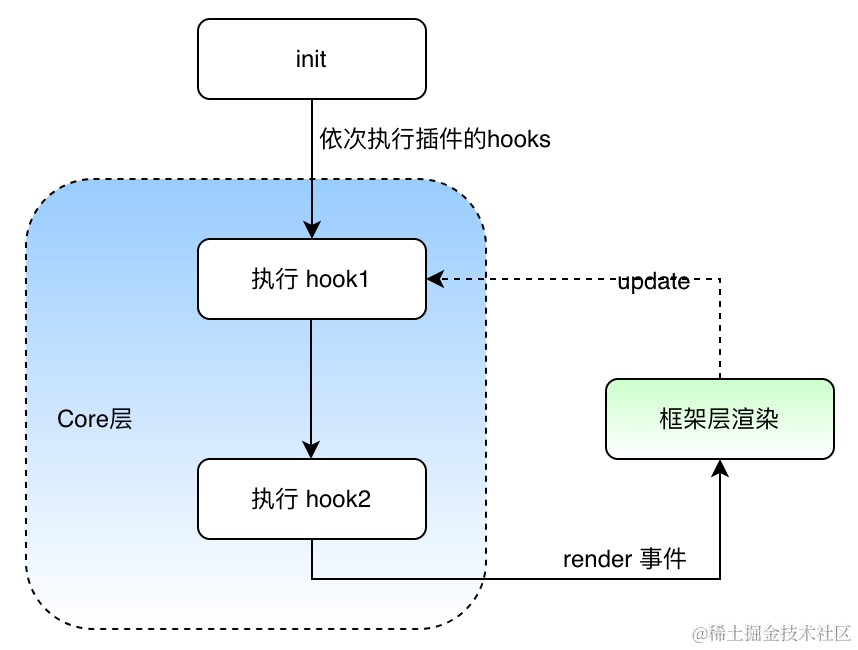
veImageX 演进之路:Web 图片加载提速50%
背景说明 火山引擎veImageX演进之路主要介绍了veImageX在字节内部从2012年随着字节成长过程中逐步演进的过程,演进中包括V1、V2、V3版本并最终面向行业输出;整个演进过程中包括服务端、客户端、网络库、业务场景与优化等多个角度介绍在图像处理压缩、省成…...
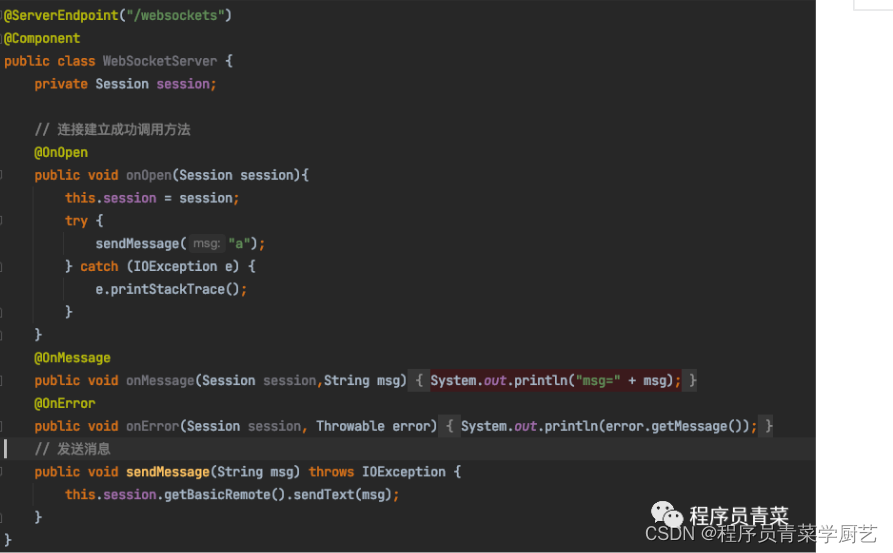
WebSocket实战之五JSR356
一、前言 前几篇WebSocket例子服务端我是用NodeJS实现,这一篇我们用Java来搭建一个WebSocket服务端,从2011年WebSocket协议RFC6455发布后,大多数浏览器都实现了WebSocket协议客户端的API,而对于服务端Java也定义了一个规范JSR356,即Java API for WebSoc…...

flask-sqlalchemy结合Blueprint遇到循环引入问题的解决方案
想要用flask_sqlalchemy结合Blueprint分模块写一下SQL的增删改查接口,结果发现有循环引入问题。 一开始,我在app.py中使用db SQLAlchemy(app)创建数据库对象;并且使用app.register_blueprint(db_bp, url_prefix/db)注册蓝图。 这使得我的依…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...


