第k小的数
补充习题: 第k小的数
问题描述
有两个正整数数列,元素个数分别为 N N N和 M M M.从两个数列中分别任取一个数相乘,这样一共可以得到 N × M N\times M N×M个数,询问这 N × M N\times M N×M个数中第 K K K小的数是多少.
- 数据范围:
N , M < = 200000 , K < = 2.1 ∗ 1 0 10 , A i < = 1 0 9 ; N,M<=200000,K<=2.1*10^{10},A_i<=10^9; N,M<=200000,K<=2.1∗1010,Ai<=109;
solution
∵ a > b , c > d \because a>b, c>d ∵a>b,c>d
∴ a × c > b × d \therefore a \times c > b \times d ∴a×c>b×d
设本题中的两个数组分别为 a 和 b 设本题中的两个数组分别为a和b 设本题中的两个数组分别为a和b
∴ 可知 , 若 a i × b j < K \therefore 可知,若a_i\times b_j < K ∴可知,若ai×bj<K
则 a i − 1 , i − 2 , . . . , 1 ∗ b j , j − 1 , . . . , 1 < K 则a_{i-1,i-2,...,1} * b_{j,j-1,...,1} < K 则ai−1,i−2,...,1∗bj,j−1,...,1<K
由此,这一题就好办了.
#include <bits/stdc++.h>
using namespace std;
int n, m, k;
int a[200001], b[200001];long long check(int x) {int i = 1;int j = m;long long sum = 0;while(j >= 1 && i <= n) {while(a[i] * b[j] > x) {--j;}sum += j;++i;}return sum;
}int main() {cin >> n >> m >> k;int max1 = -1, max2 = -1;for(int i = 1; i <= n; ++i) {cin >> a[i];max1 = max(max1, a[i]);}for(int i = 1; i <= m; ++i) {cin >> b[i];max2 = max(max2, b[i]);}sort(a + 1, a + n + 1);sort(b + 1, b + m + 1);long long l = 1, r = max1 * max2;long long ans = 0;while(l <= r) {long long mid = (l + r) >> 1;if(check(mid) >= k) {r = mid - 1;ans = mid;}else {l = mid + 1;}}cout << ans << endl;return 0;
}相关文章:

第k小的数
补充习题: 第k小的数 问题描述 有两个正整数数列,元素个数分别为 N N N和 M M M.从两个数列中分别任取一个数相乘,这样一共可以得到 N M N\times M NM个数,询问这 N M N\times M NM个数中第 K K K小的数是多少. 数据范围: N , M < 200000 , K < 2.1 ∗ 1 0 10 , …...
基于electron25+vite4创建多窗口|vue3+electron25新开模态窗体
在写这篇文章的时候,查看了下electron最新稳定版本由几天前24.4.0升级到了25了,不得不说electron团队迭代速度之快! 前几天有分享一篇electron24整合vite4全家桶技术构建桌面端vue3应用示例程序。 https://www.cnblogs.com/xiaoyan2017/p/17…...
红米手机 导出 通讯录 到电脑保存
不要搞什么 云服务 不要安装什么 手机助手 不要安装 什么app 用 usb 线 连接 手机 和 电脑 手机上会跳出 提示 选择 仅传输文件 会出现下面的 一个 盘 进入 MIUI目录 然后进入 此电脑\Redmi Note 5\内部存储设备\MIUI\backup\AllBackup\20230927_043337 如何没有上面的文件&a…...
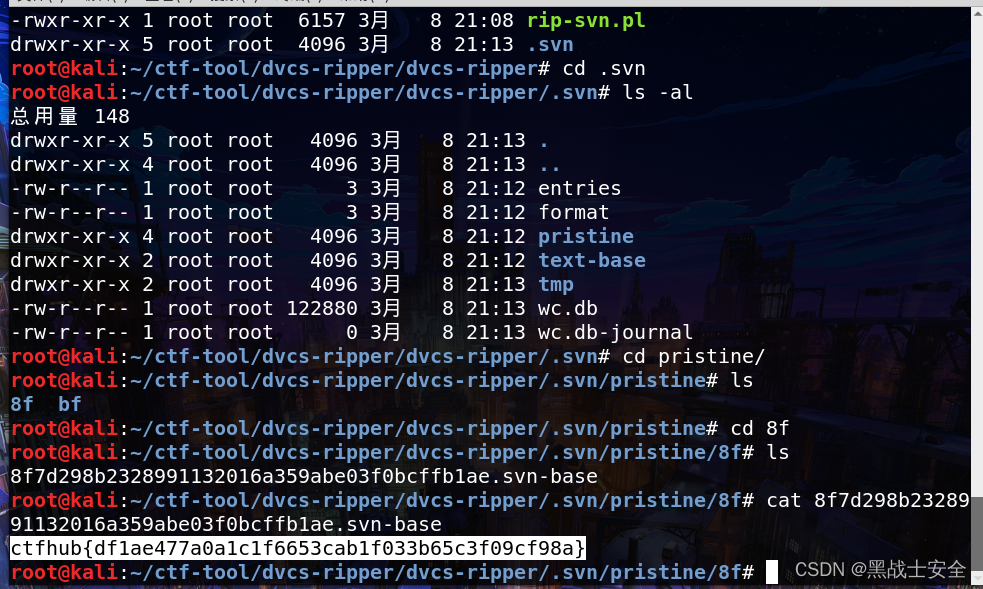
常见web信息泄露
一、源码(备份文件)泄露 1、git泄露 Git是一个开源的分布式版本控制系统,在执行git init初始化目录的时候,会在当前目录下自动创建一个.git目录,用来记录代码的变更记录等。发布代码的时候,如果没有把.git这个目录删除ÿ…...
找不到VCRUNTIME140_1.dll怎么办,VCRUNTIME140_1.dll丢失的5个解决方法
在当今的数字时代,我们的生活和工作都离不开电脑。然而,随着科技的发展,我们也会遇到各种各样的问题。其中,VCRUNTIME140_1.dll丢失的问题是许多人都会遇到的困扰。这个问题可能会导致许多应用程序无法正常运行,给我们…...

C#生成自定义海报
安装包 SixLabors.ImageSharp.Drawing 2.0 需要的字体:宋体和微软雅黑 商用的需要授权如果商业使用可以使用方正书宋、方正黑体,他们可以免费商用 方正官网 代码 using SixLabors.Fonts; using SixLabors.ImageSharp; using SixLabors.ImageSharp.Draw…...
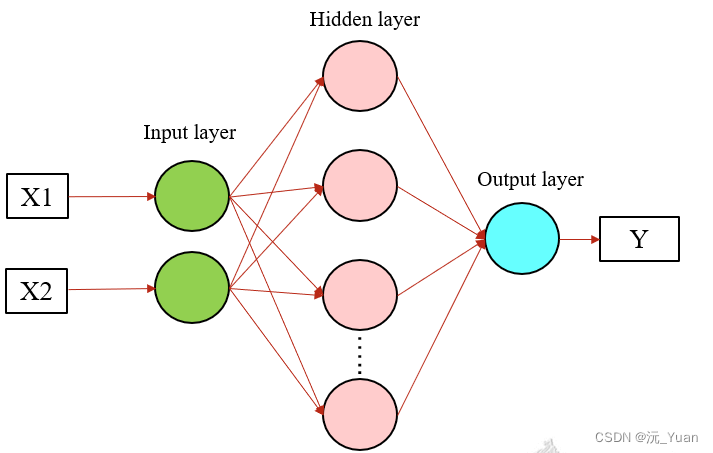
BP神经网络的MATLAB实现(含源代码)
BP(back propagation)神经网络是1986年由Rumelhart和McClelland为首的科学家提出的概念,是一种按照误差逆向传播算法训练的多层前馈神经网络,是应用最广泛的神经网络模型之一 具体数学推导以及原理在本文不做详细介绍,本文将使用MATLAB进行B…...

AES和Rijndael的区别
快速链接: . 👉👉👉 个人博客笔记导读目录(全部) 👈👈👈 付费专栏-付费课程 【购买须知】:密码学实践强化训练–【目录】 👈👈👈“Rijndael” 这个词的中文谐音可以近似地发音为 “瑞恩达尔”。请注意,这只是一种近似的发音方式,因为该词是荷兰姓氏 “Ri…...

【数据结构】—堆详解(手把手带你用C语言实现)
食用指南:本文在有C基础的情况下食用更佳 🔥这就不得不推荐此专栏了:C语言 ♈️今日夜电波:水星—今泉愛夏 1:10 ━━━━━━️💟──────── 4:23 …...

关于算法复杂度的几张表
算法在改进今天的计算机与古代的计算机的区别 去除冗余 数据点 算法复杂度 傅里叶变换...
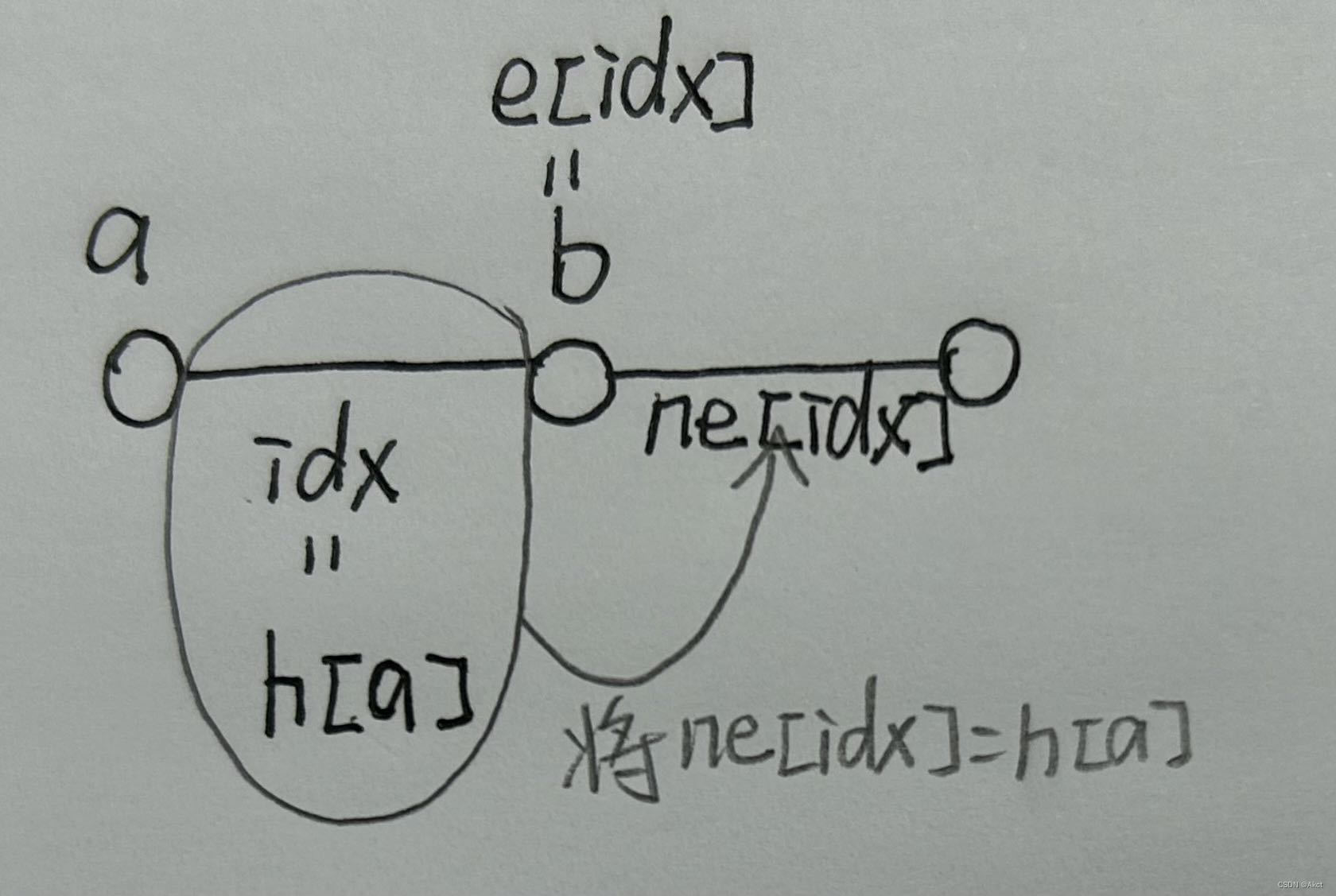
蓝桥杯每日一题2023.10.1
路径 - 蓝桥云课 (lanqiao.cn) 题目分析 求最短路问题,有多种解法,下面介绍两种蓝桥杯最常用到的两种解法 方法一 Floyd(求任意两点之间的最短路)注:不能有负权回路 初始化每个点到每个点的距离都为0x3f这样才能对…...
)
第三章:最新版零基础学习 PYTHON 教程(第十节 - Python 运算符—Python 中的运算符重载)
运算符重载意味着赋予超出其预定义操作含义的扩展含义。例如,运算符 + 用于添加两个整数以及连接两个字符串和合并两个列表。这是可以实现的,因为“+”运算符被 int 类和 str 类重载。您可能已经注意到,相同的内置运算符或函数对于不同类的对象显示不同的行为,这称为运算符…...
)
Nacos 实现服务平滑上下线(Ribbon 和 LB)
前言 不知道各位在使用 SpringCloud Gateway Nacos的时候有没有遇到过服务刚上线偶尔会出现一段时间的503 Service Unavailable,或者服务下线后,下线服务仍然被调用的问题。而以上问题都是由于Ribbon或者LoadBalancer的默认处理策略有关,其…...

c/c++里 对 共用体 union 的内存分配
对union 的内存分配,是按照最大的那个成员分配的。 谢谢...
博途SCL区间搜索指令(判断某个数属于某个区间)
S型速度曲线行车位置控制,停靠位置搜索功能会用到区间搜索指令,下面我们详细介绍区间搜索指令的相关应用。 S型加减速行车位置控制(支持点动和停车位置搜索)-CSDN博客S型加减速位置控制详细算法和应用场景介绍,请查看下面文章博客。本篇文章不再赘述,这里主要介绍点动动和…...
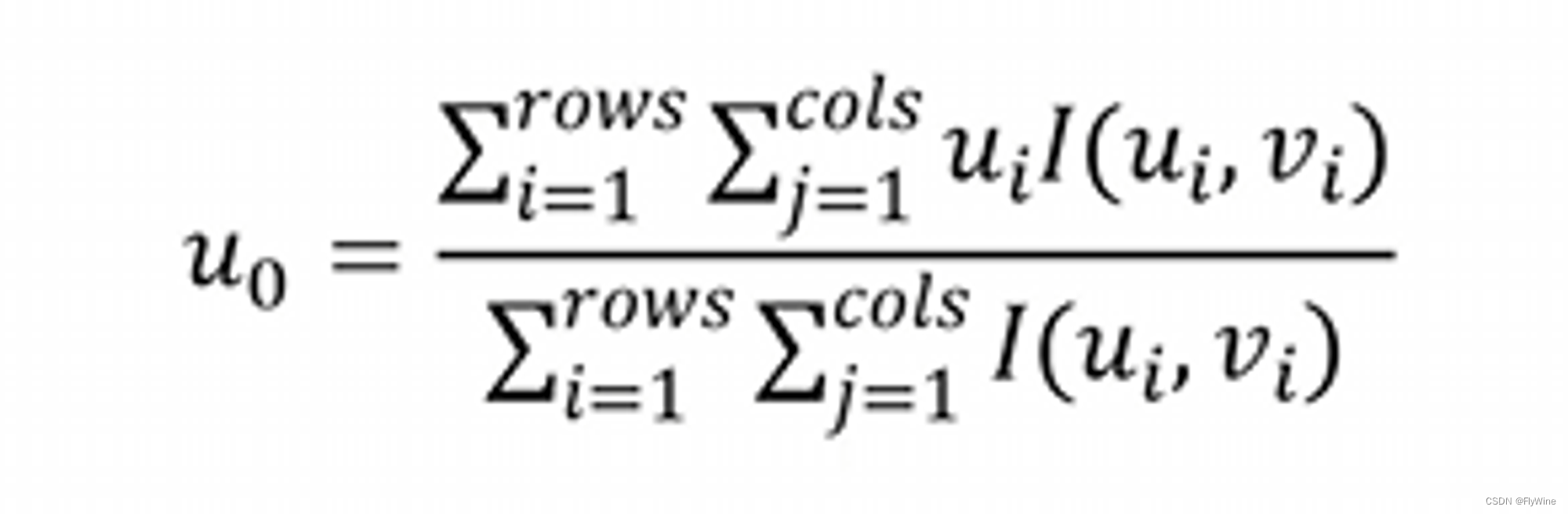
(三)激光线扫描-中心线提取
光条纹中心提取算法是决定线结构光三维重建精度以及光条纹轮廓定位准确性的重要因素。 1. 光条的高斯分布 激光线条和打手电筒一样,中间最亮,越像周围延申,光强越弱,这个规则符合高斯分布,如下图。 2. 传统光条纹中心提取算法 传统的光条纹中心提取算法有 灰度重心法、…...
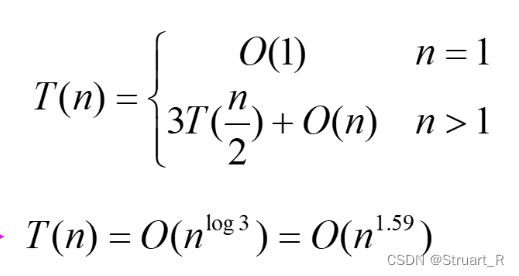
递归与分治算法(1)--经典递归、分治问题
目录 一、递归问题 1、斐波那契数列 2、汉诺塔问题 3、全排列问题 4、整数划分问题 二、递归式求解 1、代入法 2、递归树法 3、主定理法 三、 分治问题 1、二分搜索 2、大整数乘法 一、递归问题 1、斐波那契数列 斐波那契数列不用过多介绍,斐波那契提出…...
Java之SpringCloud Alibaba【六】【Alibaba微服务分布式事务组件—Seata】
一、事务简介 事务(Transaction)是访问并可能更新数据库中各种数据项的一个程序执行单元(unit)。 在关系数据库中,一个事务由一组SQL语句组成。 事务应该具有4个属性: 原子性、一致性、隔离性、持久性。这四个属性通常称为ACID特性。 原子性(atomicity) ∶个事务…...
Android逆向学习(五)app进行动态调试
Android逆向学习(五)app进行动态调试 一、写在前面 非常抱歉鸽了那么久,前一段时间一直在忙,现在终于结束了,可以继续更新android逆向系列的,这个系列我会尽力做下去,然后如果可以的话我看看能…...
音频编辑软件Steinberg SpectraLayers Pro mac中文软件介绍
Steinberg SpectraLayers Pro mac是一款专业的音频编辑软件,旨在帮助音频专业人士进行精细的音频编辑和声音处理。它提供了强大的频谱编辑功能,可以对音频文件进行深入的频谱分析和编辑。 Steinberg SpectraLayers Pro mac软件特点 1. 频谱编辑ÿ…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...
