【CFD小工坊】浅水方程的离散及求解方法
【CFD小工坊】浅水方程的离散及求解方法
- 前言
- 基于有限体积法的方程离散
- 界面通量与源项计算
- 干-湿网格的处理
- 数值离散的稳定性条件
- 参考文献
前言
我们模型的控制方程,即浅水方程组的表达式如下:
∂ U ∂ t + ∂ E ( U ) ∂ x + ∂ G ( U ) ∂ y = S ( U ) U = ( h h u h v ) , E ( U ) = ( h u h u 2 + g h 2 2 h u v ) , G ( U ) = ( h v h u v h v 2 + g h 2 2 ) , S ( U ) = ( 0 g h ( S 0 x − S f x ) g h ( S 0 y − S f y ) ) S 0 x = − ∂ z b ∂ x , S 0 y = − ∂ z b ∂ y S f x = n 2 u u 2 + v 2 h − 4 / 3 , S f y = n 2 v u 2 + v 2 h − 4 / 3 \dfrac{\partial \bold{U}}{\partial t} + \dfrac{\partial \bold{E(U)}}{\partial x} + \dfrac{\partial \bold{G(U)}}{\partial y} = \bold{S(U)} \\[6pt] \bold{U} = \left( \begin{matrix} h \\ hu \\ hv \end{matrix} \right), \bold{E(U)} = \left( \begin{matrix} hu \\ hu^2+\dfrac{gh^2}{2} \\ huv \end{matrix} \right), \bold{G(U)} = \left( \begin{matrix} hv \\ huv \\ hv^2+\dfrac{gh^2}{2} \end{matrix} \right), \\[6pt] \bold{S(U)} = \left( \begin{matrix} 0 \\ gh(S_{0x} - S_{fx}) \\ gh(S_{0y} - S_{fy}) \end{matrix} \right) \\[6pt] S_{0x} = -\dfrac{\partial z_b}{\partial x}, S_{0y} = -\dfrac{\partial z_b}{\partial y} \\[6pt] S_{fx} = n^2 u \sqrt{u^2+v^2} h^{-4/3}, S_{fy} = n^2 v \sqrt{u^2+v^2} h^{-4/3} ∂t∂U+∂x∂E(U)+∂y∂G(U)=S(U)U= hhuhv ,E(U)= huhu2+2gh2huv ,G(U)= hvhuvhv2+2gh2 ,S(U)= 0gh(S0x−Sfx)gh(S0y−Sfy) S0x=−∂x∂zb,S0y=−∂y∂zbSfx=n2uu2+v2h−4/3,Sfy=n2vu2+v2h−4/3
对此,我们首先将式中物理量离散于三角形网格中,后采用有限体积法将浅水方程改写成其离散形式。在离散的浅水方程中,水位、流速等物理量的计算可转化为对网格界面的通量项和网格内源项的计算。对于离散方程中的通量项,本模型将会采用基于Riemann近似解的Roe格式数值求解界面通量。
基于有限体积法的方程离散
对于我们的浅水模型,水深、流速等物理量被定义在网格中心,如下图所示。对于网格i与j,它们间的质量、动量传输是通过其网格边界Ei,j发生的(下图中加粗的网格边)。网格i和j之间边界的外法相量定义为n=(nx, ny)。
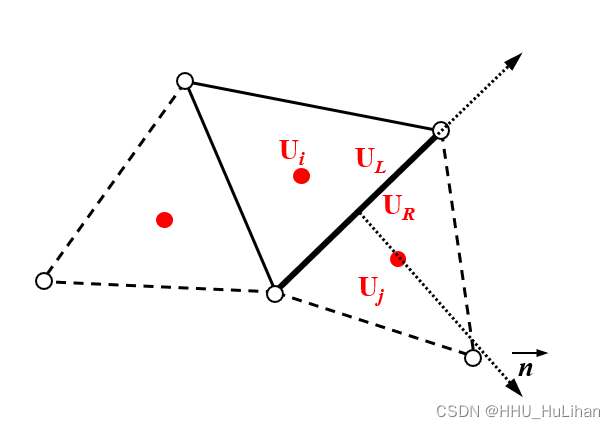
之后,对于控制体网格i,我们采用高斯散度定理将浅水方程沿着边界Ei,j线积分,得到:
∬ Ω ∂ U ∂ t d Ω = − ∫ S [ E ( U ) n x + G ( U ) n y ] d s + ∬ Ω S ( U ) d Ω \iint_{\Omega} \dfrac{\partial \bold{U}}{\partial t} d\Omega = -\int_{S} [\bold{E(U)}n_x + \bold{G(U)}n_y] ds + \iint_{\Omega} \bold{S(U)} d\Omega ∬Ω∂t∂UdΩ=−∫S[E(U)nx+G(U)ny]ds+∬ΩS(U)dΩ
式中,Ω表示网格i所对应的控制体,S表示边界Ei,j;dΩ和ds分别表示面积分和线积分的微元。
在我们的模型中,各个水力要素在网格体内被假定是均匀分布的。在对上式的时间导数项采用前差格式离散,得到数值解为:
U i n + 1 = U i n − Δ t Ω i ∑ j = 1 3 F n j L j + Δ t S ˉ F n = E ( U ) n x + G ( U ) n y \bold{U}_{i}^{n+1} = \bold{U}_{i}^{n} - \dfrac{\Delta t}{\Omega_i} \sum_{j=1}^{3} \bold{F}_{nj}L_j + \Delta t \bar{S} \\[6pt] \bold{F_n} = \bold{E(U)}n_x + \bold{G(U)}n_y Uin+1=Uin−ΩiΔtj=1∑3FnjLj+ΔtSˉFn=E(U)nx+G(U)ny
其中,Δt为时间步长,Ωi表示网格单元i的面积,Fnj表示网格i中第j条边的外通量,Lj表示网格i中第j条边的长度;S表示源项, S ˉ \bar{S} Sˉ表示源项S在网格i的体积分值。
注意,上式就是模型求解过程中最核心的表达式。它完成了从该时间步水力变量到下一步水力变量的更新计算。
界面通量与源项计算
接下来要解决的问题是通量项 F n \bold{F_n} Fn的计算。首先,我们将网格边通量计算转化为一个Riemann近似解问题。采用Roe格式来求解这个近似黎曼解:
F n = 1 2 ( E ( U ~ L ) + G ( U ~ R ) ) − ∑ k = 1 3 α ~ k ∣ λ k ∣ γ k ) \bold{F_n} = \dfrac{1}{2} (\bold{E(\tilde{U}_L)} + \bold{G(\tilde{U}_R))} - \sum_{k=1}^{3} \tilde{\alpha}^k |\lambda^k| \gamma^k) Fn=21(E(U~L)+G(U~R))−k=1∑3α~k∣λk∣γk)
式中, λ k \lambda^k λk为基于 Roe 平均的雅克比矩阵 J J J的特征值, γ k \gamma^k γk为特征值对应的特征向量; α k \alpha^k αk表示特征强度。各项表达如下:
{ λ 1 = u ~ − c ~ λ 2 = u ~ λ 3 = u ~ + c ~ , { γ 1 = ( 1 , u − c ~ , v ~ ) T γ 2 = ( 0 , 0 , 1 ) T γ 3 = ( 1 , u + c ~ , v ~ ) T , { α ~ 1 = 1 2 [ h R − h L − h ~ c ~ ( u R − u L ) ] α ~ 2 = h ~ ( v R − v L ) α ~ 3 = 1 2 [ h R − h L + h ~ c ~ ( u R − u L ) ] \left\{ \begin{aligned} \lambda^1 & = \tilde u-\tilde{c} \\ \lambda^2 & = \tilde u \\ \lambda^3 & = \tilde u+\tilde{c} \end{aligned} \right. , \left\{ \begin{aligned} \gamma^1 & = (1, u-\tilde{c}, \tilde{v})^T \\ \gamma^2 & = (0,0,1)^T \\ \gamma^3 & = (1, u+\tilde{c}, \tilde{v})^T \end{aligned} \right. , \left\{ \begin{aligned} \tilde \alpha^1 & = \dfrac{1}{2}[h_R - h_L - \dfrac{\tilde h}{\tilde{c}}(u_R- u_L)] \\ \tilde \alpha^2 & = \tilde h (v_R - v_L) \\ \tilde \alpha^3 & = \dfrac{1}{2}[h_R - h_L + \dfrac{\tilde h}{\tilde{c}}(u_R- u_L)] \end{aligned} \right. ⎩ ⎨ ⎧λ1λ2λ3=u~−c~=u~=u~+c~,⎩ ⎨ ⎧γ1γ2γ3=(1,u−c~,v~)T=(0,0,1)T=(1,u+c~,v~)T,⎩ ⎨ ⎧α~1α~2α~3=21[hR−hL−c~h~(uR−uL)]=h~(vR−vL)=21[hR−hL+c~h~(uR−uL)]
上述变量中下标L和R分别表示该变量是边界内、外侧网格上的值(如上图所示); u ~ \tilde u u~、 v ~ \tilde v v~、 c ~ \tilde{c} c~和 h ~ \tilde h h~都是Roe平均变量,定义如下:
u ~ = u L h L + u R h R h L + h R , v ~ = v L h L + v R h R h L + h R , c ~ = g ( h L + h R ) 2 , h ~ = h L h R \tilde{u} = \dfrac{u_L \sqrt{h_L} + u_R \sqrt{h_R}}{\sqrt{h_L} + \sqrt{h_R}}, \tilde{v} = \dfrac{v_L \sqrt{h_L} + v_R \sqrt{h_R}}{\sqrt{h_L} + \sqrt{h_R}}, \\[6pt] \tilde c = \sqrt{\dfrac{g(h_L + h_R)}{2}}, \tilde h=\sqrt{h_L h_R} u~=hL+hRuLhL+uRhR,v~=hL+hRvLhL+vRhR,c~=2g(hL+hR),h~=hLhR
注意,此处下标含L和R的速度 u ~ \tilde u u~均是垂直于网格边(与外法向n同向)的速度分量,且波速c的方向也与外法向n同向。同理,下标含L和R的 v ~ \tilde v v~则是与法相量n相垂直。
此外,对源项S中的底坡和摩阻项的处理将直接关系到模型的计算精度和稳定性。为了获得和谐、守恒的结果,对底坡源项进行特征分解和迎风处理以适应Riemann求解格式。首先,对底坡源项在控制体Ω内积分得到 S ˉ 0 \bar{S}_0 Sˉ0:
S ˉ 0 = ∑ j = 0 3 ∑ k = 0 3 [ 1 2 ( 1 − s i g n ( λ k ˉ ) ) ( β k r k ˉ ) L j ] j ( β 1 , β 2 , β 3 ) = ( − 1 2 c ~ Δ z b , 0 , 1 2 c ~ Δ z b ) , Δ z b = ( z b ) L − ( z b ) R r 1 ˉ = ( 1 u ~ + c ~ v ~ ) , r 2 ˉ = ( 0 0 c ~ ) , r 3 ˉ = ( 1 u ~ − c ~ v ~ ) , \bar{S}_0 = \sum_{j=0}^{3} \sum_{k=0}^{3} [\dfrac{1}{2} (1-sign(\bar{\lambda^k})) ({\beta^k} \bar{r^k}) L_{j}]^j \\[6pt] (\beta^1,\beta^2,\beta^3)= (-\dfrac{1}{2}\tilde{c}\Delta{z_b}, 0 , \dfrac{1}{2}\tilde{c}\Delta{z_b}), \Delta{z_b} = (z_b)_L - (z_b)_R \\[6pt] \bar{r^1}= \left( \begin{matrix} 1 \\ \tilde{u} + \tilde{c} \\ \tilde{v} \end{matrix} \right), \bar{r^2}= \left( \begin{matrix} 0 \\ 0 \\ \tilde{c} \end{matrix} \right), \bar{r^3}= \left( \begin{matrix} 1 \\ \tilde{u} - \tilde{c} \\ \tilde{v} \end{matrix} \right), Sˉ0=j=0∑3k=0∑3[21(1−sign(λkˉ))(βkrkˉ)Lj]j(β1,β2,β3)=(−21c~Δzb,0,21c~Δzb),Δzb=(zb)L−(zb)Rr1ˉ= 1u~+c~v~ ,r2ˉ= 00c~ ,r3ˉ= 1u~−c~v~ ,
式中,sign( )为符号函数。
为增加格式的稳定性,对摩阻源项进行半隐式离散,其表达式为:
S f = ( 1 − θ ) S f n + θ S f n + 1 = S f n + θ ∂ S f ∂ U ∂ U ∂ t Δ t \bold{S}_f = (1-\theta) \bold{S}_f^{n} + \theta \bold{S}_f^{n+1} = \bold{S}_f^{n} + \theta \dfrac{\partial \bold{S}_f}{\partial \bold{U}} \dfrac{\partial \bold{U}}{\partial t} \Delta t Sf=(1−θ)Sfn+θSfn+1=Sfn+θ∂U∂Sf∂t∂UΔt
θ=0时意味着完全显式,θ=1时意味着完全隐式;令 Q f = ∂ S f ∂ U \bold{Q}_f = \dfrac{\partial \bold{S}_f}{\partial \bold{U}} Qf=∂U∂Sf,离散后的动量方程通量表达式为:
Δ U = U n + 1 − U n = [ I − Δ t θ Q f n ] − 1 [ Δ t Ω i ∑ j = 1 3 ( F n j + ∑ k = 0 3 [ 1 2 ( 1 − s i g n ( λ k ˉ ) ) ( β k r k ˉ ) ) L j + Δ t S f ] \Delta \bold{U} = \bold{U}^{n+1} - \bold{U}^{n} = [\bold{I}- \Delta t \theta \bold{Q}_f ^{n}]^{-1} [\dfrac{\Delta t}{\Omega_i} \sum_{j=1}^{3} (\bold{F}_{nj} +\sum_{k=0}^{3} [\dfrac{1}{2} (1-sign(\bar{\lambda^k})) ({\beta^k} \bar{r^k}) )L_j + \Delta t \bold{S}_f] ΔU=Un+1−Un=[I−ΔtθQfn]−1[ΩiΔtj=1∑3(Fnj+k=0∑3[21(1−sign(λkˉ))(βkrkˉ))Lj+ΔtSf]
干-湿网格的处理
对于复杂的地形,计算区域内的实际模拟范围和计算边界变化频繁。网格上可能出现淹没-干底-再淹没的过程,这对模型的计算提出较高的稳定性要求。为避免水深较小时网格=出现流速过大的非物理现象,本模型采用限制水深法来准确、稳定地模拟网格淹没、干底这一过程。
首先,设置两个临界水深 h d r y h_{dry} hdry和 h w e t h_{wet} hwet(且 h d r y < h w e t h_{dry}<h_{wet} hdry<hwet),再将网格分为三类:
- 当水深大于 h w e t h_{wet} hwet,该网格为“湿网格”,参与正常的模拟计算,同时求解质量和动量通量;
- 当水深小于 h d r y h_{dry} hdry,该网格为“干网格”,不参与当前时间步的计算;
- 当水深在 h d r y h_{dry} hdry和 h w e t h_{wet} hwet之间,该网格为“半干网格”,仅计算该时间步的质量通量,而没有计算动量通量。
数值离散的稳定性条件
本模型基于Riemann显式方法,即当前时刻的网格变量可直接由上一时刻的计算结果得到,无需经过迭代计算。但显式求解法受到CFL条件的限制,实际计算过程中的最大时间步长通常不为定值。
本模型将采用动态时间步长方法得到模拟的时间步长;同时需要用户输入一个可允许的最大步长 Δ t m a x \Delta t_{max} Δtmax,以及一个允许的最大Courant数 C m a x C_{max} Cmax( 0 < C < 1.0 0< C <1.0 0<C<1.0)。模型的时间步长按下式确定:
Δ t = m i n ( Δ t m a x , C m a x m i n ( R i u i 2 + v i 2 + g h i ) ) , i = 1 , 2 , 3 , . . . , N c \Delta t = min(\Delta t_{max}, C_{max} min(\dfrac{R_i}{\sqrt{u^2_i + v^2_i} + \sqrt{gh_i}})), i=1,2,3,...,N_c Δt=min(Δtmax,Cmaxmin(ui2+vi2+ghiRi)),i=1,2,3,...,Nc
参考文献
- 刘臻,史宏达,黄燕.一种基于Roe格式的有限体积法在二维溃坝问题中的应用[J].中国海洋大学学报:自然科学版, 2007, 37(2):5.
- [王志力,耿艳芬,金生.具有复杂计算域和地形的二维浅水流动数值模拟[J].水利学报, 2005, 36(4):6.
相关文章:

【CFD小工坊】浅水方程的离散及求解方法
【CFD小工坊】浅水方程的离散及求解方法 前言基于有限体积法的方程离散界面通量与源项计算干-湿网格的处理数值离散的稳定性条件参考文献 前言 我们模型的控制方程,即浅水方程组的表达式如下: ∂ U ∂ t ∂ E ( U ) ∂ x ∂ G ( U ) ∂ y S ( U ) U…...

第十四章 类和对象——C++对象模型和this指针
一、成员变量和成员函数分开存储 在C中,类内的成员变量和成员函数分开存储 只有非静态成员变量才属于类的对象上 class Person {public:Person() {mA 0;}//非静态成员变量占对象空间int mA;//静态成员变量不占对象空间static int mB; //函数也不占对象空间&#…...

计算机竞赛 深度学习卫星遥感图像检测与识别 -opencv python 目标检测
文章目录 0 前言1 课题背景2 实现效果3 Yolov5算法4 数据处理和训练5 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 **深度学习卫星遥感图像检测与识别 ** 该项目较为新颖,适合作为竞赛课题方向,学长非常推荐…...
java web+Mysql e-life智能生活小区物业管理系统
本项目为本人自己书写,主要服务小区业主和管理人员。 e-life智能生活小区涉及多个方面的智能化和便利化服务: 1. 用户模块:包含基本的登入登出操作,查看个人信息中用户可以查看 自己的个人资料但不可以修改个人信息。 a) 用户…...

AttributeError: module ‘dgl‘ has no attribute ‘batch_hetero‘
DGLWarning: From v0.5, DGLHeteroGraph is merged into DGLGraph. You can safely replace dgl.batch_hetero with dgl.batch...
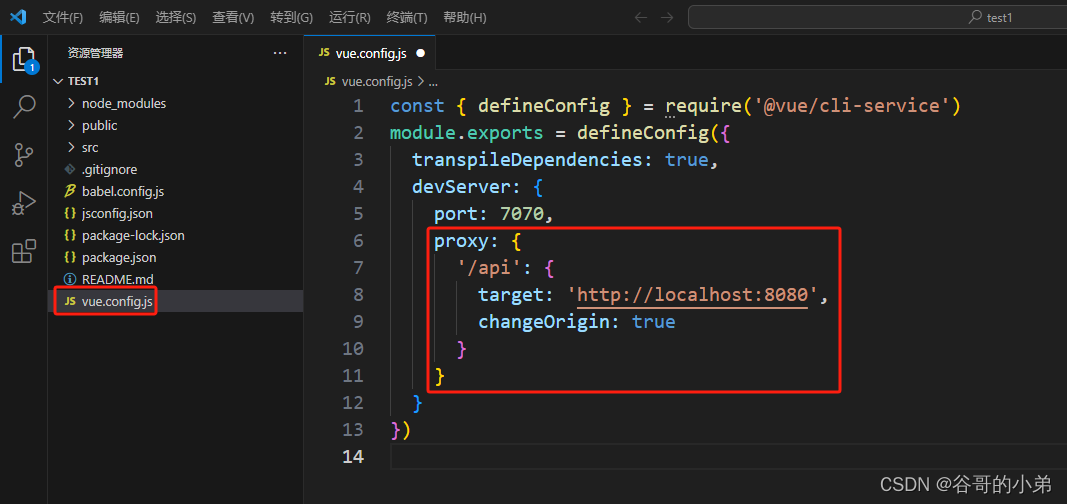
Vue项目搭建图文详解教程
版权声明 本文原创作者:谷哥的小弟作者博客地址:http://blog.csdn.net/lfdfhl 预备工作 请在本地创建文件夹用于存放Vue项目,例如:创建HelloWorld文件夹存放即将创建的Vue新项目。 创建Vue项目 首先,请在DOS中将目录…...

SpringMVC处理请求核心流程
一、前言 SpringMVC是一个基于Java的Web框架,它使用MVC(Model-View-Controller)设计模式来处理Web请求。在SpringMVC中,请求处理的核心流程主要包括以下几个步骤: 1、用户发送请求到前端控制器(Dispatche…...

SoloX:Android和iOS性能数据的实时采集工具
SoloX:Android和iOS性能数据的实时采集工具 github地址:https://github.com/smart-test-ti/SoloX 最新版本:V2.7.6 一、SoloX简介 SoloX是开源的Android/iOS性能数据的实时采集工具,目前主要功能特点: 无需ROOT/越狱…...

【知识点随笔分析 | 第五篇】简单介绍什么是QUIC
前言: 随着互联网的快速发展,传统的基于TCP的协议开始显现出一些局限性。TCP在连接建立和拥塞控制方面存在一定的延迟,这可能导致用户在访问网页、观看视频或玩网络游戏时感受到不必要的等待时间。而QUIC作为一种新兴的传输协议,试…...

vscode ssh 远程免密登录开发
存放代码的机器运行 sshd, vscode 所在机器保证可以通过 ssh 登录服务器vscode 机器通过 ssh-keygen 生成 ssh 公私钥对(已有可以忽略)将客户端的 id_rsa.pub 加入到服务器的鉴权队列 cat id_rsa.pub >> authorized_keysvscode 配置ssh登录即可.ctrlp, remote-ssh: open …...
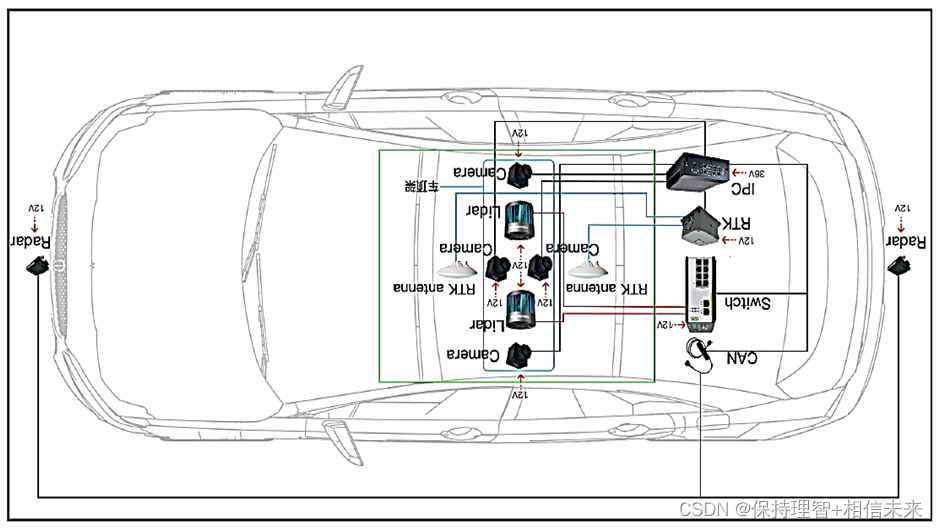
辅助驾驶功能开发-测试篇(2)-真值系统介绍
1 真值系统概述 1.1 真值评测系统核心应用 快速构建有效感知真值,快速完成感知性能评估,快速分析感知性能缺陷。 主要应用场景包括: 1. 感知算法开发验证: 在算法开发周期中,评测结果可以作为测试报告的一部分,体现算法性能的提升。 2. 遴选供应…...

运行程序时msvcr110.dll丢失的解决方法,msvcr110.dll丢失5的个详细解决方法
在使用电脑的过程中,我们经常会遇到各种问题,其中之一就是 msvcr110.dll 丢失的问题。msvcr110.dll 是 Microsoft Visual C Redistributable 的一个组件,用于支持使用 Visual C 编写的应用程序。如果您的系统中丢失了这个文件,您可…...

已解决 Bug——IndexError: index 3 is out of bounds for axis 0 with size 3问题
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页: 🐅🐾猫头虎的博客🎐《面试题大全专栏》 🦕 文章图文并茂🦖…...
WEB3 solidity 带着大家编写测试代码 操作订单 创建/取消/填充操作
好 在我们的不懈努力之下 交易所中的三种订单函数已经写出来了 但是 我们只是编译 确认了 代码没什么问题 但还没有实际的测试过 这个测试做起来 其实就比较的麻烦了 首先要有两个账号 且他们都要在交易所中有存入 我们还是先将 ganache 的虚拟环境启动起来 然后 我们在项目…...
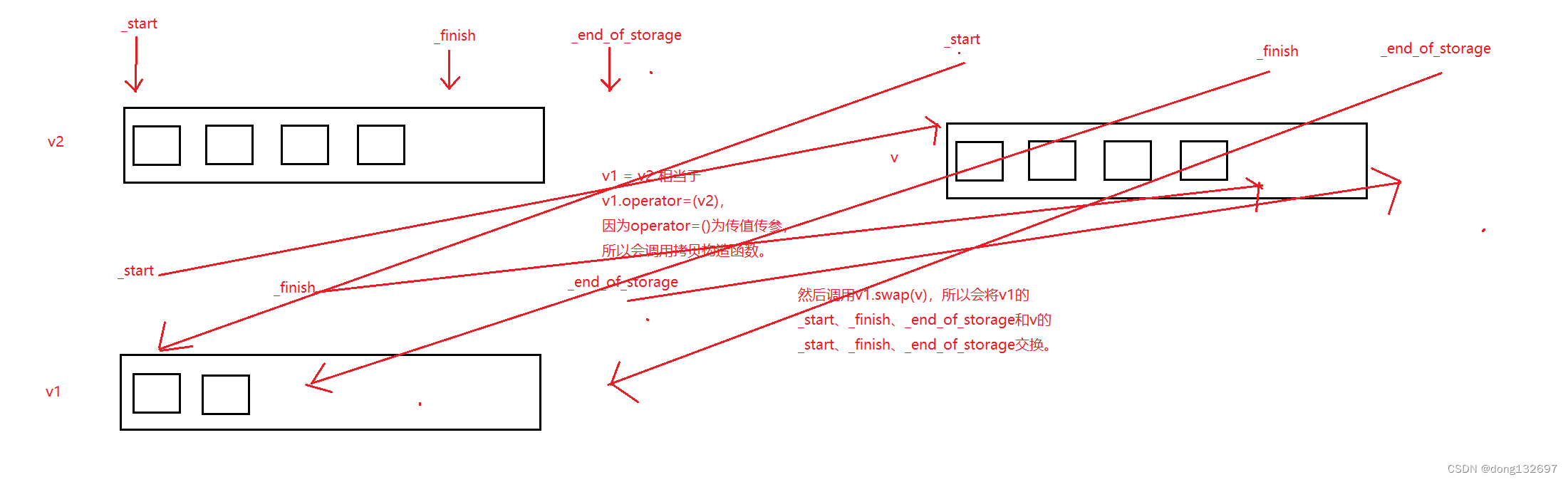
c++-vector
文章目录 前言一、vector介绍二、vector使用1、构造函数2、vector 元素访问3、vector iterator 的使用4、vector 空间增长问题5、vector 增删查改6、理解vector<vector< int >>7、电话号码的字母组合练习题 三、模拟实现vector1、查看STL库源码中怎样实现的vector2…...
十四天学会C++之第二天(函数和库)
1. 函数的定义和调用 在C中,函数是组织和结构化代码的关键工具之一。它们允许您将一段代码封装成一个可重复使用的模块,这有助于提高代码的可读性和维护性。 为什么使用函数? 函数在编程中的作用不可小觑。它们有以下几个重要用途…...

蓝桥杯每日一题2023.10.3
杨辉三角形 - 蓝桥云课 (lanqiao.cn) 题目描述 题目分析 40分写法: 可以自己手动构造一个杨辉三角,然后进行循环,用cnt记录下循环数的个数,看哪个数与要找的数一样,输出cnt #include<bits/stdc.h> using na…...

JavaScript系列从入门到精通系列第十二篇:JavaScript中对象的简介和对象的基本操作以及JavaScript中的属性值和属性名
文章目录 前言 一:对象分类 1:内建对象 2:宿主对象 3:自建对象 二:对象的基本操作 1:创建对象 2:向对象中添加属性 3:读取对象中的属性 4:修改对象中的属性 三…...
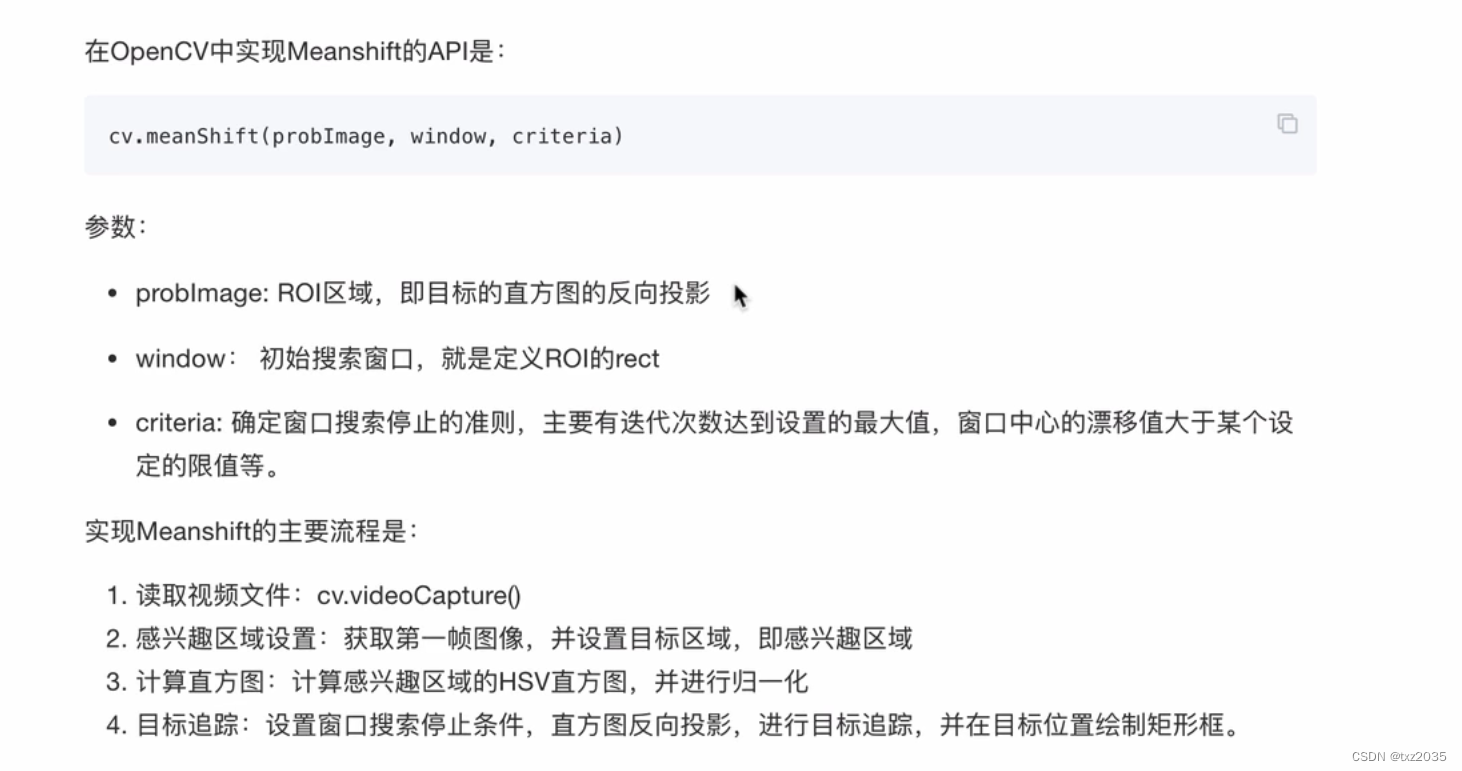
OpenCV实现视频的追踪(meanshift、Camshift)
目录 1,meanshift 1.1 算法流程 1.2 算法实现 1.3 代码实现 1.4 结果展示 1,meanshift 1.1 算法流程 1.2 算法实现 1.3 代码实现 import numpy as np import cv2 as cv# 读取视频 cap cv.VideoCapture(video.mp4)# 检查视频是否成功打开 if n…...

并查集详解(原理+代码实现+应用)
文章目录 1. 并查集概念2. 并查集原理2.1 合并2.1 找根 3. 并查集实现3.1 结构定义3.2 FindRoot(找根)3.3 Union(合并)3.4 IsInSet(判断两个值是否在一个集合里)3.5 SetCount(并查集中集合个数&…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...
