当前位置： 首页 > news >正文

mstsc无法保存RDP凭据, 100%生效

news 2026/2/9 22:10:32

问题

即使如下两项都打勾，其还是无法保存凭据，特别是连接Ubuntu (freerdp server)：
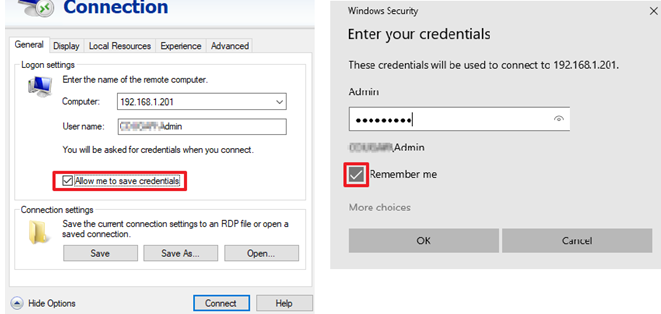
在这里插入图片描述

解决方法

网上多种复杂方法，不生效，其思路是修改后台配置，以使mstsc跟平常一样自动记住凭据。最后，如下的思路方法，最靠谱，即去Credential Manager中手动添加凭据。

  1. 在控制面板中打开凭据管理器

  2. 选择添加通用凭证

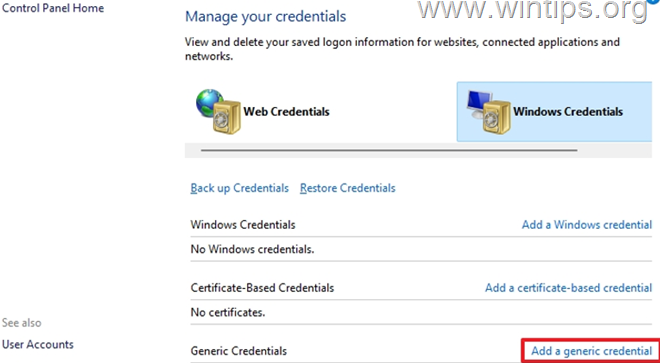
在这里插入图片描述

  1. 在“因特网或网络地址”字段中，键入 TERMSRV/，然后输入远程计算机的名称或 IP 地址。然后键入 RDP 连接的用户名和密码，然后单击“确定”。
    *注意：互联网或网络地址必须以 TERMSRV/ 开头，后跟 PC 名称或 IP 地址。e…g “TERMSRV/10.199.212.49”。
    在这里插入图片描述
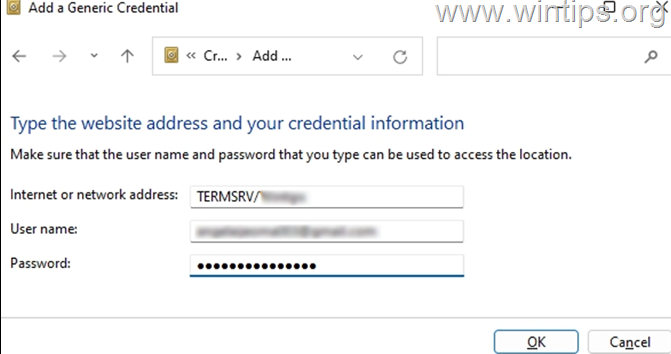
  2. 关闭凭据管理器并连接到 RDP。

相关文章：

mstsc无法保存RDP凭据, 100%生效

问题 即使如下两项都打勾，其还是无法保存凭据，特别是连接Ubuntu (freerdp server)： 解决方法 网上多种复杂方法，不生效，其思路是修改后台配置，以使mstsc跟平常一样自动记住凭据。最后，如下的…...

编程日记 2023/10/4 14:26:25

OpenGLES：绘制一个混色旋转的3D球体

效果展示 本篇博文会实现一个混色旋转的3D球体 一.球体解析 前面几篇博文讲解了如何使用OpenGLES实现不同的3D图形 本篇博文讲解怎样实现3D世界的代表图形：一个混色旋转的3D球体 1.1 极限正多面体 如果有学习过我前几篇3D图形绘制的博文，就知道要想…...

编程日记 2023/10/4 14:21:20

Spring AOP 基于注解源码整理

导入配置类 EnableAspectJAutoProxy 注解导入 AspectJAutoProxyRegistrarImportBeanDefinitionRegistrar#registerBeanDefinitions向容器中加入AnnotationAwareAspectJAutoProxyCreatorAnnotationAwareAspectJAutoProxyCreator#initBeanFactory初始化ReflectiveAspectJAdvisor…...

编程日记 2023/10/4 14:16:15

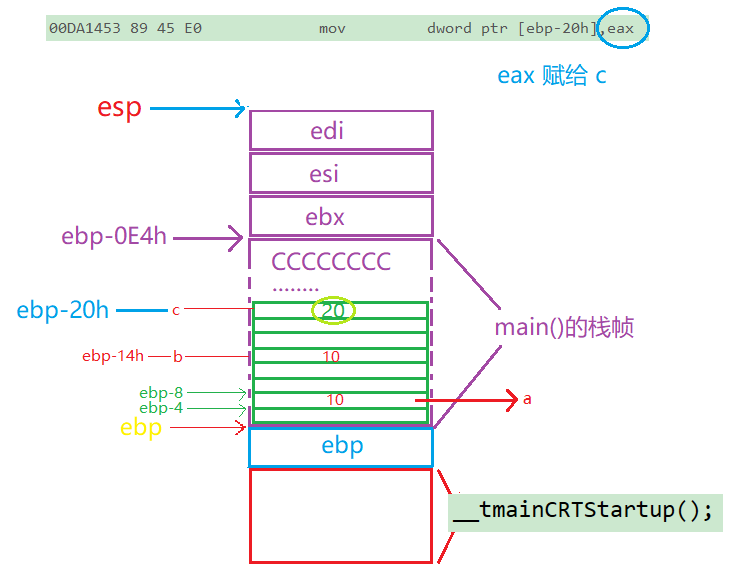
C语言 —— 函数栈帧的创建和销毁

在我们之前学习函数的时候，我们可能有很多困惑? 比如: 局部变量是怎么创建的?为什么局部变量的值是随机值?函数是怎么传参的?传参的顺序是怎样的?形参和实参是什么关系?函数调用是怎么做的?函数调用是结束后怎么返回的? 那么要解决这些问题, 我们就需要知道…...

编程日记 2023/10/4 14:15:15

Appleid苹果账号自动解锁改密（自动解锁二验改密码）

目前该项目能实现以下功能： 多用户使用，权限控制多账号管理账号分享页，支持设置密码、有效期、自定义HTML内容自动解锁与关闭二步验证自动/定时修改密码自动删除Apple ID中的设备代理池与Selenium集群，提高解锁成功率允许手动触发…...

编程日记 2023/10/4 14:12:12

Conflicting peer dependency: eslint@8.50.0

npm install 输出 npm ERR! code ERESOLVE npm ERR! ERESOLVE could not resolve npm ERR! npm ERR! While resolving: vue/eslint-config-standard6.1.0 npm ERR! Found: eslint-plugin-vue8.7.1 npm ERR! node_modules/eslint-plugin-vue npm ERR! dev eslint-plugin-vue…...

编程日记 2023/10/4 14:09:08

Vue3 defineProps使用

MyTag.vue <script setup> import { ref, nextTick, defineProps, defineEmits } from "vue"; const props defineProps({flag: Boolean,title: String, }); // 写成这样也可以 // const props defineProps(["flag", "title"]);const e…...

编程日记 2023/10/4 14:06:05

机器学习7：逻辑回归

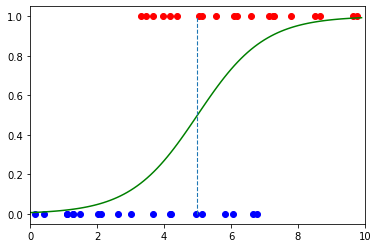
一、说明 逻辑回归模型是处理分类问题的最常见机器学习模型之一。二项式逻辑回归只是逻辑回归模型的一种类型。它指的是两个变量的分类&#xff0c;其中概率用于确定二元结果&#xff0c;因此“二项式”中的“bi”。结果为真或假 — 0 或 1。 二项式逻辑回归的一个例子是预测人…...

编程日记 2023/10/4 14:05:04

生活小记-纸张尺寸

A系列纸张&#xff1a; A0&#xff1a;841 x 1189 毫米A1&#xff1a;594 x 841 毫米A2&#xff1a;420 x 594 毫米A3&#xff1a;297 x 420 毫米A4&#xff1a;210 x 297 毫米A5&#xff1a;148 x 210 毫米A6&#xff1a;105 x 148 毫米A7&#xff1a;74 x 105 毫米A8&#xf…...

编程日记 2023/10/4 14:04:02

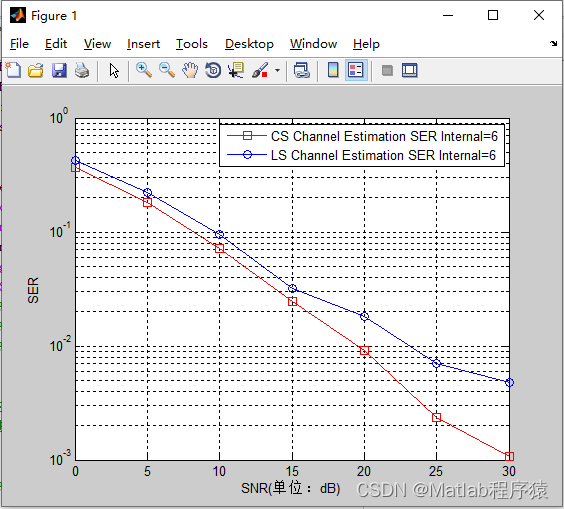
【MATLAB源码-第41期】基于压缩感知算法的OFDM系统信道估计和LS算法对比仿真。

操作环境&#xff1a; MATLAB 2013b 1、算法描述 压缩感知&#xff08;Compressed Sensing, CS&#xff09;是一种从稀疏或可压缩信号中重构完整信号的数学理论和技术。下面详细介绍压缩感知和它在OFDM信道估计中的应用。 1. 压缩感知基本概念 在传统采样理论中&#xff0…...

编程日记 2023/10/4 14:03:01

优思学院｜六西格玛将烹饪和美味提升至极致

最近&#xff0c;我们曾提到一个美国男子如何利用六西格玛来控制糖尿病。这表明六西格玛逐渐被认为是一个不仅可以在工作场所之外使用&#xff0c;尤其不仅限于制造业的系统。 六西格玛的核心理念是改进过程的质量&#xff0c;从而改善最终结果。如果你做了晚餐或尝试了一道新…...

编程日记 2023/10/4 14:00:59

git stash

git stash 是 Git 中一个非常有用的命令&#xff0c;用于临时保存当前工作目录中的修改&#xff0c;以便你可以切换到其他分支或处理其他任务而不丢失你的修改。它的主要用途是&#xff1a; 保存未提交的修改&#xff1a;你可以使用 git stash 命令将未提交的修改&#xff08;包…...

编程日记 2023/10/4 13:57:57

Flink Data Source

Flink Data Source 一、内置 Data Source Flink Data Source 用于定义 Flink 程序的数据来源，Flink 官方提供了多种数据获取方法，用于帮助开发者简单快速地构建输入流，具体如下： 1.1 基于文件构建 1. readTextFile(path)：按照 TextInputFormat 格式读取文本文件，并将…...

编程日记 2023/10/4 13:55:55

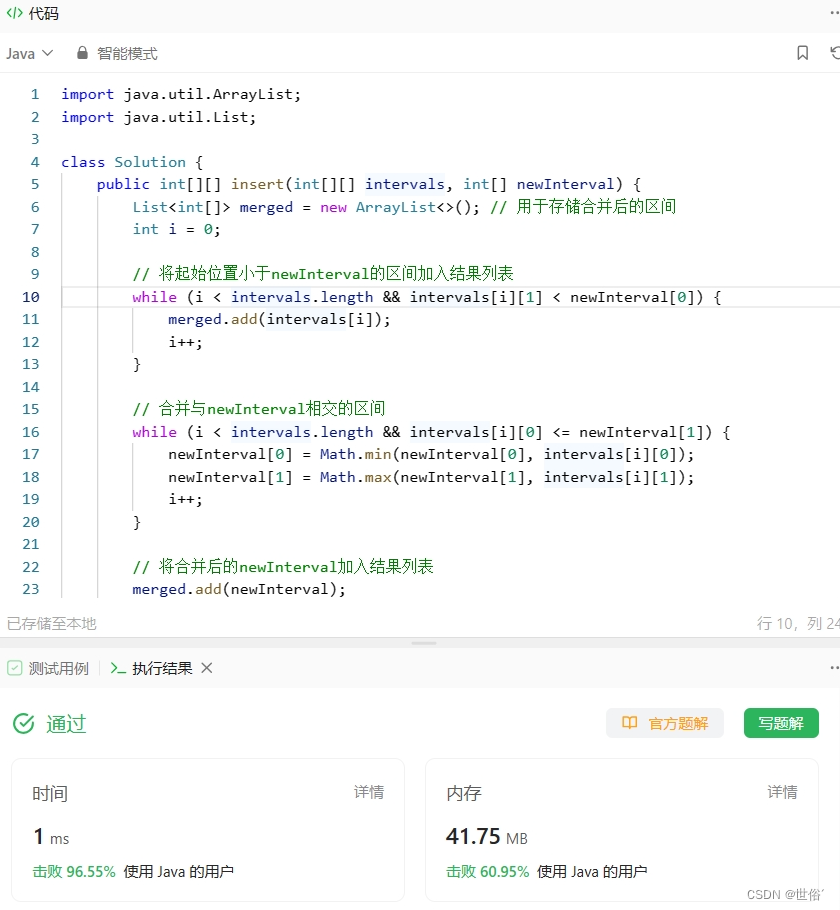
怒刷LeetCode的第23天（Java版）

目录 第一题 题目来源 题目内容 解决方法 方法一&#xff1a;贪心算法 方法二&#xff1a;动态规划 方法三&#xff1a;回溯算法 方法四&#xff1a;并查集 第二题 题目来源 题目内容 解决方法 方法一&#xff1a;排序和遍历 方法二&#xff1a;扫描线算法 方法…...

编程日记 2023/10/4 13:52:53

Golang 中的调试技巧

掌握有效的策略和工具&#xff0c;实现顺畅的开发 调试是每位开发人员都必须掌握的关键技能。它是识别、隔离和解决代码库中问题的过程。在 Golang 的世界中&#xff0c;掌握有效的调试技巧可以显著提升您的开发工作流程&#xff0c;并帮助您创建更可靠和健壮的应用程序。在本…...

编程日记 2023/10/4 13:50:51

linux 监控内存利用率

监控内存利用率 使用free来分析CPU使用信息 #!/bin/bashDATE$(date %F" "%H:%M)IP$(ifconfig eth0 |awk -F [ :] /inet addr/{print $4}) MAIL"examplemail.com"TOTAL$(free -m |awk /Mem/{print $2})USE$(free -m |awk /Mem/{print $3-$6-$7})FREE$(($TO…...

编程日记 2023/10/4 13:49:50

43 验证二叉搜索树

验证二叉搜索树 理解题意&#xff1a;验证搜索二叉树&#xff1a;中序遍历是升序题解1 递归&#xff08;学习学习&#xff01;&#xff09;题解2 中序遍历&#xff08;保持升序&#xff09; 给你一个二叉树的根节点 root &#xff0c;判断其是否是一个 有效的二叉搜索树。 有…...

编程日记 2023/10/4 13:47:48

深度学习笔记之微积分及绘图

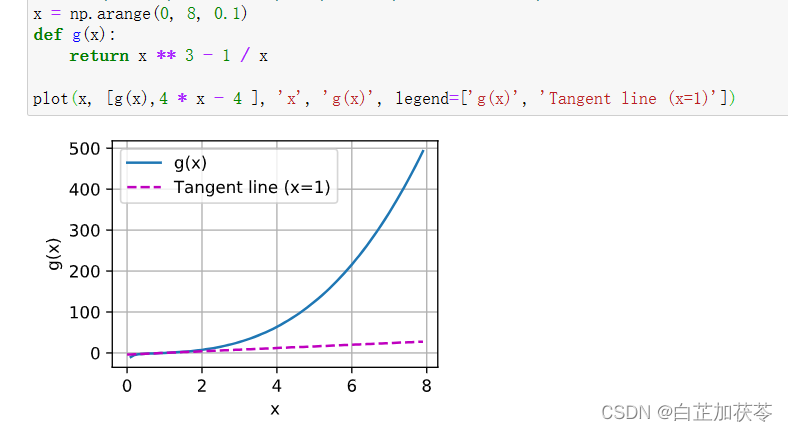
深度学习笔记之微积分及绘图 学习资料来源&#xff1a;微积分 %matplotlib inline from matplotlib_inline import backend_inline from mxnet import np, npx from d2l import mxnet as d2lnpx.set_np()def f(x):return 3 * x ** 2 - 4 * xdef numerical_lim(f, x, h):retur…...

编程日记 2023/10/4 13:43:44

java Spring Boot按日期 限制大小分文件记录日志

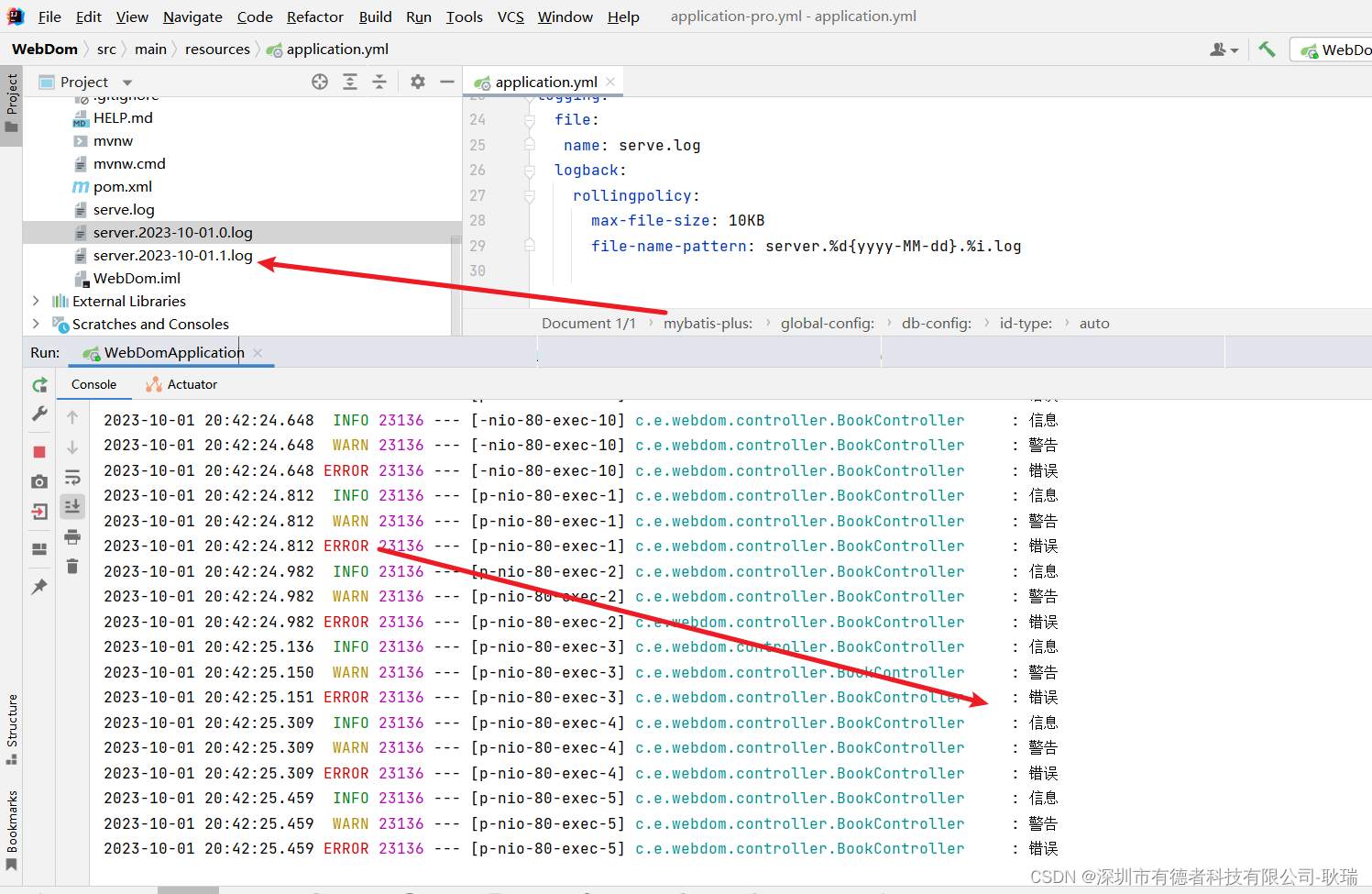
上文 java Spring Boot 将日志写入文件中记录 中 我们实现另一个将控制台日志写入到 项目本地文件的效果 但是 这里有个问题 比如 我项目是个大体量的企业项目 每天会有一百万用户访问 那我每天的日志都记载同一个文件上 那不跟没记没什么区别吗&#xff1f; 东西怎么找&#x…...

编程日记 2023/10/4 13:42:42

CSS 语法

CSS 实例 CSS 规则由两个主要的部分构成&#xff1a;选择器&#xff0c;以及一条或多条声明: 选择器通常是您需要改变样式的 HTML 元素。 每条声明由一个属性和一个值组成。 属性&#xff08;property&#xff09;是您希望设置的样式属性&#xff08;style attribute&#x…...

编程日记 2023/10/4 13:41:41

P3 QT项目----记事本（3.8）

3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

编程新知 2026/2/1 6:56:36

第一篇：Agent2Agent (A2A) 协议——协作式人工智能的黎明

AI 领域的快速发展正在催生一个新时代&#xff0c;智能代理&#xff08;agents&#xff09;不再是孤立的个体&#xff0c;而是能够像一个数字团队一样协作。然而&#xff0c;当前 AI 生态系统的碎片化阻碍了这一愿景的实现&#xff0c;导致了“AI 巴别塔问题”——不同代理之间…...

编程新知 2026/1/31 3:30:33

BCS 2025｜百度副总裁陈洋：智能体在安全领域的应用实践

6月5日&#xff0c;2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席&#xff0c;并作《智能体在安全领域的应用实践》主题演讲&#xff0c;分享了在智能体在安全领域的突破性实践。他指出&#xff0c;百度通过将安全能力…...

编程新知 2026/2/1 11:33:19

【C语言练习】080. 使用C语言实现简单的数据库操作

080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码：使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出：5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

编程新知 2025/9/22 21:37:01

React---day11

14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store&#xff1a; 我们在使用异步的时候理应是要使用中间件的&#xff0c;但是configureStore 已经自动集成了 redux-thunk&#xff0c;注意action里面要返回函数 import { configureS…...

编程新知 2026/1/19 2:13:24

从“安全密码”到测试体系：Gitee Test 赋能关键领域软件质量保障

关键领域软件测试的"安全密码"&#xff1a;Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天&#xff0c;软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力&#xff0c;从金融交易到交通管控&#xff0c;这些关乎国计民生的关键领域…...

编程新知 2026/2/2 20:26:17

Axure 下拉框联动

实现选省、选完省之后选对应省份下的市区...

编程新知 2026/1/20 13:43:41

【FTP】ftp文件传输会丢包吗？批量几百个文件传输，有一些文件没有传输完整，如何解决？

FTP&#xff08;File Transfer Protocol&#xff09;本身是一个基于 TCP 的协议&#xff0c;理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况&#xff0c;主要原因包括&#xff1a; ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...

编程新知 2025/8/17 3:31:21

Pydantic + Function Calling的结合

1、Pydantic Pydantic 是一个 Python 库&#xff0c;用于数据验证和设置管理&#xff0c;通过 Python 类型注解强制执行数据类型。它广泛用于 API 开发&#xff08;如 FastAPI&#xff09;、配置管理和数据解析&#xff0c;核心功能包括&#xff1a; 数据验证&#xff1a;通过…...

编程新知 2025/9/12 8:55:56

命令行关闭Windows防火墙

命令行关闭Windows防火墙 引言一、防火墙：被低估的"智能安检员"二、优先尝试！90%问题无需关闭防火墙方案1：程序白名单（解决软件误拦截）方案2：开放特定端口（解决网游/开发端口不通）三、命令行极速关闭方案方法一：PowerShell（推荐Win10/11）​方法二：CMD命令…...

编程新知 2025/8/27 20:07:03