2024级199管理类联考之数学基础(下篇)
平面几何(平均2题)
三角形(性质、特殊三角形、全等与相似)
- 性质
- 由不在同一直线的三条线段首尾依次连接所组成的图形
- 三条边、三个内角、三个定点
- 三角形内角和为180度,外角和为360度,多边形的外角和为360度,n多边形的内角和为(n-2)*180度
- 一个外角等于不相邻的两个内角之和
- 任意两边之和大于第三边,任意两边之差小于第三边,即大角对大边,等角对等边
- 三角形的两边中点的连线平行于第三边,且等于第三边边长的一半
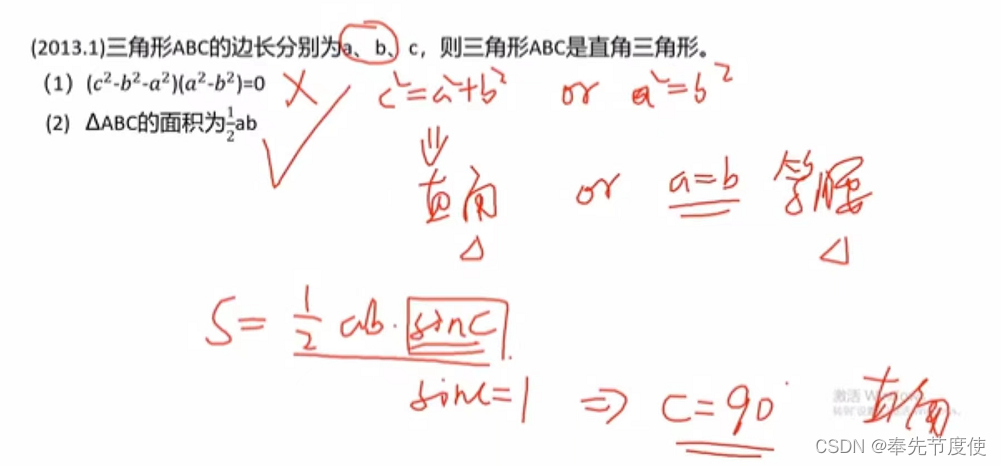
- 三角形面积S=1/2ah=1/2absinC
- 当已知条件仅说明三条边的长度,那就需要使用海伦公式S=根号下p(p-a)(p-b)(p-c),其中p=1/2(a+b+c)
- 三角形四心
- 内心:三角形内角平分线的交点(即三角形内切圆的圆心,到三角形三边的距离相等)
- 外心:三条边的垂直平分线的交点(三角形外接圆的圆心,到三个顶点距离相等)
- 重心:三条中线的交点
- 垂心:三条高线的交点
- 等边三角形四心合一,等腰三角形底边四线合一
- 三角形面积考点
- 两个三角形
- 同底等高,则面积相等
- 同底不等高,面积比等于高之比
- 等高不同底,面积比等于底之比
- 蝶形定理(针对梯形)
- 梯形ABCD中,下底与上底之比为k,即CD:AB=k:1
- 若蝴蝶头部Sabe=S,则蝴蝶腰部Sade=Sbec=kS,蝴蝶尾部Sdec=K^2S
- 即蝴蝶腰部*蝴蝶腰部=蝴蝶头部*蝴蝶尾部(即三部分面积成等比数列)
- 梯形ABCD中,下底与上底之比为k,即CD:AB=k:1
- 两个三角形
- 三角形分类
- 直角三角形
- 勾股定理(等价于外国称为毕达哥拉斯):a^2+b^2=c^2(a^2+b^2>c^2表示锐角三角形,反之为钝角三角形)
- 射影定理
- 斜边上的高是两直角边在斜边上射影的比例中项,即高^2=射影1*射影2
- 每一条直角边是这条直角边在斜边上的射影和斜边的比例中项(直角边^2=斜边*射影)
- 等腰直角三角形
- 边长关系比为1:1:根号下2
- 面积公式S=1/2a^2=1/4c^2,a为直角边,c为斜边
- 锐角为30度的直角三角形30度对边的边长为斜边一半,三边关系为1:根号下3:2
- 等腰三角形
- 四线合一: 底边高、中线、垂直平分线、顶角角平分线
- 120度的等腰三角形,三边比例为1:1:根号下3,如果腰长为a,则面积S=根号下3/4 *a^2
- 等边三角形
- 四心合一
- 面积S=根号下3/4 *a^2
- 直角三角形
- 三角形全等、相似
- 全等:两个全等三角形的对应边相等、对应角相等
- 判定全等的充分条件
- 两个三角形有两条边及其夹角对应相等(SAS)
- 两个三角形有2个角及其夹边对应相等(ASA)
- 两个三角形3条边对应相等(SSS)
- 判定全等的充分条件
- 相似
- 性质:两个相似三角形面积比=相似比平方
- 判定充分条件
- 两个三角形有一个内角对应相等,其两条夹边对应成比例
- 两个三角形有2个内角对应相等
- 两个三角形的3条边对应成比例
- 全等:两个全等三角形的对应边相等、对应角相等

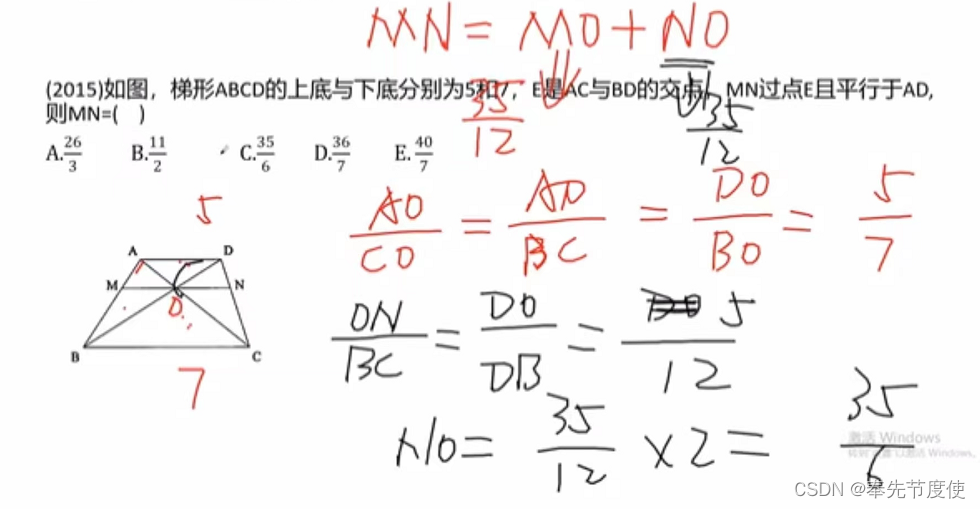


四边形(平行四边形、矩形、正方形、菱形、梯形)
- 平行四边形性质
- 平行四边形对边相等,对角相等,对角线互相平分
- 一对对边平行且相等的四边形
- S平行四边形=ah(底*高),周长C=2(a+b)
- 菱形性质
- 有一组邻边相等的平行四边形
- 四边相等的四边形一定是四边相等的平行四边形,即菱形
- 菱形的对角线互相垂直且平分顶角
- S菱形=1/2L1*L2(L1、L2为两对角线的长)
- 矩形性质
- 两对角线相等且互相平分
- S矩形=长*宽
- 正方形性质
- 正方形的对角线互相垂直且平分顶角
- S=a^2
- 梯形性质
- 一对对边平行
- 梯形两腰中点连线称为梯形的中位线且=1/2(上底+下底)
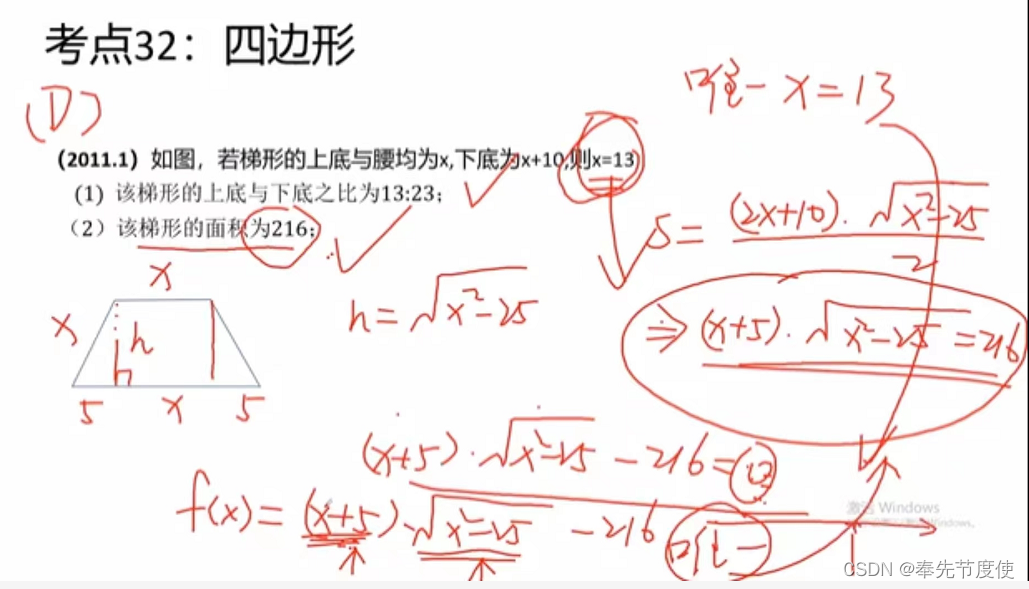
- S梯形=1/2(上底+下底)*高
- 等腰梯形性质
- 两条腰相等或者两个底角相等
- 两条对角线相等
- 若两对角线相互垂直,则高与中位线长度相等
圆
- 定义/性质
- 平面上与定点o距离等于定长r的动点轨迹称为圆,点o为圆心,r为半径
- S圆=πr^2,C圆=2πr
- 连接圆上任意两点的线段叫做弦,经过圆心的弦叫做直径
- 圆上任意两点间的部分叫做圆弧,大于半圆叫做优弧,小于半圆叫做劣弧
- 定点在圆上的角,它的两边分别与圆还有另外一个交点称为圆周角
- 一条弧所对的圆周角是它所对圆心角的一半
- 直径所对的圆周角为90度,90度圆周角所对的弦是直径
- 圆内两条圆弧相等,圆弧所对应的两组圆心角相等,两组圆周角也相等,即等弧对等角
- 圆的切线与圆的半径在切点出垂直
- 从圆外一点作圆的切线,两条切线相等
- 垂直定理
- 垂直于弦的直径平分弦且平分弦所对应的圆弧
扇形
- 角的弧度
- 360度=2π,180度=π...
- 扇形面积=n/360度*πr^2(n为扇形对应的圆心角角度,r为扇形半径)
- 弓形面积=S扇形-S三角形



立体几何(平均1题)
长方体
- 性质
- 6个面,12条棱,8个角
- V体积=abc,S面积=2(ab+ac+bc),体对角线d=根号下a^2+b^2+c^2
正方体
- 性质
- S面积=棱长*棱长*6=6a^2,V体积=a^3
- 体对角线=根号下3*a同时也是正方体中最长的线段
圆柱体
- 性质
- V体积=底面积*高=πr^2*h
- S侧面积=2πrh,S全面积=侧面积+底面积=2πrh+2πr^2
- L对角线=根号下(h^2+(2r)^2)
球体
- 性质
- R为球上一点到球心的距离,直径d=2R
- V体积=4/3πR^3
- S表面积=4πR^2

解析几何(平均2题)
平面直角坐标系
- 重点掌握两点间距离公式以及中点公式

平面直线
- 直线的倾斜角与斜率
- 倾斜角:直线与x轴正方向的夹角a,0<=a<=180度
- 斜率k:反映直线的倾斜程度,记为k=tana=(y2-y1)/(x2-x1)(a!=90度)
- 常见的两者对应关系
- tan0=0;tan180=0;tan45=1;tan135=-1;tan60=根号下3;tan120=-根号下3
- 直线方程常见形式
- 直线的点斜式:y-y0=k(x-x0),表示斜率为k且过点(x0,y0)的一条直线
- 直线的斜截式:y=kx+b表示斜率为k且与y轴相交于点(0,b)的直线,其中称b为直线的纵截距
- 直线一般方程:ax+by+c=0(a与b不全为0)
- 若a=0,方程为水平直线y= -c/b
- 若b=0,方程为竖直直线x= -c/a
- 若c=0,直线过原点(0,0)
- 若b!=0,则方程可写为y=-a/bx-c/b,直线斜率k=-a/b,纵截距y=-c/b,横截距x=-c/a
- 两直线位置关系
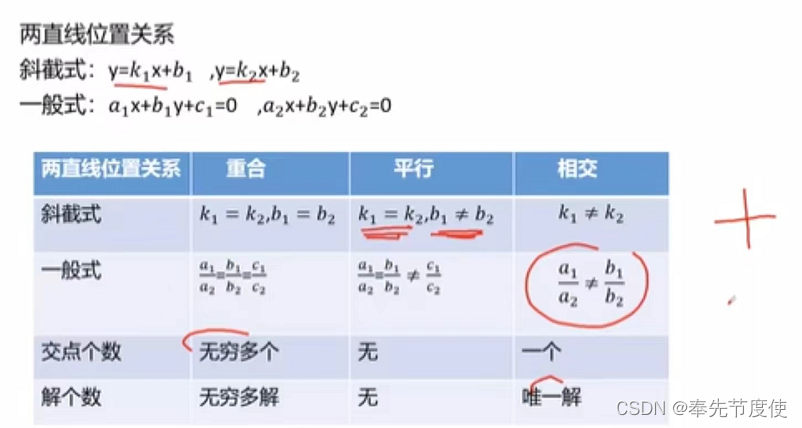

- 点到直线的距离公式

- 常用的对称关系

圆(直线与圆、圆与圆关系)
- 圆的方程
- 标准方程:以O(a,b)为圆心,r为半径的圆的方程为(x-a)^2+(y-b)^2=r^2
- 一般方程:x^2+y^2+Dx+Ey+F=0《=》(x+D/2)^2+(y+E/2)^2=D^2+E^2-4F/4;
- 可以得到圆心坐标O(-D/2,-E/2),半径r=根号下(D^2+E^2-4F)/2
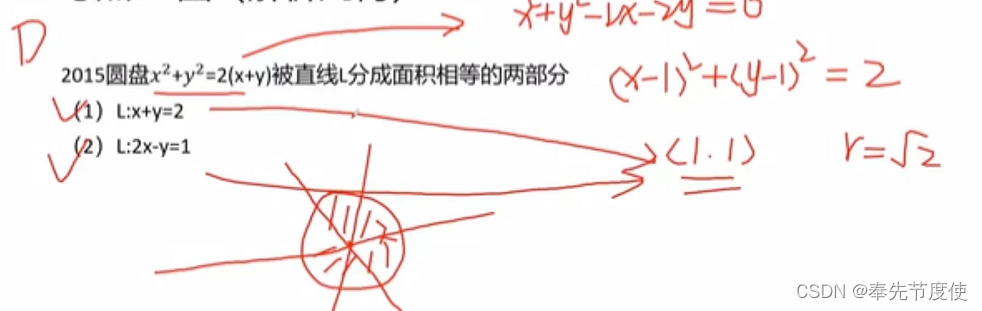
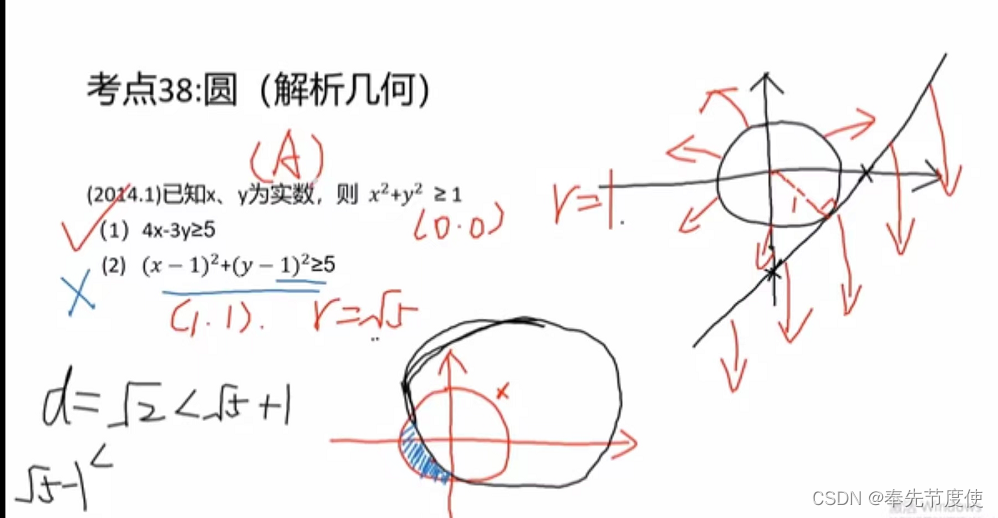
- 直线与圆的关系

- 圆与圆的关系


排列组合(平均1题)
加法与乘法原理
- 分类计数原理(加法原理):完成一件事,有n类办法,每类有多种方法,那么完成这件事的方法=每一类拥有的方法进行相加求和
- 分步计数原理(乘法原理):完成一件事,需要分成n个步骤,每步有多种方法,那么完成这件事的方法=每一步拥有的方法进行相乘求积
- 核心区别:能独立直接完成的属于分类计数(加法原理),不能直接完成需要分步完成的属于分步计数(乘法原理)
组合与组合数

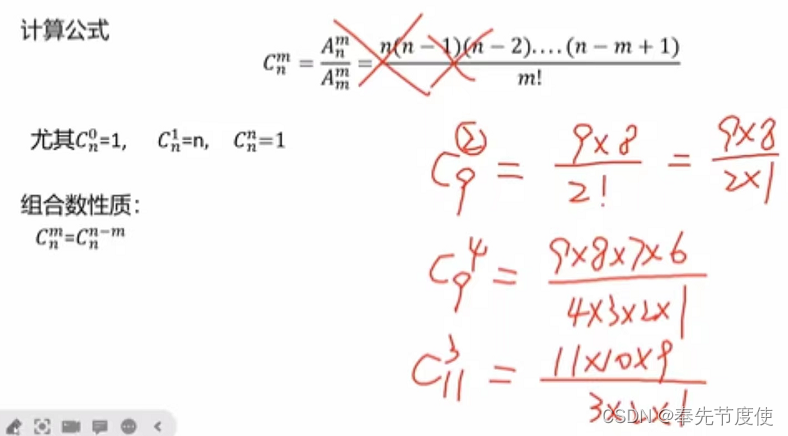
排列与排列数



排列组合步骤
-
先取后排:先选取出元素,然后再进行排列元素,不要边取边排(容易做错)
-
依次进行:按照一定的先后顺序排列
-
事情完成:整个事情必须完成
排列组合秒杀思路
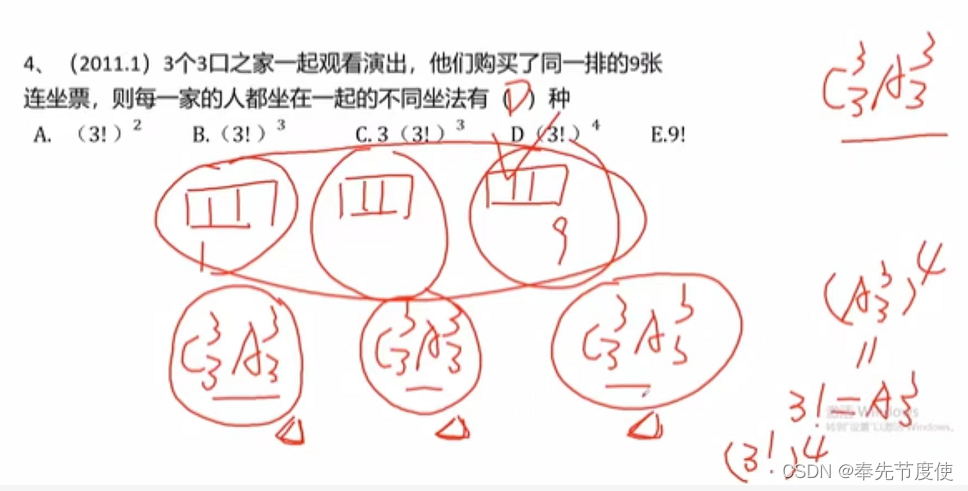
- 相邻问题/打包捆绑法
- 该方法主要解决若干个元素相邻问题
- 考题常见自然语言描述:紧挨着、相邻、一起...
- 解题思路:优先解决特殊要求的元素,并捆绑打包成一个整体
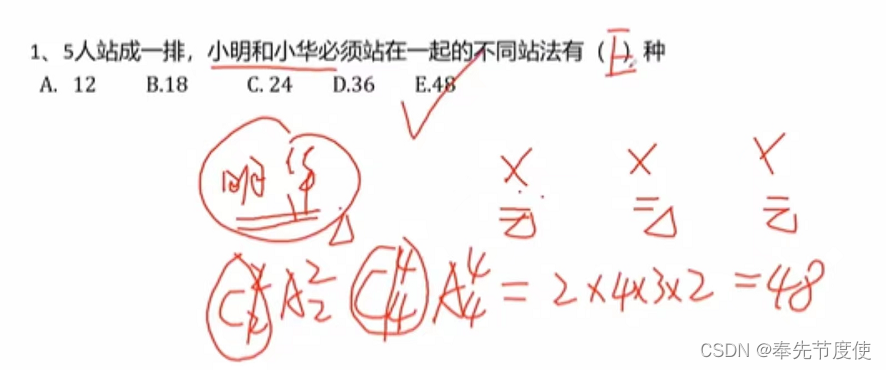
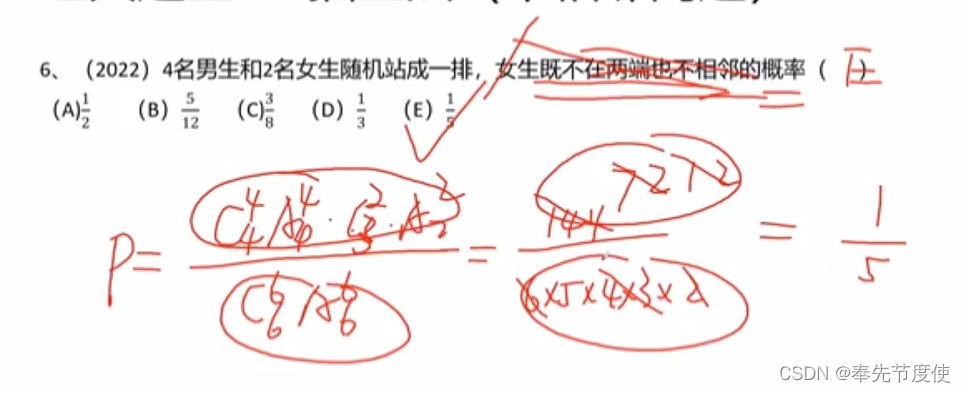
- 不相邻方法/插空法
- 该方法主要解决若干个元素不相邻问题
- 考题常见自然语言描述:不挨着、不相邻、不能连续...
- 解题思路:优先安排无任何要求的元素,再把特殊元素放入空位

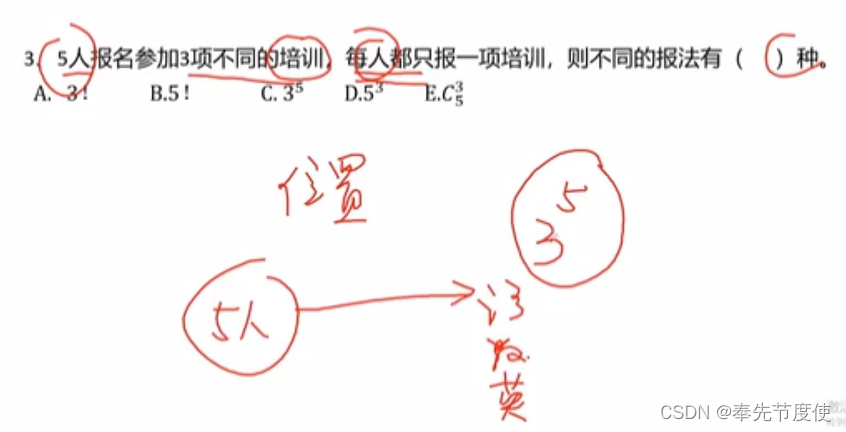
- 分房法(高频考点)
- 不同元素分配给不同的对象,对于分配对象分配的元素个数无限制
- 考题常见自然语言描述
- n个人去往m个不同的房间
- 个球放入m个不同的盒子
- n封信放入m个不同的信箱
- 解题思路:n个不同元素(指数位置)分配给m个位置(底数位置)对象,有m^n种方法
- 技巧:题目中只要出现"每”字,则紧跟着它的就是元素,即位于指数位置
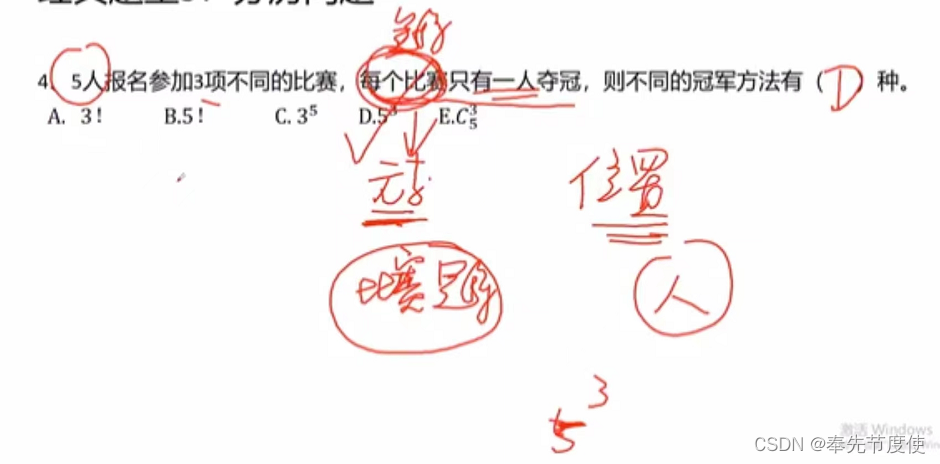
- 隔板法
- 相同元素分配给不同的对象,每个对象至少分到1个
- 考题常见自然语言描述
- n颗相同糖果分给m个小朋友,每人至少一个
- n个相同的球分给m个不同的盒子,每个盒子至少分一个小球
- n张相同的奖状分给m个不同的班级,每个班级至少一张奖状
- 解题思路:n个相同元素分配给m个不同对象,有C(m-1)(n-1)种方法


- 对号不对号
- 不对号问题
- 2个不对号,有1种方法
- 3个不对号,有2种方法
- 4个不对号,有9种方法
- 5个不对号,有44种方法
- 不对号问题


- 特殊元素问题
- 一个元素具备两个属性或多个属性,选取时要注意全能元素的归属
- 考题常见自然语言描述
- 某人既会英语又会法语
- 某人既会唱歌又会跳舞
- 解题思路:对全能元素进行分类讨论,含与不含全能元素的分类


- 局部元素定序法
- 当把n个元素进行排序的时候,其中若有m个元素是按照一定顺序已经定序
- 考题常见自然语言描述
- 甲乙丙从高到低
- 甲乙丙3人按照年龄大小
- 解题思路:此时就要把其中m个元素的顺序去掉,有多少就除以多少,定序公式=Ann/Amm


- 局部元素相同法
- 当对n个元素进行排序时,出现m个元素是完全相同的情况
- 考题常见自然语言描述
- 几个字母排序时出现3个A
- 挂旗时出现相同颜色的旗帜,如3面红旗
- 解题思路:根据所有元素数量的阶乘,除以相同元素数量的阶乘,有多少除以多少,定序公式=Ann/Amm


- 分堆与分配问题(高频考点)
- 若分堆出现相同数量的堆数,则要除以相同堆数的阶乘,以消除排序,若题目要求对元素进行分配,则一定先分堆再分配





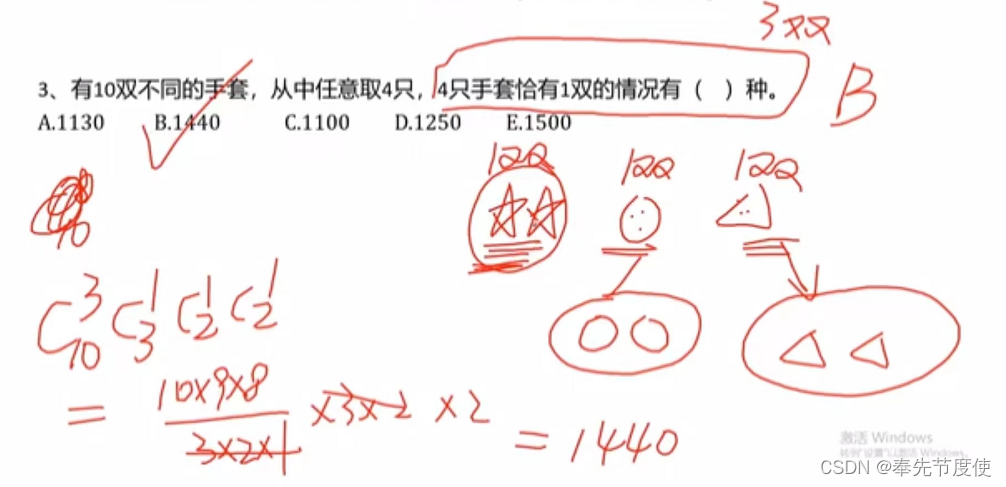
- 成双问题/配对问题
- 主要是以手套、袜子或鞋子等成双的物品作为对象,核心在于选取物品是否成双
- 成双问题:直接选取成双即可
- 不成双问题:先取双,再在双中取单只
- 主要是以手套、袜子或鞋子等成双的物品作为对象,核心在于选取物品是否成双



概率(平均1题)
随机事件相关概念
- 随机试验
- 实验可在相同的条件下重复进行
- 可能结果不止一个,且所有可能结果已知
- 每次实验出现的哪个结果是未知的
- 如:掷骰子,观察出现的点数
- 不可能事件概率是0,必然事件概率是1,随机事件概率(0,1)
- 事件A与事件B同时发生的事件为A与B的积事件即AB
- 事件A与事件B至少有一个发生的事件为A与B的和事件即A+B
概率定义与分类
- 事件A的概率是指随机事件A发生可能性大小的度量值记作P(A)
古典概型定义与分类
- 满足古典概型的条件
- 所有基本事件是有限个数
- 各基本事件发生的可能性相同
- 古典概型之摸球问题/取样问题



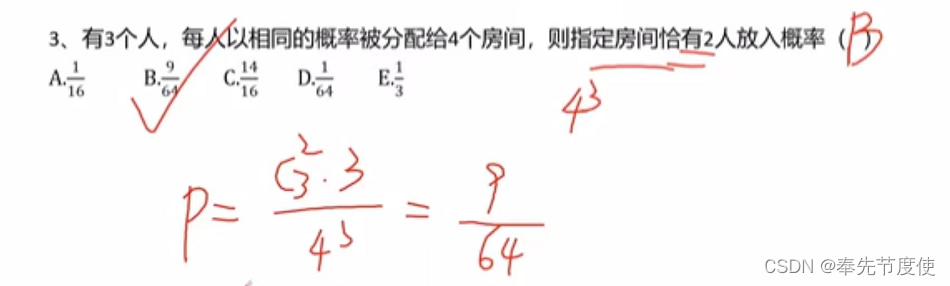
- 古典概型之分房问题



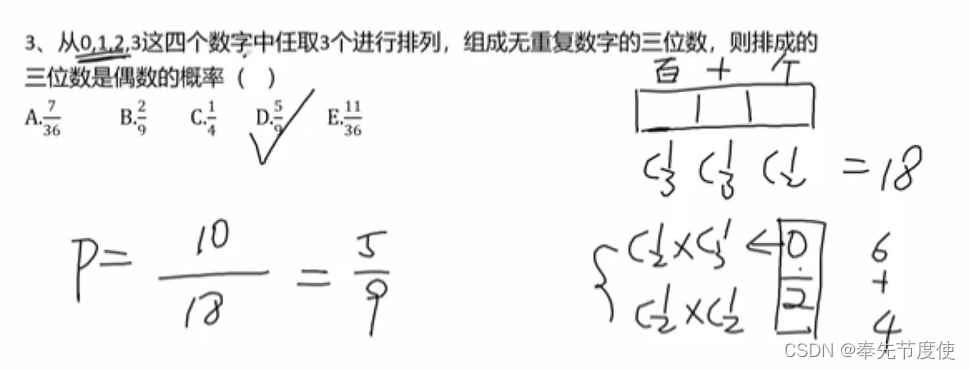
- 古典概型之数字问题


独立事件




独立重复试验/贝努力公式


数据描述(平均1题)
均值与方差









应用题(平均5题)
比例问题
- 按比例分配:把一个数按照一定比分成若干份
- 百分数问题:表示一个数是另一个数的百分之几的数
利润问题
- 利润=售价-进价(成本)
- 利润率=利润/进价=(售价-进价)/进价
- 售价=进价*(1+利润率)【即售价是进价的(1+利润率)倍,盈亏对应利润率的正负】
工程问题
- 主要分析工作量、工作效率和工作时间三者之间关系
- 工作量=工作时间*工作效率(工作量未说明时当做1)
- 工作时间=工作量/(甲工作效率+乙工作效率+xxx工作效率...)
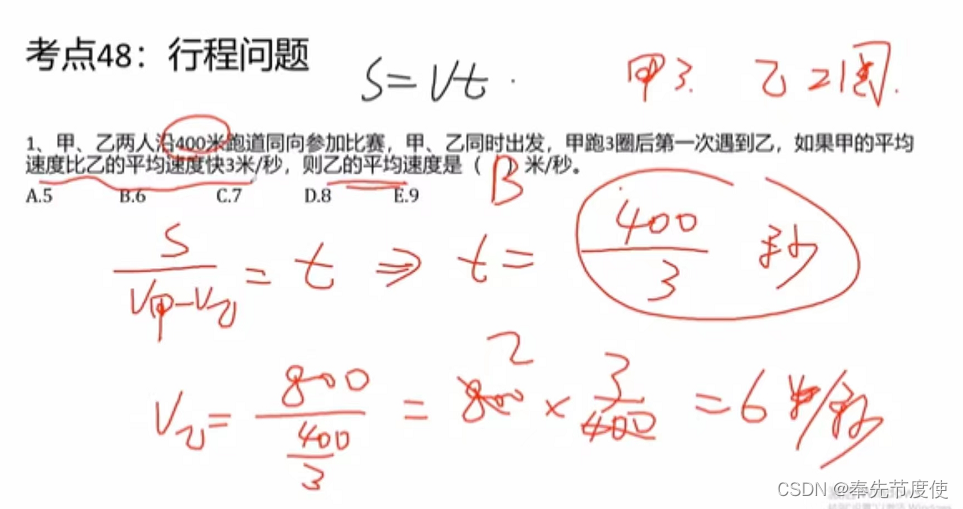
行程问题
相遇问题
- 两个运动物体同时由两地出发相向而行在途中相遇
- 解题思路为根据如下公式找等量关系,优先设速度
- 相遇时间=总路程/速度(如v甲+v乙)
- 总路程=速度和(如v甲+v乙) * 相遇时间
追击问题(环形追击时,每追上一次则多跑一圈)
- 两个运动物体作同向运动,在一定时间内后面物体追上前面物体
- 解题思路为根据如下公式找等量关系
- 追击时间=追击路程/速度(快速-慢速)
- 追击路程=速度(快速-慢速)*追击时间
列车问题
- 列车行驶运动要考虑列车车身长度
- 解题思路为根据如下公式找等量关系
- 火车过桥:过桥时间=(车长+桥长) / 车速
- 火车追击:追击时间=(甲车长+乙车长+距离) /(甲车速-乙车速)
- 火车相遇:相遇时间=(甲车长+乙车长+距离) /(甲车速+乙车速)
行船问题
- 船只航行问题,需要注意船速和水速,顺水航行时速度为船速和水速之和,逆水航行时速度为船速与水速之差
- 解题思路为根据如下公式找等量关系
- V顺水 = V船 + V水
- V逆水 = V船 - V水
- (V顺水 + V逆水) / 2 = 船速
- (V顺水 - V逆水) / 2 = 水速
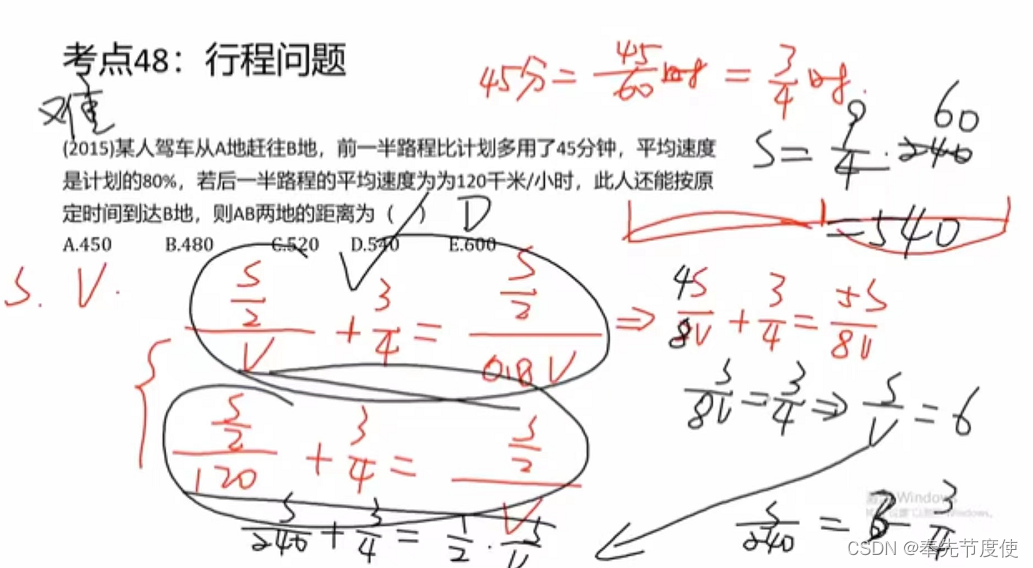
浓度问题
- 溶剂、溶质、溶液以及浓度的关系
- 根据如下公式找等量关系
- 溶液=溶剂+溶质(核心溶质不会变)
- 浓度=溶质/溶液*100%(核心溶质不会变)

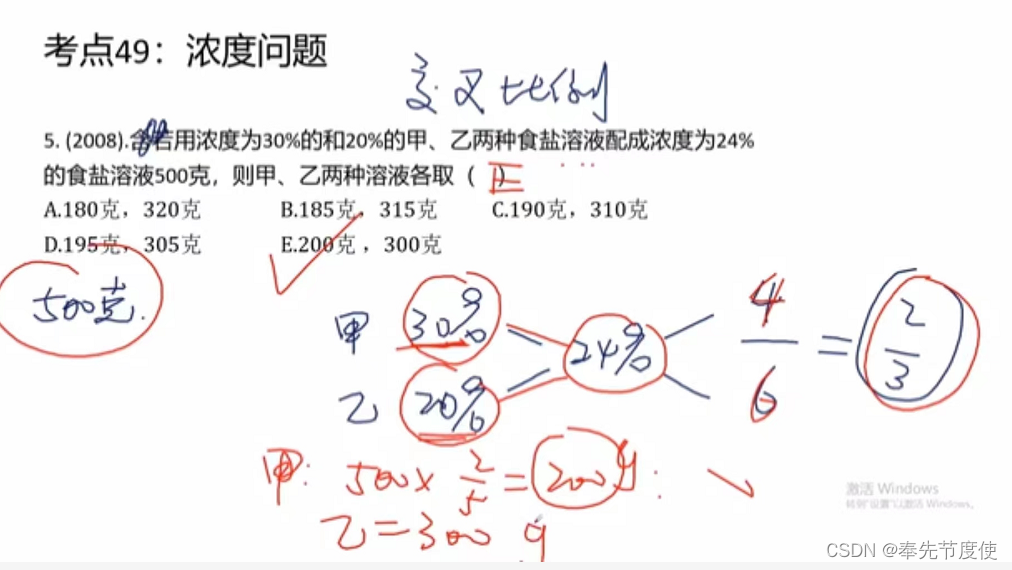
最值问题
- 实际生活中,经常追求以最小的代价取得最大的效果或效益,即最值问题
- 表现形式就是根据方程求最大值或最小值
- 二次函数方f(x)=ax2 + bx + c模型,利用开口和对称轴(x=-b/2a)求最值
- a>0开口向上,有最小值,反之开口向下有最大值
- 若知道二次函数根,则直接取两根中点处为最值
- 均值不等式模型,利用均值不等式求最值
- x2+y2>=2xy
- x + y >=2根号下xy
- 当且仅当x=y时等号成立
- 一正(x>0,y>0),二定(即x+y或xy为定值),三相等(x=y才会取到最值)
- 二次函数方f(x)=ax2 + bx + c模型,利用开口和对称轴(x=-b/2a)求最值
相关文章:

2024级199管理类联考之数学基础(下篇)
平面几何(平均2题) 三角形(性质、特殊三角形、全等与相似) 性质 由不在同一直线的三条线段首尾依次连接所组成的图形三条边、三个内角、三个定点三角形内角和为180度,外角和为360度,多边形的外角和为360度,n多边形的内角和为(n-2)*180度一个外角等于不相邻的两个内角之和任意…...

HTML之如何下载网页中的音频(二)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生…...
【现代机器人学】学习笔记十四:中文版印刷/翻译勘误
首先声明,这个印刷/勘误并非经过官方的认可,只是我个人的粗浅的理解。如果内容有误,恳请大家谅解指正。 其实有的并不算错,只是我个人认为不太准确,在我学习过程中产生了一些小疑惑和误解。 都是一些小毛病ÿ…...
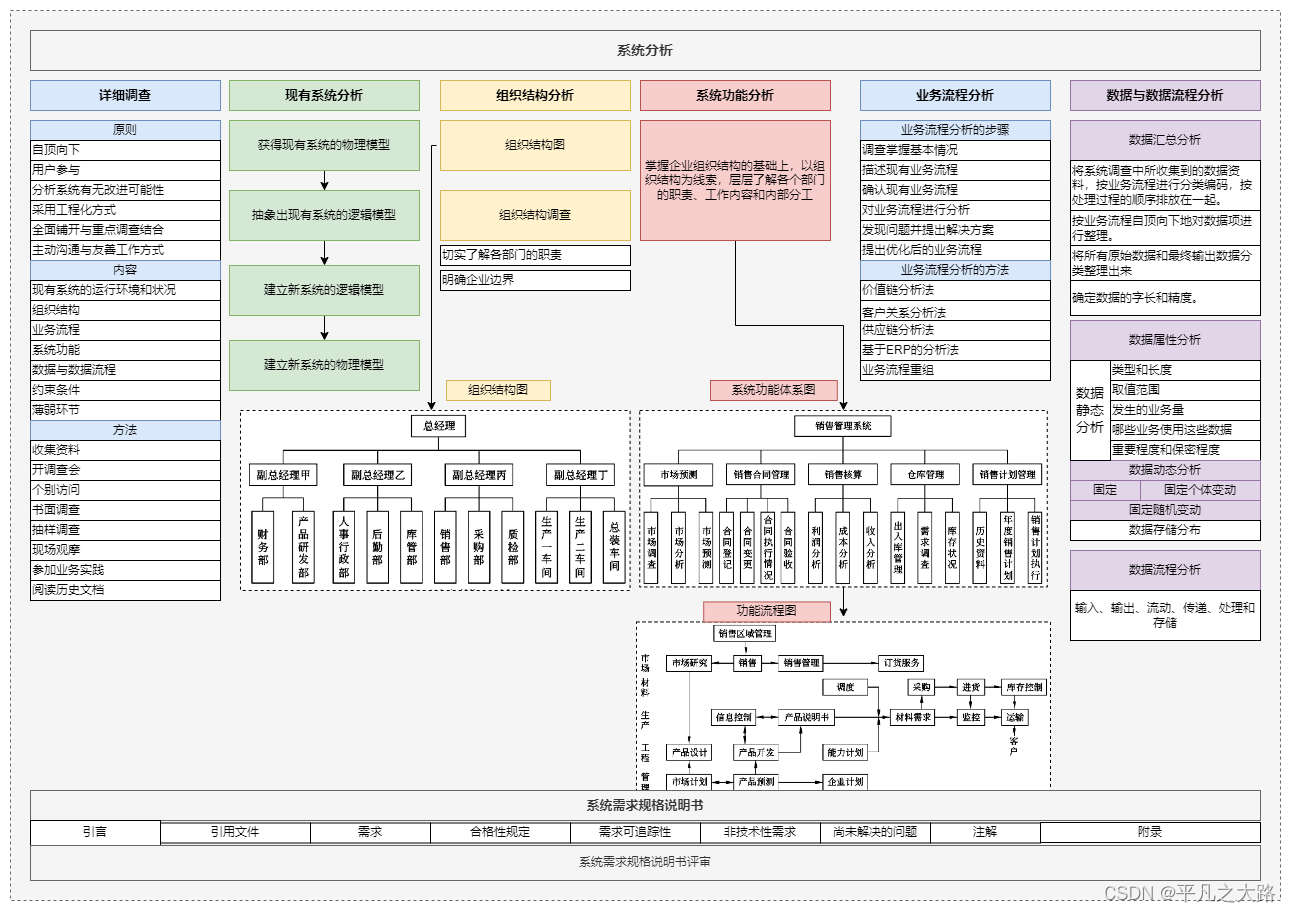
[架构之路-229]:计算机体硬件与系结构 - 计算机系统的矩阵知识体系结构
目录 一、纵向:目标系统的分层结构 1.1 目标系统的架构 1.2 网络协议栈 1.3 计算机程序语言分层 二、横向(构建目标系统的时间、开发阶段):软件工程 三、二维矩阵知识体系结构 一、纵向:目标系统的分层结构 1.1…...
第一章 visual studio下载安装
一、官网下载 地址:https://visualstudio.microsoft.com/zh-hans/ 点击免费visual studio 二、安装 运行下载好的exe文件,自定义安装目录 三、选择需要的组件安装 只需要选择标记组件,然后点击安装 等待安装完成就行 四、重启电脑 安装完之后…...

【服务器】在 Linux CLI 下安装 Anaconda
【服务器】在 Linux CLI 下安装 Anaconda 1 系统环境2 下载安装包3 安装 1 系统环境 查看系统信息 cat /etc/os-release2. 查看架构 uname -a # output # Linux localhost.localdomain 4.18.0-193.28.1.el8_2.x86_64 #1 SMP Thu Oct 22 00:20:22 UTC 2020 x86_64 x86_64 x86…...

Python中Lambda用法
在Python中,lambda函数是一种形式较短的函数,又称为匿名函数。与正常的函数不同,lambda函数没有名称,因此只能在定义时直接传递给其他函数或变量使用,而不能单独调用。 lambda函数的语法非常简单,格式如下…...
nodejs+vue养老人员活体鉴权服务系统elementui
系统 统计数据:统计报表、人员台账、机构数据、上报数据、核验报表等,养老人员活体鉴权服务是目前国家养老人员管理的重要环节,主要为以养老机构中养老人员信息为基础,每月进行活体鉴权识别并统计数据为养老补助等管理。前端功能&…...
)
解决caffe中的python环境安装的问题(补充)
上一篇(解决caffe中的python环境安装的问题_qiuchangyong的博客-CSDN博客)说到了安装过程中遇到的常见问题,其实还有一个忘了补充,就是在执行命令"sudo python -m pip install -r requirements.txt"后,出现p…...

面试常用排序查找算法
文章目录 1 二分查找2 冒泡排序3 堆排序4 插入排序5 快速排序6 选择排序7 希尔排序 1 二分查找 定义两个变量left和right,分别表示数组的左边界和右边界,初始值分别为0和len - 1,其中len是数组的长度。计算数组的中间位置mid,公式…...

CUDA C编程权威指南:1.1-CUDA基础知识点梳理
主要整理了N多年前(2013年)学习CUDA的时候开始总结的知识点,好长时间不写CUDA代码了,现在LLM推理需要重新学习CUDA编程,看来出来混迟早要还的。 1.CUDA 解析:2007年,NVIDIA推出CUDA(…...

讲讲项目里的仪表盘编辑器(四)分页卡和布局容器组件
讲讲两个经典布局组件的实现 ① 布局容器组件 配置面板是给用户配置布局容器背景颜色等属性。这里我们不需要关注 定义文件 规定了组件类的类型、标签、图标、默认布局属性、主文件等等。 // index.js import Container from ./container.vue; class ContainerControl extends…...

Qt模块、Qt开发应用程序类型、Qt未来主要市场、Qt6功能普及
Qt模块、Qt开发应用程序类型、Qt未来主要市场、Qt6功能普及 文章目录 1.Qt核心模块2.Qt的功能拓展3.Qt未来主要市场4.Qt6功能普及5.弃用的功能: Qt是一个跨平台的应用程序开发框架,提供了丰富的模块和工具来开发各种类型的应用程序。以下是Qt目前已有的…...

nodejs+vue高校校图书馆elementui
管理员输入书籍所在的书架位置,借阅提醒系统:可以查看个人借阅信息和图书到期提醒、挂失、检索、虚拟借书证不仅为群众提供了服务,而且也推广了自己,让更多的群众了解自己。 管理员页面: 第三章 系统分析 10 3.1需求分…...

CUDA C编程权威指南:1.2-CUDA基础知识点梳理
主要整理了N多年前(2013年)学习CUDA的时候开始总结的知识点,好长时间不写CUDA代码了,现在LLM推理需要重新学习CUDA编程,看来出来混迟早要还的。 1.闭扫描和开扫描 对于一个二元运算符 ⊕ \oplus ⊕和一个 n n n元…...

C语言—位运算符
目录 &(位与,AND): |(位或,OR): 位取反(~): 左移(<<): 右移(>>): &(位与,AND)&…...

怎么才能实现一个链接自动识别安卓.apk苹果.ipa手机和win电脑wac电脑
您想要实现的功能是通过检测用户代理(User Agent)来识别访问设备类型并根据设备类型展示相应的页面。您可以根据以下步骤进行实现: 选择后端语言和框架,例如:Node.js、Express。 创建一个新的Express项目。 编写一个…...
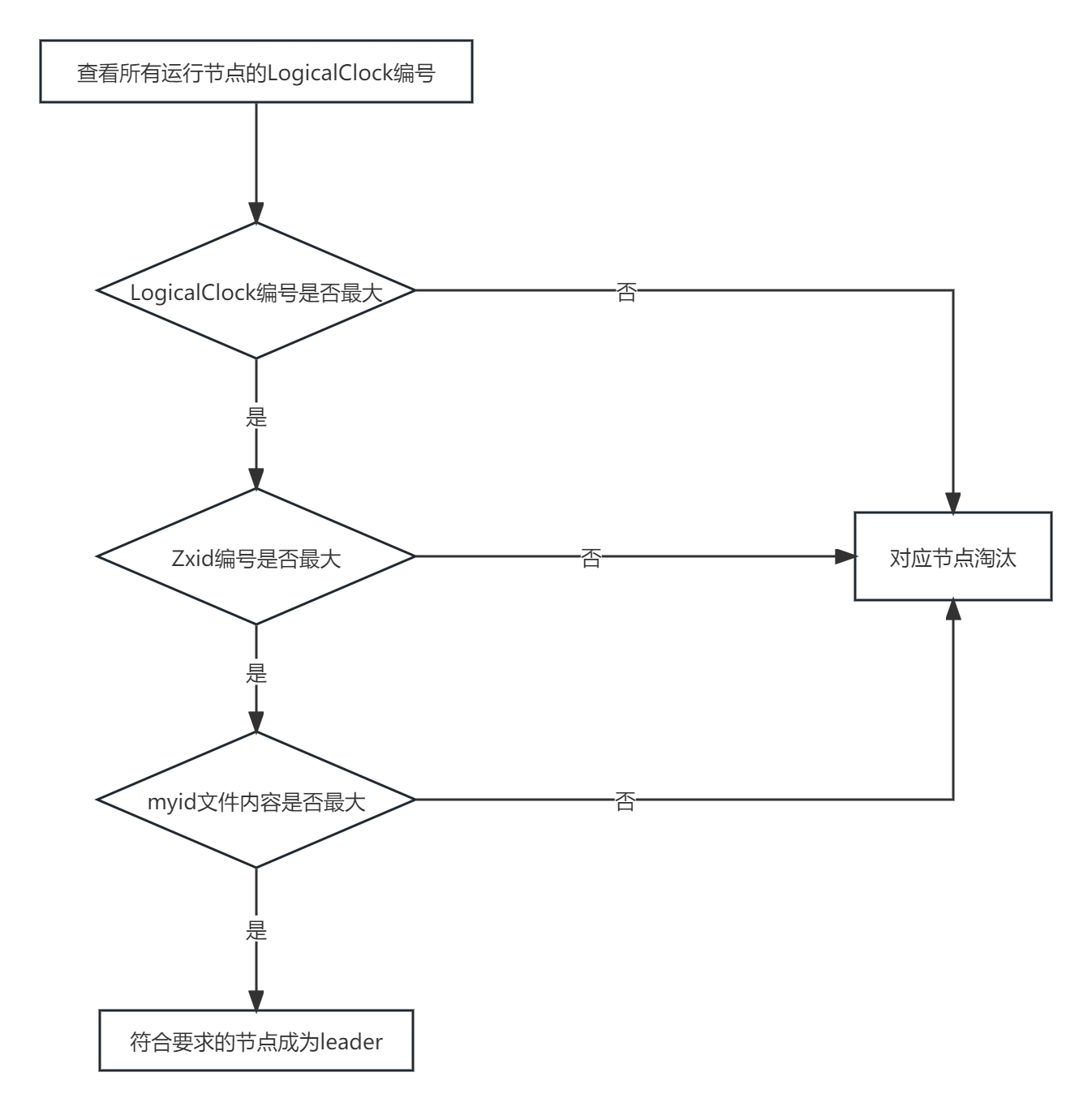
zookeeper选举机制
全新集群选举 zookeeper 全新集群选举机制网上资料很多说法很模糊,仔细思考了一下,应该是这样 得到票数最多的机器>机器总数半数 具体启动过程中的哪个节点成为 leader 与 zoo.cfg 中配置的节点数有关,下面以3个举例 选举过程如下 server…...

vcpkg切换 Visual Studio 版本
vcpkg切换 Visual Studio 版本 在使用vcpkg作为项目的包管理工具时,可能会遇到需要切换Visual Studio版本的情况。下面是一种简单的方法来实现这个目标,通过修改triplet文件来指定使用的Visual Studio版本。 步骤1: 创建或修改Triplet文件 首先&#…...
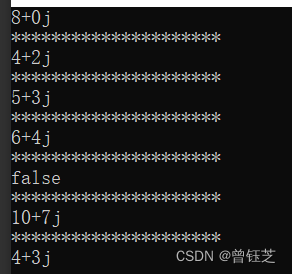
运算符重载
#include <iostream> using namespace std; class Num { private:int num1; //实部int num2; //虚部 public:Num(){}; //无参构造Num(int n1,int n2):num1(n1),num2(n2){}; //有参构造~Num(){}; //析构函数const Num operator(const Num &other)const //加号重载{Nu…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...
