十天学完基础数据结构-第九天(堆(Heap))

堆的基本概念
堆是一种特殊的树形数据结构,通常用于实现优先级队列。堆具有以下两个主要特点:
-
父节点的值始终大于或等于其子节点的值(最大堆),或者父节点的值始终小于或等于其子节点的值(最小堆)。
-
堆是一棵完全二叉树,这意味着所有层级除了最后一层都是完全填满的,最后一层从左到右填充。
最大堆和最小堆的定义
-
最大堆(Max Heap):在最大堆中,父节点的值始终大于或等于其子节点的值,这意味着根节点是堆中的最大元素。
-
最小堆(Min Heap):在最小堆中,父节点的值始终小于或等于其子节点的值,这意味着根节点是堆中的最小元素。
堆的常见操作
堆支持一些常见的操作,包括:
-
插入(Insertion):将新元素插入堆中,然后重新调整堆,以维护堆的性质。
-
删除(Deletion):删除堆中的根节点,然后重新调整堆,以维护堆的性质。
-
堆排序(Heap Sort):使用堆进行排序,将堆顶元素(最大或最小元素)与最后一个元素交换,然后减小堆的大小,并重新调整堆,重复此过程直到排序完成。
任务
堆在许多算法中都有广泛应用,包括Dijkstra算法、优先级队列等。掌握堆排序算法,这是一种高效的排序算法。
示例代码 - 使用C++创建最大堆和进行堆排序:
#include <iostream>
#include <vector>
#include <algorithm>class MaxHeap {
public:MaxHeap() {}// 插入元素void insert(int value) {heap.push_back(value);int index = heap.size() - 1;heapifyUp(index);}// 删除最大元素void removeMax() {if (isEmpty()) {return;}std::swap(heap[0], heap.back());heap.pop_back();heapifyDown(0);}// 堆排序void heapSort() {int n = heap.size();for (int i = n / 2 - 1; i >= 0; i--) {heapifyDown(i);}for (int i = n - 1; i > 0; i--) {std::swap(heap[0], heap[i]);heapifyDown(0, i);}}// 判断堆是否为空bool isEmpty() {return heap.empty();}private:std::vector<int> heap;void heapifyUp(int index) {while (index > 0) {int parent = (index - 1) / 2;if (heap[index] <= heap[parent]) {break;}std::swap(heap[index], heap[parent]);index = parent;}}void heapifyDown(int index, int size = -1) {if (size == -1) {size = heap.size();}while (true) {int leftChild = 2 * index + 1;int rightChild = 2 * index + 2;int largest = index;if (leftChild < size && heap[leftChild] > heap[largest]) {largest = leftChild;}if (rightChild < size && heap[rightChild] > heap[largest]) {largest = rightChild;}if (largest == index) {break;}std::swap(heap[index], heap[largest]);index = largest;}}
};int main() {MaxHeap maxHeap;maxHeap.insert(5);maxHeap.insert(10);maxHeap.insert(3);maxHeap.insert(8);maxHeap.insert(1);std::cout << "堆排序前:";for (int num : maxHeap) {std::cout << num << " ";}maxHeap.heapSort();std::cout << "\n堆排序后:";for (int num : maxHeap) {std::cout << num << " ";}return 0;
}
练习题:
-
解释堆的基本概念中的最大堆和最小堆的定义。
-
描述堆排序的步骤。
-
为什么堆可以用于高效的优先级队列实现?
-
在给定的一组元素中,如何创建一个最大堆?使用C++编写相应的代码。
-
在给定的一组元素中,如何使用堆排序进行排序?使用C++
解释堆的基本概念中的最大堆和最小堆的定义。
-
最大堆(Max Heap):在最大堆中,每个父节点的值都大于或等于其子节点的值。这意味着根节点包含堆中的最大元素。
-
最小堆(Min Heap):在最小堆中,每个父节点的值都小于或等于其子节点的值。这意味着根节点包含堆中的最小元素。
描述堆排序的步骤。
堆排序是一种原地、稳定的排序算法,它的步骤如下:
-
构建一个最大堆或最小堆,将数组视为堆。
-
不断从堆顶(最大值或最小值)移除元素,并将其放入已排序部分的末尾。
-
重复第二步,直到堆为空。
这个过程保证了每次移除的元素都是当前堆中的最大(最小)值,因此最终得到一个有序的数组。
为什么堆可以用于高效的优先级队列实现?
堆可以用于高效的优先级队列实现,因为堆的结构允许我们快速找到并删除最大(最小)元素,以及迅速插入新元素。这在许多算法和数据结构中都非常有用,如Dijkstra算法、Prim算法、任务调度等。堆的时间复杂度为O(log n),其中n是堆的大小,这使得优先级队列的操作非常高效。
在给定的一组元素中,如何创建一个最大堆?使用C++编写相应的代码。
创建最大堆的关键是从数组构建一个满足最大堆性质的堆。以下是使用C++创建最大堆的示例代码:
#include <iostream>
#include <vector>void maxHeapify(std::vector<int>& arr, int size, int i) {int largest = i;int left = 2 * i + 1;int right = 2 * i + 2;if (left < size && arr[left] > arr[largest]) {largest = left;}if (right < size && arr[right] > arr[largest]) {largest = right;}if (largest != i) {std::swap(arr[i], arr[largest]);maxHeapify(arr, size, largest);}
}void buildMaxHeap(std::vector<int>& arr) {int size = arr.size();for (int i = size / 2 - 1; i >= 0; i--) {maxHeapify(arr, size, i);}
}int main() {std::vector<int> arr = {4, 10, 3, 5, 1};int size = arr.size();buildMaxHeap(arr);std::cout << "最大堆:";for (int num : arr) {std::cout << num << " ";}return 0;
}
运行结果:
在给定的一组元素中,如何使用堆排序进行排序?使用C++编写相应的代码。
堆排序的关键是将堆顶元素与数组末尾元素交换,然后减小堆的大小并重新调整堆。以下是使用C++进行堆排序的示例代码:
#include <iostream>
#include <vector>void maxHeapify(std::vector<int>& arr, int size, int i) {int largest = i;int left = 2 * i + 1;int right = 2 * i + 2;if (left < size && arr[left] > arr[largest]) {largest = left;}if (right < size && arr[right] > arr[largest]) {largest = right;}if (largest != i) {std::swap(arr[i], arr[largest]);maxHeapify(arr, size, largest);}
}void heapSort(std::vector<int>& arr) {int size = arr.size();for (int i = size / 2 - 1; i >= 0; i--) {maxHeapify(arr, size, i);}for (int i = size - 1; i > 0; i--) {std::swap(arr[0], arr[i]);maxHeapify(arr, i, 0);}
}int main() {std::vector<int> arr = {4, 10, 3, 5, 1};int size = arr.size();heapSort(arr);std::cout << "堆排序结果:";for (int num : arr) {std::cout << num << " ";}return 0;
}
运行结果:
相关文章:

十天学完基础数据结构-第九天(堆(Heap))
堆的基本概念 堆是一种特殊的树形数据结构,通常用于实现优先级队列。堆具有以下两个主要特点: 父节点的值始终大于或等于其子节点的值(最大堆),或者父节点的值始终小于或等于其子节点的值(最小堆ÿ…...
vertx的学习总结7之用kotlin 与vertx搞一个简单的http
这里我就简单的聊几句,如何用vertx web来搞一个web项目的 1、首先先引入几个依赖,这里我就用maven了,这个是kotlinvertx web <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apac…...
:链路追踪)
golang学习笔记(二):链路追踪
自定义http连接的服务端 package serverimport ("github.com/gin-gonic/gin""go.opentelemetry.io/contrib/instrumentation/github.com/gin-gonic/gin/otelgin""net/http" )type MyServer struct {Server *http.Server }func GetServer() *MyS…...
git提交代码实际操作
1.仓库的代码 2.克隆代码下存在的分支 git clobe https://gitee.com/sadsadasad/big-event-11.git 3.查看当下存在的分支 git branch -a 在很多情况下,我们是要围绕着dev分支进行开发,所以我们可以在开发之前问明白围绕那个分支进行开发。 4.直接拉去dev分支代码 5.如果没在…...
TF坐标变换
ROS小乌龟跟随 5.1 TF坐标变换 Autolabor-ROS机器人入门课程《ROS理论与实践》零基础教程 tf模块:在 ROS 中用于实现不同坐标系之间的点或向量的转换。 在ROS中坐标变换最初对应的是tf,不过在 hydro 版本开始, tf 被弃用,迁移到 tf2,后者更…...

如何进行网络编程和套接字操作?
网络编程是计算机编程中重要的领域之一,它使程序能够在网络上进行数据传输和通信。C语言是一种强大的编程语言,也可以用于网络编程。网络编程通常涉及套接字(Socket)操作,套接字是一种用于网络通信的抽象接口。本文将详…...

在Spark中集成和使用Hudi
本文介绍了在Spark中集成和使用Hudi的功能。使用Spark数据源API(scala和python)和Spark SQL,插入、更新、删除和查询Hudi表的代码片段。 1.安装 Hudi适用于Spark-2.4.3+和Spark 3.x版本。 1.1 Spark 3支持矩阵 Hudi...
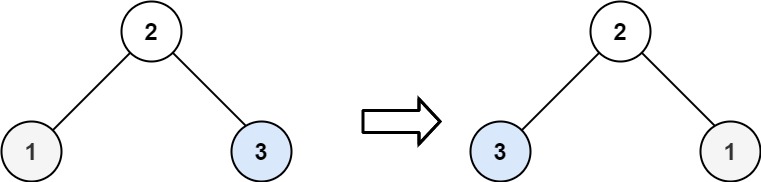
力扣第226翻转二叉数 c++三种方法 +注释
题目 226. 翻转二叉树 简单 给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。 示例 1: 输入:root [4,2,7,1,3,6,9] 输出:[4,7,2,9,6,3,1]示例 2: 输入:root [2,1,3] 输出&am…...
React项目部署 - Nginx配置
写在前面:博主是一只经过实战开发历练后投身培训事业的“小山猪”,昵称取自动画片《狮子王》中的“彭彭”,总是以乐观、积极的心态对待周边的事物。本人的技术路线从Java全栈工程师一路奔向大数据开发、数据挖掘领域,如今终有小成…...
【Vue3】定义全局变量和全局函数
// main.ts import { createApp } from vue import App from ./App.vue const app createApp(App)// 解决 ts 报错 type Filter {format<T>(str: T): string } declare module vue {export interface ComponentCustomProperties {$filters: Filter,$myArgs: string} }a…...

【Pandas】Apply自定义行数
文章目录 1. Series的apply方法2. DataFrame的apply方法2.1 针对列使用apply2.2 针对行使用apply Pandas提供了很多数据处理的API,但当提供的API不能满足需求的时候,需要自己编写数据处理函数, 这个时候可以使用apply函数apply函数可以接收一个自定义函数, 可以将DataFrame的行…...

C#,数值计算——完全VEGAS编码的蒙特·卡洛计算方法与源程序
1 文本格式 using System; namespace Legalsoft.Truffer { /// <summary> /// Complete VEGAS Code /// adaptive/recursive Monte Carlo /// </summary> public abstract class VEGAS { const int NDMX 50; const int …...

纯css实现3D鼠标跟随倾斜
老规矩先上图 为什么今天会想起来整这个呢?这是因为和我朋友吵架, 就是关于这个效果的,就是这个 卡片懸停毛玻璃效果, 我朋友认为纯css也能写, 我则坦言他就是在放狗屁,这种跟随鼠标的3D效果要怎么可能能用纯css写, 然后吵着吵着发现,欸,好像真能用css写哦,我以前还写过这种…...

Pandas数据结构
文章目录 1. Series数据结构1.1 Series数据类型创建1.2 Series的常用属性valuesindex/keys()shapeTloc/iloc 1.3 Series的常用方法mean()max()/min()var()/std()value_counts()describe() 1.4 Series运算加/减法乘法 2. DataFrame数据结构2.1 DataFrame数据类型创建2.2 布尔索引…...

systemverilog function的一点小case
关于function的应用无论是在systemverilog还是verilog中都有很广泛的应用,但是一直有一个模糊的概念困扰着我,今天刚好有时间来搞清楚并记录下来。 关于fucntion的返回值的问题: function integer clog2( input logic[255:0] value);for(cl…...

微服务的初步使用
环境说明 jdk1.8 maven3.6.3 mysql8 idea2022 spring cloud2022.0.8 微服务案例的搭建 新建父工程 打开IDEA,File->New ->Project,填写Name(工程名称)和Location(工程存储位置),选…...
【2023年11月第四版教材】第18章《项目绩效域》(合集篇)
第18章《项目绩效域》(合集篇) 1 章节内容2 干系人绩效域2.1 绩效要点2.2 执行效果检查2.3 与其他绩效域的相互作用 3 团队绩效域3.1 绩效要点3.2 与其他绩效域的相互作用3.3 执行效果检查3.4 开发方法和生命周期绩效域 4 绩效要点4.1 与其他绩效域的相互…...

Android 11.0 mt6771新增分区功能实现三
1.前言 在11.0的系统开发中,在对某些特殊模块中关于数据的存储方面等需要新增分区来保存, 所以就需要在系统分区新增分区,接下来就来实现这个功能,看系列三的实现过程 2.mt6771新增分区功能实现三的核心类 build/make/tools/releasetools/common.py device/mediatek/mt6…...
计算机网络——计算机网络的性能指标(上)-速率、带宽、吞吐量、时延
目录 速率 比特 速率 例1 带宽 带宽在模拟信号系统中的意义 带宽在计算机网络中的意义 吞吐量 时延 发送时延 传播时延 处理时延 例2 例3 速率 了解速率之前,先详细了解一下比特: 比特 计算机中数据量的单位,也是信息论中信…...
)
每日一题 518零钱兑换2(完全背包)
题目 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带符号整…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...
