【剑指Offer】13.机器人的运动范围
题目
地上有一个 rows 行和 cols 列的方格。坐标从 [0,0] 到 [rows-1,cols-1] 。一个机器人从坐标 [0,0] 的格子开始移动,每一次只能向左,右,上,下四个方向移动一格,但是不能进入行坐标和列坐标的数位之和大于 threshold 的格子。 例如,当 threshold 为 18 时,机器人能够进入方格 [35,37] ,因为 3+5+3+7 = 18。但是,它不能进入方格 [35,38] ,因为 3+5+3+8 = 19 。请问该机器人能够达到多少个格子?
数据范围:0≤threshold≤15 ,1≤rows,cols≤100
进阶:空间复杂度 O(nm) ,时间复杂度 O(nm)
示例1
输入:1,2,3
返回值:3
示例2
输入:0,1,3
返回值:1
示例3
输入:10,1,100
返回值:29
说明:[0,0],[0,1],[0,2],[0,3],[0,4],[0,5],[0,6],[0,7],[0,8],[0,9],[0,10],[0,11],[0,12],[0,13],[0,14],[0,15],[0,16],[0,17],[0,18],[0,19],[0,20],[0,21],[0,22],[0,23],[0,24],[0,25],[0,26],[0,27],[0,28] 这29种,后面的[0,29],[0,30]以及[0,31]等等是无法到达的
示例4
输入:5,10,10
返回值:21
解答
源代码
import java.util.*;public class Solution {public int movingCount(int threshold, int rows, int cols) {boolean[][] flag = new boolean[rows][cols];return dfs(threshold, rows, cols, 0, 0, flag);}public int dfs(int threshold, int rows, int cols, int i, int j, boolean[][] flag) {if (i < 0 || i >= rows || j < 0 || j >= cols || flag[i][j] || cal(i) + cal(j) > threshold) {return 0;}flag[i][j] = true;return 1 + dfs(threshold, rows, cols, i - 1, j, flag)+ dfs(threshold, rows, cols, i + 1, j, flag)+ dfs(threshold, rows, cols, i, j - 1, flag)+ dfs(threshold, rows, cols, i, j + 1, flag);}public int cal(int number) {int sum = 0;while (number != 0) {sum += number % 10;number /= 10;}return sum;}
}
总结
迷宫问题,回溯就完事,记得做标记避免重复经过方格。
这里要注意求的是机器人的运动“范围”而不是一条最大路径,所以每次应该加上上下左右路径的所有长度,而不是只加上一条最长的路径。
相关文章:

【剑指Offer】13.机器人的运动范围
题目 地上有一个 rows 行和 cols 列的方格。坐标从 [0,0] 到 [rows-1,cols-1] 。一个机器人从坐标 [0,0] 的格子开始移动,每一次只能向左,右,上,下四个方向移动一格,但是不能进入行坐标和列坐标的数位之和大于 thresh…...
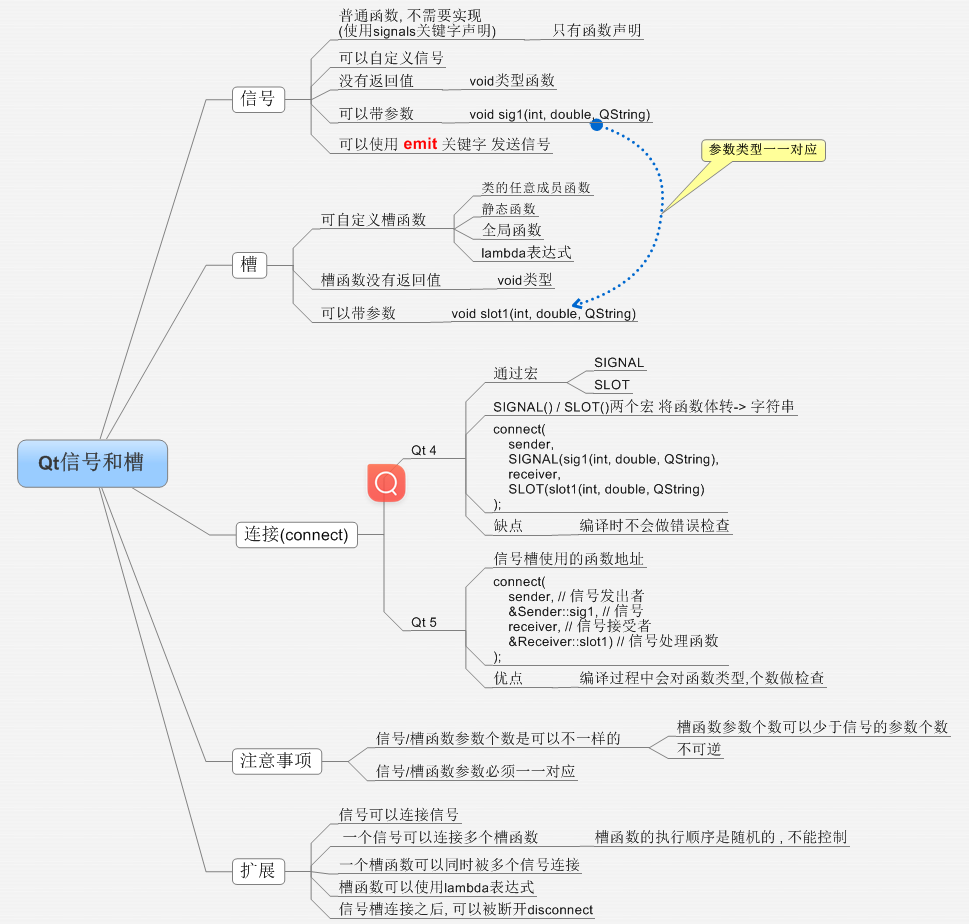
【Qt基础篇】信号和槽
文章目录 一些常见的bug:字符集不对产生的错误VS平台中文乱码 QT的优点关于.pro文件QtCreator快捷键最简单的qt程序按钮的创建对象模型**Qt窗口坐标**体系信号和槽机制connect函数系统自带的信号和槽案例:实现点击按钮-关闭窗口的案例 自定义信号和槽案例…...

.netCore用DispatchProxy实现动态代理
在 .NET Core 中,你可以使用 DispatchProxy 类来实现动态代理。DispatchProxy 允许你在运行时创建一个代理对象,该代理对象可以拦截对其所代理的对象的方法调用,并在方法调用前后执行自定义的逻辑。这在 AOP(面向切面编程…...
好奇喵 | Tor浏览器——访问.onion网址,揭开Dark Web的神秘面纱
前言 在之前的博客中: 1.Surface Web —> Deep Web —> Dark Web,我们解释了表层网络、深层网络等的相关概念; 2.Tor浏览器——层层剥开洋葱,我们阐述了Tor的历史和基本工作原理; 3.Tor浏览器…...
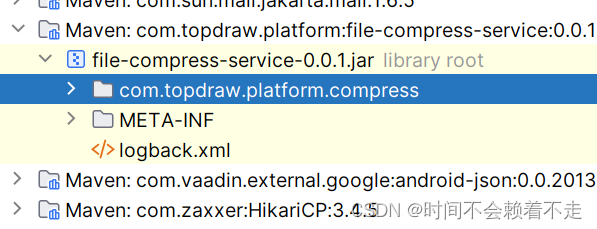
Maven 中引用其他项目jar包出现BOOT-INF问题
问题 在B项目中引入A项目的类,但是发现怎么也引入不进来 A项目打包之后,想在B项目中引用jar 在B项目中发现类文件无法引用 参考网上进行清缓存等一系列操作都没有解决。 最后发现引用的jar包中包含BOOT-INF, 然后去A项目中查找ÿ…...

PHP框架面试题
目录 1、什么是PHP框架? 2、常见的PHP框架有哪些? 3、为什么要使用PHP框架? 4、什么是路由?PHP框架中的路由是如何实现的? 5.TP的特性有哪些? 6.laravel有那些特点? 7.TP框架和Laravel框架的区别 8.tp5和tp6区…...
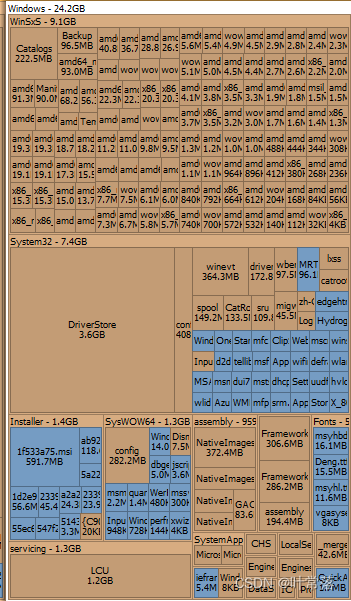
如何清理C盘
当前最棘手的问题是C盘满了,如何清理成了一个大问题,在本篇文章中我将记录我在清理c盘空间过程中的探索。 2023-10-06探索无果,记录于此。...

计算机网络基础知识
1 计算机网络是指将多台计算机连接在一起,以便它们可以相互通信和共享资源的系统。在本文中,我们将详细介绍计算机网络的基础知识,包括网络的分类、网络协议、网络拓扑、网络设备和网络安全等方面的内容。 网络分类 计算机网络可以根据其范…...
Go语言面经进阶10问
1.Golang可变参数 函数方法的参数,可以是任意多个,这种我们称之为可以变参数,比如我们常用的fmt.Println()这类函数,可以接收一个可变的参数。可以变参数,可以是任意多个。我们自己也可以定义可以变参数,可…...

大厂真题:【DP】米哈游2023秋招-米小游与魔法少女-奇运
题目描述与示例 题目描述 米小游都快保底了还没抽到希儿,好生气哦!只能打会活动再拿点水晶。 米小游和世界第一可爱的魔法少女 TeRiRi 正在打 BOSS,BOSS 的血量为h,当 BOSS 血量小于等于0时,BOSS 死亡。TeRiRi 有一…...
后端面经学习自测(一)
文章目录 1、MySQL-MVCC2、MySQL-原子性怎么实现3、MySQL-持久性怎么实现隔离性怎么实现 4、操作系统-死锁产生手写死锁死锁排查 5、操作系统-避免死锁死锁的四个必要条件预防死锁 6、操作系统-pageCache是什么零拷贝 7、计算机网络-TCP的可靠性和顺序性怎么实现8、计算机网络-…...

win10、win11安装Ubuntu 22.04
目前为止(2023年10月6日),最新的 Ubuntu 版本是 Ubuntu 22.04。你可以按照以下步骤在 Windows 上使用 WSL 安装 Ubuntu 22.04: 检查系统要求: 确保你的操作系统是 Windows 10 或更高版本,并已安装 Windows …...
golang gin框架1——简单案例以及api版本控制
gin框架 gin是golang的一个后台WEB框架 简单案例 package mainimport ("github.com/gin-gonic/gin""net/http" )func main() {r : gin.Default()r.GET("/ping", func(c *gin.Context) {//以json形式输出,还可以xml protobufc.JSON…...

Redisson—分布式对象
每个Redisson对象实例都会有一个与之对应的Redis数据实例,可以通过调用getName方法来取得Redis数据实例的名称(key)。 RMap map redisson.getMap("mymap"); map.getName(); // mymap 所有与Redis key相关的操作都归纳在RKeys这…...

alsa pcm接口之在unix环境的传输方法
在unix环境,数据片段响应被接受通过standard I/O call或事件等待路径(poll或select功能),为完成列表,异步通知响应该被列举出来.ALSA实现那些方法被描述在ALSA transfers部分. 标准I/O传输(Standadrd I/O transfers) 这个标准I/O传输常常使用read和write C语言函数集,对于那些函…...
小谈设计模式(20)—组合模式
小谈设计模式(20)—组合模式 专栏介绍专栏地址专栏介绍 组合模式对象类型叶节点组合节点 核心思想应用场景123 结构图结构图分析 Java语言实现首先,我们需要定义一个抽象的组件类 Component,它包含了组合节点和叶节点的公共操作&a…...

sheng的学习笔记-【中文】【吴恩达课后测验】Course 1 - 神经网络和深度学习 - 第三周测验
课程1_第3周_测验题 目录:目录 第一题 1.以下哪一项是正确的? A. 【 】 a [ 2 ] ( 12 ) a^{[2](12)} a[2](12)是第12层,第2个训练数据的激活向量。 B. 【 】X是一个矩阵,其中每个列都是一个训练示例。 C. 【 】 a 4 […...
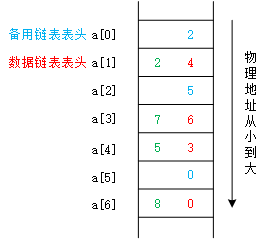
一文详解动态链表和静态链表的区别
1、引言 本文主要是对动态链表和静态链表的区别进行原理上的讲解分析,先通过对顺序表和动态链表概念和特点的原理性介绍,进而引申出静态链表的作用,以及其概念。通过这些原理性的概述,最后总结归纳出动态链表和静态链表的区别。本…...
[C国演义] 第十三章
第十三章 三数之和四数之和 三数之和 力扣链接 根据题目要求: 返回的数对应的下标各不相同三个数之和等于0不可包含重复的三元组 – – 即顺序是不做要求的 如: [-1 0 1] 和 [0, 1, -1] 是同一个三元组输出答案顺序不做要求 暴力解法: 排序 3个for循环 去重 — — N^3, …...
<二>Qt斗地主游戏开发:过场动画的实现
1. 过场动画效果 2. 思路分析 过场动画较为简单,只有一个进度条在进行滚动,因此实现起来不需要动画相关处理,仅需要图片和定时器设定,让进度条动起来即可。我们可以创建一个对话框,设定背景图片以及对话框透明无边框&a…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...
