小谈设计模式(20)—组合模式
小谈设计模式(20)—组合模式
- 专栏介绍
- 专栏地址
- 专栏介绍
- 组合模式
- 对象类型
- 叶节点
- 组合节点
- 核心思想
- 应用场景
- 1
- 2
- 3
- 结构图
- 结构图分析
- Java语言实现
- 首先,我们需要定义一个抽象的组件类 Component,它包含了组合节点和叶节点的公共操作:
- 然后,我们定义组合节点类 Composite,它实现了 Component 接口,并包含了一个子组件列表:
- 最后,我们定义叶节点类 Leaf,它也实现了 Component 接口,但它没有子节点:
- 现在,我们可以使用组合模式来创建一个树状结构并操作它:
- 运行上述代码,输出结果如下
- 总结
- 优缺点分析
- 优点
- 简化客户端代码
- 增加新的节点类型
- 方便地处理递归结构
- 缺点
- 可能会导致设计过于一般化
- 可能会增加系统的复杂性
专栏介绍
专栏地址
link
专栏介绍
主要对目前市面上常见的23种设计模式进行逐一分析和总结,希望有兴趣的小伙伴们可以看一下,会持续更新的。希望各位可以监督我,我们一起学习进步,加油,各位。
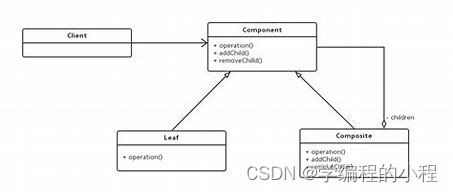
组合模式
组合模式是一种结构型设计模式,它允许将对象组合成树状结构以表示“部分-整体”的层次结构。组合模式使得客户端可以统一地处理单个对象和组合对象,无需区分它们的区别。
对象类型
叶节点(Leaf)和组合节点(Composite)
叶节点
它表示树的最底层的对象,它们没有子节点。
组合节点
它表示树的分支节点,它可以包含其他的组合节点和叶节点。
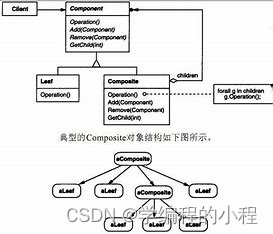
核心思想
使用一个抽象类或接口来定义组合节点和叶节点的公共操作。这样,客户端可以通过调用这些公共操作来处理组合节点和叶节点,而无需知道具体的节点类型。
应用场景
1
需要表示对象的部分-整体层次结构,并且希望客户端能够一致地处理单个对象和组合对象的情况。
2
需要对树状结构进行递归操作,例如遍历树、查找特定节点等。
3
需要动态地增加或删除树的节点。
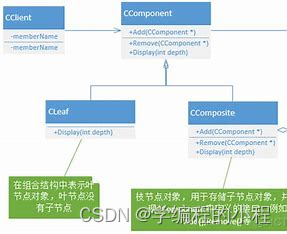
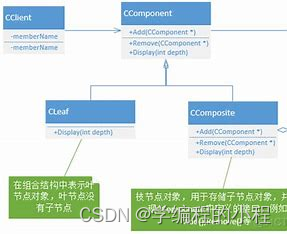
结构图
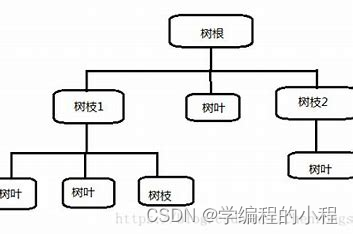
结构图分析
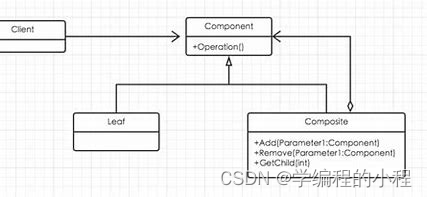
在上面的结构图中,Component 是组合模式的抽象类或接口,定义了组合节点和叶节点共有的操作。Composite 是组合节点的具体实现,它可以包含其他的组合节点和叶节点。Leaf 是叶节点的具体实现。
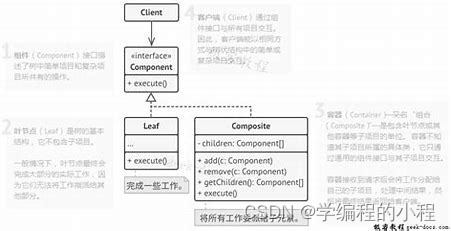
Java语言实现
首先,我们需要定义一个抽象的组件类 Component,它包含了组合节点和叶节点的公共操作:
public abstract class Component {protected String name;public Component(String name) {this.name = name;}public abstract void operation();public abstract void add(Component component);public abstract void remove(Component component);public abstract Component getChild(int index);
}
然后,我们定义组合节点类 Composite,它实现了 Component 接口,并包含了一个子组件列表:
import java.util.ArrayList;
import java.util.List;public class Composite extends Component {private List<Component> children;public Composite(String name) {super(name);children = new ArrayList<>();}@Overridepublic void operation() {System.out.println("Composite " + name + " operation.");for (Component component : children) {component.operation();}}@Overridepublic void add(Component component) {children.add(component);}@Overridepublic void remove(Component component) {children.remove(component);}@Overridepublic Component getChild(int index) {return children.get(index);}
}
最后,我们定义叶节点类 Leaf,它也实现了 Component 接口,但它没有子节点:
public class Leaf extends Component {public Leaf(String name) {super(name);}@Overridepublic void operation() {System.out.println("Leaf " + name + " operation.");}@Overridepublic void add(Component component) {// 叶节点不支持添加操作}@Overridepublic void remove(Component component) {// 叶节点不支持删除操作}@Overridepublic Component getChild(int index) {// 叶节点没有子节点return null;}
}
现在,我们可以使用组合模式来创建一个树状结构并操作它:
public class Main {public static void main(String[] args) {// 创建树状结构Composite root = new Composite("root");Composite branch1 = new Composite("branch1");Composite branch2 = new Composite("branch2");Leaf leaf1 = new Leaf("leaf1");Leaf leaf2 = new Leaf("leaf2");Leaf leaf3 = new Leaf("leaf3");root.add(branch1);root.add(branch2);branch1.add(leaf1);branch2.add(leaf2);branch2.add(leaf3);// 调用操作方法root.operation();}
}
运行上述代码,输出结果如下
Composite root operation.
Composite branch1 operation.
Leaf leaf1 operation.
Composite branch2 operation.
Leaf leaf2 operation.
Leaf leaf3 operation.
总结
以上就是使用Java语言实现组合模式的示例代码。通过组合模式,我们可以方便地处理树状结构,并且客户端可以一致地处理单个对象和组合对象。
优缺点分析
优点
简化客户端代码
客户端可以一致地处理单个对象和组合对象,无需区分它们的差异。
增加新的节点类型
通过继承 Component 类,可以方便地增加新的节点类型,而无需修改现有的代码。
方便地处理递归结构
组合模式适用于处理递归结构,例如树状结构。
缺点
可能会导致设计过于一般化
组合模式将叶节点和组合节点都抽象为 Component 类,可能会导致设计过于一般化,不适合特定的场景。
可能会增加系统的复杂性
组合模式引入了组合节点和叶节点的层次结构,可能会增加系统的复杂性。
相关文章:

小谈设计模式(20)—组合模式
小谈设计模式(20)—组合模式 专栏介绍专栏地址专栏介绍 组合模式对象类型叶节点组合节点 核心思想应用场景123 结构图结构图分析 Java语言实现首先,我们需要定义一个抽象的组件类 Component,它包含了组合节点和叶节点的公共操作&a…...

sheng的学习笔记-【中文】【吴恩达课后测验】Course 1 - 神经网络和深度学习 - 第三周测验
课程1_第3周_测验题 目录:目录 第一题 1.以下哪一项是正确的? A. 【 】 a [ 2 ] ( 12 ) a^{[2](12)} a[2](12)是第12层,第2个训练数据的激活向量。 B. 【 】X是一个矩阵,其中每个列都是一个训练示例。 C. 【 】 a 4 […...
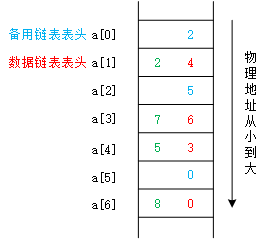
一文详解动态链表和静态链表的区别
1、引言 本文主要是对动态链表和静态链表的区别进行原理上的讲解分析,先通过对顺序表和动态链表概念和特点的原理性介绍,进而引申出静态链表的作用,以及其概念。通过这些原理性的概述,最后总结归纳出动态链表和静态链表的区别。本…...
[C国演义] 第十三章
第十三章 三数之和四数之和 三数之和 力扣链接 根据题目要求: 返回的数对应的下标各不相同三个数之和等于0不可包含重复的三元组 – – 即顺序是不做要求的 如: [-1 0 1] 和 [0, 1, -1] 是同一个三元组输出答案顺序不做要求 暴力解法: 排序 3个for循环 去重 — — N^3, …...
<二>Qt斗地主游戏开发:过场动画的实现
1. 过场动画效果 2. 思路分析 过场动画较为简单,只有一个进度条在进行滚动,因此实现起来不需要动画相关处理,仅需要图片和定时器设定,让进度条动起来即可。我们可以创建一个对话框,设定背景图片以及对话框透明无边框&a…...
)
链式法则(Chain Rule)
定义 链式法则(Chain Rule)是概率论和统计学中的一个基本原理,用于计算联合概率分布或条件概率分布的乘积。它可以用于分解一个复杂的概率分布为多个较简单的条件概率分布的乘积,从而简化概率分析问题。 链式法则有两种常见的形…...

AUTOSAR COM模块框架梳理
框架: COM的功能主要就是两个: 把IPDU内的signal提取出来提供给SWC使用,把SWC发送的signal拷贝到IPDU buffer内 所以,COM的关键字是 signal, signal group, IPDU, IPDU group Signal group 是为了保证 Complex Data Types 的数…...

详细介绍区块链之挖矿
对不起,大家,这篇文章对作者来说实在是太有意义和含金量了,作者想把它设置为关注博主才能见全文,请大家理解!如果觉得还是看不懂,抱歉耽误大家的时间,就请取消关注!!&…...
)
华为OD机试真题-路灯照明问题(Java/C++/Go/Python)
【华为OD机试真题】路灯照明问题(Java/C++/Go/Python) 题目描述 在一条笔直的公路上安装了N个路灯,从位置0开始安装,路灯之间间距固定为100米。 每个路灯都有自己的照明半径,请计算第一个路灯和最后一个路灯之间,无法照明的区间的长度和。 输入描述 第一行为一个数N…...

嵌入式技术面试基本规则
潜规则1:面试的本质不是考试,而是告诉面试官你会做什么 经验不够的小伙伴特别容易犯的一个错误,不清楚面试官到底想问什么,其实整个面试中面试官并没有想难倒你的意思,只是想通过提问的方式来知道你会什么。 比如stm…...
osg实现自定义插件读取自定义格式的模型文件到场景
目录 1. 前言 2. 预备知识 3. 工具、原料 4. 代码实现 1. 前言 osg提供了很多插件来读取模型文件到场景中,这些插件支持大约70种格式类型的文件,但现实中的文件是各式各样,osg不可能囊括所有类型文件,当osg不支持某种类型格式…...

redis进阶
redis.conf 启动的时候就通过配置文件来启动的! # 这个不是配置的,就是在这儿说明一下 # 当配置中需要配置内存大小时,可以使用 1k, 5GB, 4M 等类似的格式,其转换方式如下(不区分大小写) # # 1k > 1000 bytes # 1kb > 102…...
(一)正点原子STM32MP135移植——准备
一、简述 使用板卡:正点原子的ATK-DLMP135 V1.2 从i.mx6ull学习完过来,想继续学习一下移植uboot和内核的,但是原子官方没有MP135的移植教程,STM32MP157的移植教程用的又是老版本的代码,ST官方更新后的代码不兼容老版本…...

Kotlin的关键字 lateinit 和 lazy
序、完善一下曾经的草稿。 Kotlin通常要求我们在定义属性后立即对起进行初始化,当我们不知道理想的初始值时,这样做似乎很奇怪,尤其是在生命周期驱动android属性的情况下。 lateinit 简介 lateinit,Kotlin提供的一个可以延迟初…...
阿里云服务器ECS详细介绍_云主机_服务器托管_弹性计算
阿里云服务器ECS英文全程Elastic Compute Service,云服务器ECS是一种安全可靠、弹性可伸缩的云计算服务,阿里云提供多种云服务器ECS实例规格,如经济型e实例、通用算力型u1、ECS计算型c7、通用型g7、GPU实例等,阿里云服务器网分享阿…...

12、建立健全人员培训体系
9、大小屏分离与精细化审核 10、质量审核的设立与合并 11、视频分类建议 内容仓为公司其他部门输送了许多人才,既包括有潜力的主管,也有表现突出或者具备某些特殊能力的员工,从内容仓走出的同事,有些已经成为公司重要业务某个方…...
代码随想录算法训练营第五十九天 | 647. 回文子串 516.最长回文子序列
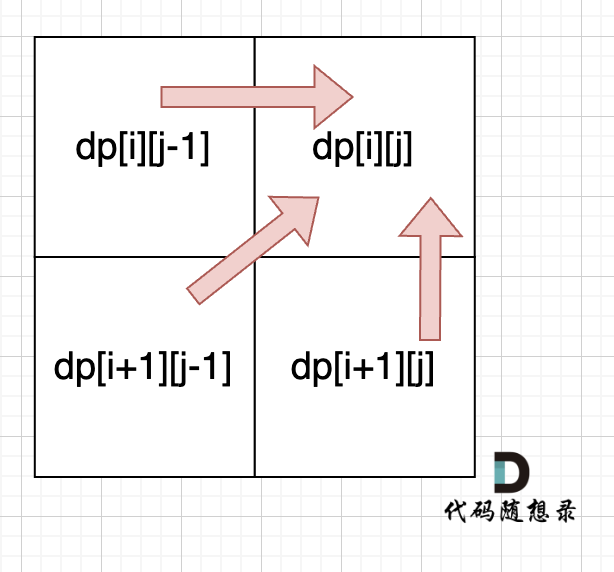
1. 回文子串 647. 回文子串 - 力扣(LeetCode) 一个子串左右两个元素相等,并且中间对称,才是回文子串 即 ij 时,[i1: j-1]对称 dp[i][j]: [i:j] 是否是回文字串 当 子串长度大于2 由 dp[i1][j-1] 推出…...

React Redux
redux是什么 Redux是一个模式和库,用于管理和更新应用程序状态,使用称为“action”的事件。它是需要在整个应用程序中使用的状态的集中存储,规则确保状态只能以可预测的方式更新。 Redux主要有三个功能: 获取当前状态更新状态监…...

StreamingLLM - 处理无限长度的输入
文章目录 关于 StreamingLLM使用关于 StreamingLLM Efficient Streaming Language Models with Attention Sinks GitHub : https://github.com/mit-han-lab/streaming-llm论文:https://arxiv.org/abs/2309.17453在流媒体应用程序(如多轮对话)中 部署大型语言模型(LLM)是迫…...

[Linux 命令] nm 详解
1. nm 命令: 显示关于指定 File 中符号的信息,文件可以是对象文件、可执行文件或对象文件库。如果文件没有包含符号信息,nm 命令报告该情况,但不把它解释为出错条件。 nm 命令缺省情况下报告十进制符号表示法下的数字值。 2. 命…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...
