链式法则(Chain Rule)
定义
链式法则(Chain Rule)是概率论和统计学中的一个基本原理,用于计算联合概率分布或条件概率分布的乘积。它可以用于分解一个复杂的概率分布为多个较简单的条件概率分布的乘积,从而简化概率分析问题。
链式法则有两种常见的形式:离散型和连续型。
-
离散型链式法则:假设有一系列随机变量 X 1 , X 2 , X 3 , . . . , X n X_1,X_2,X_3,...,X_n X1,X2,X3,...,Xn,链式法则可以表示为:
P ( X 1 , X 2 , X 3 , . . . , X n ) = P ( X 1 ) ∗ P ( X 2 ∣ X 1 ) ∗ P ( X 3 ∣ X 1 , X 2 ) ∗ . . . ∗ P ( X n ∣ X 1 , X 2 , X 3 , . . . , X n − 1 ) P(X_1, X_2, X_3, ..., X_n) = P(X_1) * P(X_2|X_1) * P(X_3|X_1, X_2) * ... * P(X_n|X_1, X_2, X_3, ..., X_{n-1}) P(X1,X2,X3,...,Xn)=P(X1)∗P(X2∣X1)∗P(X3∣X1,X2)∗...∗P(Xn∣X1,X2,X3,...,Xn−1)
这个公式说明了联合概率分布可以分解为一系列条件概率的乘积。从 X 1 X_1 X1到 X n X_n Xn,每个随机变量的条件概率都是在给定前面所有随机变量的条件下计算的。
-
连续型链式法则:对于连续型随机变量,链式法则可以表示为:
f ( x 1 , x 2 , x 3 , . . . , x n ) = f ( x 1 ) ∗ f ( x 2 ∣ x 1 ) ∗ f ( x 3 ∣ x 1 , x 2 ) ∗ . . . ∗ f ( x n ∣ x 1 , x 2 , x 3 , . . . , x n − 1 ) f(x_1, x_2, x_3, ..., x_n) = f(x_1) * f(x_2|x_1) * f(x_3|x_1, x_2) * ... * f(x_n|x_1, x_2, x_3, ..., x_{n-1}) f(x1,x2,x3,...,xn)=f(x1)∗f(x2∣x1)∗f(x3∣x1,x2)∗...∗f(xn∣x1,x2,x3,...,xn−1)
这个公式与离散型链式法则类似,但涉及到概率密度函数而不是概率质量函数。同样,每个随机变量的条件密度函数都是在给定前面所有随机变量的条件下计算的。
链式法则在概率推断、贝叶斯统计、机器学习和信息论等领域都有广泛的应用,它可以帮助分解复杂的联合分布,使问题变得更容易处理。
举例说明
让我们通过一个简单的例子来说明链式法则的应用。
假设有三个随机变量:A、B 和 C,它们表示以下事件:
- A 表示一个人是否患有心脏病(1表示患病,0表示不患病)。
- B 表示一个人是否吸烟(1表示吸烟,0表示不吸烟)。
- C 表示一个人是否有高胆固醇水平(1表示高胆固醇,0表示正常胆固醇水平)。
我们想计算患有心脏病的人中吸烟和高胆固醇的联合概率。根据链式法则,我们可以表示为:
P ( A = 1 , B = 1 , C = 1 ) = P ( A = 1 ) ∗ P ( B = 1 ∣ A = 1 ) ∗ P ( C = 1 ∣ A = 1 , B = 1 ) P(A=1, B=1, C=1) = P(A=1) * P(B=1|A=1) * P(C=1|A=1, B=1) P(A=1,B=1,C=1)=P(A=1)∗P(B=1∣A=1)∗P(C=1∣A=1,B=1)
这里的各个概率表示如下:
- P(A=1):心脏病的先验概率。
- P(B=1|A=1):在患有心脏病的条件下吸烟的条件概率。
- P(C=1|A=1, B=1):在患有心脏病且吸烟的条件下高胆固醇的条件概率。
如果我们已经有了这些概率的估计值,就可以使用链式法则来计算患有心脏病、吸烟和高胆固醇的人的联合概率。这个联合概率可以用于做出关于患病风险和健康行为的决策。
链式法则可以在更复杂的概率模型中应用,例如贝叶斯网络,以分解联合概率分布并进行推断和决策分析。这个例子只是一个简单的示例,用来说明链式法则的基本概念。
熵的链式法则
熵的链式法则用于计算多个随机变量的联合熵。如果有随机变量X1, X2, …, Xn,则它可以表示为:
H ( X 1 , X 2 , . . . , X n ) = H ( X 1 ) + H ( X 2 ∣ X 1 ) + H ( X 3 ∣ X 1 , X 2 ) + . . . + H ( X n ∣ X 1 , X 2 , . . . , X n − 1 ) H(X_1, X_2, ..., X_n) = H(X_1) + H(X_2|X_1) + H(X_3|X_1, X_2) + ... + H(X_n|X_1, X_2, ..., X_{n-1}) H(X1,X2,...,Xn)=H(X1)+H(X2∣X1)+H(X3∣X1,X2)+...+H(Xn∣X1,X2,...,Xn−1)
其中,H表示熵, H ( X 1 ) H(X_1) H(X1)是第一个随机变量X_1的熵, H ( X i ∣ X 1 , X 2 , . . . , X i − 1 ) H(X_i|X_1, X_2, ..., X_{i-1}) H(Xi∣X1,X2,...,Xi−1)是在给定前面的随机变量的条件下,随机变量X_i的条件熵。
相关文章:
)
链式法则(Chain Rule)
定义 链式法则(Chain Rule)是概率论和统计学中的一个基本原理,用于计算联合概率分布或条件概率分布的乘积。它可以用于分解一个复杂的概率分布为多个较简单的条件概率分布的乘积,从而简化概率分析问题。 链式法则有两种常见的形…...

AUTOSAR COM模块框架梳理
框架: COM的功能主要就是两个: 把IPDU内的signal提取出来提供给SWC使用,把SWC发送的signal拷贝到IPDU buffer内 所以,COM的关键字是 signal, signal group, IPDU, IPDU group Signal group 是为了保证 Complex Data Types 的数…...

详细介绍区块链之挖矿
对不起,大家,这篇文章对作者来说实在是太有意义和含金量了,作者想把它设置为关注博主才能见全文,请大家理解!如果觉得还是看不懂,抱歉耽误大家的时间,就请取消关注!!&…...
)
华为OD机试真题-路灯照明问题(Java/C++/Go/Python)
【华为OD机试真题】路灯照明问题(Java/C++/Go/Python) 题目描述 在一条笔直的公路上安装了N个路灯,从位置0开始安装,路灯之间间距固定为100米。 每个路灯都有自己的照明半径,请计算第一个路灯和最后一个路灯之间,无法照明的区间的长度和。 输入描述 第一行为一个数N…...

嵌入式技术面试基本规则
潜规则1:面试的本质不是考试,而是告诉面试官你会做什么 经验不够的小伙伴特别容易犯的一个错误,不清楚面试官到底想问什么,其实整个面试中面试官并没有想难倒你的意思,只是想通过提问的方式来知道你会什么。 比如stm…...
osg实现自定义插件读取自定义格式的模型文件到场景
目录 1. 前言 2. 预备知识 3. 工具、原料 4. 代码实现 1. 前言 osg提供了很多插件来读取模型文件到场景中,这些插件支持大约70种格式类型的文件,但现实中的文件是各式各样,osg不可能囊括所有类型文件,当osg不支持某种类型格式…...

redis进阶
redis.conf 启动的时候就通过配置文件来启动的! # 这个不是配置的,就是在这儿说明一下 # 当配置中需要配置内存大小时,可以使用 1k, 5GB, 4M 等类似的格式,其转换方式如下(不区分大小写) # # 1k > 1000 bytes # 1kb > 102…...
(一)正点原子STM32MP135移植——准备
一、简述 使用板卡:正点原子的ATK-DLMP135 V1.2 从i.mx6ull学习完过来,想继续学习一下移植uboot和内核的,但是原子官方没有MP135的移植教程,STM32MP157的移植教程用的又是老版本的代码,ST官方更新后的代码不兼容老版本…...

Kotlin的关键字 lateinit 和 lazy
序、完善一下曾经的草稿。 Kotlin通常要求我们在定义属性后立即对起进行初始化,当我们不知道理想的初始值时,这样做似乎很奇怪,尤其是在生命周期驱动android属性的情况下。 lateinit 简介 lateinit,Kotlin提供的一个可以延迟初…...
阿里云服务器ECS详细介绍_云主机_服务器托管_弹性计算
阿里云服务器ECS英文全程Elastic Compute Service,云服务器ECS是一种安全可靠、弹性可伸缩的云计算服务,阿里云提供多种云服务器ECS实例规格,如经济型e实例、通用算力型u1、ECS计算型c7、通用型g7、GPU实例等,阿里云服务器网分享阿…...

12、建立健全人员培训体系
9、大小屏分离与精细化审核 10、质量审核的设立与合并 11、视频分类建议 内容仓为公司其他部门输送了许多人才,既包括有潜力的主管,也有表现突出或者具备某些特殊能力的员工,从内容仓走出的同事,有些已经成为公司重要业务某个方…...
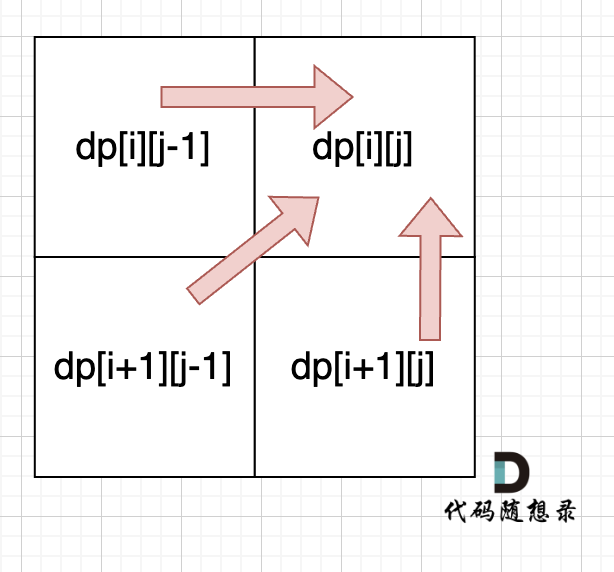
代码随想录算法训练营第五十九天 | 647. 回文子串 516.最长回文子序列
1. 回文子串 647. 回文子串 - 力扣(LeetCode) 一个子串左右两个元素相等,并且中间对称,才是回文子串 即 ij 时,[i1: j-1]对称 dp[i][j]: [i:j] 是否是回文字串 当 子串长度大于2 由 dp[i1][j-1] 推出…...

React Redux
redux是什么 Redux是一个模式和库,用于管理和更新应用程序状态,使用称为“action”的事件。它是需要在整个应用程序中使用的状态的集中存储,规则确保状态只能以可预测的方式更新。 Redux主要有三个功能: 获取当前状态更新状态监…...

StreamingLLM - 处理无限长度的输入
文章目录 关于 StreamingLLM使用关于 StreamingLLM Efficient Streaming Language Models with Attention Sinks GitHub : https://github.com/mit-han-lab/streaming-llm论文:https://arxiv.org/abs/2309.17453在流媒体应用程序(如多轮对话)中 部署大型语言模型(LLM)是迫…...

[Linux 命令] nm 详解
1. nm 命令: 显示关于指定 File 中符号的信息,文件可以是对象文件、可执行文件或对象文件库。如果文件没有包含符号信息,nm 命令报告该情况,但不把它解释为出错条件。 nm 命令缺省情况下报告十进制符号表示法下的数字值。 2. 命…...

好文学作品的鉴赏标准
好文学作品的鉴赏标准 2023年诺贝尔文学奖颁给了挪威剧作家约恩福瑟。由于之前的博彩公司给中国作家残雪开出了最高的赔率,以及诺贝尔官方推特在揭晓奖项前发布了一张泰戈尔99年前访华的老照片,残雪的获奖氛围在国内各类媒体的渲染下被拉至极高。当奖项…...

智慧公厕:将科技融入日常生活的创新之举
智慧公厕是当今社会中一项备受关注的创新项目。通过将科技融入公厕设计和管理中,这些公厕不仅能够提供更便利、更卫生的使用体验,还能够极大地提升城市形象和居民生活质量。本文将以智慧公厕领先厂家广州中期科技有限公司,大量的精品案例项目…...
ROS(0)命令及学习资源汇总
ROS安装命令 参考:Ubuntu20.04.4安装ROS Noetic详细教程 - 知乎 安装C和Python3 sudo apt-get install g sudo apt-get install python3 ROS运行小海龟仿真器 roscore确定ROS是否运行成功rosrun turtlesim turtlesim_node运行小海龟仿真器rosrun turtlesim turtle_…...

NodeMCU ESP8266开发流程详解(图文并茂)
文章目录 整体架构打开软件setuploop 连接开发板CP2102版本CH340版本 下载结论 整体架构 NodeMCU ESP8266基于Arduino IDE的开发相对来说还是比较容易上手的,我们基本需要以下几个东西; 一台安装好Arduino IDE的PC,并且已经部署环境&#x…...

【最终版】tkinter+matplotlib实现一个强大的绘图系统
文章目录 辅助坐标轴功能实现代码优化源代码 Python绘图系统: 前置源码: Python打造动态绘图系统📈一 三维绘图系统 📈二 多图绘制系统📈三 坐 标 轴 定 制📈四 定制绘图风格 📈五 数据生成导入…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...
