HashMap~
HashMap:
HashMap是面试中经常被问到的一个内容,以下两个经常被问到的问题,
Question1:底层数据结构,1.7和1.8有何不同?
答:1.7数组+链表,1.8数组+(链表|红黑树)
Question2:为何要用红黑树,为何一上来不树化,树化阈值为何是8,何时会转化,何时会退化为链表?
答: 红黑树用来避免 Dos 攻击,防止链表超长时性能下降,树化应当是偶然情况
hash 表的查找,更新的时间复杂度是 0(1),而红黑树的查找,更新的时间复杂度是 0(log2^n),TreeNode 占用空间也比普通 Node 的大,如非必要,尽量还是使用链表
hash 值如果足够随机,则在 hash 表内按泊松分布,在负载因子 0.75 的情况下,长度超过 8 的链表出现概率是0.00000006,选择8就是为了让树化几率足够小
树化两个条件:链表长度超过树化值;数组容量>=64
退化情况1:在扩容时,如果拆分树后,树元素个数<=6,则会退化链表
退化情况2: remove树节点之前,若 root、root.left、root.right、root.left.left 有一个为 null,也会退化为链表
如果你都可以回答出来,那么恭喜你不要高兴得太早,这只是开始,回答完之后面试官会进行一连串的追问,如果都没有回答出来,也不要过于沮丧,相信看完这篇文章会收获很多!
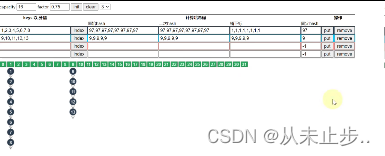
如下所示,我们将元素a放入Hashmap中,需要经历计算hash值,再和capacity进行求模再计算出桶下标
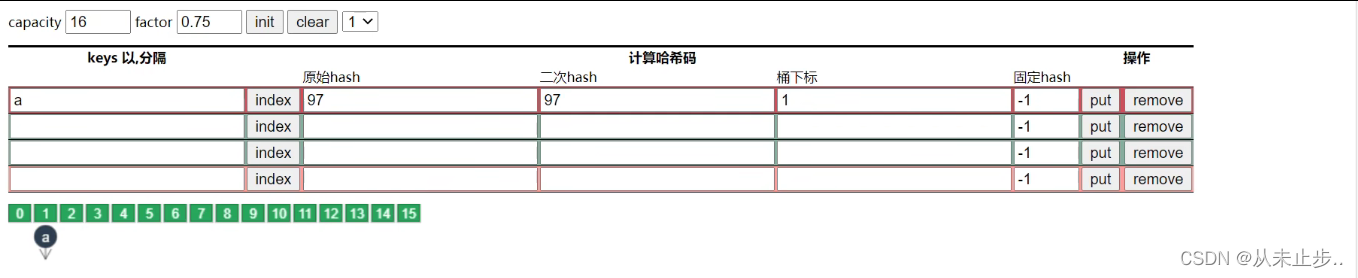 经过上述一系列的操作,相信不少的小伙伴会产生疑惑,到底有没有必要为了存储一个元素而通过这么复杂的步骤呢?
经过上述一系列的操作,相信不少的小伙伴会产生疑惑,到底有没有必要为了存储一个元素而通过这么复杂的步骤呢?
当然有必要,这样做是为了后续快速查找元素!
如下所示:
对于下述数组,我们将其放入Hashtable中,如果我们想查找元素a,那么需要比较10次才能够找到该元素
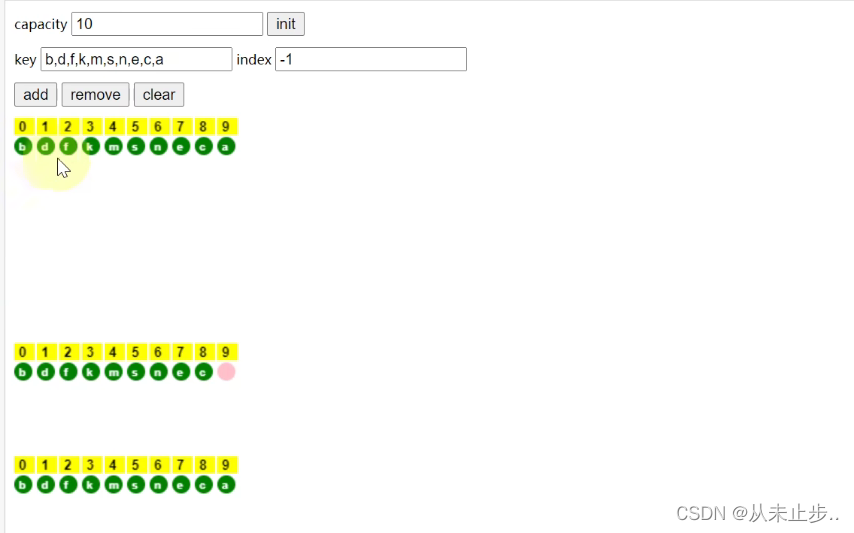
但如果将上述的数组的每个元素经过计算hash值,再和capacity进行求模再计算出桶下标,再放入HashMap中,如下所示:
此时我们如果想要查找元素a,那么可以直接通过计算桶下标进而确定元素a在下标为1的位置,这样我们只比较了一次。
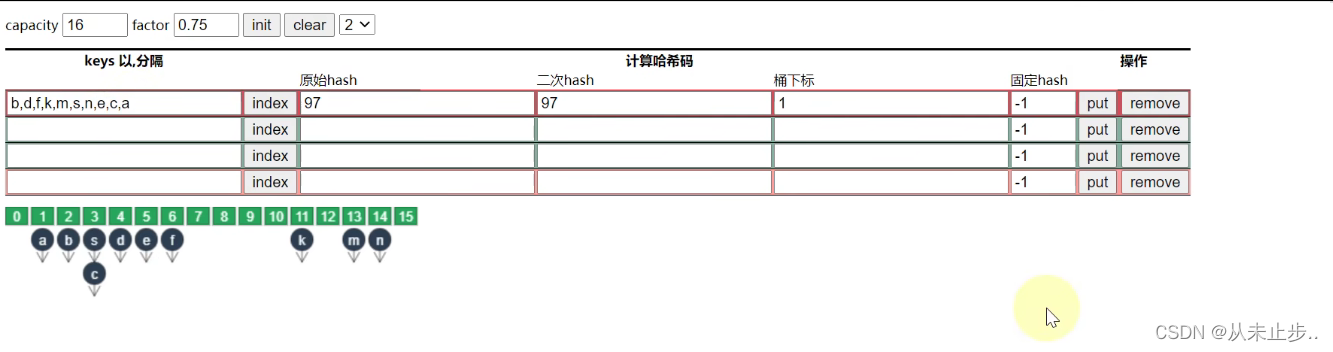
但上述这种是理想状态下,我们所查找的元素所处的下标只包含一个元素,此时的时间复杂度为O(1)
既然有最优情况,也就会有最极端的情况,如果当非常多的元素的桶下标计算出来都是相同的呢?
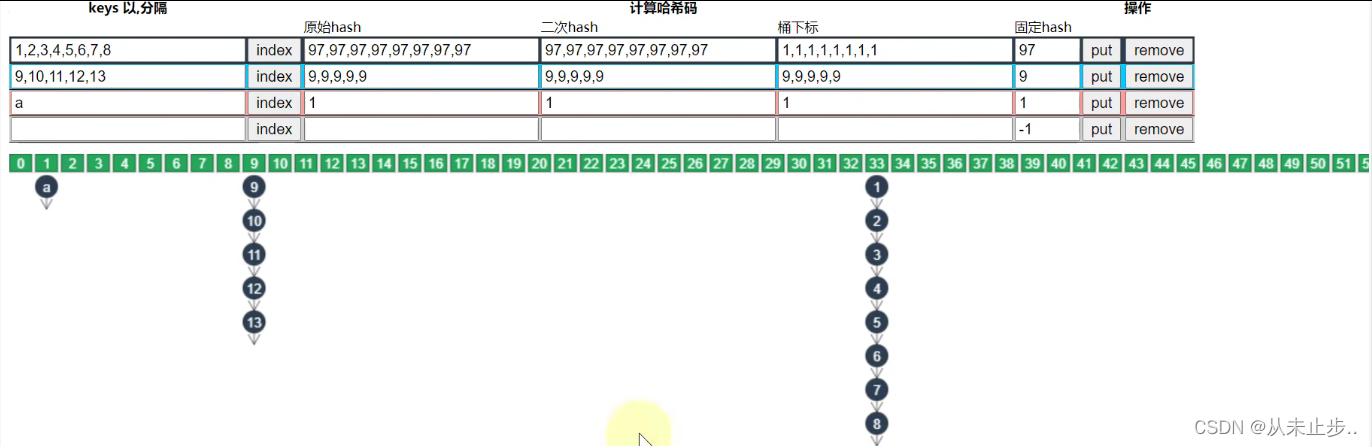
实例:

当我们想要查找元素8时,对于上述这种情况,即使计算出桶下标,但我们似乎还是需要比较8次,对此我们有两种解决思路-----------1:扩容,2:使用红黑树
使用扩容:
当元素的含量超过容器的3/4,就会进行扩容操作,如下所示:
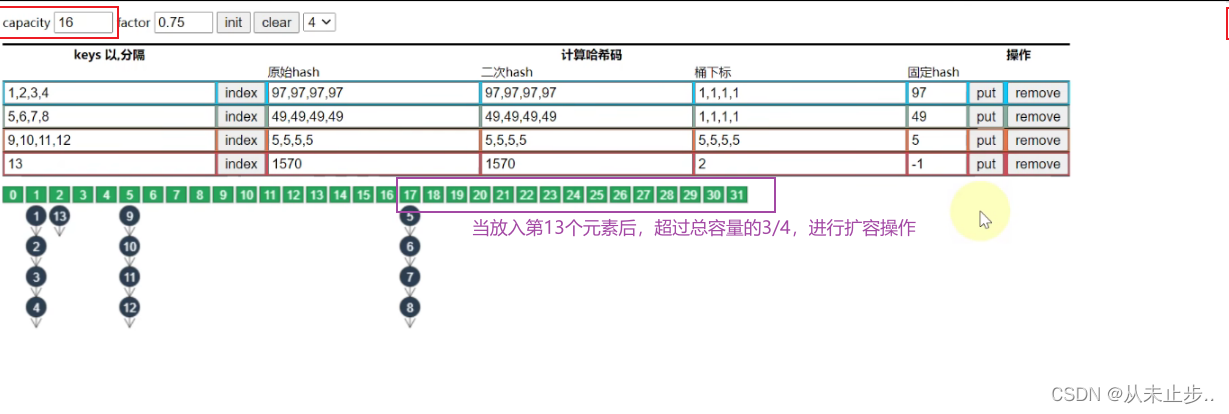
元素5,6,7,8的桶下标发生改变的原因为:此时的容量发生变化导致取模的结果也发方生变化,扩容后链表长度缩减
但扩容一定会导致链表长度的缩减吗?当然不是,当扩容后,没有元素桶下标的变化,自然就不会发生链表长度的缩减,如下所示:

对此,我们只有进行红黑树操作了
红黑树化:
当链表长度超过8并且总容量大于64,才会产生红黑树,而如果仅仅满足链表长度超过8时,会先通过扩容从而缩减链表长度,当扩容到64以后,才会红黑树化
举例:
当我强制性的将a添加到桶下标为1的位置时,此时即使链表长度超过了8,但也不会生成红黑树,而是优先进行扩容操作,如下所示:
继续向桶下标为33的地方添加元素,此时总容量大于64已经满足,且添加过后,该链表长度也超过8,因此会发生红黑树化
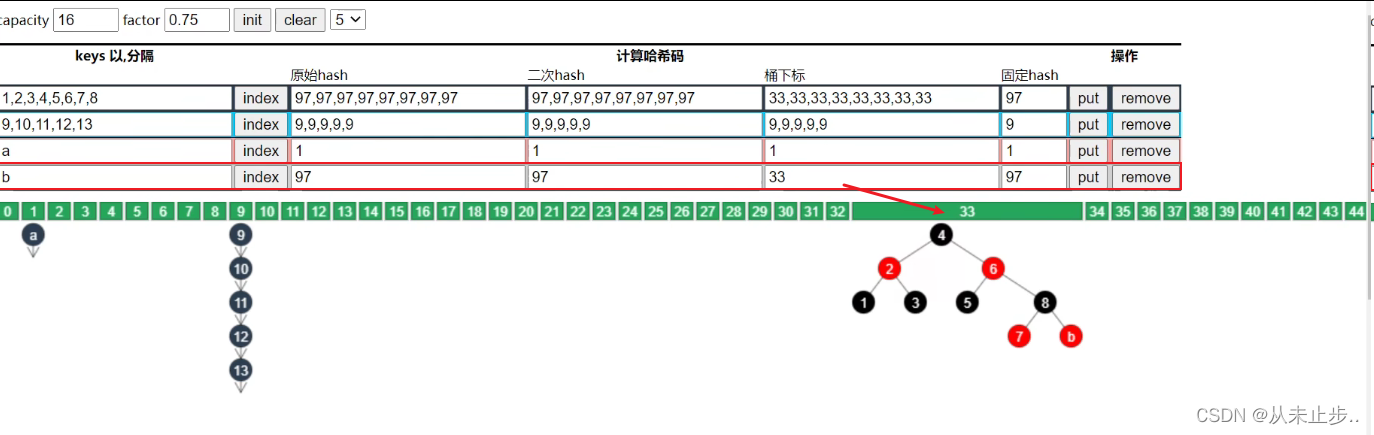
红黑树的特点:无论是根节点还是任意的子根节点都满足,(子)根节点左边的元素均小于(子)根节点,(子)根节点右边的元素均大于右(子)根节点
红黑树依然可以提高我们的查询效率,比如,此时我们需要查找元素8,那么只需要先确定元素8的桶下标,然后和4比较,再和6比较,最后和8比较,经过三次比较就可以找到元素8
链表的搜索时间复杂度为O(n),而红黑树的时间复杂度为O(log2^n)
注:某个桶下标的链表长度是可以超过8的,当总容量小于64时,并不会发生扩容,即使每次添加的桶下标为一个值,都不会红黑树化
索引的计算方法:
1:计算索引的hashCode(),再调用HashMap的hash()方法进行二次哈希,最后&(capacity-1)得到索引
2:二次hash()是为了综合高位数据,让哈希分布更为均匀
3:计算索引时,如果是2的n次幂可以使位与运算代替取模,效率更高,扩容时hash&oldCap==0的元素留在原来的位置,否则新位置=旧位置+oldCap
但1,2,3,都是为了配合容量为2的n次幂时的优化手段,例如:Hashtable的容量就不是2的n次幂,并不能说哪种设计更优,应该是设计者综合了各种因素,最终选择了使用2的n次幂作为容量
HashMap_put:
put方法流程,1.7和1.8有何不同?
1:HashMap是懒惰创建数组的,首次使用才创建数组
2:计算索引(桶下标)
3:如果桶下标还没人占用,创建Node占位返回
4:如果桶下标已经有人占用
1:已经是TreeNode走红黑树的添加或更新逻辑
2:是普通Node,走链表的添加或更新逻辑,如果链表长度超过树化阈值,走树化逻辑
5:返回前检查容量是否超过阈值,一旦超过则进行扩容
1.7 and1.8 的不同点:
链表插入节点时,1.7是头插法,1.8是尾插法
1.7是大于等于阈值且没有空位时才扩容,而1.8是大于阈值就扩容
1.8在扩容计算Node索引时,会优化---将哈希值与原来的哈希值进行按位与再判断
加载因子为何默认为0.75f?
在空间占用与查询时间之间取得较好的权衡
大于这个值,空间节省了,但链表就会比较长影响性能
小于这个值,冲突减少了,但扩容就会更频繁,空间占用多
多线程下会引发什么问题?
1.7:扩容死链
1.7和1.8数据错乱
扩容死锁的引发过程:
单线程下扩容的过程:
准备工作:

第一轮循环:
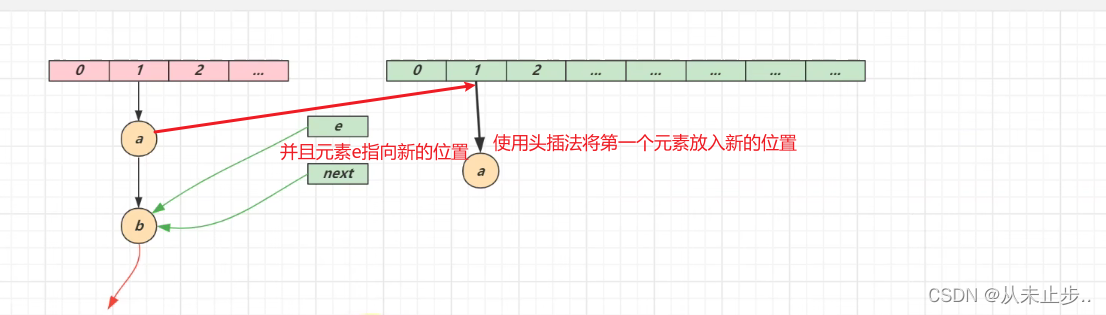
第二轮循环:
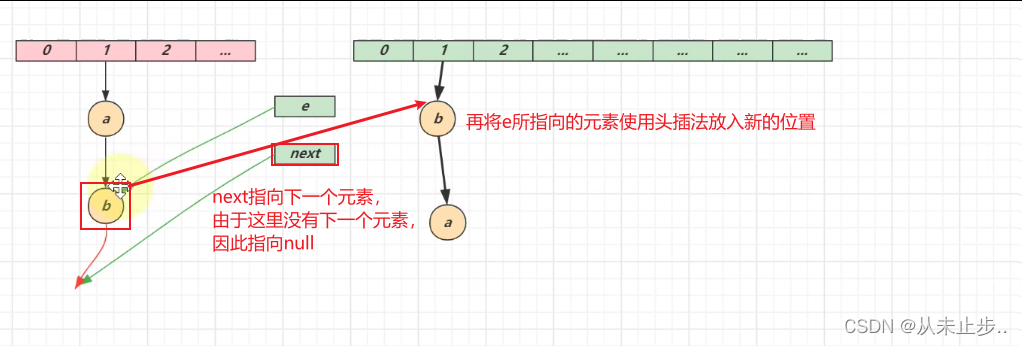
第二次循环结束,e指向下一个元素,进行第三次循环:
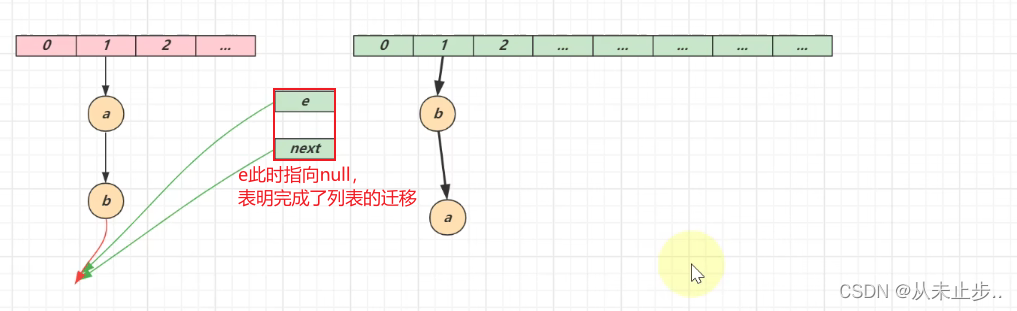
对象实现迁移并没有使得对象发生变化,只是对象的引用地址发生了变化,由于是头插法,因此使得迁移后的对象顺序发生了颠倒
多线程下扩容的过程:
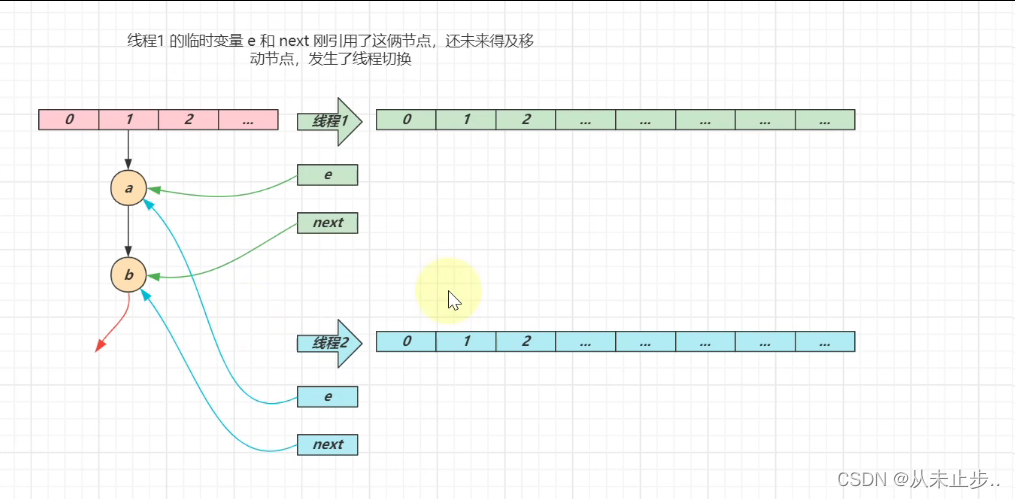
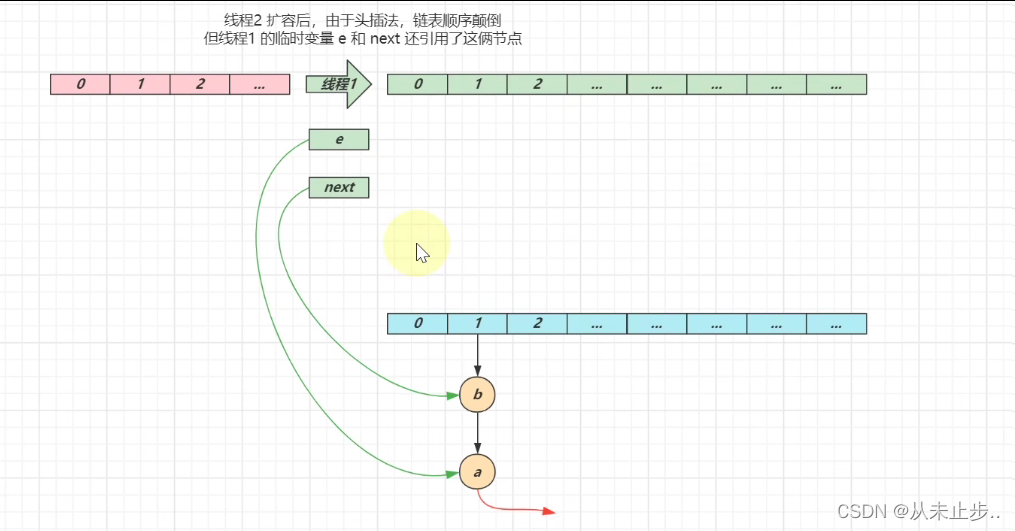
第一轮循环:
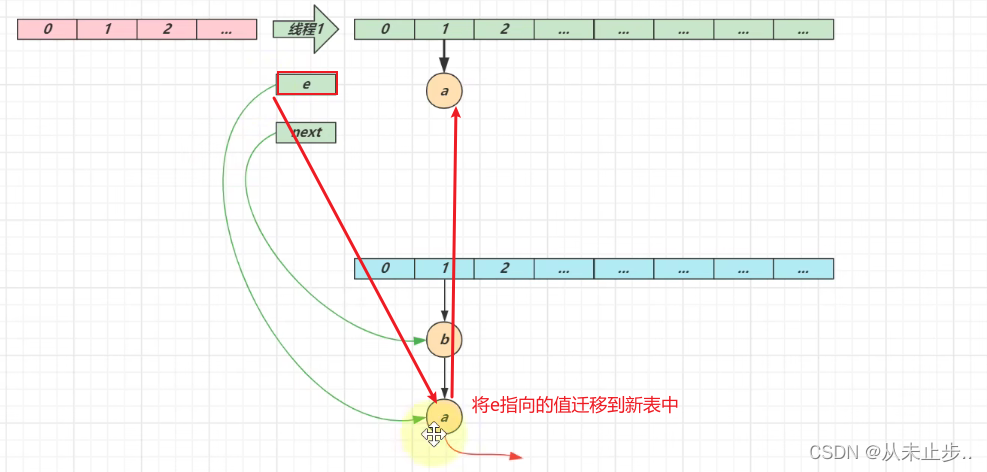
第一轮循环结束:
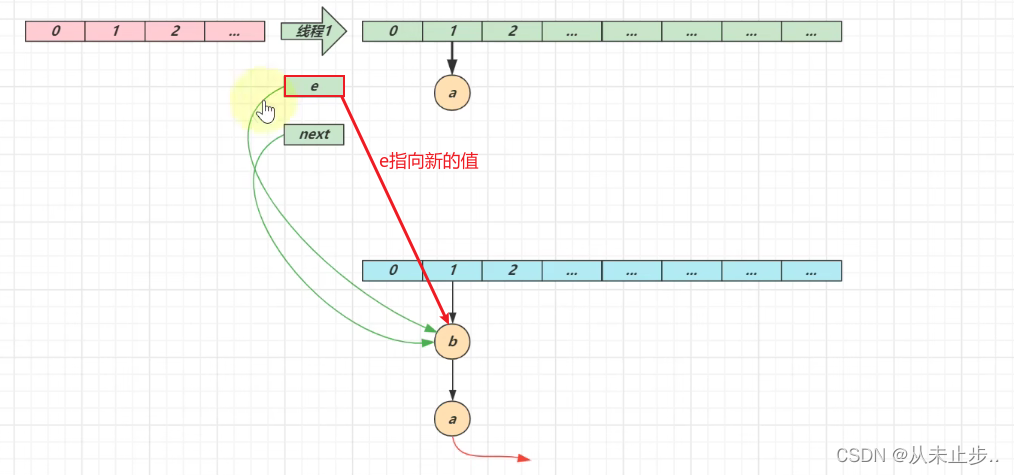
第二轮循环:
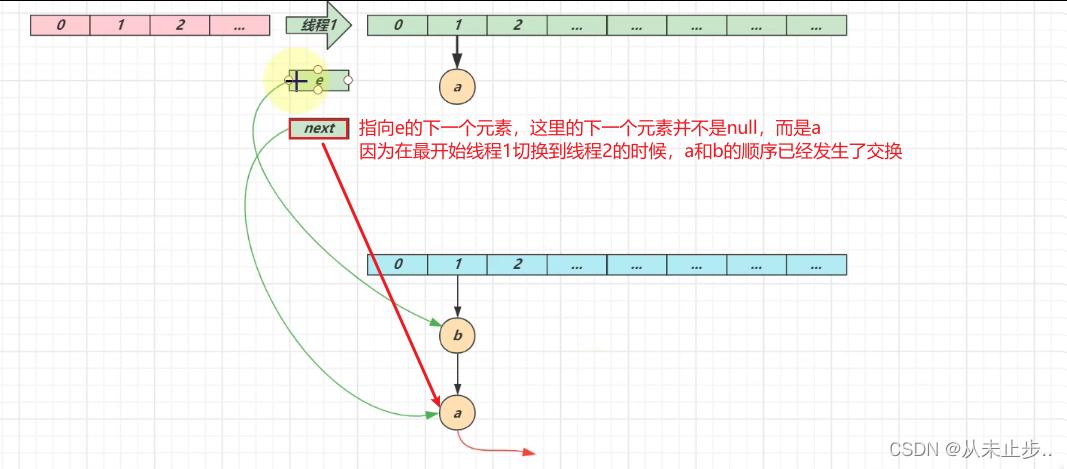
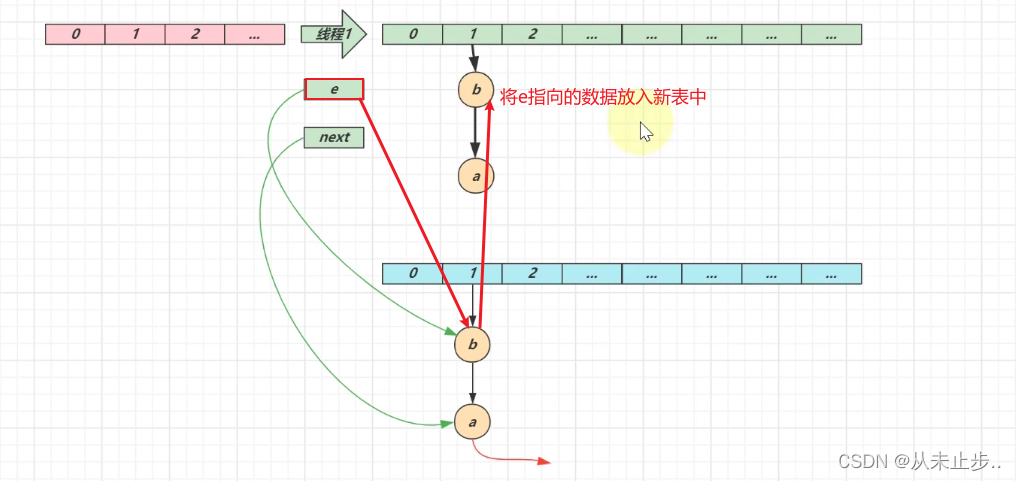
第二轮循环结束:
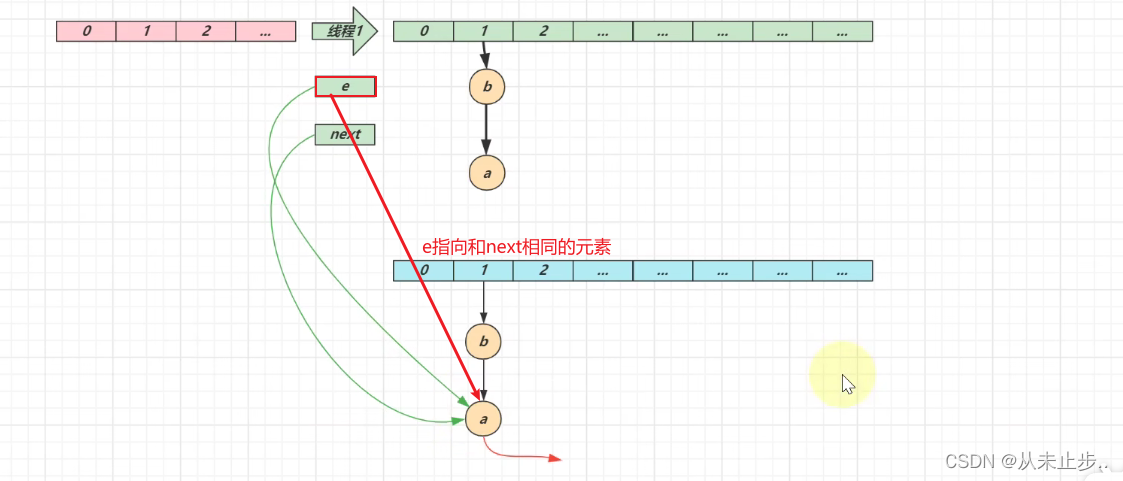
第三轮循环开始:
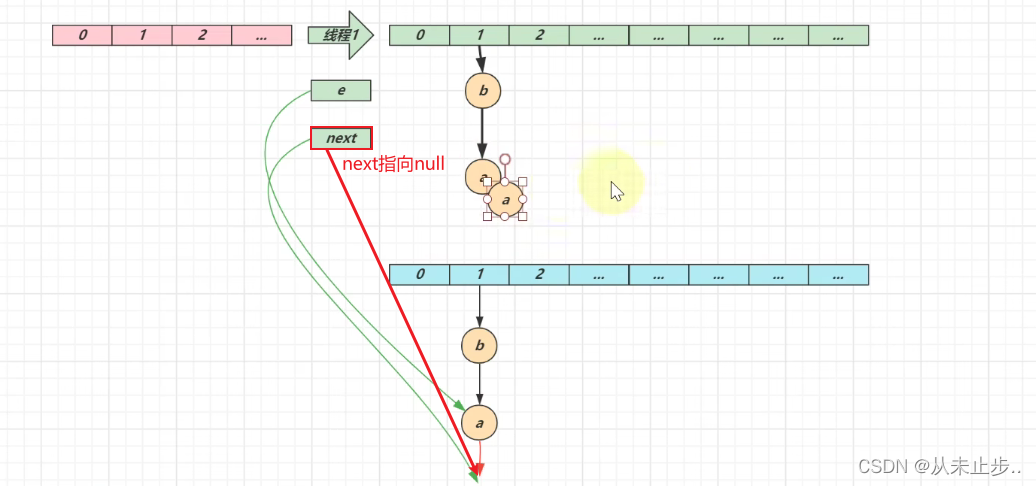
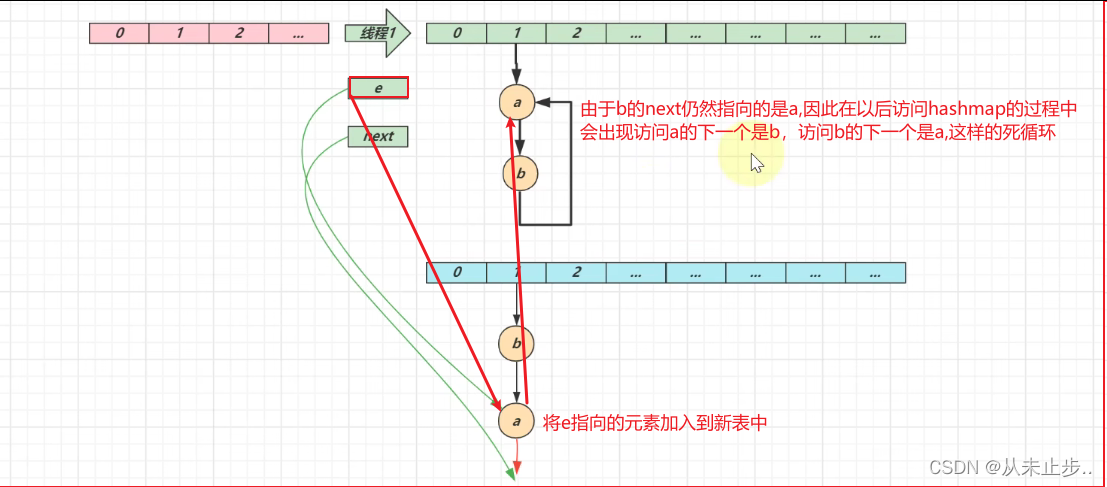
第三轮循环结束:
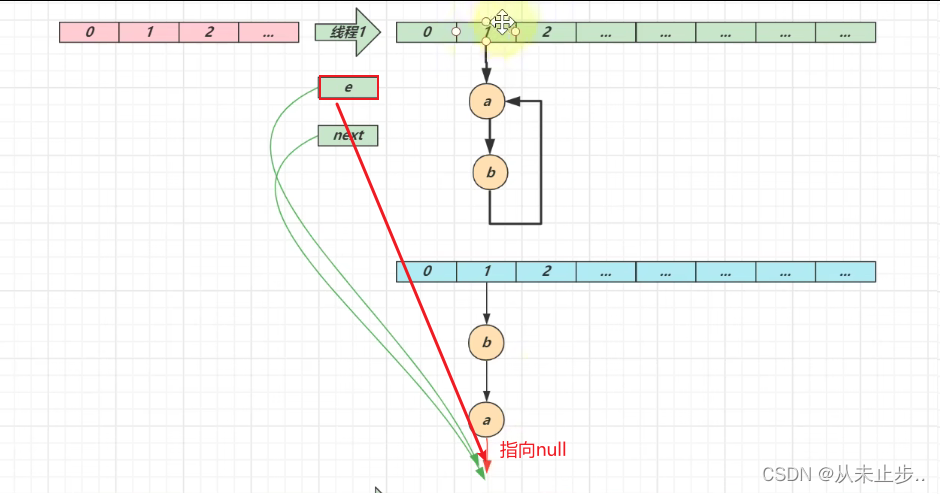
key能否为null,作为key的对象有什么要求?
HashMap的key可以作为null,但Map的其他实现则不然,比如treemap,作为key的对象,必须实现hashCode和equals,并且key的内容不能修改
不能修改的原因:
HashMap用Key的哈希值来存储和查找键值对,当插入一个Entry时,HashMap会计算Entry Key的哈希值,Map会根据这个哈希值把Entry插入到相应的位置,查找时,HashMap通过计算Key的哈希值到特定位置查找这个Entry,如果HashMap Key的哈希值在存储键值对后发生改变,Map可能再也查找不到这个Entry了,如果Key对象是可变的,那么Key的哈希值就可能改变,在HashMap中可变对象作为Key,会造成数据丢失,如果可变对象在HashMap中被用作键,那就要小心在改变对象状态的时候,不要改变它的哈希值了
必须实现hashCode和equals的原因:
如果只重写hashcode()不重写equals()方法,当比较equals()时,其实调用的是Object中的方法,只是看他们是否为同一对象(即进行内存地址的比较)
如果只重写equals()不重写hashcode()方法,在判断的时候,会被拦下HashMap认为是不同的Key,以对象作为HashMap的key,必须重写该对象的hashCode和equals方法,确保hashCode相等的时候equals的值也是true
String对象的hashCode()如何设计的,为什么每次乘的是31?
目的是达到较为均匀的散列效果,每个字符串的hashCode足够独特
字符串中的每个字符都可以表现为一个数字,称为Si,其中i的范围是0-n-1散列公式为:S0*31^ n-1+S1*31^ n-2......Si*31^ n-1-i+..........Sn-1*31^031带入公式有较好的散列特性,并且31*h可以被优化为:
1:即32*h-h
2:即2^5*h-h
3:即h<<5-h
举例:
公式套入31的散列效果如下:
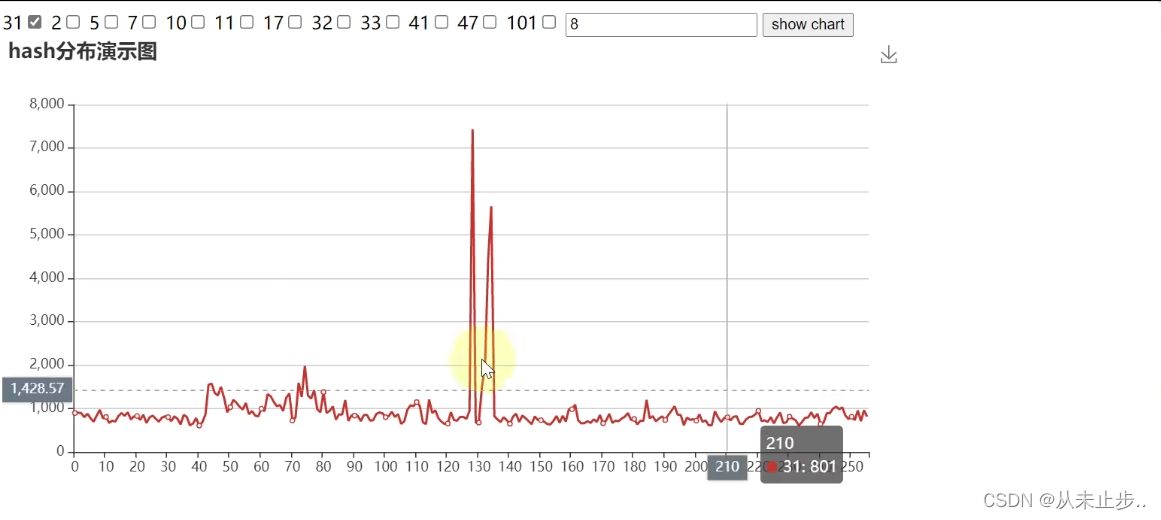
蓝色线条为公式套入2的散列效果如下:
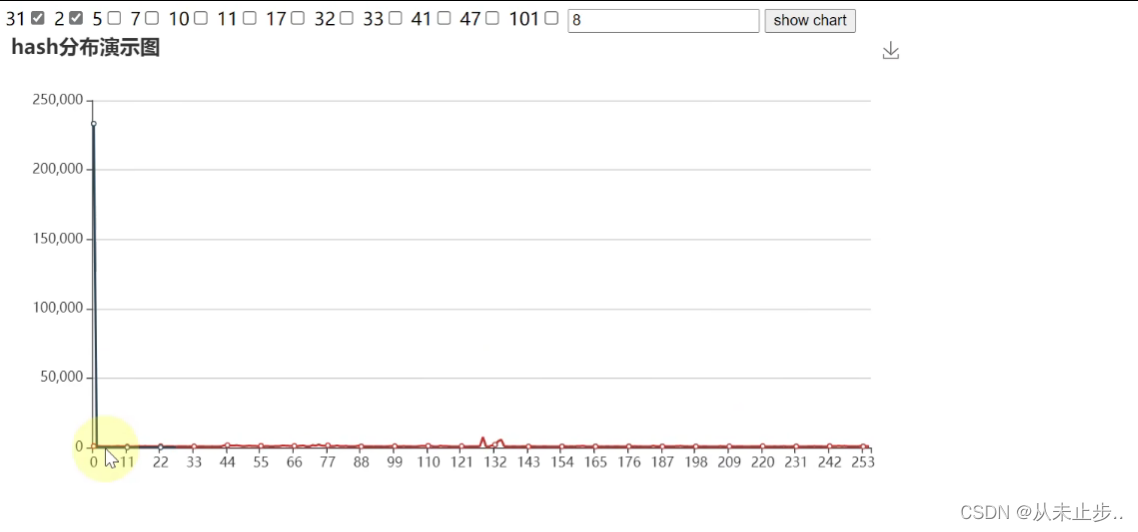
蓝色线条为公式套入11的散列效果如下:
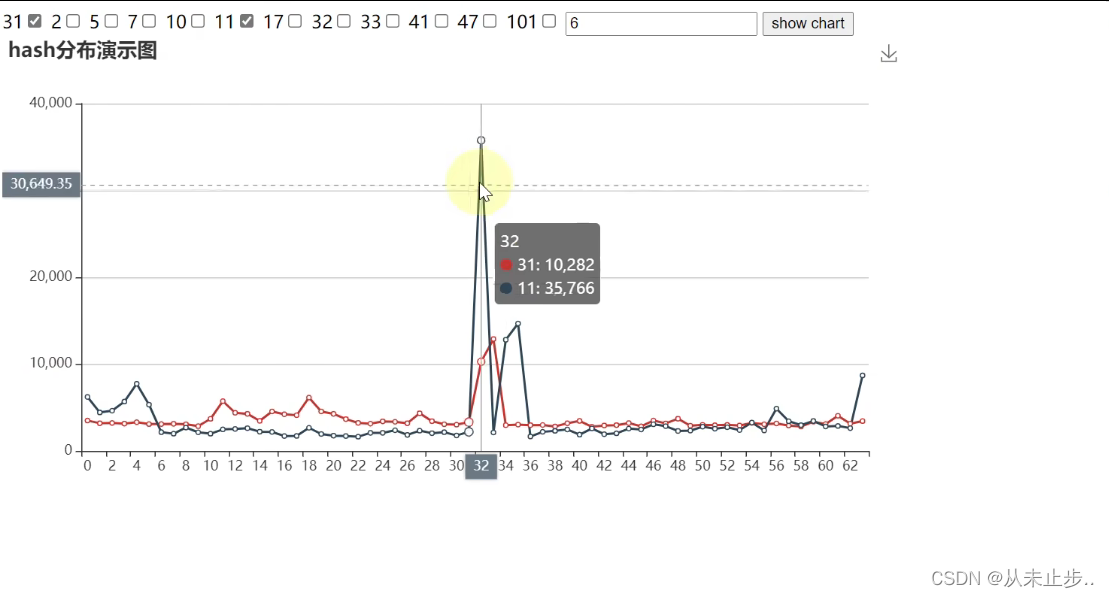
蓝色线条为公式套入41的散列效果如下:
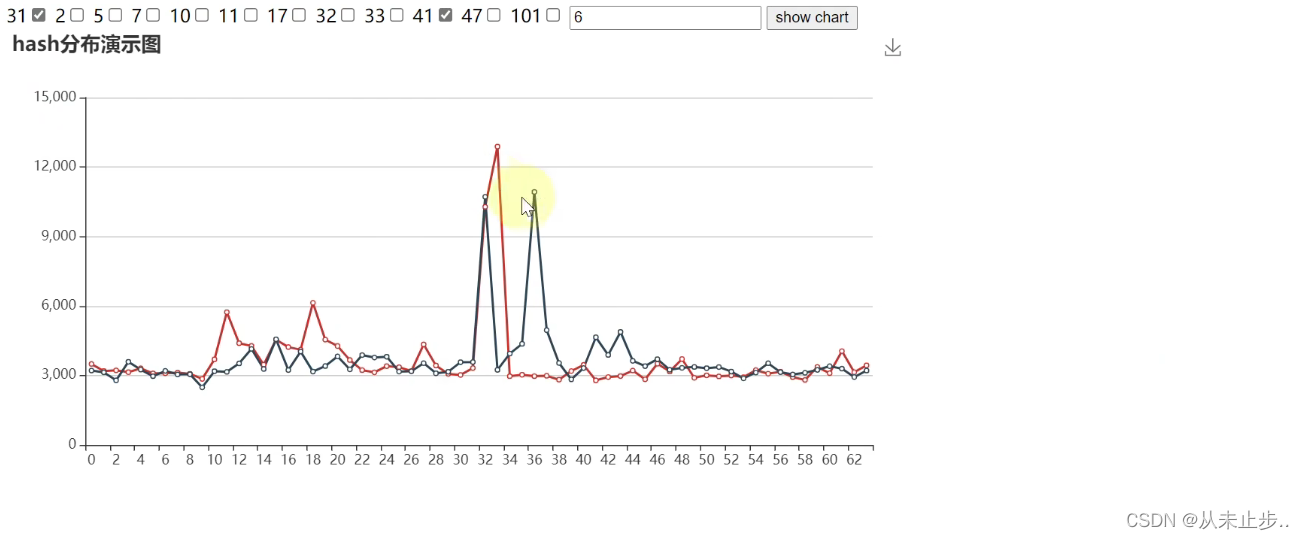
通过上述几组数据的对比,我们不难看出31和41套入公式的散列性是比较好的,那么为什么选择31而不是41呢?
原因是:我们不仅得保证有一个较好的散列性,而且还需要保证经过加减法可以优化为2的n次幂,31就满足,但41并不能满足
相关文章:

HashMap~
HashMap: HashMap是面试中经常被问到的一个内容,以下两个经常被问到的问题, Question1:底层数据结构,1.7和1.8有何不同? 答:1.7数组+链表,1.8数组+(链表|红…...
EasyNLP集成K-Global Pointer算法,支持中文信息抽取
作者:周纪咏、汪诚愚、严俊冰、黄俊 导读 信息抽取的三大任务是命名实体识别、关系抽取、事件抽取。命名实体识别是指识别文本中具有特定意义的实体,包括人名、地名、机构名、专有名词等;关系抽取是指识别文本中实体之间的关系;…...

mysql lesson3
DQL查找语句续集.............................. 分组函数(也叫多行处理函数) 1: select sum(sal) from emp;select min(sal)from emp;select max(sal)from emp;select avg(sal)from emp;select count(ename)from emp;2:分组函…...
python源码保护
文章目录代码混淆打包exe编译为字节码源码加密项目发布部署时,为防止python源码泄漏,可以通过几种方式进行处理代码混淆 修改函数、变量名 打包exe 通过pyinstaller 将项目打包为exe可执行程序,不过容易被反编译。 编译为字节码 py_comp…...

第51讲:SQL优化之COUNT查询的优化
文章目录 1.COUNT查询优化的概念2.COUNT函数的用法1.COUNT查询优化的概念 在很多的业务场景下可能需要统计一张表中的总数据量,当表的数据量很大时,使用COUNT统计表数据量时,也是非常耗时的。 MyISAM引擎会把一个表的总行记录在磁盘中,当执行count(*)的时候会直接从磁盘中…...

ArrayBlockingQueue
同步队列超出长度时,不同的返回形式可以分为以下四种。 会抛异常不会抛异常,有返回值死等,直到可以插入值或者取到值设置等待超时时间添加方法add()offfer()put()offer(E e,long timeout, TimeUnit unit)删除方法remove()poll()take()poll(l…...

DeepLabV3+:对预测处理的详解
相信大家对于这一部分才是最感兴趣的,能够实实在在的看到效果。这里我们就只需要两个.py文件(deeplab.py、predict_img.py)。 创建DeeplabV3类 deeplab.py的作用是为了创建一个DeeplabV3类,提供一个检测图片的方法,而…...
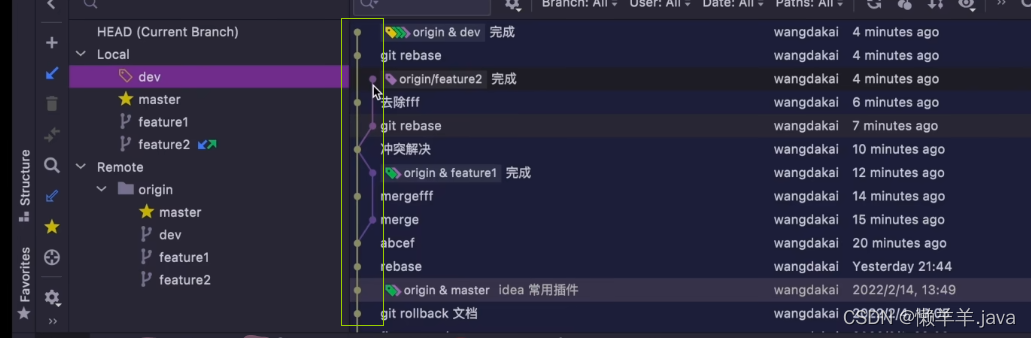
【Git】与“三年经验”就差个分支操作的距离
前言 Java之父于胜军说过,曾经一位“三年开发经验”的程序员粉丝朋友,刚入职因为不会解决分支问题而被开除,这是不是在警示我们什么呢? 针对一些Git的不常用操作,我们通过例子来演示一遍 1.版本回退 1.1已提交但未p…...
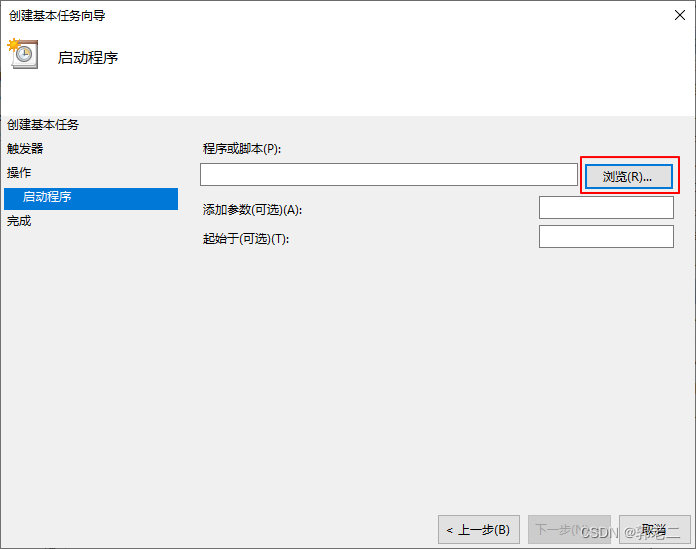
【经验】win10设置自启动
方法一:自启动文件夹 按下winr快捷键,弹出运行窗口,输入:shell:startup,弹出自启动文件夹窗口,将要开机自启的程序或快捷方式复制到此窗口中即可。 自启动文件夹路径:C:\Users\【用户名】\Ap…...

Linux SPI-NAND 驱动开发指南
文章目录Linux SPI-NAND 驱动开发指南1 概述1.1 编写目的1.2 适用范围1.3 相关人员3 流程设计3.1 体系结构3.2 源码结构3.3 关键数据定义3.3.1 flash 设备信息数据结构3.3.2 flash chip 数据结构3.3.3 aw_spinand_chip_request3.3.4 ubi_ec_hdr3.3.5 ubi_vid_hdr3.4 关键接口说…...
【THREE.JS学习(3)】使用THREEJS加载GeoJSON地图数据
本文接着系列文章(2)进行介绍,以VUE2为开发框架,该文涉及代码存放在HelloWorld.vue中。相较于上一篇文章对div命名class等,该文简洁许多。<template> <div></div> </template>接着引入核心库i…...

在windows搭建Redis集群并整合入Springboot项目
搭建集群配置规划Redis集群编写bat来启动每个redis服务安装Ruby安装Redis的Ruby驱动出现错误镜像过期SSL证书过期安装集群脚本redis-trib启动每个节点并执行集群构建脚本测试搭建是否成功配置springboot项目中配置规划Redis集群 我们搭建三个节点的集群,每个节点有…...

C++【内存管理】
文章目录C内存管理一、C/C内存分布1.1.C/C内存区域划分图解:1.2.根据代码进行内存区域分析二、C内存管理方式2.1.new/delete操作内置类型2.2.new和delete操作自定义类型三、operator new与operator delete函数四、new和delete的实现原理4.1.内置类型4.2.自定义类型4…...
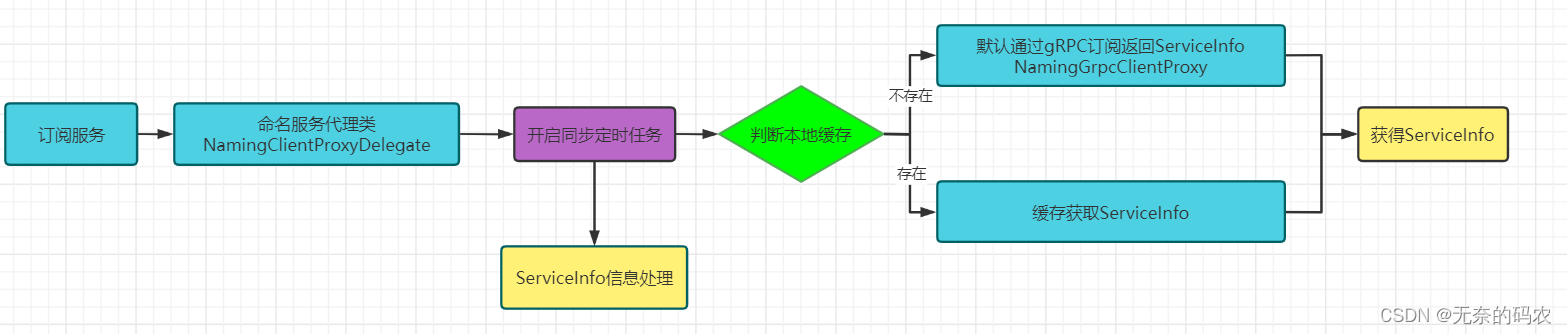
Spring Cloud Nacos源码讲解(六)- Nacos客户端服务发现
Nacos客户端服务发现源码分析 总体流程 首先我们先通过一个图来直观的看一下,Nacos客户端的服务发现,其实就是封装参数、调用服务接口、获得返回实例列表。 但是如果我们要是细化这个流程,会发现不仅包括了通过NamingService获取服务列表…...

华为OD机试题,用 Java 解【计算最大乘积】问题
最近更新的博客 华为OD机试 - 猴子爬山 | 机试题算法思路 【2023】华为OD机试 - 分糖果(Java) | 机试题算法思路 【2023】华为OD机试 - 非严格递增连续数字序列 | 机试题算法思路 【2023】华为OD机试 - 消消乐游戏(Java) | 机试题算法思路 【2023】华为OD机试 - 组成最大数…...

蓝牙运动耳机哪个好,比较好的运动蓝牙耳机
很多想选择蓝牙运动耳机的朋友都不知道应该如何选择,运动首先需要注意的就是耳机的防水能力以及耳机佩戴舒适度,在运动当中会排出大量的汗水,耳机防水等级做到越高,可以更好地保护耳机不受汗水浸湿,下面就分享五款适合…...

苹果设计可变色Apple Watch表带,智能穿戴玩法多
苹果最新技术专利显示,苹果正在为 Apple Watch 设计一款可变色的表带,可以根据佩戴者所穿着的服装、所在的环境等自动改变颜色。据介绍,这款表带里的灯丝具有电致变色功能,可以通过施加不同的电压,来实现显示多种颜色或…...

Elasticsearch集群Yellow亚健康状态修复
Elasticsearch集群Yellow亚健康状态修复问题背景排查流程解决办法问题背景 Elasticsearch集群健康状态为Yellow,涉及到多个索引。 排查流程 在浏览器打开Kibana Console进行问题排查,console地址为: http://{Kibana_IP}:5601/app/dev_too…...

第52讲:SQL优化之UPDATE更新操作的优化
文章目录 1.UPDATE更新语句的优化2.UPDATE更新语句优化案例1.UPDATE更新语句的优化 我们在使用UPDATE更新语句更改表中数据时,可能会导致表中产生行级锁或者是表级锁。 UPDATE语句的优化就是为了避免表中出现表级锁,从而影响并发的性能。 当UPDATE语句更新表数据时,WHERE…...
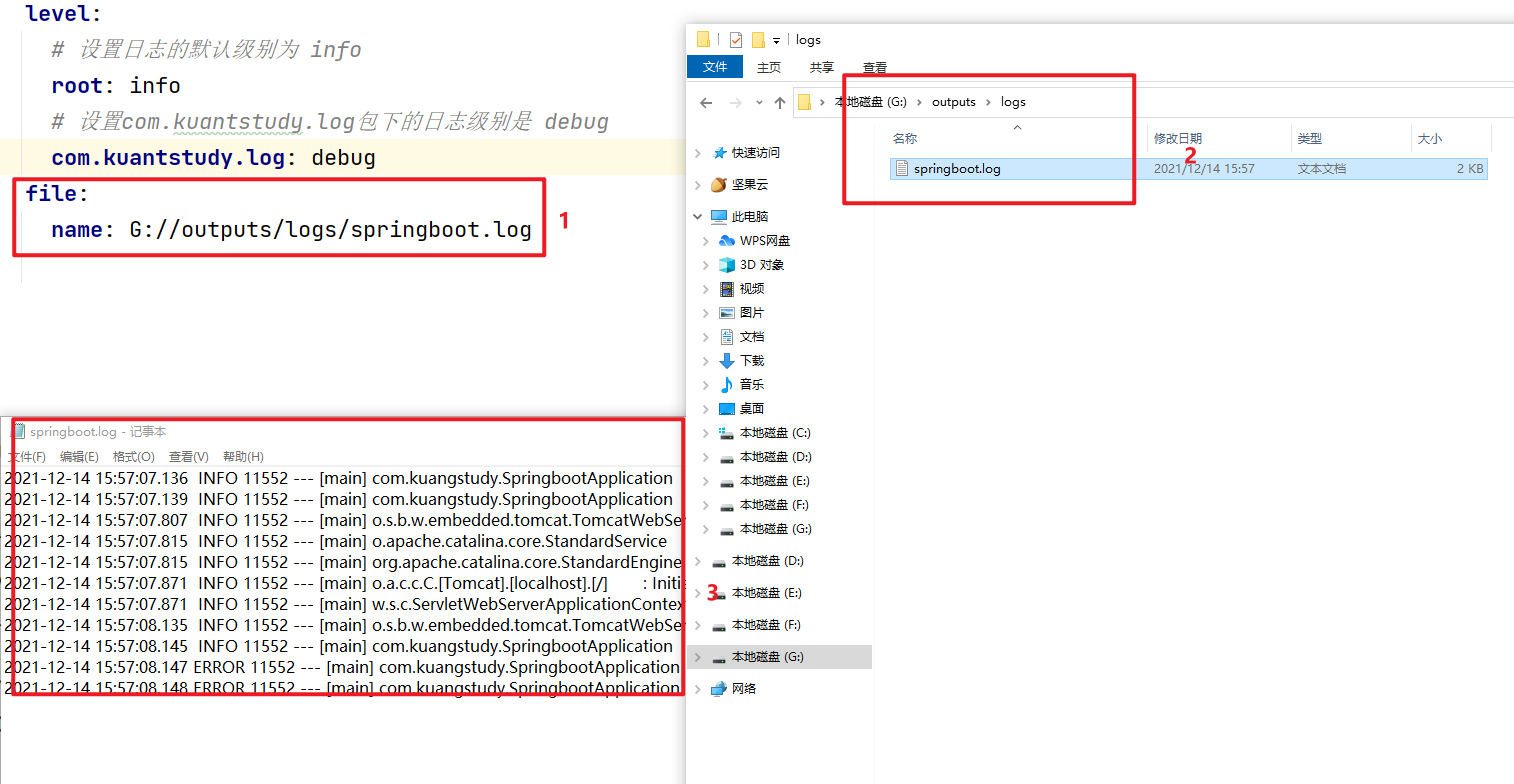
logback 自定义日志输出到数据库
项目日志格式 Spring Boot 的默认日志输出类似于以下示例: 2021-12-14 22:40:14.159 INFO 20132 --- [ main] com.kuangstudy.SpringbootApplication : Started SpringbootApplication in 2.466 seconds (JVM running for 3.617)输出以下项目&…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...
