《Dataset Condensation with Differentiable Siamese Augmentation》
《Dataset Condensation with Differentiable Siamese Augmentation》
在本文中,我们专注于将大型训练集压缩成显著较小的合成集,这些合成集可以用于从头开始训练深度神经网络,性能下降最小。受最近的训练集合成方法的启发,我们提出了可微暹罗增强方法,它可以有效地利用数据增强来合成更具信息的合成图像,从而在使用增强方法训练网络时获得更好的性能。在多个图像分类基准上的实验表明,该方法在CIFAR10和CIFAR100数据集上取得了较先进水平的显著提高,提高了7%。结果表明,该方法在MNIST、FashionMNIST、SVHN、CIFAR10上的相对性能分别为99.6%、94.9%、88.5%、71.5%,数据量不到1%。
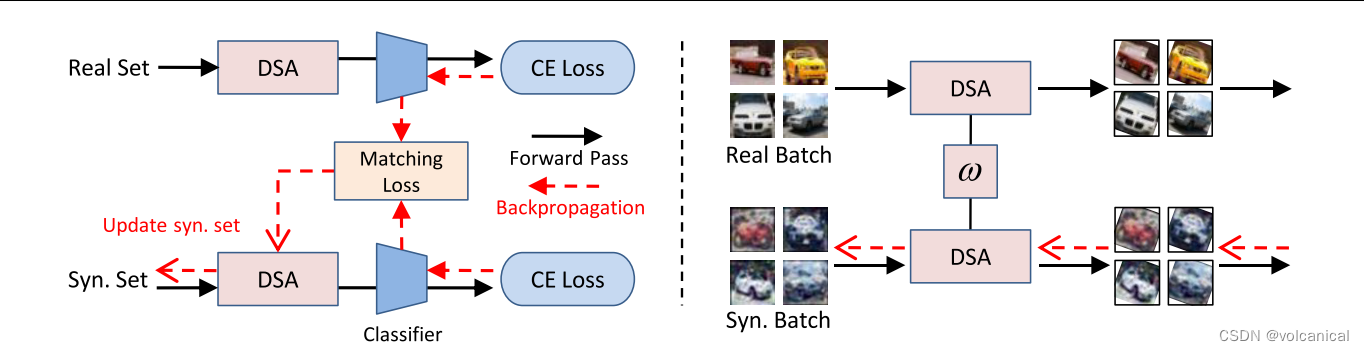
方法:
1. 简单介绍DC(Data Condensation)
假设我们有一个巨大的训练集 T = \mathcal{T}= T= { ( x 1 , y 1 ) , … , ( x ∣ T ∣ , y ∣ T ∣ ) } \left\{\left(\boldsymbol{x}_1, y_1\right), \ldots,\left(\boldsymbol{x}_{|\mathcal{T}|}, y_{|\mathcal{T}|}\right)\right\} {(x1,y1),…,(x∣T∣,y∣T∣)} 其中有 ∣ T ∣ |\mathcal{T}| ∣T∣ 个图片和标签对. DC (Zhao et al., 2021)目标是学习一个更小的数据集 ∣ S ∣ |\mathcal{S}| ∣S∣ 生成图片和标签对。 S = \mathcal{S}= S= { ( s 1 , y 1 ) , … , ( s ∣ S ∣ , y ∣ S ∣ ) } \left\{\left(\boldsymbol{s}_1, y_1\right), \ldots,\left(\boldsymbol{s}_{|\mathcal{S}|}, y_{|\mathcal{S}|}\right)\right\} {(s1,y1),…,(s∣S∣,y∣S∣)} 来自于(通过学习) T \mathcal{T} T 并且在数据集 S \mathcal{S} S 上训练的神经网络效果和在 T \mathcal{T} T 上训练得到的神经网络效果接近。 用 ϕ θ T \phi_{\boldsymbol{\theta}^{\mathcal{T}}} ϕθT 和 ϕ θ S \phi_{\boldsymbol{\theta}^{\mathcal{S}}} ϕθS 表示深度神经网络,其参数分别为 θ T \boldsymbol{\theta}^{\mathcal{T}} θT 和 θ S \boldsymbol{\theta}^{\mathcal{S}} θS,分别在训练集 T \mathcal{T} T 和 S \mathcal{S} S 上训练得到。DC的目标是如下方程:
E x ∼ P D [ ℓ ( ϕ θ τ ( x ) , y ) ] ≃ E x ∼ P D [ ℓ ( ϕ θ S ( x ) , y ) ] \begin{equation} \mathbb{E}_{\boldsymbol{x} \sim P_{\mathcal{D}}}\left[\ell\left(\phi_{\boldsymbol{\theta}^\tau}(\boldsymbol{x}), y\right)\right] \simeq \mathbb{E}_{\boldsymbol{x} \sim P_{\mathcal{D}}}\left[\ell\left(\phi_{\boldsymbol{\theta}^{\mathcal{S}}}(\boldsymbol{x}), y\right)\right] \end{equation} Ex∼PD[ℓ(ϕθτ(x),y)]≃Ex∼PD[ℓ(ϕθS(x),y)]
在真实数据分布 P D P_{\mathcal{D}} PD 上的损失 ℓ \ell ℓ (i.e. cross-entropy loss)。
在浓缩数据集 S \mathcal{S} S 上训练得到的模型参数要尽可能接近原始数据集的结果, i.e. θ S ≈ θ T \boldsymbol{\theta}^{\mathcal{S}} \approx \boldsymbol{\theta}^{\mathcal{T}} θS≈θT。
然后作者就开始举例DC有哪些不好的地方。
例如:
- 在每一轮都假设 θ t T \boldsymbol{\theta}^{\mathcal{T}}_t θtT 和 θ t S \boldsymbol{\theta}^{\mathcal{S}}_t θtS相等,继续训练。
- 只对一个模型进行提取。
2. DSA
方法就是在DC前面套了一层数据增强,可微的数据增强
进入正题,那么本文提出的DSA,可微暹罗增强(我也不知道为什么是暹罗)
2.1 暹罗增强
首先是暹罗增强,在图片数据中基本就是裁剪,旋转,颜色变换等
min S D ( ∇ θ L ( A ( S , ω S ) , θ t ) , ∇ θ L ( A ( T , ω T ) , θ t ) ) \min _{\mathcal{S}} D\left(\nabla_{\boldsymbol{\theta}} \mathcal{L}\left(\mathcal{A}\left(\mathcal{S}, \omega^{\mathcal{S}}\right), \boldsymbol{\theta}_t\right), \nabla_{\boldsymbol{\theta}} \mathcal{L}\left(\mathcal{A}\left(\mathcal{T}, \omega^{\mathcal{T}}\right), \boldsymbol{\theta}_t\right)\right) SminD(∇θL(A(S,ωS),θt),∇θL(A(T,ωT),θt))
此处 ω T \omega^{\mathcal{T}} ωT和 ω S \omega^{\mathcal{S}} ωS分别代表了在两个数据集上进行的数据增强参数。然后作者指出,如果使用随机分布的 ω T \omega^{\mathcal{T}} ωT和 ω S \omega^{\mathcal{S}} ωS会导致训练无法收敛,因此在文中使用的 ω T = ω S \omega^{\mathcal{T}} = \omega^{\mathcal{S}} ωT=ωS。
那么因为,浓缩数据集 S \mathcal{S} S和原始数据集 T \mathcal{T} T肯定是不一样的,那就没有一个一对一的关系,来进行同样的数据增强,那么文中的方法就是,一个batch的数据使用一样的数据增强。一个batch里 S \mathcal{S} S和 T \mathcal{T} T相互对应。
2.2 可微增强
要让这个过程可以BP训练,那么这个数据增强必须是可以微分的,即:
∂ D ( ⋅ ) ∂ S = ∂ D ( ⋅ ) ∂ ∇ θ L ( ⋅ ) ∂ ∇ θ L ( ⋅ ) ∂ A ( ⋅ ) ∂ A ( ⋅ ) ∂ S \frac{\partial D(\cdot)}{\partial \mathcal{S}}=\frac{\partial D(\cdot)}{\partial \nabla_{\boldsymbol{\theta}} \mathcal{L}(\cdot)} \frac{\partial \nabla_{\boldsymbol{\theta}} \mathcal{L}(\cdot)}{\partial \mathcal{A}(\cdot)} \frac{\partial \mathcal{A}(\cdot)}{\partial \mathcal{S}} ∂S∂D(⋅)=∂∇θL(⋅)∂D(⋅)∂A(⋅)∂∇θL(⋅)∂S∂A(⋅)

Traditionally transformations used for data augmentation are not implemented in a differentiable way, as optimizing input images is not their focus. Note that all the standard data augmentation methods for images are differentiable and can be implemented as differentiable layers.
这里是不是有点自相矛盾,传统数据增强变换实现不是可微的,但是图像上的标准数据增强方法是可微的?
2.3 训练过程

和DC基本一致,最外层训练K负责训练不同的模型初始化以增强浓缩数据集适用性,内层不断更新模型,训练T-1步,最内层是对每一个标签进行训练更新数据集。
3. 实验结果
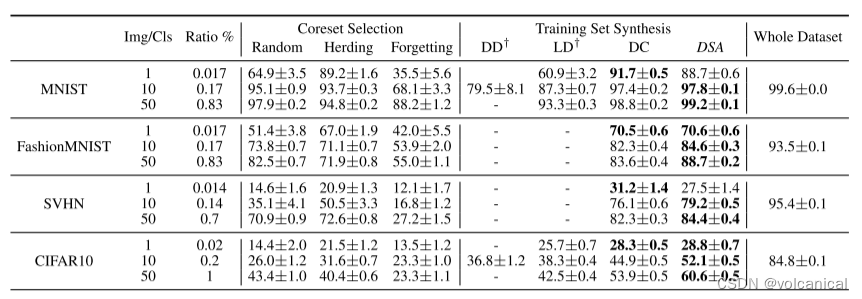
相关文章:

《Dataset Condensation with Differentiable Siamese Augmentation》
《Dataset Condensation with Differentiable Siamese Augmentation》 在本文中,我们专注于将大型训练集压缩成显著较小的合成集,这些合成集可以用于从头开始训练深度神经网络,性能下降最小。受最近的训练集合成方法的启发,我们提…...
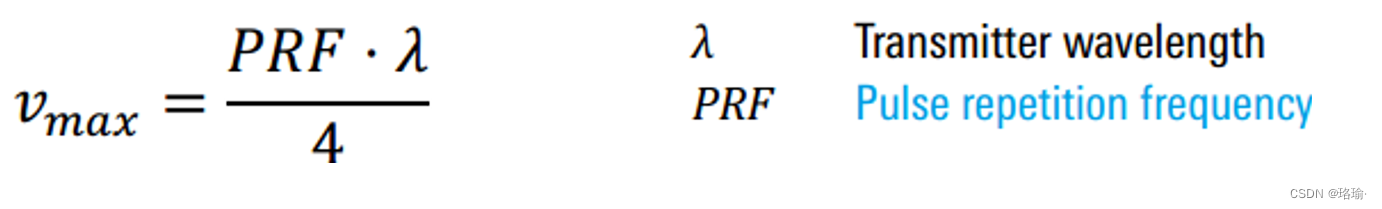
多普勒频率相关内容介绍
图1 多普勒效应 1、径向速度 径向速度是作用于雷达或远离雷达的速度的一部分。 图2 不同的速度 2、喷气发动机调制 JEM是涡轮机的压缩机叶片的旋转的多普勒频率。 3、多普勒困境 最大无模糊范围需要尽可能低的PRF; 最大无模糊速度需要尽可能高的PRF;…...
win10睡眠快捷方式
新建快捷方式 如下图 内容如下 rundll32.exe powrprof.dll,SetSuspendState 0,1,0 下一步 点击完成即可。 特此记录 anlog 2023年10月6日...

C++中的static和extern关键字
1 声明和定义 声明就是告诉编译器有这个东西的存在,而定义则是这个东西的实现。 对于变量来说,声明就是告诉编译器存在这个名称的变量,定义则是给这个变量分配内存并赋值: // 变量声明,声明时不能赋值,如…...

JAVA经典百题之找完数
题目:一个数如果恰好等于它的因子之和,这个数就称为"完数"。例如61+2+3.编程找出1000以内的所有完数。 程序分析 首先,我们需要编写一个程序来找出1000以内的所有完数。"完数"是指一个数等于它的…...

CSS 滚动驱动动画 view-timeline-inset
view-timeline-inset 语法例子🌰 正 scroll-padding 为正正的 length正的 percentage 负 scroll-padding 为负负的 length负的 percentage 兼容性 view-timeline-inset 在使用 view() 时说过, 元素在滚动容器的可见性推动了 view progress timeline 的进展. 默认…...

ansible部署二进制k8s
简介 GitHub地址: https://github.com/chunxingque/ansible_install_k8s 本脚本通过ansible来快速安装和管理二进制k8s集群;支持高可用k8s集群和单机k8s集群地部署;支持不同版本k8s集群部署,一般小版本的部署脚本基本是通用的。 …...
Nginx限流熔断
一、Nginx限流熔断 Nginx 是一款流行的反向代理和负载均衡服务器,也可以用于实现服务熔断和限流。通过使用 Nginx 的限流和熔断模块,比如:ngx_http_limit_req_module 和 ngx_http_limit_conn_module,可以在代理层面对服务进行限流…...

QQ登录的具体流程
文章目录 网站授权QQ登录QQ登录的完整流程代码示例1. 添加依赖2. 配置文件3. 实现Service4. 创建Controller 网站授权QQ登录 首先需要去QQ互联申请应用填写网站的相关信息,以及回调地址,需要进行审核。申请流程暂时不说了,百度一下挺多申请失…...
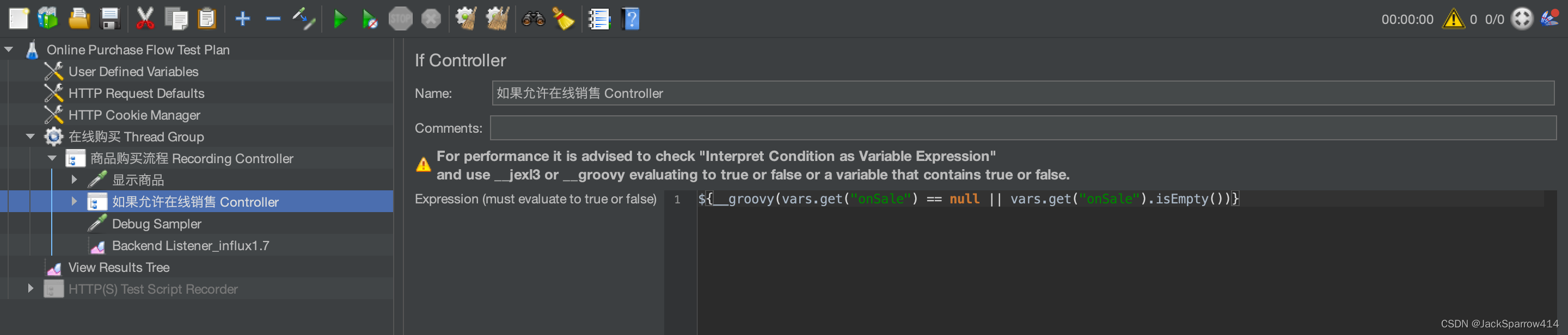
用JMeter对HTTP接口进行压测(一)压测脚本的书写、调试思路
文章目录 安装JMeter和Groovy为什么选择Groovy? 压测需求以及思路准备JMeter脚本以及脚本正确性验证使用Test Script Recorder来获取整条业务线上涉及的接口为什么使用Test Script Recorder? 配置Test Script Recorder对接口进行动态化处理处理全局变量以…...

接着聊聊如何从binlog文件恢复误delete的数据,模拟Oracle的闪回功能
看腻了文章就来听听视频演示吧:https://www.bilibili.com/video/BV1cV411A7iU/ delete忘加where条件(模拟Oracle闪回) 操作基本等同于上篇:再来谈谈如何从binlog文件恢复误update的数据,模拟Oracle的回滚功能 原理&a…...

计算机竞赛 深度学习机器视觉车道线识别与检测 -自动驾驶
文章目录 1 前言2 先上成果3 车道线4 问题抽象(建立模型)5 帧掩码(Frame Mask)6 车道检测的图像预处理7 图像阈值化8 霍夫线变换9 实现车道检测9.1 帧掩码创建9.2 图像预处理9.2.1 图像阈值化9.2.2 霍夫线变换 最后 1 前言 🔥 优质竞赛项目系列,今天要分…...

pyqt5使用经验总结
pyqt5环境配置注意: 安装pyqt5 pip install PyQt5 pyqt5-tools 环境变量-创建变量名: 健名:QT_QPA_PLATFORM_PLUGIN_PATH 值为:Lib\site-packages\PyQt5\Qt\plugins pyqt5经验2: 使用designer.exe进行设计࿱…...

【MQTT】mosquitto库中SSL/TLS相关API接口
文章目录 1.相关API1.1 mosquitto_tls_set1.2 mosquitto_tls_insecure_set1.3 mosquitto_tls_opts_set1.4 mosquitto_tls_insecure_set1.5 mosquitto_tls_set_context1.6 mosquitto_tls_psk_set 2.示例代码 Mosquitto 是一个流行的 MQTT 消息代理(broker)…...
假期题目整合
1. 下载解压题目查看即可 典型的猪圈密码只需要照着输入字符解开即可得到答案 2. 冷门类型的密码题型,需要特意去找相应的解题思路,直接百度搜索天干地支解密即可 3. 一眼能出思路他已经给了篱笆墙的提示提示你是栅栏密码对应解密即可 4. 最简单的社会主…...

Redisson—分布式服务
一、 分布式远程服务(Remote Service) 基于Redis的Java分布式远程服务,可以用来通过共享接口执行存在于另一个Redisson实例里的对象方法。换句话说就是通过Redis实现了Java的远程过程调用(RPC)。分布式远程服务基于可…...
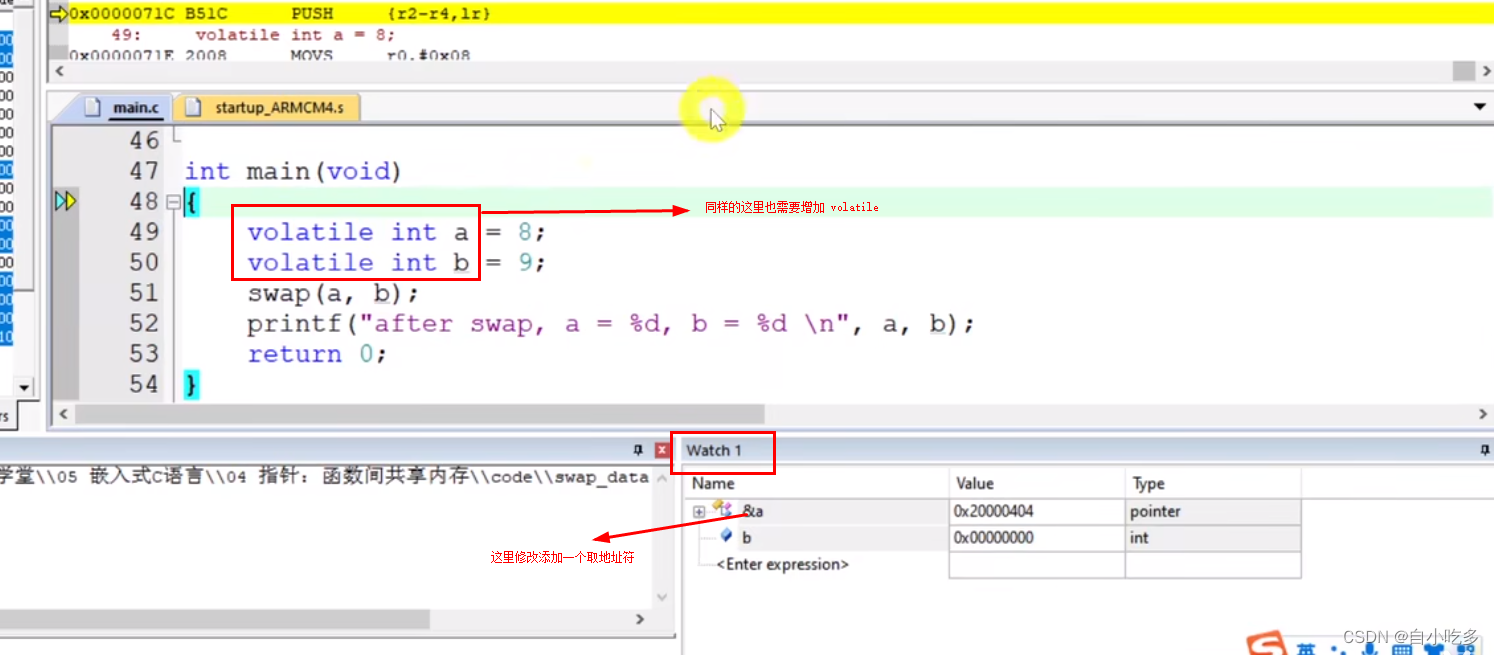
volatile使用方法
volatile使用方法 编译优化。使用等级3的话,可能将优化了一些变量。 这为什么会开启等第三呢?这是关于单片机的内存容量比较小,所以开启优化的话,可以可以省一些空间,但是如果。会出现些变量的问题,需要通过…...

提升您的 Go 应用性能的 6 种方法
优化您的 Go 应用程序 1. 如果您的应用程序在 Kubernetes 中运行,请自动设置 GOMAXPROCS 以匹配 Linux 容器的 CPU 配额 Go 调度器 可以具有与运行设备的核心数量一样多的线程。由于我们的应用程序在 Kubernetes 环境中的节点上运行,当我们的 Go 应用程…...
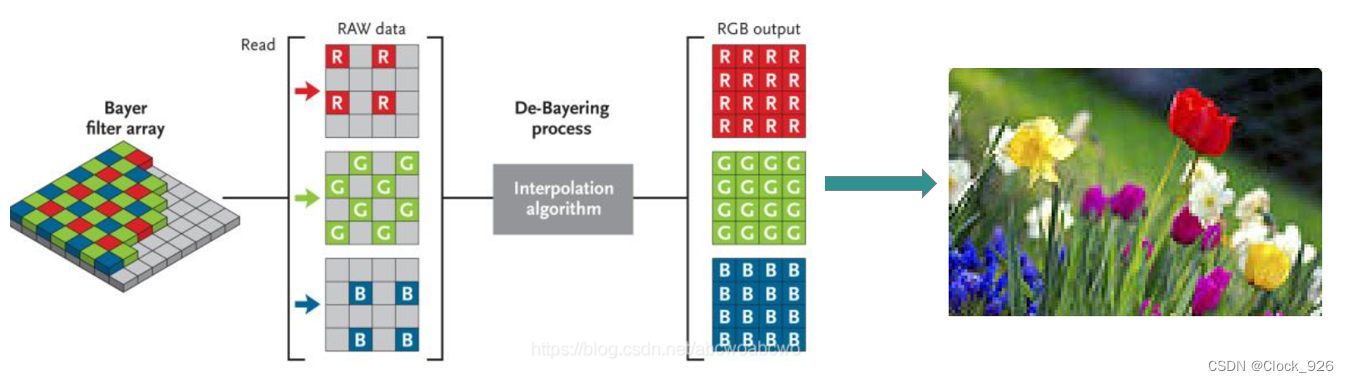
计算摄像技术02 - 颜色空间
一些计算摄像技术知识内容的整理:颜色视觉与感知特性、颜色空间和基于彩色滤镜阵列的彩色感知。 文章目录 一、颜色视觉与感知特性 (1)色调 (2)饱和度 (3)明度 二、颜色空间 (1&…...
Pytorch笔记之分类
文章目录 前言一、导入库二、数据处理三、构建模型四、迭代训练五、模型评估总结 前言 使用Pytorch进行MNIST分类,使用TensorDataset与DataLoader封装、加载本地数据集。 一、导入库 import numpy as np import torch from torch import nn, optim from torch.uti…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...
