python经典百题之一个素数能被几个9整除
题目:判断一个素数能被几个9整除。
首先,我们需要明确素数的定义:素数是大于1,且只能被1和自身整除的整数。
下面将分别介绍三种实现方法,每种方法附上解题思路、实现代码、以及优缺点。最后,将对这三种方法进行总结,并推荐其中更好的方法。
方法一: 逐步除以9
解题思路:
- 首先判断给定数是否为素数。
- 如果是素数,则从9开始逐步除以9,判断能够整除的次数。
实现代码:
def is_prime(num):if num < 2:return Falsefor i in range(2, int(num ** 0.5) + 1):if num % i == 0:return Falsereturn Truedef count_nines_divisible(num):if not is_prime(num):return 0count = 0while num % 9 == 0:count += 1num //= 9return count# 示例用法
num = 81
divisible_count = count_nines_divisible(num)
print(f"The prime number {num} can be divided by {divisible_count} nines.")
优缺点:
- 优点:
- 直接简单,易于理解和实现。
- 只需要判断能否被9整除,不需要预先生成素数列表。
- 缺点:
- 需要逐步除以9,可能需要多次除法运算。
方法二: 判断因子是否为9
解题思路:
- 首先判断给定数是否为素数。
- 如果是素数,则判断该素数是否只有因子9。
实现代码:
def is_prime(num):if num < 2:return Falsefor i in range(2, int(num ** 0.5) + 1):if num % i == 0:return Falsereturn Truedef is_nines_factor(num):if not is_prime(num):return Falsefactors = [i for i in range(2, num) if num % i == 0]return all(factor == 9 for factor in factors)# 示例用法
num = 81
is_nines = is_nines_factor(num)
print(f"The prime number {num} has all factors as nines: {is_nines}")
优缺点:
- 优点:
- 直接简单,易于理解和实现。
- 只需要判断因子是否为9,不需要预先生成素数列表。
- 缺点:
- 需要判断因子是否为9,可能需要多次判断。
方法三: 利用素数生成算法
解题思路:
- 使用素数生成算法生成素数列表。
- 对于每个素数,判断其能否被9整除。
实现代码:
def generate_primes(limit):primes = []is_prime = [True] * (limit + 1)is_prime[0] = is_prime[1] = Falsep = 2while p * p <= limit:if is_prime[p]:for i in range(p * p, limit + 1, p):is_prime[i] = Falsep += 1for i in range(2, limit + 1):if is_prime[i]:primes.append(i)return primesdef count_nines_divisible(primes):count = 0for prime in primes:if prime % 9 == 0:count += 1return count# 示例用法
limit = 100
primes = generate_primes(limit)
nines_divisible_count = count_nines_divisible(primes)
print(f"Count of primes that can be divided by 9: {nines_divisible_count}")
优缺点:
- 优点:
- 使用素数生成算法生成素数列表,降低了时间复杂度。
- 只需要判断能否被9整除,不需要逐步除以9。
- 缺点:
- 需要实现素数生成算法,稍复杂。
总结与推荐
-
总结:
- 方法一和方法二都是直接简单的实现,但可能需要多次除法运算或多次判断因子,效率不高。
- 方法三利用素数生成算法生成素数列表,避免了逐步除以9或多次判断因子,更高效。
-
推荐:
- 基于素数生成算法的方法(方法三)是相对更好的选择,因为它在时间上进行了较好的优化,并避免了逐步除以9或多次判断因子的操作。生成素数的过程虽然稍复杂,但可以节省时间成本,特别在处理大数字时更为高效。
相关文章:

python经典百题之一个素数能被几个9整除
题目:判断一个素数能被几个9整除。 首先,我们需要明确素数的定义:素数是大于1,且只能被1和自身整除的整数。 下面将分别介绍三种实现方法,每种方法附上解题思路、实现代码、以及优缺点。最后,将对这三种方法进行总结…...

Thymeleaf 内联语法使用教程
1 表达式内联 Thymeleaf标准方言允许使用标签属性(th:)来实现很多的功能,但在有些场景之下,需要将表达式直接写入HTML 代码中和CSS代码中及JavaScript代码中【代码和html文件在一起,分能不开,待验证,有验证的朋友可…...

Django学习笔记-实现聊天系统
笔记内容转载自 AcWing 的 Django 框架课讲义,课程链接:AcWing Django 框架课。 CONTENTS 1. 实现聊天系统前端界面2. 实现后端同步函数 1. 实现聊天系统前端界面 聊天系统整体可以分为两部分:输入框与历史记录。 我们需要先修改一下之前代…...
C++转换函数
什么是转换函数? C转换函数是一种特殊的成员函数,用于将一个类的对象转换为另一个类型。它是通过在类中定义特定的函数来实现的。 转换函数的用途: 类型转换:转换函数可以将一个类的对象从一种类型转换为另一种类型。这样可以方便地在不同…...

Spring Boot中的@Controller使用教程
一 Controller使用方法,如下所示: Controller是SpringBoot里最基本的组件,他的作用是把用户提交来的请求通过对URL的匹配,分配个不同的接收器,再进行处理,然后向用户返回结果。下面通过本文给大家介绍Spr…...
【17】c++设计模式——>原型模式
原型模式的定义 c中的原型模式(Prototype Pattern)是一种创建型设计模式,其目的是通过复制(克隆)已有对象来创建新的对象,而不需要显示的使用构造函数创建对象,原型模式适用于创建复杂对象时&a…...

金三银四好像消失了,IT行业何时复苏!
文章目录 1. 宏观经济形势2. 技术发展趋势3. 教育与培训4. 远程工作和自由职业5. 行业需求和公司招聘计划结论 🎉欢迎来到Java面试技巧专栏~金三银四好像消失了,IT行业何时复苏! ☆* o(≧▽≦)o *☆嗨~我是IT陈寒🍹✨博客主页&…...
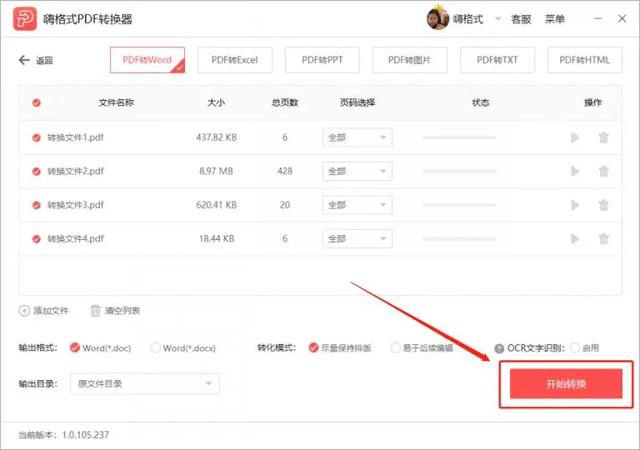
PDF文件超出上传大小?三分钟学会PDF压缩
PDF作为一种流行的文档格式,被广泛用于各种场合,然而有时候PDF文件的大小超出了上传限制,这时候我们就需要采取一些措施来减小PDF文件的大小,下面就给大家分享几个方法,一起来学习下吧~ 方法一:嗨格式压缩大…...

java入坑之国际化编程
一、字符编码 1.1概述 字符编码 --字符:0,a,我,①,,… --计算机只用0和1,1bit(0或者1) --ASCIL码(American Standard Code for Information Interchange) 美国信息交换标准代码,奠定计算机编码基础用一个字节(1Byte8b…...
Kafka客户端核心参数详解
这一部分主要是从客户端使用的角度来理解 Kakfa 的重要机制。重点依然是要建立自己脑海中的 Kafka 消费模型。Kafka 的 HighLevel API 使用是非常简单的,所以梳理模型时也要尽量简单化,主线清晰,细节慢慢扩展。 一、从基础的客户端说起 Kaf…...
踩大坑ssh免密登录详细讲解
目 录 问题背景 环境说明 免密登录流程说明 1.首先要在对应的用户主机名的情况下生成密钥对,在A服务器执行 2.将A服务器d公钥拷贝到B服务器对应的位置 3.在A服务器访问B服务器 免密登录流程 0.用户说明 1.目前现状演示 2.删除B服务器.ssh 文件夹下面的…...
操作系统八股
1、请你介绍一下死锁,产生的必要条件,产生的原因,怎么预防死锁 1、死锁 两个或两个以上的进程在执行过程中,因争夺共享资源而造成的一种互相等待的现象,若无外力作用,它们都将无法推进下去。此时称系统处…...

Hudi SQL DDL
本文介绍Hudi在 Spark 和 Flink 中使用SQL创建和更改表的支持。 1.Spark SQL 创建hudi表 1.1 创建非分区表 使用标准CREATE TABLE语法创建表,该语法支持分区和传递表属性。 CREATE TABLE [IF NOT EXISTS] [db_name.]table_name[(col_name data_type [COMMENT col_co…...
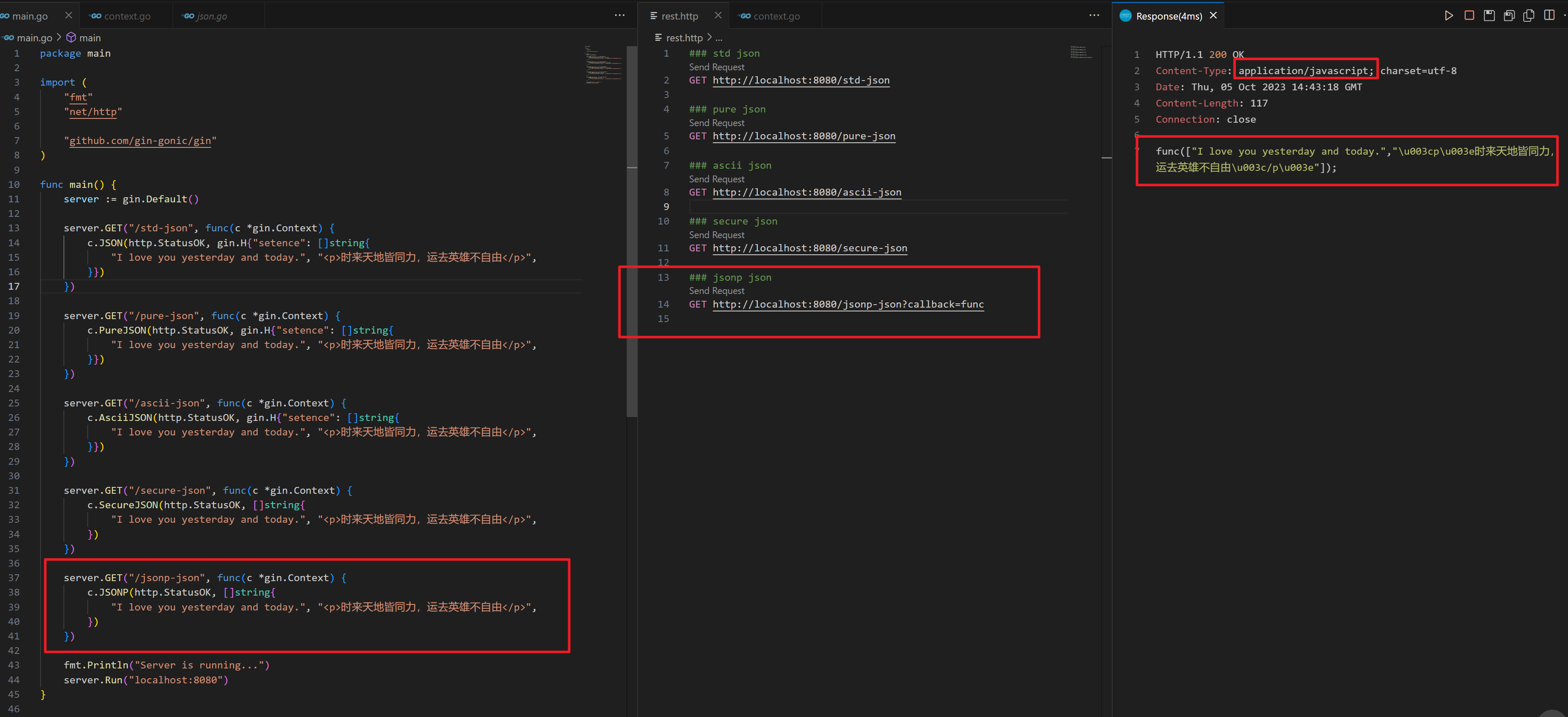
gin 框架的 JSON Render
gin 框架的 JSON Render gin 框架默认提供了很多的渲染器,开箱即用,非常方便,特别是开发 Restful 接口。不过它提供了好多种不同的 JSON Render,那么它们的区别是什么呢? // JSON contains the given interface obje…...
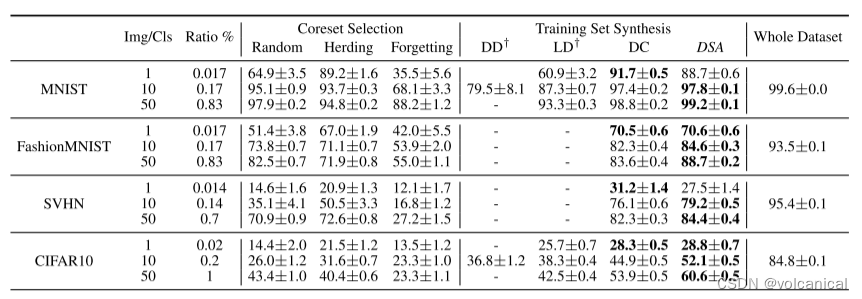
《Dataset Condensation with Differentiable Siamese Augmentation》
《Dataset Condensation with Differentiable Siamese Augmentation》 在本文中,我们专注于将大型训练集压缩成显著较小的合成集,这些合成集可以用于从头开始训练深度神经网络,性能下降最小。受最近的训练集合成方法的启发,我们提…...
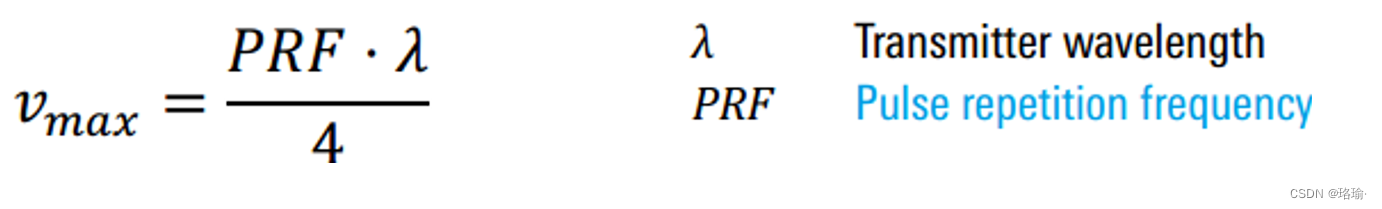
多普勒频率相关内容介绍
图1 多普勒效应 1、径向速度 径向速度是作用于雷达或远离雷达的速度的一部分。 图2 不同的速度 2、喷气发动机调制 JEM是涡轮机的压缩机叶片的旋转的多普勒频率。 3、多普勒困境 最大无模糊范围需要尽可能低的PRF; 最大无模糊速度需要尽可能高的PRF;…...
win10睡眠快捷方式
新建快捷方式 如下图 内容如下 rundll32.exe powrprof.dll,SetSuspendState 0,1,0 下一步 点击完成即可。 特此记录 anlog 2023年10月6日...

C++中的static和extern关键字
1 声明和定义 声明就是告诉编译器有这个东西的存在,而定义则是这个东西的实现。 对于变量来说,声明就是告诉编译器存在这个名称的变量,定义则是给这个变量分配内存并赋值: // 变量声明,声明时不能赋值,如…...

JAVA经典百题之找完数
题目:一个数如果恰好等于它的因子之和,这个数就称为"完数"。例如61+2+3.编程找出1000以内的所有完数。 程序分析 首先,我们需要编写一个程序来找出1000以内的所有完数。"完数"是指一个数等于它的…...

CSS 滚动驱动动画 view-timeline-inset
view-timeline-inset 语法例子🌰 正 scroll-padding 为正正的 length正的 percentage 负 scroll-padding 为负负的 length负的 percentage 兼容性 view-timeline-inset 在使用 view() 时说过, 元素在滚动容器的可见性推动了 view progress timeline 的进展. 默认…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...
