2023-2-10刷题情况
青蛙过河
题目描述
小青蛙住在一条河边, 它想到河对岸的学校去学习。小青蛙打算经过河里 的石头跳到对岸。
河里的石头排成了一条直线, 小青蛙每次跳跃必须落在一块石头或者岸上。 不过, 每块石头有一个高度, 每次小青蛙从一块石头起跳, 这块石头的高度就 会下降 1 , 当石头的高度下降到 0 时小青蛙不能再跳到这块石头上(某次跳跃 后使石头高度下降到 0 是允许的)。
小青蛙一共需要去学校上 x 天课, 所以它需要往返 2x 次。当小青蛙具有 一个跳跃能力 y 时, 它能跳不超过
y 的距离。
请问小青蛙的跳跃能力至少是多少才能用这些石头上完 x 次课。
输入格式
输入的第一行包含两个整数 n,x, 分别表示河的宽度和小青蛙需要去学校 的天数。请注意 2x 才是实际过河的次数。
第二行包含 n−1 个非负整数 1,2,⋯,H1,H2,⋯,Hn−11,2,⋯,H _1,H_2,⋯,H_n−11,2,⋯,H1,H2,⋯,Hn−1 , 其中 HiH_iHi 表示在河中与 小青蛙的家相距 i 的地方有一块高度为 HiH_iHi 的石头, HiH_iHi =0 表示这个位置没有石头。
输出格式
输出一行, 包含一个整数, 表示小青蛙需要的最低跳跃能力。
样例
样例输入
5 1
1 0 1 0
样例输出
4
样例说明
由于只有两块高度为 1 的石头,所以往返只能各用一块。第 1 块石头和对岸的距离为
4,如果小青蛙的跳跃能力为 3 则无法满足要求。所以小青蛙最少需要 4 的跳跃能力。
评测用例规模与约定
30% : n <= 100
50% : n <= 1000
100%:1<=n<=105,1<=x<=109,1<=HI<=1041 <= n <= 10^5, 1 <= x <= 10^9, 1 <= H_I <= 10^41<=n<=105,1<=x<=109,1<=HI<=104
运行限制
- 最大限制时间: 1s
- 最大空间限制:256MB
思路
尽量大的里面选最小,很有可能是要使用二分(做题做出来的规律),能够跳跃的长度即为区间长度,能够跳过当前区间的条件是,当前区间的石头的长度和大于等于2x,区间长度在枚举的过程中需要逐步递增,且当前区间的石头总和在递增,这便有了单调性,然后就是在满足条件后,取最小值。
代码实现
import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改public class Main {static int n, k;static int[] arr;public static void main(String[] args) {Scanner sc = new Scanner(System.in);//在此输入您的代码...n = sc.nextInt();k = sc.nextInt();arr = new int[n];for(int i = 1; i < n; i++){arr[i] = arr[i-1] + sc.nextInt();}int l = 0, r = n+1;while(l < r){int mid = (l + r) >> 1;if(judge(mid)) r = mid;else l = mid + 1;}System.out.println(l);sc.close();}private static boolean judge(int x){int min = Integer.MAX_VALUE;for(int i = 1; i + x <= n; i++){min = Math.min(min, arr[i+x-1] - arr[i-1]);}if(min >= 2 * k) return true;return false;}
}
在排序数组中查找元素的第一个和最后一个位置
题目描述
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
样例
样例输入
nums = [5,7,7,8,8,10], target = 8
nums = [5,7,7,8,8,10], target = 6
nums = [], target = 0
样例输出
[3,4]
[-1,-1]
[-1,-1]
提示
- 0<=nums.length<=1050 <= nums.length <= 10^50<=nums.length<=105
- −109<=nums[i]<=109-10^9 <= nums[i] <= 10^9−109<=nums[i]<=109
- nums是一个非递减数组nums 是一个非递减数组nums是一个非递减数组
- −109<=target<=109-10^9 <= target <= 10^9−109<=target<=109
思路
标准二分咯,今天就是做完上一题后,感觉自己的二分还不够熟练,今天特地练习一下。
代码实现
class Solution {public int[] searchRange(int[] nums, int target) {if(nums.length == 0) return new int[]{-1, -1};int[] ans = new int[2];int l = 0, r = nums.length;// 左闭右开区间,当nums[mid]= target时,r = mid, 也是一直在缩小区间范围。// 单一个开区间,开右区间好点,开左区间mid似乎得向上取整。// 这个二分的结果为第一个出现target的位置。while(l < r){int mid = (l + r) / 2;if(nums[mid] < target) l = mid + 1;else r = mid;}if(l == nums.length || nums[l] != target) return new int[]{-1, -1};ans[0] = (nums[l] == target ? l : -1);l = 0;r = nums.length - 1;// 左闭右闭区间,这样子容易求的第一个出现target和最后一个出现target的位置。// 改改if的条件技能修改结果为第一个出现target的位置或最后一个出现target的位置。while(l <= r){int mid = (l + r) / 2;if(nums[mid] > target) r = mid - 1;else l = mid + 1;}/* 左闭由开区间,但是mid得向上取整,即(left+right+1)/ 2;求的是最后一个出现target的位置。while(l < r){int mid = (l + r + 1) / 2;if(nums[mid] > target) r = mid - 1;else l = mid;}*/ans[1] = (nums[r] == target ? r : -1);return ans;}
}
掷骰子模拟
题目描述
有一个骰子模拟器会每次投掷的时候生成一个 1 到 6 的随机数。
不过我们在使用它时有个约束,就是使得投掷骰子时,连续 掷出数字 i 的次数不能超过 rollMax[i](i 从 1 开始编号)。
现在,给你一个整数数组 rollMax 和一个整数 n,请你来计算掷 n 次骰子可得到的不同点数序列的数量。
假如两个序列中至少存在一个元素不同,就认为这两个序列是不同的。由于答案可能很大,所以请返回 模 10^9 + 7 之后的结果。
样例
样例输入
n = 2, rollMax = [1,1,2,2,2,3]
n = 2, rollMax = [1,1,1,1,1,1]
n = 3, rollMax = [1,1,1,2,2,3]
样例输出
34
我们掷 2 次骰子,如果没有约束的话,共有 6 * 6 = 36 种可能的组合。但是根据 rollMax 数组,数字 1 和 2 最多连续出现一次,所以不会出现序列 (1,1) 和 (2,2)。因此,最终答案是 36-2 = 34。
30
181
提示
- 1 <= n <= 5000
- rollMax.length == 6
- 1 <= rollMax[i] <= 15
思路
最优结果肯定为动态规划,但是,动态规划的转移转移方程式并不是很容易就想出来的。借此题使得如何将算法优化至动态规划。
代码实现
暴力递归模拟,递归程序中有几个需要关注的信息,上一个点数,持续了几个次,当前投掷了几个骰子。
暴力递归模拟,时间复杂度属于指数级,还是很容易超时的。
class Solution {private static final int MOD = (int)1e9+7;int[] rollMax;public int dieSimulator(int n, int[] rollMax) {int max = Arrays.stream(rollMax).max().getAsInt();this.rollMax = rollMax;cache = new int[n][6][max];for(int i = 0; i < n; i++)for(int j = 0; j < 6; j++)Arrays.fill(cache[i][j], -1);long res = 0;for(int i = 0; i < 6; i++){res += dfs(n-1, i, rollMax[i]-1);}return (int)(res % MOD);}private int dfs(int i, int last, int left){if(i == 0) return 1;long res = 0;for(int k = 0; k < 6; k++){if(k != last) res += dfs(i-1, k, rollMax[k]-1);else if(left > 0) res += dfs(i-1, k, left-1);}return (int)(res % MOD);}
}
记忆化搜索,将已经计算过的结果记录下来,下次遇到同等情况,直接返回记录的结果即可。
将已经计算的结果记录下来,能过很大程度的降低时间复杂度。
class Solution {private static final int MOD = (int)1e9+7;int[] rollMax;int[][][] cache;public int dieSimulator(int n, int[] rollMax) {int max = Arrays.stream(rollMax).max().getAsInt();this.rollMax = rollMax;cache = new int[n][6][max];for(int i = 0; i < n; i++)for(int j = 0; j < 6; j++)Arrays.fill(cache[i][j], -1);long res = 0;for(int i = 0; i < 6; i++){res += dfs(n-1, i, rollMax[i]-1);}return (int)(res % MOD);}private int dfs(int i, int last, int left){if(i == 0) return 1;if(cache[i][last][left] != -1) return cache[i][last][left];long res = 0;for(int k = 0; k < 6; k++){if(k != last) res += dfs(i-1, k, rollMax[k]-1);else if(left > 0) res += dfs(i-1, k, left-1);}return cache[i][last][left] = (int)(res % MOD);}
}
动态规划
记忆化的递归即是自上向下的执行程序,其实在递归的时候,状态转移方程式,就已经写在递归函数中了。
只需将自上向下的程序修改为自下向上,就是动态规划。
class Solution {private static final int MOD = (int)1e9+7;public int dieSimulator(int n, int[] rollMax){int len = rollMax.length;int max = Arrays.stream(rollMax).max().getAsInt();var dp = new long[n][6][max];for(int i = 0; i < 6; i++)Arrays.fill(dp[0][i], 1);for(int i = 1; i < n; i++){for(int last = 0; last < 6; last++){for(int left = 0; left < max; left++){long res = 0;for(int j = 0; j < len; j++){if(j != last) res += dp[i-1][j][rollMax[j]-1];else if(left > 0) res += dp[i-1][j][left-1];}dp[i][last][left] = res % MOD;}}}long ans = 0;for(int i = 0; i < 6; i++) ans += dp[n-1][i][rollMax[i]-1];return (int)(ans % MOD);}
}
相关文章:

2023-2-10刷题情况
青蛙过河 题目描述 小青蛙住在一条河边, 它想到河对岸的学校去学习。小青蛙打算经过河里 的石头跳到对岸。 河里的石头排成了一条直线, 小青蛙每次跳跃必须落在一块石头或者岸上。 不过, 每块石头有一个高度, 每次小青蛙从一块石头起跳, 这块石头的高度就 会下降 1 , 当石头…...

Python学习-----无序序列2.0(集合的创建、添加、删除以及运算)
目录 前言: 什么是集合 集合的三大特性 1.集合的创建 (1)直接创建 (2)强制转换 2.集合的添加 (1)add()函数 (2)update() 函数 3.集合元…...

2023最详细的接口测试用例设计教程
一、接口测试流程 1、需求讨论 2、需求评审 3、场景设计 4、数据准备 5、测试执行 二、分析接口文档元素 1、接口名称 2、接口地址 3、支持格式 4、请求方式 5、请求参数(参数名称、类型、是否必填、参数说明等) 6、返回参数(返回…...
【数据库】 数据库的理论基础详解
目录 一, 什么是数据库 二, 数据库管理系统(DBMS) 三,数据库与文件系统的区别 1,对比区别: 2,优缺点总结: 四,数据库的发展史 五,常见数据库 1, 关系型…...
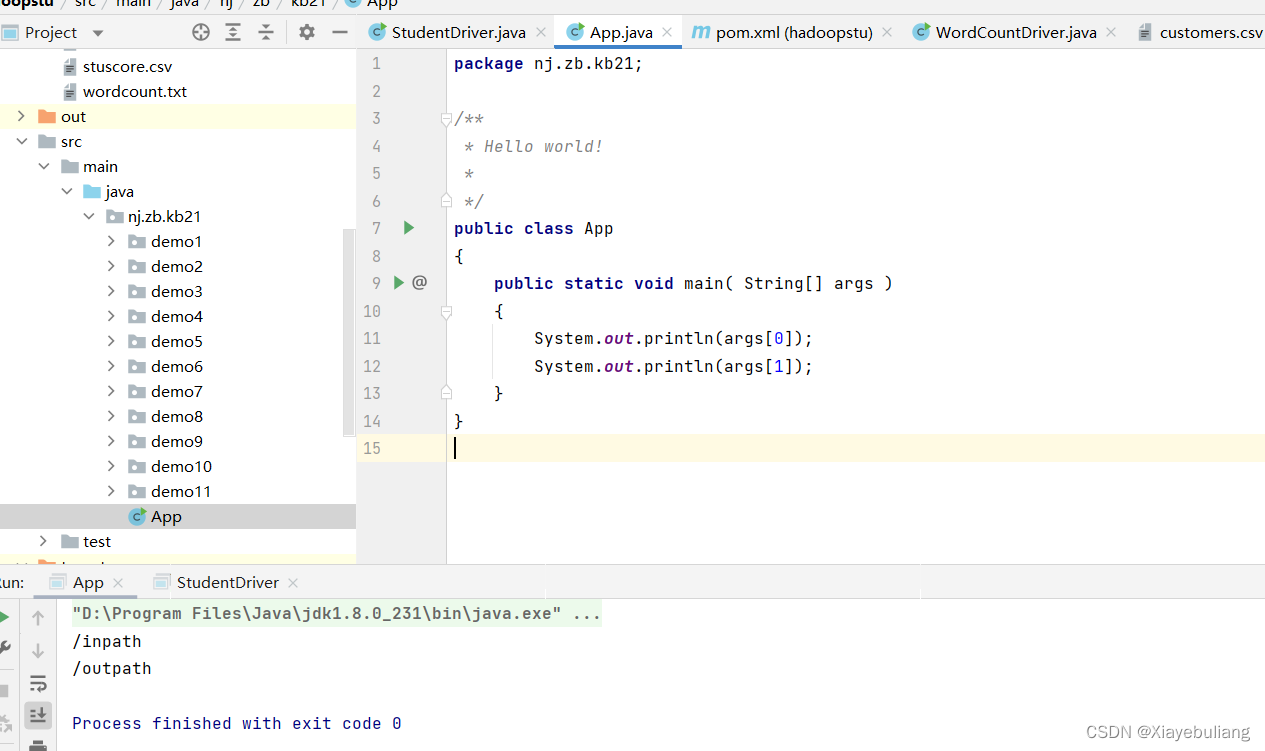
Linux环境运行Maven 生成的hadoop jar包
运行命令: hadoop jar ./jar包名字 class对象路径 输入路径 输出路径 linux内部jar包测试 cd 到以下目录,创建以下文件夹 [rootreagan180 ~]# cd /opt/soft/hadoop313/share/hadoop/mapreduce/ 创建文件夹(读取路径) [roo…...
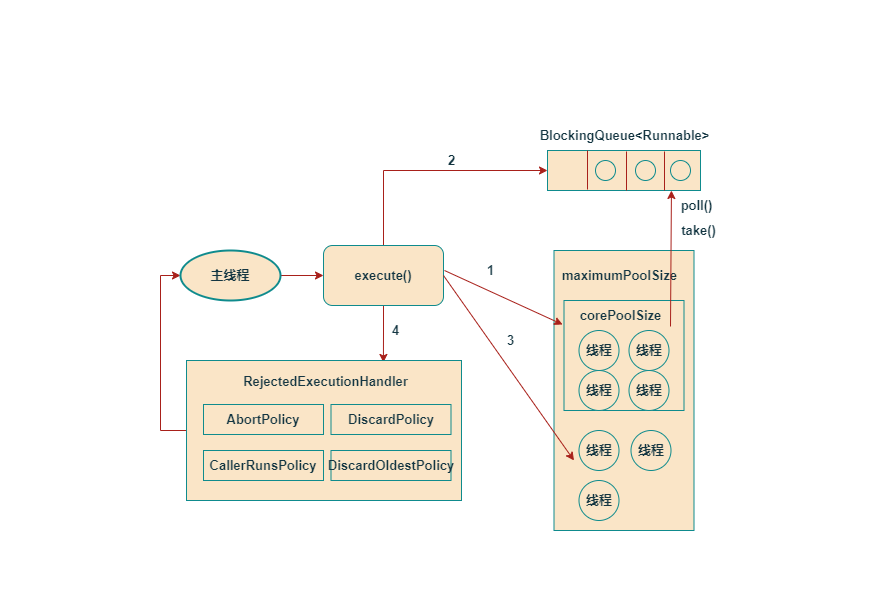
ThreadPoolExecutor原理解析
1. 工作原理1.1 流程图1.2 执行示意图从上图得知如果当前运行的线程数小于corePoolSize(核心线程数),则会创建新线程作为核心线程来执行任务(注意,执行这一步需要获取全局锁)。如果运行的线程等于或多于corePoolSize,则将任务加入BlockingQue…...

谷粒学苑第二章前端框架-2.2前端框架开发过程
一、前端框架开发过程 第一步:添加路由 src/router模块用来管理路由。 第二步:点击某个路由,显示路由对应页面内容 component: () > import(/views/table/index), 表示路由对应的页面,是views/table/index.vue页面 第三步&a…...
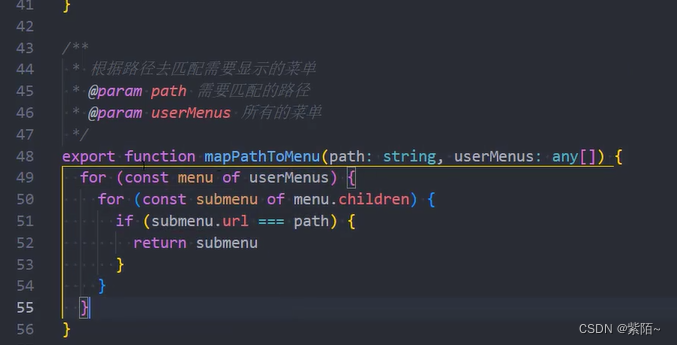
权限管理实现的两种方式(详解)
登录的接口请求的三个内容:1. token2. 用户信息、角色信息3. 菜单信息第一种:基于角色Role的动态路由管理 (不推荐,但市场用的比较多)首先列出枚举每个角色对应几个路由,然后根据用户登录的角色遍历枚举出来的角色动态注册对应的路…...

【C++】智能指针思路解析和模拟实现
此篇文章就从以下几个方面出发,带你了解智能指针的方方面面1.为什么需要智能指针当我们开辟内存并使用的时候,我们的顺序应该是这样:开辟内存-》使用内存-》释放内存问题就出现在第三步,开辟好了,也使用了,…...
:Sentinel流控降级入门)
SpringCloud(18):Sentinel流控降级入门
Sentinel本地应用流控降级实现分为三步: 创建本地应用搭建本地Sentinel控制台本地应用接入本地Sentinel控制台1 本地应用创建 整体流程分析 创建springboot项目在项目的pom.xml文件中引入sentinel-core的依赖坐标创建TestController,定义使用限流规则运行测试具体流程 1.创…...
C++【多态】
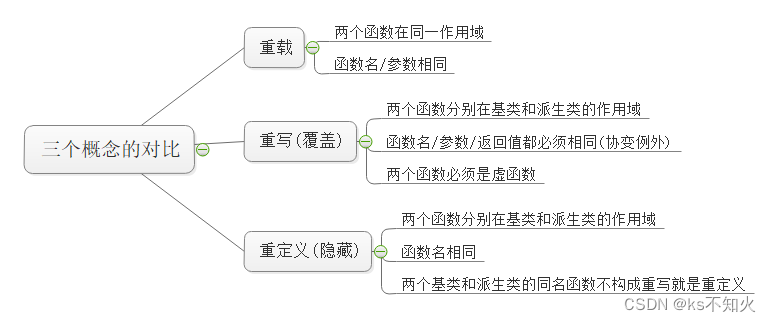
文章目录1、多态的概念2、多态的定义及实现2-1、多态的构成条件2-2、虚函数2-3、虚函数的重写2-4 多态样例2-5、协变2-6、 析构函数与virtual2-7、函数重载、函数隐藏(重定义)与虚函数重写(覆盖)的对比2-8、override 和 final&…...

缓存预热、缓存雪崩、缓存击穿、缓存穿透,你真的了解吗?
缓存穿透、缓存击穿、缓存雪崩有什么区别,该如何解决? 1.缓存预热 1.1 问题描述 请求数量较高,大量的请求过来之后都需要去从缓存中获取数据,但是缓存中又没有,此时从数据库中查找数据然后将数据再存入缓存…...
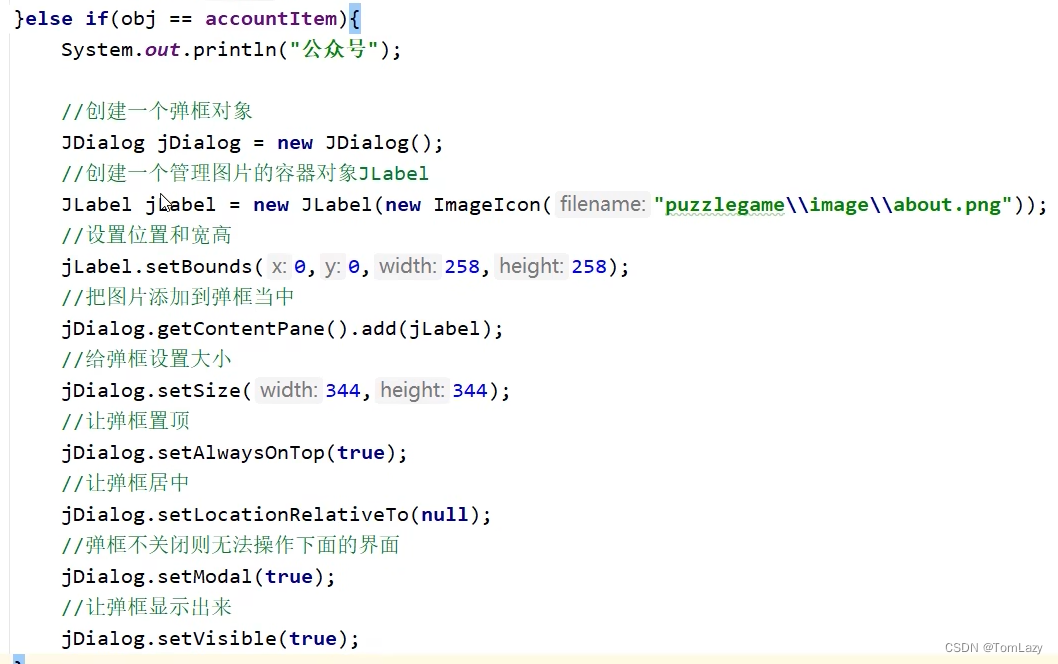
【Java基础】018 -- 面向对象阶段项目上(拼图小游戏)
目录 拼图小游戏(GUI) 一、主界面分析 1、练习一:创建主界面1 2、练习二:创建主界面2(JFrame) 3、练习三:在游戏界面中添加菜单(JMenuBar) ①、菜单的制作 4、添加图片&a…...
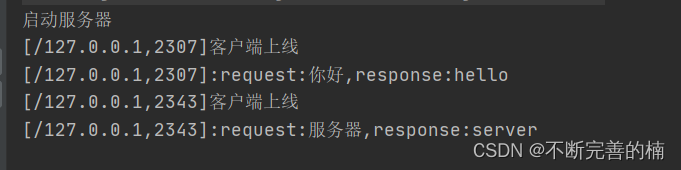
【网络~】
网络一级目录二、socket套接字三、UDP数据报套接字四、TCP流套接字一级目录 1.局域网、广域网 2.IP地址是什么? IP地址是标识主机在网络上的地址 IP地址是如何组成的? 点分十进制,将32位分为四个部分,每个部分一个字节ÿ…...

手写JavaScript中的call、bind、apply方法
手写JavaScript中的call、bind、apply方法 call方法 call() 方法使用一个指定的 this 值和单独给出的一个或多个参数来调用一个函数。 function Product(name, price) {this.name name;this.price price; }function Food(name, price) {Product.call(this, name, price);t…...

JAVA练习46-将有序数组转换为二叉搜索树
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 前言 提示:这里可以添加本文要记录的大概内容: 2月10日练习内容 提示:以下是本篇文章正文内容,下面案例可供参考 一、题目-…...
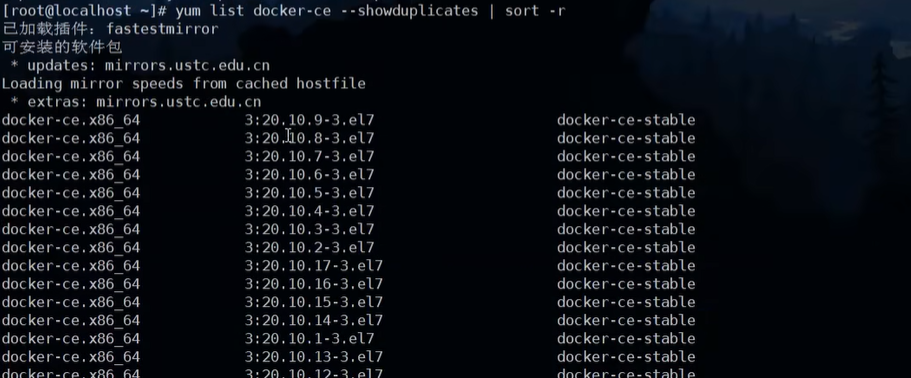
linux(centos7.6)docker
官方文档:https://docs.docker.com/engine/install/centos/1安装之前删除旧版本的docker2安装yum install-y yum-utils3配置yum源 不用官网的外国下载太慢 推荐阿里云yum-config-manager --add-repo https://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.r…...

微信小程序滚动穿透问题
文章目录1、catchtouchmove"true"2、page-meta3、wx.setPageStyle做小程序的开发业务中,经常会使用弹窗,当弹窗里的内容过多时,要滚动查看,然后经常会遇到滚动弹窗,弹窗底下页面也跟着滚。解决思路ÿ…...
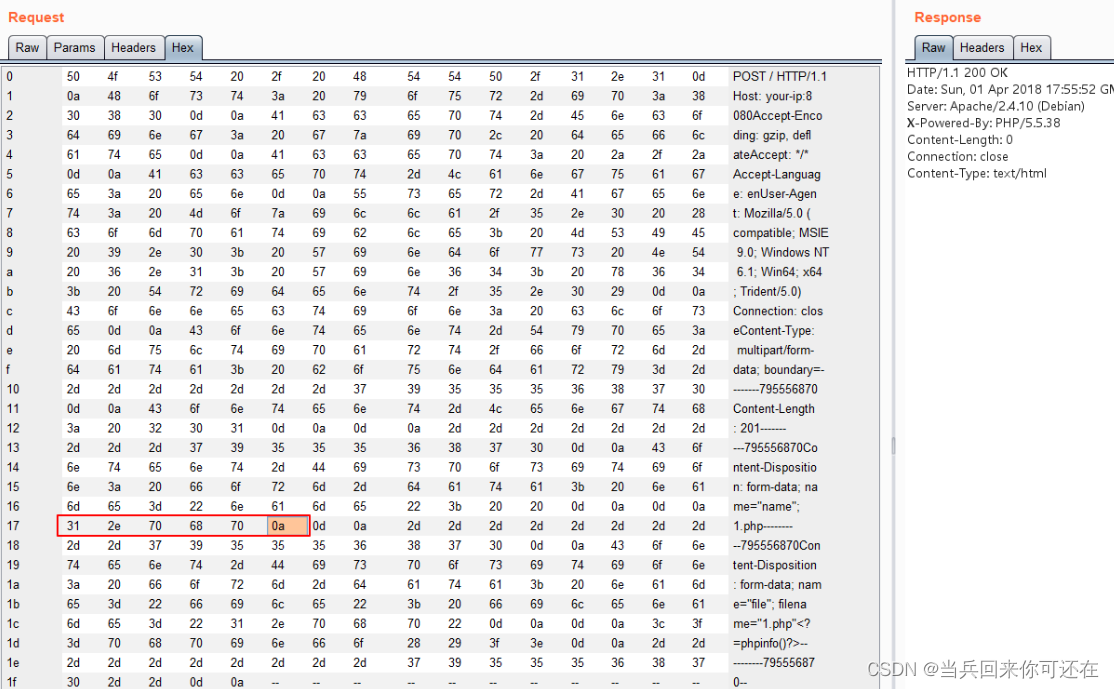
安全—06day
负载均衡反向代理下的webshell上传负载均衡负载均衡下webshell上传的四大难点难点一:需要在每一台节点的相同位置上传相同内容的webshell难点二:无法预测下一次请求是哪一台机器去执行难点三:当我们需要上传一些工具时,麻烦来了&a…...

PostgreSQL入门
PostgreSQL入门 简介 PostgreSQL是以加州大学伯克利分校计算机系开发的POSTGRES, 版本 4.2为基础的对象关系型数据库管理系统(ORDBMS) 支持大部分SQL标准并且提供了许多现代特性 复杂查询外键触发器可更新视图事务完整性多版本并发控制 …...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...
