OpenRadar DOA函数 Bartlett/CBF和Capon使用
Bartlett / CBF原理看这里
Capon原理看这里
这里只讲怎么调用openradar提供的aoa_bartlett和aoa_capon函数:
一些吐槽:虽然看起来openradar的作者代码水平很高,但里面有很多匪夷所思的写法,比如他demo里的解析文件格式就很迷啊等等…
先获取矢量矩阵 (steering vector):
比如果你想得到[-90°,90°],分辨率为1°(就有181个角度点),8根虚拟天线的矢量矩阵,那么就会生成一个shape为[181, 8]的ndarray (也就是下面那行代码的steering_vec)。num_vec得到的是一共有多少角度(上面那个例子的话就是181),没啥用,可以不管。
num_vec, steering_vec = dsp.gen_steering_vec(ANGLE_RANGE, ANGLE_RES, VIRT_ANT)
By the way, dsp.gen_steering_vec里面用了np.complex, 高版本的numpy可能不支持,报错说和python自带的complex有歧义,把np去掉,变成complex即可。
ANGLE_RANGE 是在一侧,你要得到多少角度信息,那么一共就有 2 * ANGLE_RANGE + 1个角度信息,+1是因为0°。
ANGLE_RES 是你需要的角度分辨率
VIRT_ANT 是虚拟天线数
以下举例
ANGLE_RANGE = 90
ANGLE_RES = 1
VIRT_ANT = 8
BINS_PROCESSED = 112
意思想得到的角度为[-90°, 90°],因为有0,所以有2*ANGLE_RANGE + 1 = 181个角度格子,想要的角度分辨率为1°,处理前112个range-bin。
Bartlett/CBF:
radar_cube shape : (128, 8, 128) - (chirp, vx, adc_samples)
ra = np.zeros((ANGLE_BINS, BINS_PROCESSED), dtype=np.complex128)
# 只取前BIN_PROCESSED个range-bin处理
ra = dsp.aoa_bartlett(steering_vec, radar_cube[:, :, :BINS_PROCESSED], axis=1)
ra = ra.sum(0) # 对所有chirp的得到的角度信息求和
plt.title('bartlet sum all chirps')
plt.imshow(np.abs(ra))
下面我尝试跟着Bartlett的原理自己写了一个函数,实测效果一致。
只取了第一个chirp,没像上面那样求和,实测这两种方法差不多,对所有chirp得到的角度信息求和(上面那种)的话效果会好一点点点点点。
radar_cube2 shape : (8, 128) - (vx, adc_samples)
ra = np.zeros((ANGLE_BINS, BINS_PROCESSED), dtype=np.complex128)
steering_vec = np.conjugate(steering_vec) # 要取共轭!
for i in range(BINS_PROCESSED): # 遍历每一个range-bin,得到每个range-bin上的角度信息tmp = steering_vec @ radar_cube2[:, i]ra[:, i] = tmp
plt.title('CBF conjugate')
# openradar bartlett源码就是把得到的每个角度的复数取模然后再平方,这样写是对的,我对比过用dsp.aoa_bartlett的range-angle图,效果一样
plt.imshow(np.abs(ra) ** 2)
Capon
radar_cube shape : (128, 8, 256) - (chirps, vx, adc_samples)
range_azimuth = np.zeros((ANGLE_BINS, BINS_PROCESSED), dtype=np.complex128)
for i in range(BINS_PROCESSED):range_azimuth[:, i], beamWeights[:,i] = dsp.aoa_capon(radar_cube[:, :, i].T, steering_vec, magnitude=False)
plt.title('256 chirps Capon')
plt.imshow(np.abs(range_azimuth))
此外,如果你的chirp小于8,比如1个frame里只有1个chirp,那么就要把openradar的dsp.angle_estimation.cov_matrix里的这个判断删了:
if x.shape[0] > x.shape[1]:warnings.warn("cov_matrix input should have Vrx as rows. Needs to be transposed", RuntimeWarning)x = x.T
大概意思就是他觉得你输错了,还帮你改正了,但实际上你没输错,他帮了倒忙,就是要处理一帧里面,1个chirp,8根虚拟天线的数据,anyway,如果一帧里只有小于虚拟天线个数的chirp数的话,把这段判断删了或注释掉就行。
下面的视频是我对这Bartlett/CBF和Capon和Angle-FFT在openradar的circle.bin这个数据上的效果对比:
相关文章:

OpenRadar DOA函数 Bartlett/CBF和Capon使用
Bartlett / CBF原理看这里 Capon原理看这里 这里只讲怎么调用openradar提供的aoa_bartlett和aoa_capon函数: 一些吐槽:虽然看起来openradar的作者代码水平很高,但里面有很多匪夷所思的写法,比如他demo里的解析文件格式就很迷啊等…...
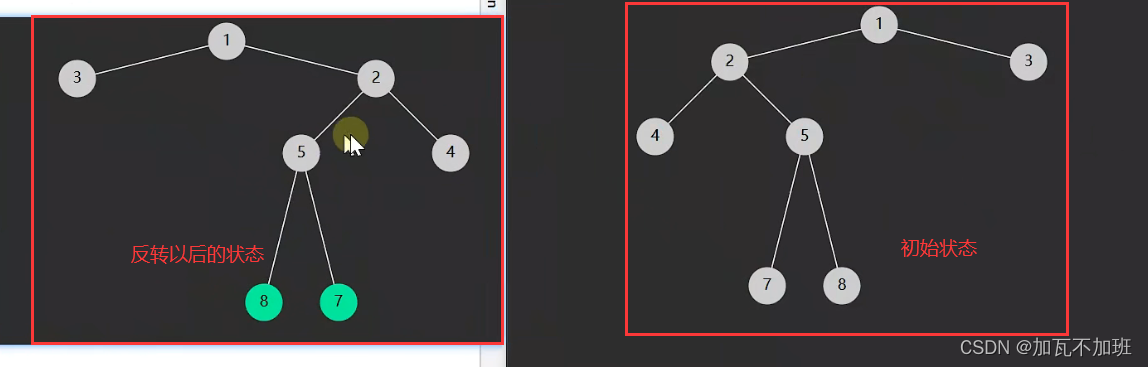
二叉树--翻转二叉树
文章前言:如果有小白同学还是对于二叉树不太清楚,作者推荐:二叉树的初步认识_加瓦不加班的博客-CSDN博客 给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。 如果思路不清楚,请看动态页面&am…...
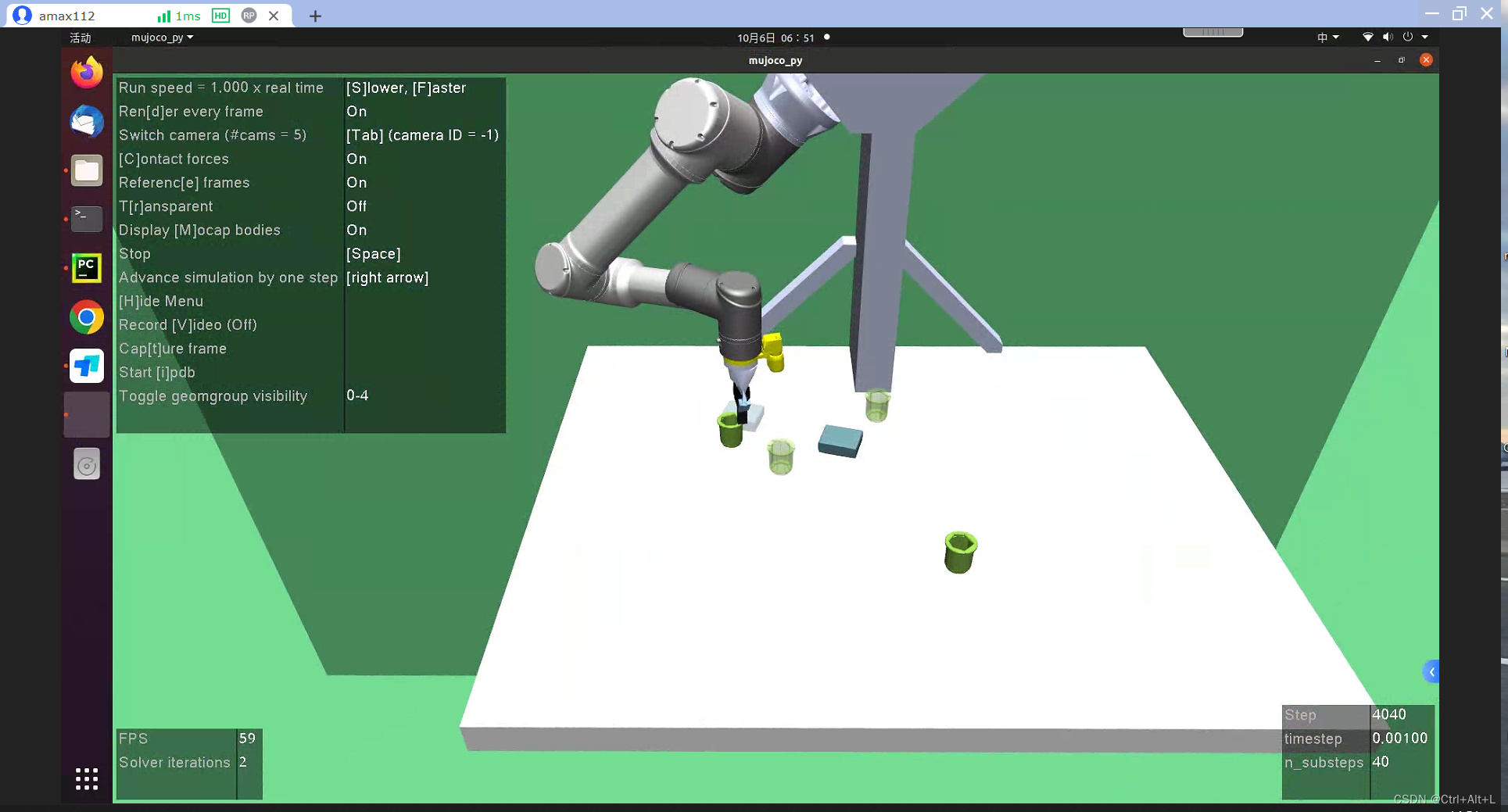
强化学习环境 - robogym - 学习 - 3
强化学习环境 - robogym - 学习 - 3 文章目录 强化学习环境 - robogym - 学习 - 3项目地址为什么选择 robogymObservation - 观测信息Action - 动作信息Initialization - 初始状态设置 项目地址 https://github.com/openai/robogym 为什么选择 robogym 自己的项目需要做一些机…...
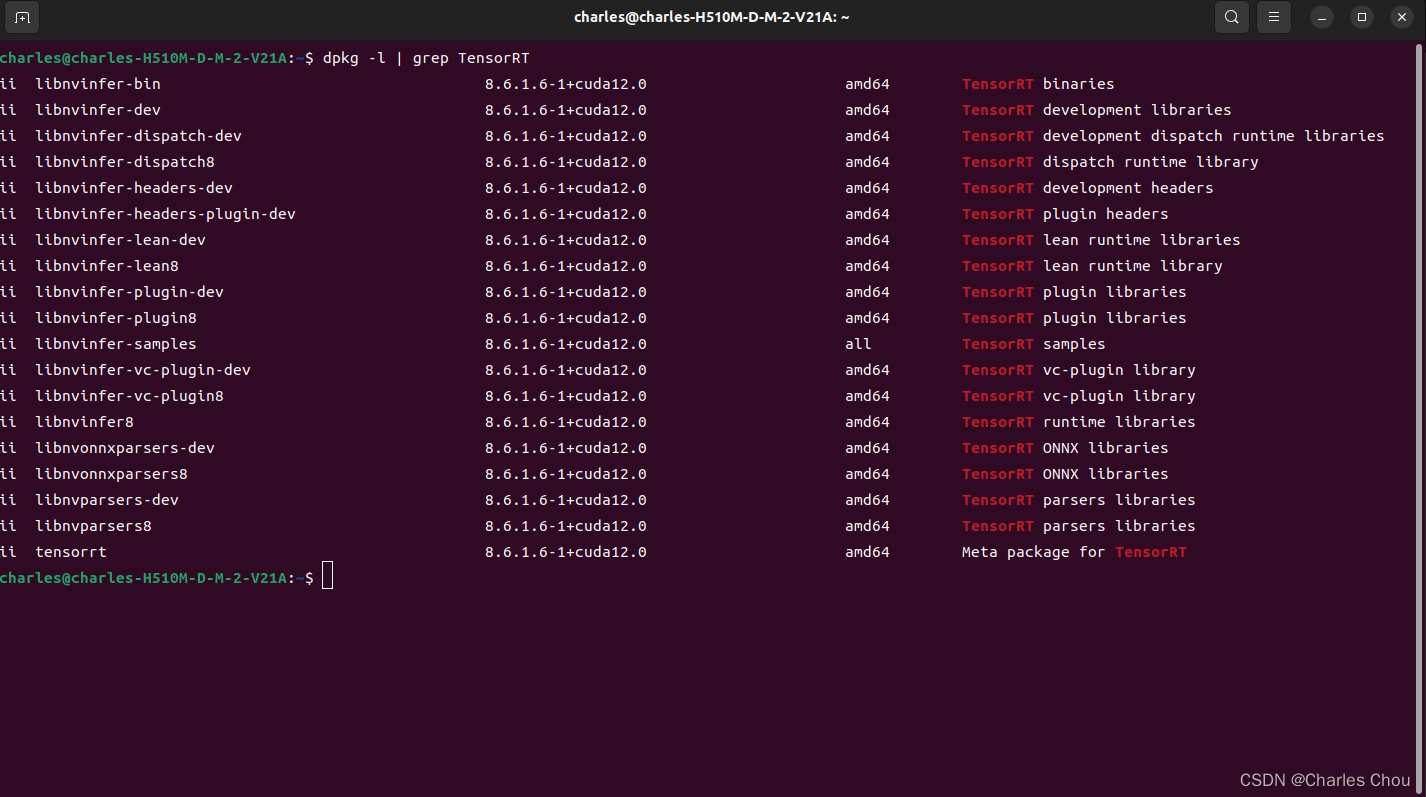
CUDA+cuDNN+TensorRT 配置避坑指南
深度学习模型加速部署的环境配置,需要在本地安装NVIDIA的一些工具链和软件包,这是一个些许繁琐的过程,而且一步错,步步错。笔者将会根据自己的经验来提供建议,减少踩坑几率。当然可以完全按照官方教程操作,…...
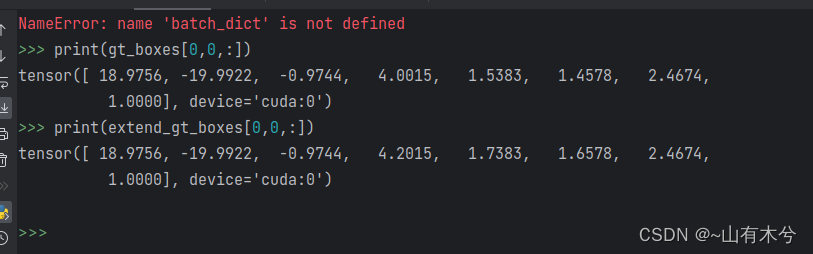
关于PointHeadBox类的理解
forward函数 def forward(self, batch_dict):"""Args:batch_dict:batch_size:point_features: (N1 N2 N3 ..., C) or (B, N, C)point_features_before_fusion: (N1 N2 N3 ..., C)point_coords: (N1 N2 N3 ..., 4) [bs_idx, x, y, z]point_labels (opti…...
ajax的使用)
javascript二维数组(10)ajax的使用
在JQuery中,使用AJAX的方法主要有以下几种: $.ajax():这是JQuery中最通用的AJAX请求方法。它需要一个包含各种参数的对象,其中包括请求的URL、请求方式、数据类型、请求参数等。请求成功后执行的回调函数也是通过参数来定义的。 …...

CMMI5认证哪些企业可以申请
CMMI5认证哪些企业可以申请 什么是CMMI5认证 CMMI(Capability Maturity Model Integration)是一种用于评估组织的软件工程能力的国际标准。CMMI模型包括5个等级,其中CMMI5是最高等级,代表组织具有达到持续优化和创新的能力。获得…...
【iptables 实战】9 docker网络原理分析
在开始本章阅读之前,需要提前了解以下的知识 阅读本节需要一些docker的基础知识,最好是在linux上安装好docker环境。提前掌握iptables的基础知识,前文参考【iptables 实战】 一、docker网络模型 docker网络模型如下图所示 说明࿱…...
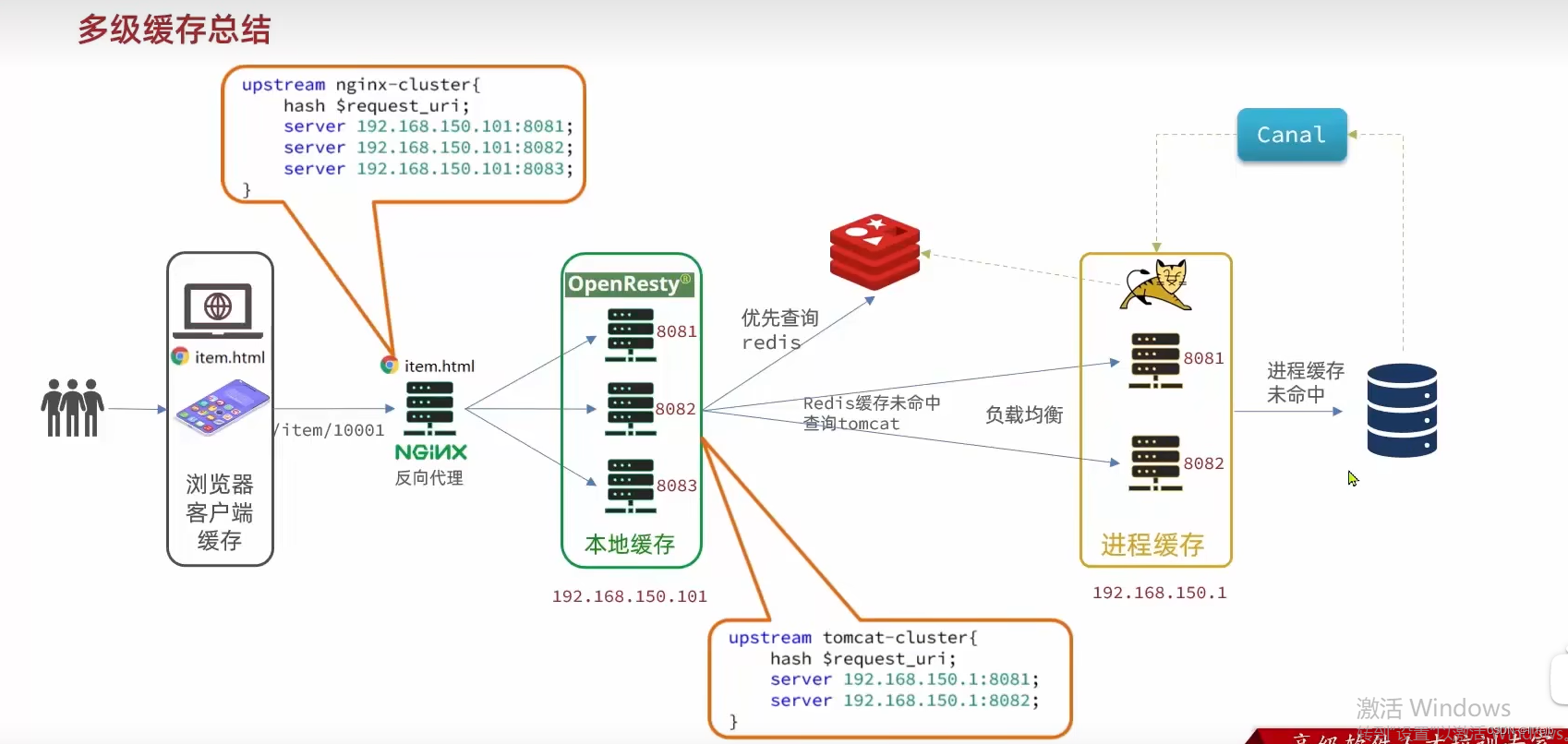
【多级缓存】
文章目录 1. JVM进程缓存2. Lua语法3. 实现多级缓存3.1 反向代理流程3.2 OpenResty快速入门 4. 查询Tomcat4.1 发送http请求的API4.2 封装http工具4.3 基于ID负载均衡4.4 流程小结 5. Redis缓存查询5.1 实现Redis查询 6. Nginx本地缓存6.1 本地缓存API6.2 实现本地缓存查询 7. …...
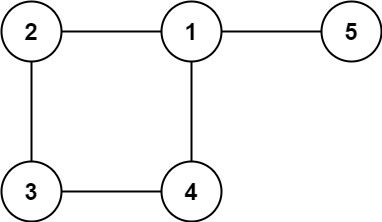
第五课 树与图
文章目录 第五课 树与图lc94.二叉树的中序遍历--简单题目描述代码展示 lc589.N叉树的层序遍历--中等题目描述代码展示 lc297.二叉树的序列化和反序列化--困难题目描述代码展示 lc105.从前序与中序遍历序列构造二叉树--中等题目描述代码展示 lc106.从中序与后序遍历序列构造二叉…...

2023-10-07 事业-代号z-副业-CQ私服-调研与分析
摘要: CQ作为一款运营了20年的游戏, 流传出的私服可以说是层出不穷, 到了现在我其实对这款游戏的长线运营的前景很悲观. 但是作为商业的一部分, 对其做谨慎的分析还是很有必要的. 传奇调研的来源: 一. 各种售卖私服的网站 传奇服务端版本库-传奇手游源码「免费下载」传奇GM论…...
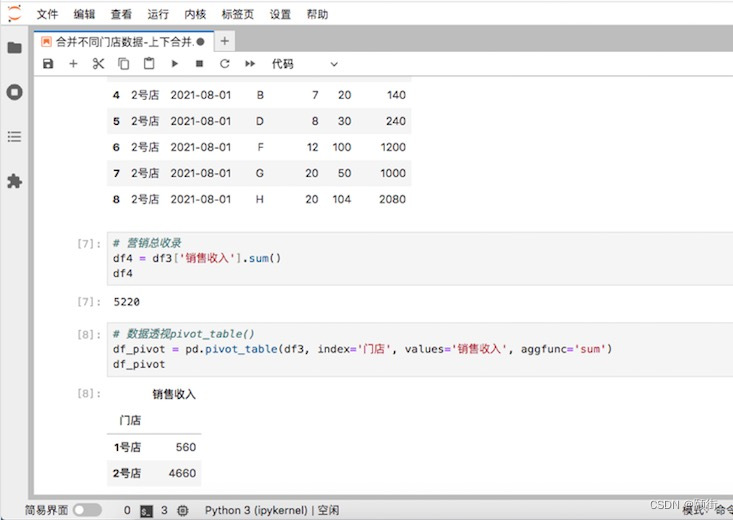
合并不同门店数据-上下合并
项目背景:线下超市分店,统计产品的销售数量和销售额,并用透视表计算求和 merge()函数可以根据链接键横向连接两张不同表,concat()函数可以上下合并和左右合并2种不同的合并方式。merge()函数只能横向连接两张表,而con…...

学习记忆——数学篇——案例——算术——整除特点
理解记忆法 对于数的整除特征大家都比较熟悉:比如4看后两位(因为100是4的倍数),8看后三位(因为1000是8的倍数),5末尾是0或5,3与9看各位数字和等等,今天重点研究一下3,9,…...

PHP8中的魔术方法-PHP8知识详解
在PHP 8中,魔术方法是一种特殊的方法,它们以两个下划线(__)开头。魔术方法允许您定义类的行为,例如创建对象、调用其他方法或访问和修改类的属性。以下是一些常见的魔术方法: __construct(): 类的构造函数…...

[图论]哈尔滨工业大学(哈工大 HIT)学习笔记23-31
视频来源:4.1.1 背景_哔哩哔哩_bilibili 目录 1. 哈密顿图 1.1. 背景 1.2. 哈氏图 2. 邻接矩阵/邻接表 3. 关联矩阵 3.1. 定义 4. 带权图 1. 哈密顿图 1.1. 背景 (1)以地球为建模,从一个大城市开始遍历其他大城市并且返回…...

Nginx+Keepalived实现服务高可用
Nginx 和 Keepalived 是常用于构建高可用性(High Availability)架构的工具。Nginx 是一款高性能的Web服务器和反向代理服务器,而Keepalived则提供了对Nginx服务的健康状态监测和故障切换功能。 下载Nginx 在服务器1和服务器2分别下载nginx …...
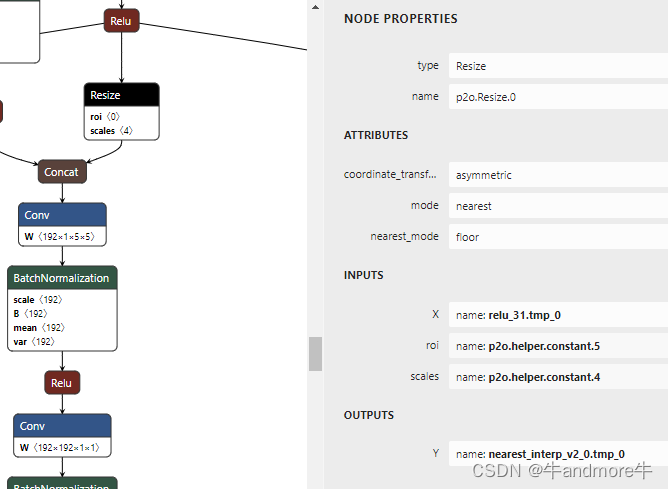
picodet onnx转其它芯片支持格式时遇到
文章目录 报错信息解决方法两模型精度对比 报错信息 报错信息为: Upsample(resize) Resize_0 not support attribute coordinate_transformation_mode:half_pixel. 解决方法 整个模型转换过程是:paddle 动态模型转成静态,再用paddle2onnx…...

【学习笔记】CF704B Ant Man
智商不够啊,咋想到贪心的😅 非常经典的贪心模型🤔 首先,从小到大将每个 i i i插入到排列中,用 D P DP DP记录还有多少个位置可以插入,可以通过钦定新插入的位置左右两边是否继续插入数来提前计算贡献。注…...

SQLines数据迁移工具
Data and Analytics Platform Migration - SQLines Tools SQLines提供的工具可以帮助您在不同的数据库平台之间传输数据、转换数据库模式(DDL)、视图、存储过程、包、用户定义函数(udf)、触发器、SQL查询和SQL脚本。 SQLines SQL Converter OverviewCommand LineConfigurati…...
)
pkl文件与打开(使用numpy和pickle)
文章目录 1. 什么是pkl文件2. 如何打开?Reference 1. 什么是pkl文件 1)python中有一种存储方式,可以存储为.pkl文件。 2)该存储方式,可以将python项目过程中用到的一些暂时变量、或者需要提取、暂存的字符串、列表、…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...
