课题学习(三)----倾角和方位角的动态测量方法(基于陀螺仪的测量系统)
一、内容介绍
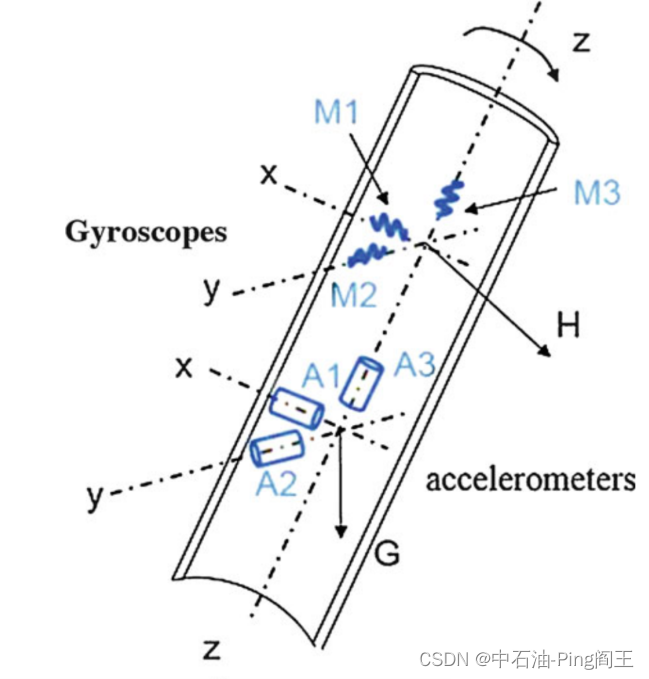
该测量系统基于三轴加速度和三轴陀螺仪,安装在钻柱内部,随钻柱一起旋转,形成捷联惯性导航系统,安装如下图所示:
假设三轴加速度和陀螺仪的输出为: f b = [ f x f y f z ] T f^b=\begin{bmatrix}f_{x} & f_{y} &f_{z} \end{bmatrix}^T fb=[fxfyfz]T w b = [ w x w y w z ] T w^b=\begin{bmatrix}w_{x} & w_{y} &w_{z} \end{bmatrix}^T wb=[wxwywz]T
使用这六轴的输出可以非常有效的求解姿态,应用惯性导航的求解算法,可以实现钻孔时的连续测量。加速度计和陀螺仪可以在坐标系中提供线加速度和角速度。但是,如果要求解钻具的位姿,则需要将该坐标系转换为另一个坐标系。
Xe、Ye、Ze三个轴代表地球坐标系。导航坐标系用于计算载体的位置、速度和姿态,因为导航坐标系沿当地的北、东、垂直方向,如下图中的“N, E, UP”,其中λ为经度角,φ为纬度角。在载体坐标系下,利用INS力学方程可得到井斜、井向和工具面角。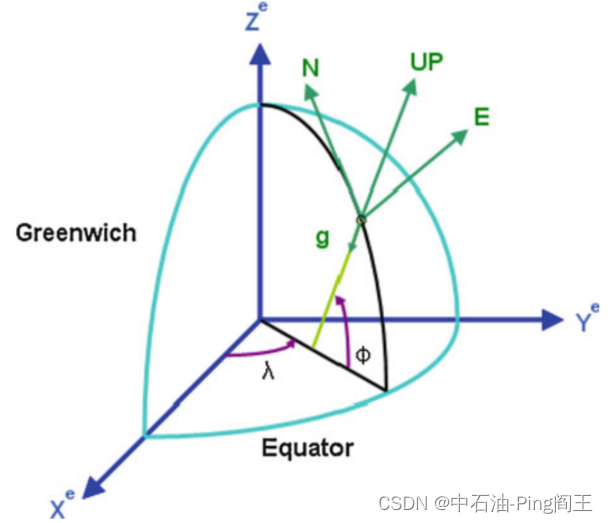
将b系统中测得的加速度和角速度值通过变换矩阵Rn b转换为n系统,即可求解井底工具的空间位置和姿态[28]。定义底部的经度为λ,纬度为φ,海拔为h,则其位置可表示为: r n = [ φ λ h ] T r^n=\begin{bmatrix}φ & λ &h \end{bmatrix}^T rn=[φλh]T
定义n系统的速度分量,向北速度为Vn,向东速度为Ve,垂直速度为Vu。然后定义n系统的速度为: r n = [ V e V n V u ] T r^n=\begin{bmatrix}V^e & V^n &V^u\end{bmatrix}^T rn=[VeVnVu]T
速度分量可以表示为位置分量对时间的导数:
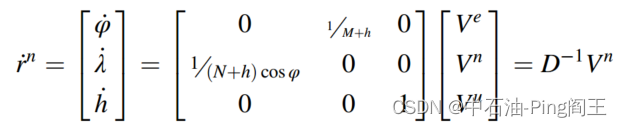
上式中,M为子午线的曲率半径,N为地球椭圆的曲率半径。
在载体坐标系下,加速度计 f b = [ f x f y f z ] T f^b=\begin{bmatrix}f_{x} & f_{y} &f_{z}\end{bmatrix}^T fb=[fxfyfz]T 通过变换矩阵 R b n R^n_{b} Rbn转换到地理坐标系的测量值为:

n坐标系中的加速度分量 f n f^n fn可以对速度分量 v n v^n vn积分。但由于地球本身的存在,会影响求解过程。地球自转速度为 w e = 15 d e g / h r w^e=15deg/hr we=15deg/hr,用n坐标系表示的角速度矢量如下式所示:
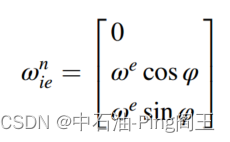
地理坐标系的变化取决于导航坐标系中北方和垂直方向的定义。北方方向通常指向子午线方向,垂直方向指向地球表面,如下图所示: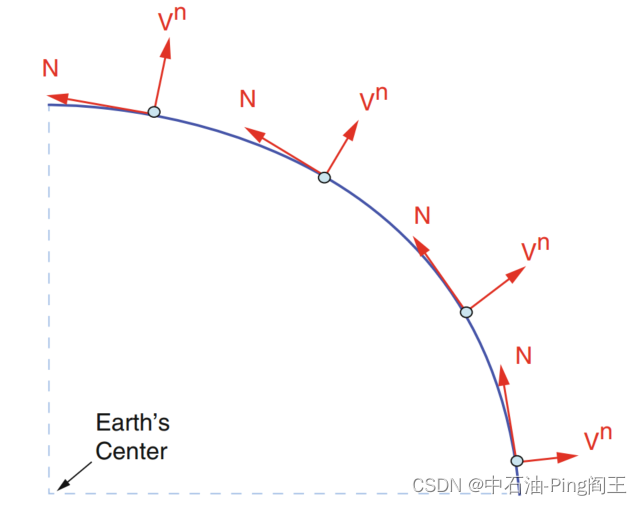
在导航坐标系中,角速度矢量可表示为:
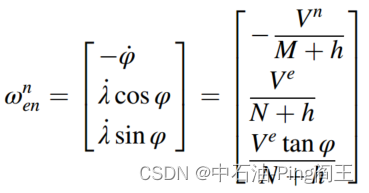
地球引力也影响IMU的加速度测量。我们可以用重力模型来修正。地球重力场可以表示为: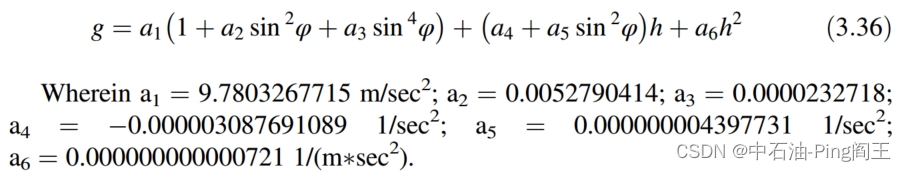
地球引力场在n系列中可以表示为: g n = [ 0 0 − g ] g^n=\begin{bmatrix}0&0&-g\end{bmatrix} gn=[00−g].考虑到地球因素的影响,速度分量Vn的变化率可以表示为: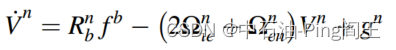
其中:
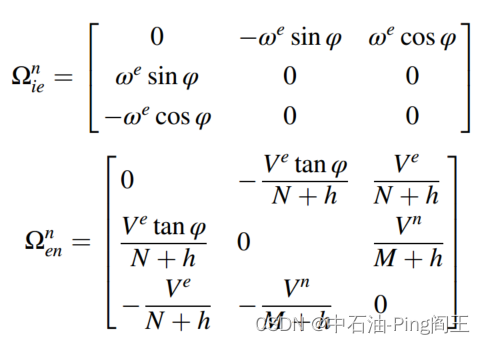
变换矩阵 R b n R^n_{b} Rbn可由以下微分方程得到:
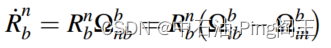
其中 Ω i b b Ω^b_{ib} Ωibb为陀螺仪测得的角速度的反对称矩阵,角速度矢量 Ω i b b Ω^b_{ib} Ωibb可表示为:
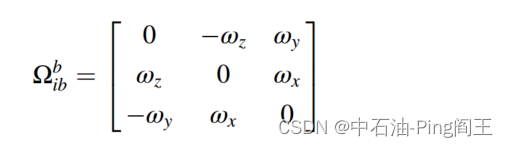
陀螺仪测量底部钻具的角速度,同时也测量地球自转的角速度和导航坐标系的方向。因此,需要从 Ω i b b Ω^b_{ib} Ωibb中减去角速度 Ω i n b Ω^b_{in} Ωinb,以消除这两个因素的影响。角速度矢量 Ω i n b Ω^b_{in} Ωinb包含两部分,第一部分是地球自转速度 Ω i e b Ω^b_{ie} Ωieb和导航坐标系方向变化速度 Ω e n b Ω^b_{en} Ωenb,如下图所示: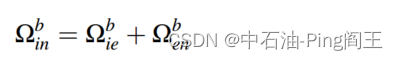
速度矩阵的反对称矩阵可以表示为: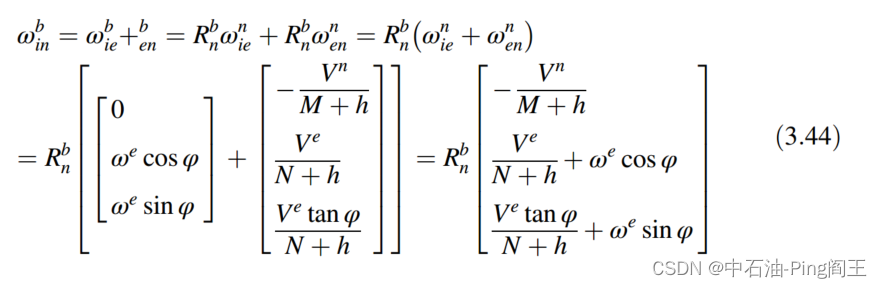
最后得到变换矩阵如下: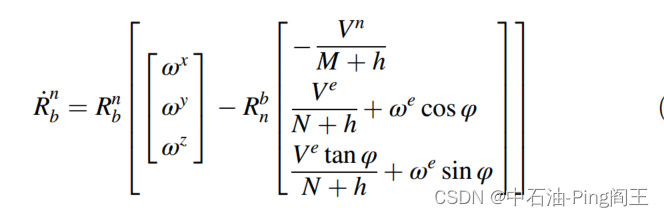
定义井斜角为θ,方位角为ψ,工具面为φ,变换矩阵 R b n R^n_{b} Rbn可表示为: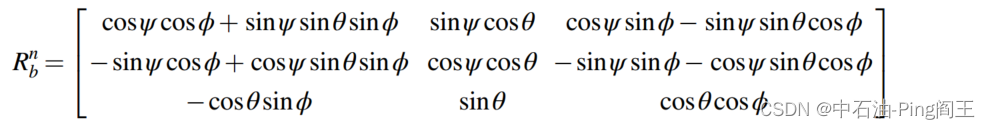
根据前面的假设,三轴加速度计的输出信号为: f b = [ f x f y f z ] T f^b=\begin{bmatrix}f_{x} & f_{y} &f_{z} \end{bmatrix}^T fb=[fxfyfz]T 三轴陀螺仪的输出信号为: w b = [ w x w y w z ] T w^b=\begin{bmatrix}w_{x} & w_{y} &w_{z} \end{bmatrix}^T wb=[wxwywz]T 从测量的角速度可以计算出角度变化量:

同样,由加速度的测量值可以计算出线速度: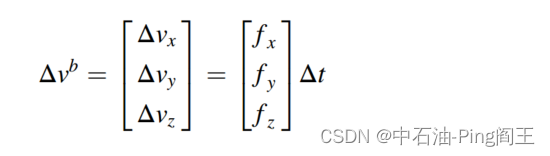
考虑到地球自转和导航坐标系方向变化的影响,在时刻tk时,角度的增加可表示为: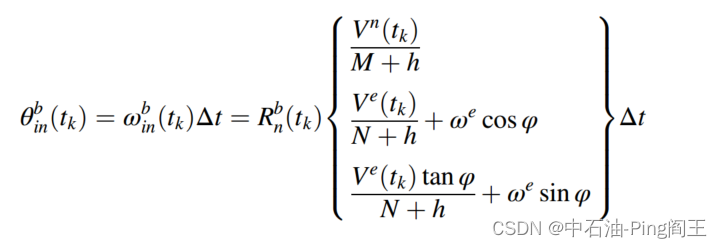
然后,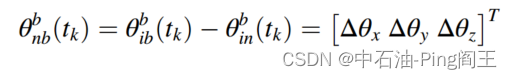
综上所述,基于地理坐标系的捷联惯性导航系统的力学方程如下:
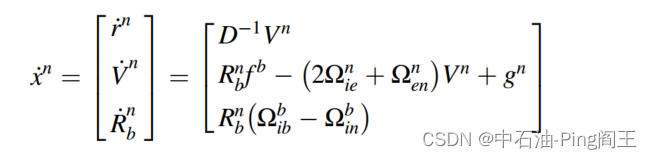
上式的解可以用欧拉角法、方向余弦法或四元数法求解。通过在载体轴上安装三轴加速度计和三轴陀螺仪,可以通过测量值获得载体的姿态、速度和位置等信息。
二、往期回顾
课题学习(一)----静态测量
课题学习(二)----倾角和方位角的动态测量方法(基于磁场的测量系统)
相关文章:
课题学习(三)----倾角和方位角的动态测量方法(基于陀螺仪的测量系统)
一、内容介绍 该测量系统基于三轴加速度和三轴陀螺仪,安装在钻柱内部,随钻柱一起旋转,形成捷联惯性导航系统,安装如下图所示: 假设三轴加速度和陀螺仪的输出为: f b [ f x f y f z ] T f^b\begin{bmatrix}f_{x} …...

1876. 长度为三且各字符不同的子字符串
1876. 长度为三且各字符不同的子字符串 C代码:滑动窗口 // 存在三种字符,且不重复、子串数量 int countGoodSubstrings(char * s){int k 3;int hash[26] {0};int len 0;int l 0;int ans 0;for (int i 0; i < strlen(s); i) {hash[s[i] - a];if…...
Mall脚手架总结(一)——SpringSecurity实现鉴权认证
前言 在结束理论知识的学习后,荔枝开始项目学习,这个系列文章将围绕荔枝学习mall项目过程中总结的知识点来梳理。本篇文章主要涉及如何整合Spring Security和JWT实现鉴权认证的功能!希望能帮助到一起学习mall项目的小伙伴~~~ 文章目录 前言 …...
beego-简单项目写法--路径已经放进去了
Beego案例-新闻发布系统 1.注册 后台代码和昨天案例代码一致。,所以这里面只写一个注册的业务流程图。 **业务流程图 ** 2.登陆 业务流程图 登陆和注册业务和我们昨天登陆和注册基本一样,所以就不再重复写这个代码 但是我们遇到的问题是如何做代码的迁移&…...

Linux-CPU相关常用命令合集
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、cpu相关常用命令 二、cpuinfo 参数详细对照表 前言 本篇文章主要记录平时Linux-常用命令整理! 提示:以下是本篇文章正文内容&#…...
vue 百度地图/天地图设置铺满屏幕100%,解决空隙问题
设置100%无效,刷新依然右侧有空隙,解决:min-width: 100vw; <div class"aui-flex-col" style"width: 100%; height:100%"><div id"mapAllCon" style"width: 100%; min-width: 100vw; height: 10…...
)
第五章:最新版零基础学习 PYTHON 教程—Python 字符串操作指南(第六节 - Python 中字符串的逻辑运算符)
对于 python 中的字符串,布尔运算符(and、or、not)起作用。让我们考虑两个字符串,即 str1 和 str2,并在它们上尝试布尔运算符: Python3 str1 = str2 = geeks# 使用 repr 打印带引号的字符串# 返回 str1 print(repr(str1 and str2)) # 返回 str1 print(repr(str2 and…...
Bark Ai 文本转语音 模型缓存位置修改
默认缓存位置在:~/.cache 加入环境变量:XDG_CACHE_HOME,指定缓存位置 修改后新的位置为: D:\Ai\Bark\Bark Cache...
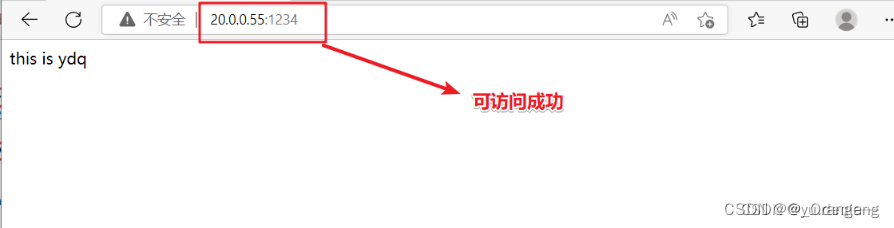
Docker 镜像的创建
目录 一、Docker镜像的创建 1、基于已有镜像创建 2、基于本地模板创建 3、基于dockerfile创建 3.1 dockerfile结构 3.2 构建镜像命令 二、镜像分层的原理 1、联合文件系统(UnionFS) 2、镜像加载的原理 三、Dockerfile 操作常用的指令 案例实验…...
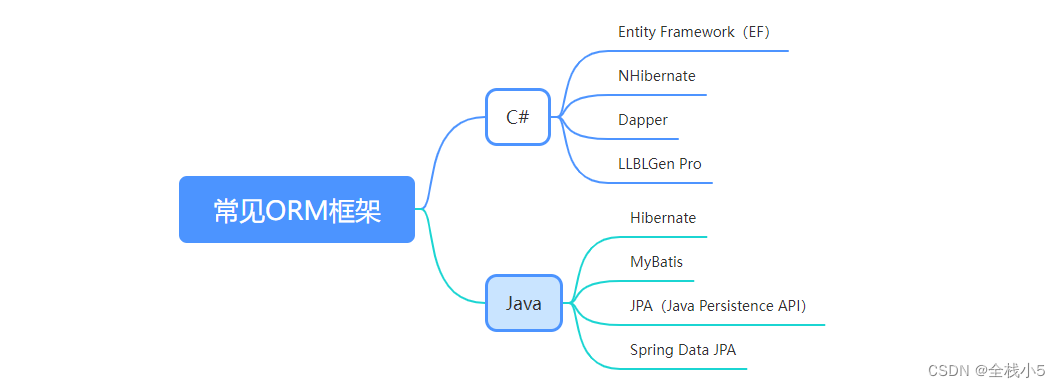
【ORM】浅聊C#和Java的ORM底层框架
给自己一个目标,然后坚持一段时间,总会有收获和感悟! 国庆假期马上结束,闲暇时间,突然对Ado.Net这个词的由来感兴趣,然后就一顿复习了一遍,顺便也了解了下java关于ORM框架的底层是什么ÿ…...
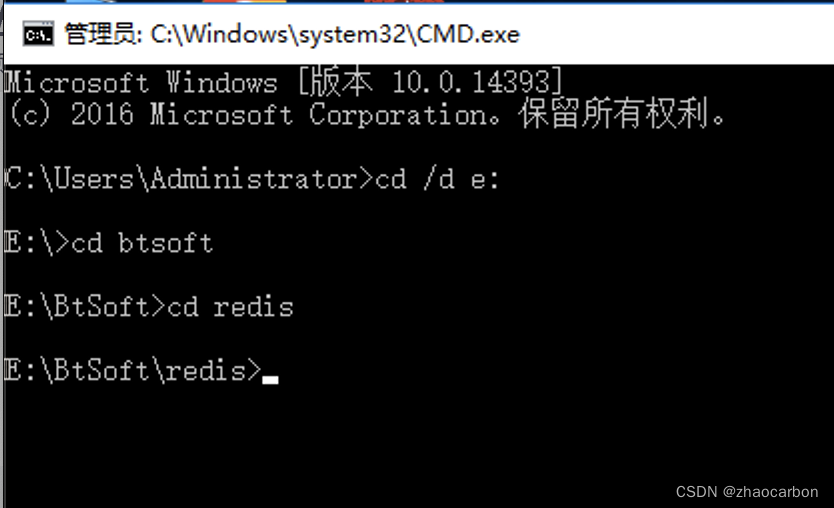
windows redis 自启动 Redis服务无法启动报错1067问题
如果你的系统服务里面已经有redis服务并且无法启动,则使用下面的命令卸载此服务 ! 1、停止Redis服务: redis-server --service-uninstall 2、删除系统服务 sc delete redis 进入到你的Redis安装目录,我的在以下目录,谨记此时不…...

Ubuntu Server CLI专业提示
基础 网络 获取所有接口的IP地址 networkctl status 显示主机的所有IP地址 hostname -I 启用/禁用接口 ip link set <interface> up ip link set <interface> down 显示路线 ip route 将使用哪条路线到达主机 ip route get <IP> 安全 显示已登录的用户 w…...

Centos7升级OpenSSH9.1
最近遇到了服务器漏洞,需要对服务器的OpenSSH版本进行升级,查阅了相关资料,总结出了一套比较简单的方案。中间遇到的个别问题也进行了记录,供大家参考。 下载准备 从https://ftp.jaist.ac.jp/pub/OpenBSD/OpenSSH/portable/opens…...
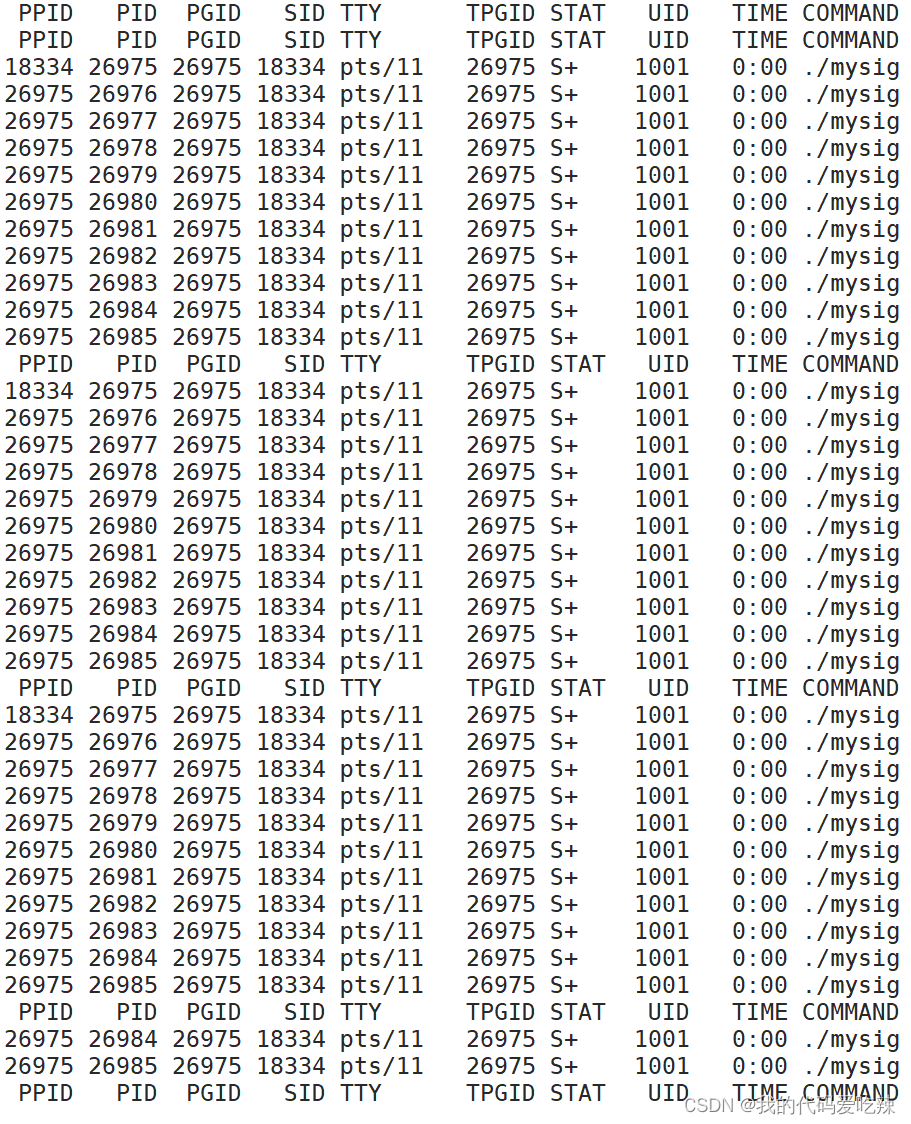
linux——信号
目录 一.信号的保存 二.信号集操作 1.信号集 2.信号集操作函数 3.sigprocmask 4.sigpending 三. 信号的捕捉 1.内核态和用户态 2. sigaction 四.可重入函数 五.SIGCHLD信号 一.信号的保存 实际执行信号的处理动作称为信号递达(Delivery)。信号从产生到递达之间的状…...
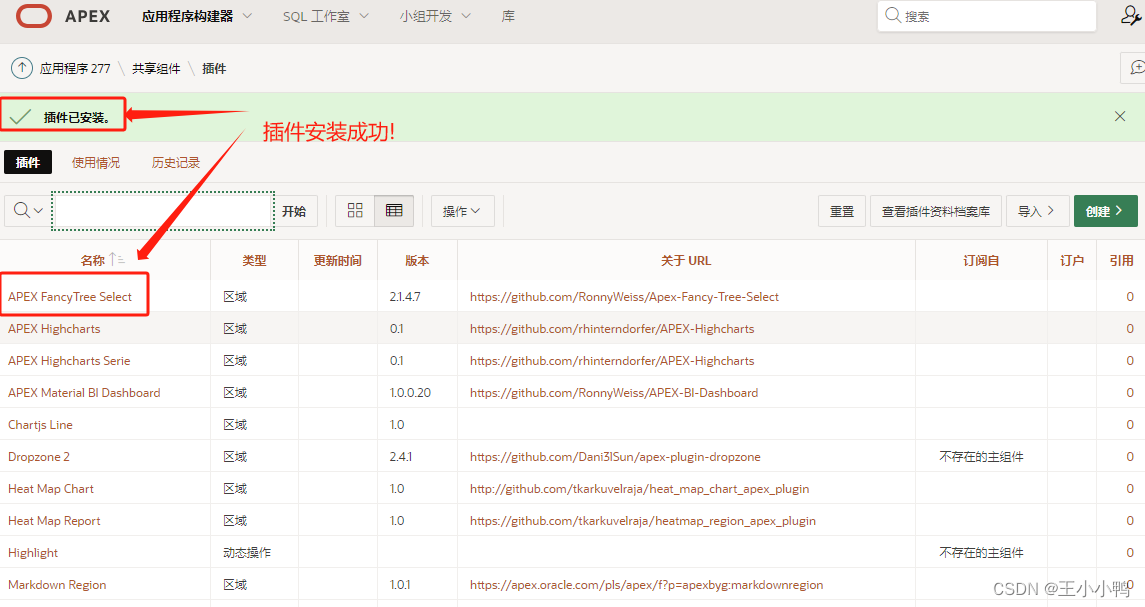
存档&改造【03】Apex-Fancy-Tree-Select花式树的导入及学习
Apex-Fancy-Tree-Select git学习网页 GitHub - RonnyWeiss/Apex-Fancy-Tree-Select: Fancy Tree Plug-in for Oracle APEX 如何从其他应用程序导出已有插件到新应用程序中 1.从其他应用程序导出插件 其他应用程序-【共享组件】-【插件】-【任务 导出插件】-选择想要导出的…...

【单片机】14-I2C通信之EEPROM
1.EEPROM概念 1.EEPROM 1.1 一些概念 (1)一些概念:ROM【只读存储器---硬盘】,RAM【随机访问存储器--内存】,PROM【可编程的ROM】,EPROM【可擦除ROM】,EEPROM【电可擦除ROM】 1.2 为什么需要EE…...
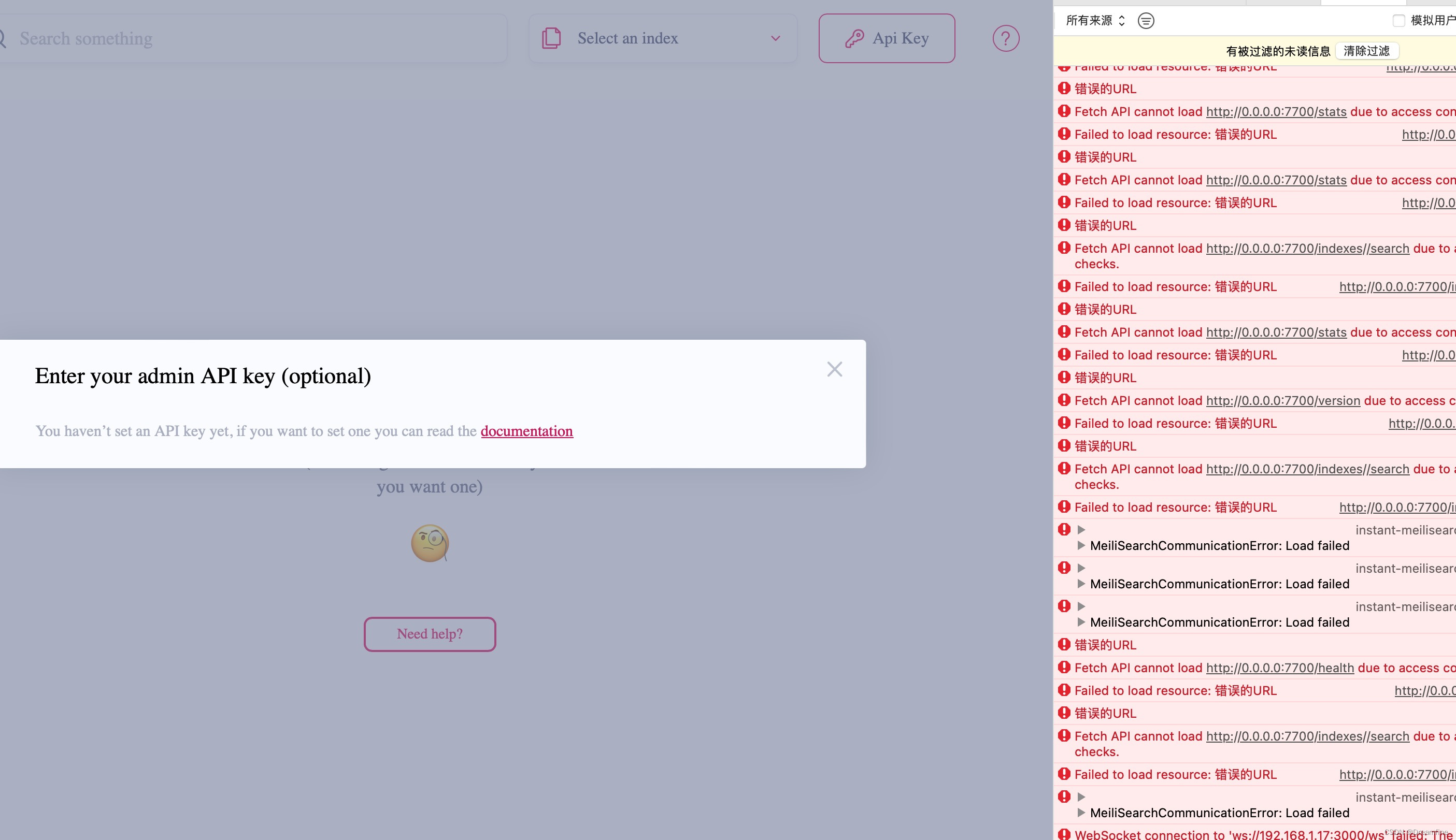
Mini-dashboard 和meilisearch配合使用
下载的meilisearch一般是development模式,内置客户端,修改客户端后需要重要全部编译,花时间太长了。前后端分离才是正道,客户端修改不用重新编译后端。 方法如下: 1、修改配置文件/etc/meilisearch.toml,…...

leetcode 886. 可能的二分法
给定一组 n 人(编号为 1, 2, …, n), 我们想把每个人分进任意大小的两组。每个人都可能不喜欢其他人,那么他们不应该属于同一组。 给定整数 n 和数组 dislikes ,其中 dislikes[i] [ai, bi] ,表示不允许将…...
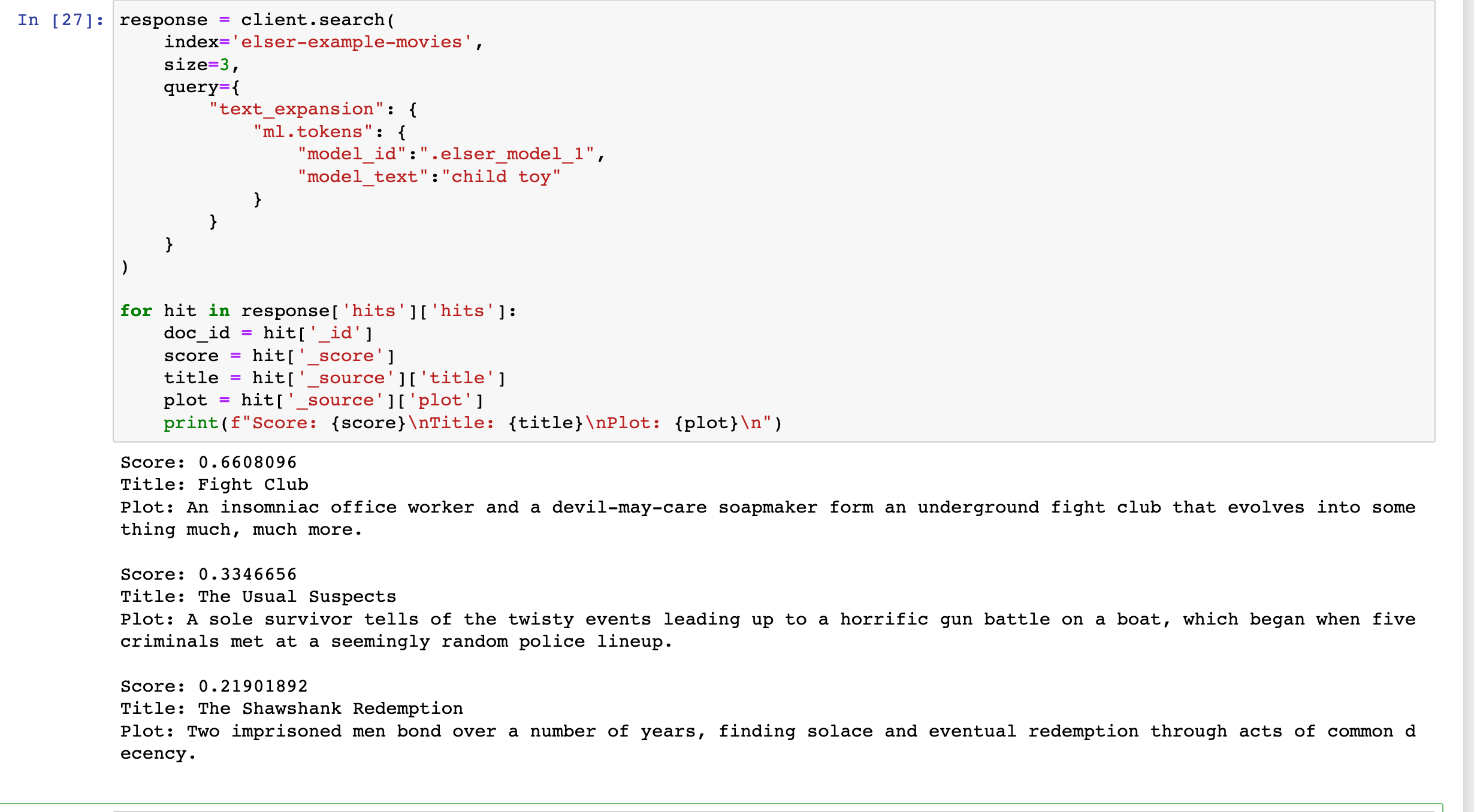
Elasticsearch:使用 ELSER 文本扩展进行语义搜索
在今天的文章里,我来详细地介绍如何使用 ELSER 进行文本扩展驱动的语义搜索。 安装 Elasticsearch 及 Kibana 如果你还没有安装好自己的 Elasticsearch 及 Kibana,请参考如下的链接来进行安装: 如何在 Linux,MacOS 及 Windows 上…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

