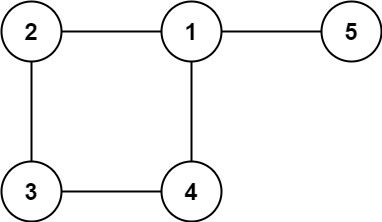
leetcode 886. 可能的二分法
给定一组 n 人(编号为 1, 2, …, n), 我们想把每个人分进任意大小的两组。每个人都可能不喜欢其他人,那么他们不应该属于同一组。
给定整数 n 和数组 dislikes ,其中 dislikes[i] = [ai, bi] ,表示不允许将编号为 ai 和 bi的人归入同一组。当可以用这种方法将所有人分进两组时,返回 true;否则返回 false。
示例 1:
输入:n = 4, dislikes = [[1,2],[1,3],[2,4]]
输出:true
解释:group1 [1,4], group2 [2,3]
示例 2:
输入:n = 3, dislikes = [[1,2],[1,3],[2,3]]
输出:false
示例 3:
输入:n = 5, dislikes = [[1,2],[2,3],[3,4],[4,5],[1,5]]
输出:false
提示:
1 <= n <= 2000
0 <= dislikes.length <= 104
dislikes[i].length == 2
1 <= dislikes[i][j] <= n
ai < bi
dislikes 中每一组都 不同
思路:用「染色法」来解决,第一组颜色标记为 1, 则相邻组的颜色标记为 2,遍历时,如果发现邻节点已经被染色,且和当前节点的颜色相同,说明是不能划分为两组的。
可采用 dfs 和 bfs 来做
import collections
class Solution:def dfs(self, color, f, index, co):color[index] = cofor x in f[index]:## 与3做异或,要么是 1,要么是2## 注意, 这儿不能直接写 return self.dfs(color, f, x, co^3)if color[x] == 0 and not self.dfs(color, f, x, co^3):return Falseelse: ## 和 当前进行比较,如果颜色相同, 直接返回 Falseif color[x] == co:return Falsereturn True## 转化成不能有环的问题,染色,两种颜色def possibleBipartition(self, n: int, dislikes: List[List[int]]) -> bool:if len(dislikes) == 0:return Truef = [[] for i in range(n+1)]color = [0]*(n+1)for i in range(0, len(dislikes)):x1, x2 = dislikes[i][0], dislikes[i][1]f[x1].append(x2)f[x2].append(x1)for i in range(1, n+1):if color[i] == 0:## 初始颜色设为 1, 设成 2 也 okif not self.dfs(color, f, i, 1):return Falsereturn True
bfs:
import collections
class Solution:## 转化成不能有环的问题def possibleBipartition(self, n: int, dislikes: List[List[int]]) -> bool:if len(dislikes) == 0:return True### 对已经遍历过&&并已加入 graph 的 index 做标记f = [[] for i in range(n+1)]vis = [0]*(n+1)for i in range(0, len(dislikes)):x1, x2 = dislikes[i][0], dislikes[i][1]f[x1].append(x2)f[x2].append(x1)for i in range(1, n+1):if vis[i] == 0:p = collections.deque()p.append((i, 1))while len(p) > 0:x1, color = p.popleft()vis[x1] = colornewColor = color^3for x in f[x1]:## 如果 x 没有被访问过if vis[x] == 0:p.append((x, newColor))else: ## 否则和当前的 colr 比较if color == vis[x]:return Falsereturn True
相关文章:

leetcode 886. 可能的二分法
给定一组 n 人(编号为 1, 2, …, n), 我们想把每个人分进任意大小的两组。每个人都可能不喜欢其他人,那么他们不应该属于同一组。 给定整数 n 和数组 dislikes ,其中 dislikes[i] [ai, bi] ,表示不允许将…...
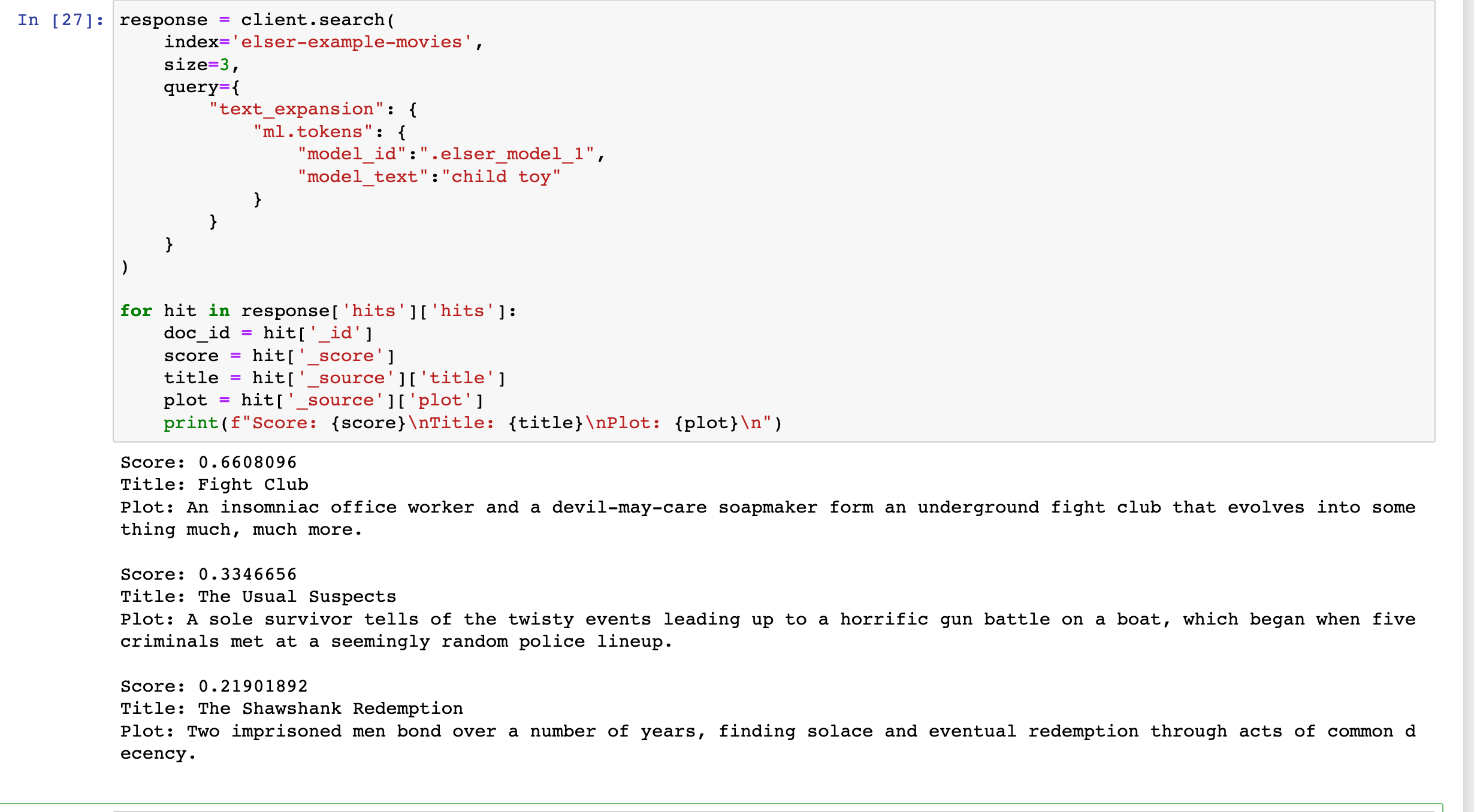
Elasticsearch:使用 ELSER 文本扩展进行语义搜索
在今天的文章里,我来详细地介绍如何使用 ELSER 进行文本扩展驱动的语义搜索。 安装 Elasticsearch 及 Kibana 如果你还没有安装好自己的 Elasticsearch 及 Kibana,请参考如下的链接来进行安装: 如何在 Linux,MacOS 及 Windows 上…...

OpenRadar DOA函数 Bartlett/CBF和Capon使用
Bartlett / CBF原理看这里 Capon原理看这里 这里只讲怎么调用openradar提供的aoa_bartlett和aoa_capon函数: 一些吐槽:虽然看起来openradar的作者代码水平很高,但里面有很多匪夷所思的写法,比如他demo里的解析文件格式就很迷啊等…...
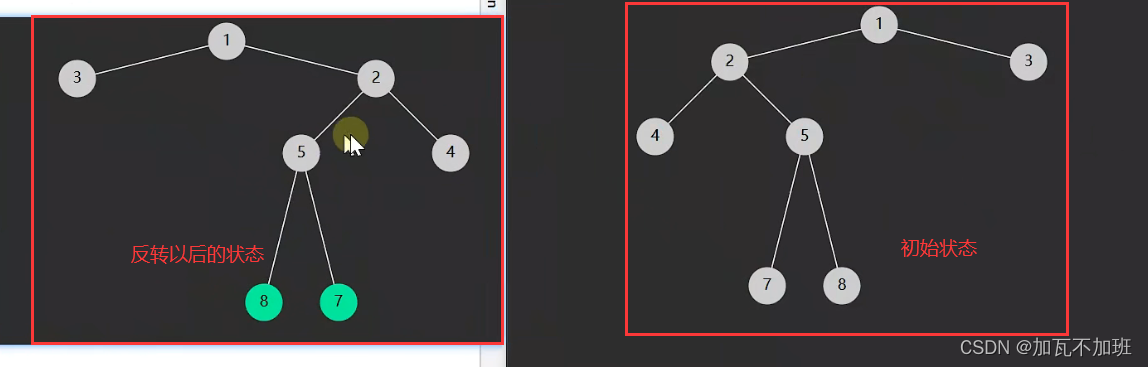
二叉树--翻转二叉树
文章前言:如果有小白同学还是对于二叉树不太清楚,作者推荐:二叉树的初步认识_加瓦不加班的博客-CSDN博客 给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。 如果思路不清楚,请看动态页面&am…...
强化学习环境 - robogym - 学习 - 3
强化学习环境 - robogym - 学习 - 3 文章目录 强化学习环境 - robogym - 学习 - 3项目地址为什么选择 robogymObservation - 观测信息Action - 动作信息Initialization - 初始状态设置 项目地址 https://github.com/openai/robogym 为什么选择 robogym 自己的项目需要做一些机…...
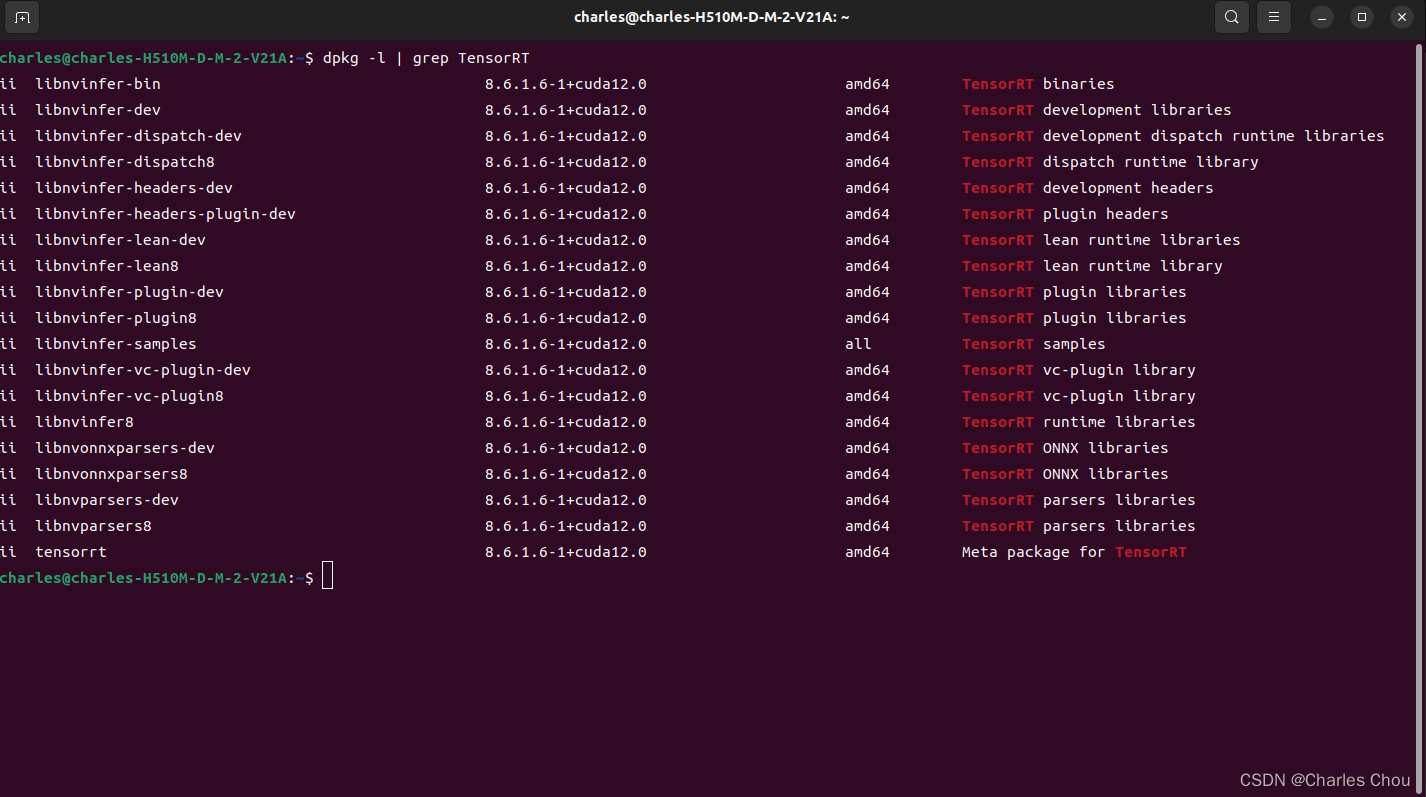
CUDA+cuDNN+TensorRT 配置避坑指南
深度学习模型加速部署的环境配置,需要在本地安装NVIDIA的一些工具链和软件包,这是一个些许繁琐的过程,而且一步错,步步错。笔者将会根据自己的经验来提供建议,减少踩坑几率。当然可以完全按照官方教程操作,…...
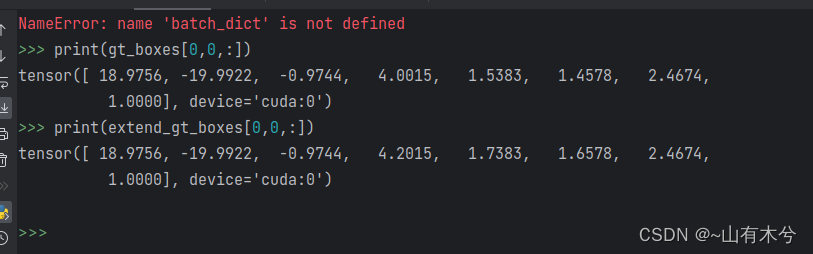
关于PointHeadBox类的理解
forward函数 def forward(self, batch_dict):"""Args:batch_dict:batch_size:point_features: (N1 N2 N3 ..., C) or (B, N, C)point_features_before_fusion: (N1 N2 N3 ..., C)point_coords: (N1 N2 N3 ..., 4) [bs_idx, x, y, z]point_labels (opti…...
ajax的使用)
javascript二维数组(10)ajax的使用
在JQuery中,使用AJAX的方法主要有以下几种: $.ajax():这是JQuery中最通用的AJAX请求方法。它需要一个包含各种参数的对象,其中包括请求的URL、请求方式、数据类型、请求参数等。请求成功后执行的回调函数也是通过参数来定义的。 …...

CMMI5认证哪些企业可以申请
CMMI5认证哪些企业可以申请 什么是CMMI5认证 CMMI(Capability Maturity Model Integration)是一种用于评估组织的软件工程能力的国际标准。CMMI模型包括5个等级,其中CMMI5是最高等级,代表组织具有达到持续优化和创新的能力。获得…...
【iptables 实战】9 docker网络原理分析
在开始本章阅读之前,需要提前了解以下的知识 阅读本节需要一些docker的基础知识,最好是在linux上安装好docker环境。提前掌握iptables的基础知识,前文参考【iptables 实战】 一、docker网络模型 docker网络模型如下图所示 说明࿱…...
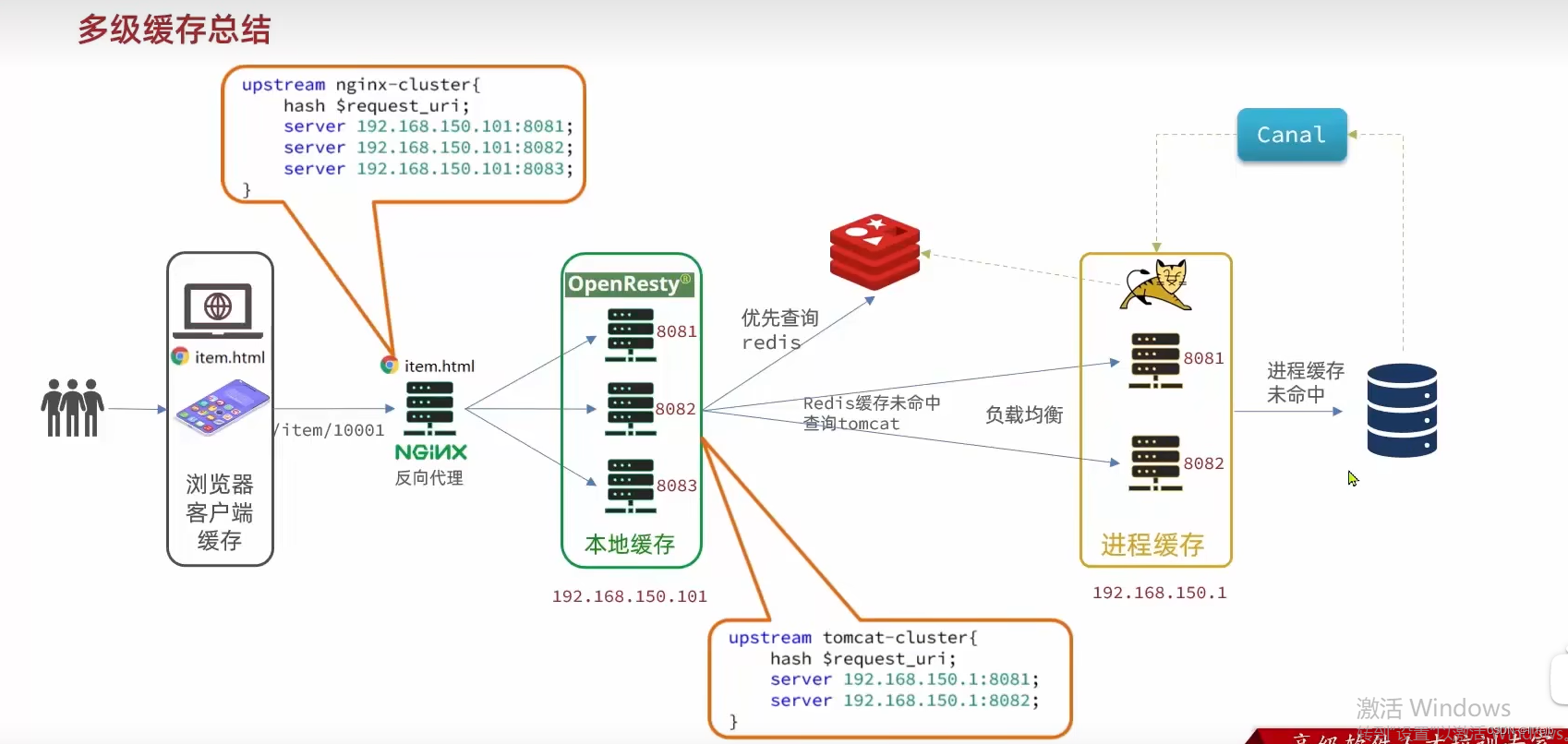
【多级缓存】
文章目录 1. JVM进程缓存2. Lua语法3. 实现多级缓存3.1 反向代理流程3.2 OpenResty快速入门 4. 查询Tomcat4.1 发送http请求的API4.2 封装http工具4.3 基于ID负载均衡4.4 流程小结 5. Redis缓存查询5.1 实现Redis查询 6. Nginx本地缓存6.1 本地缓存API6.2 实现本地缓存查询 7. …...
第五课 树与图
文章目录 第五课 树与图lc94.二叉树的中序遍历--简单题目描述代码展示 lc589.N叉树的层序遍历--中等题目描述代码展示 lc297.二叉树的序列化和反序列化--困难题目描述代码展示 lc105.从前序与中序遍历序列构造二叉树--中等题目描述代码展示 lc106.从中序与后序遍历序列构造二叉…...

2023-10-07 事业-代号z-副业-CQ私服-调研与分析
摘要: CQ作为一款运营了20年的游戏, 流传出的私服可以说是层出不穷, 到了现在我其实对这款游戏的长线运营的前景很悲观. 但是作为商业的一部分, 对其做谨慎的分析还是很有必要的. 传奇调研的来源: 一. 各种售卖私服的网站 传奇服务端版本库-传奇手游源码「免费下载」传奇GM论…...
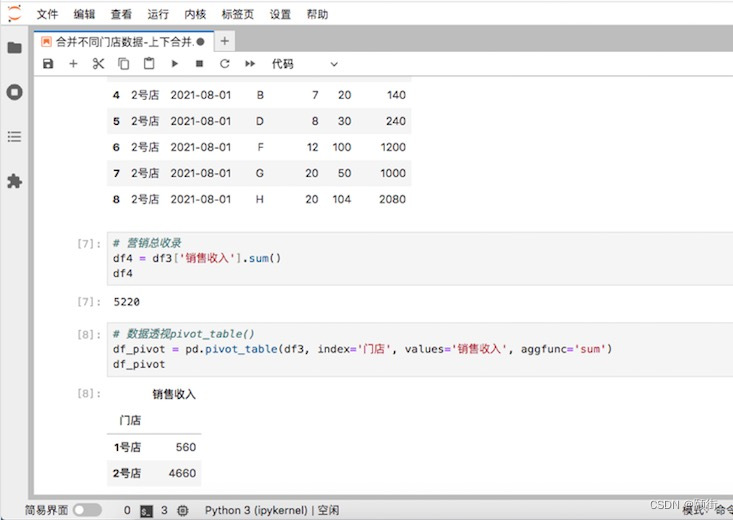
合并不同门店数据-上下合并
项目背景:线下超市分店,统计产品的销售数量和销售额,并用透视表计算求和 merge()函数可以根据链接键横向连接两张不同表,concat()函数可以上下合并和左右合并2种不同的合并方式。merge()函数只能横向连接两张表,而con…...

学习记忆——数学篇——案例——算术——整除特点
理解记忆法 对于数的整除特征大家都比较熟悉:比如4看后两位(因为100是4的倍数),8看后三位(因为1000是8的倍数),5末尾是0或5,3与9看各位数字和等等,今天重点研究一下3,9,…...

PHP8中的魔术方法-PHP8知识详解
在PHP 8中,魔术方法是一种特殊的方法,它们以两个下划线(__)开头。魔术方法允许您定义类的行为,例如创建对象、调用其他方法或访问和修改类的属性。以下是一些常见的魔术方法: __construct(): 类的构造函数…...

[图论]哈尔滨工业大学(哈工大 HIT)学习笔记23-31
视频来源:4.1.1 背景_哔哩哔哩_bilibili 目录 1. 哈密顿图 1.1. 背景 1.2. 哈氏图 2. 邻接矩阵/邻接表 3. 关联矩阵 3.1. 定义 4. 带权图 1. 哈密顿图 1.1. 背景 (1)以地球为建模,从一个大城市开始遍历其他大城市并且返回…...

Nginx+Keepalived实现服务高可用
Nginx 和 Keepalived 是常用于构建高可用性(High Availability)架构的工具。Nginx 是一款高性能的Web服务器和反向代理服务器,而Keepalived则提供了对Nginx服务的健康状态监测和故障切换功能。 下载Nginx 在服务器1和服务器2分别下载nginx …...
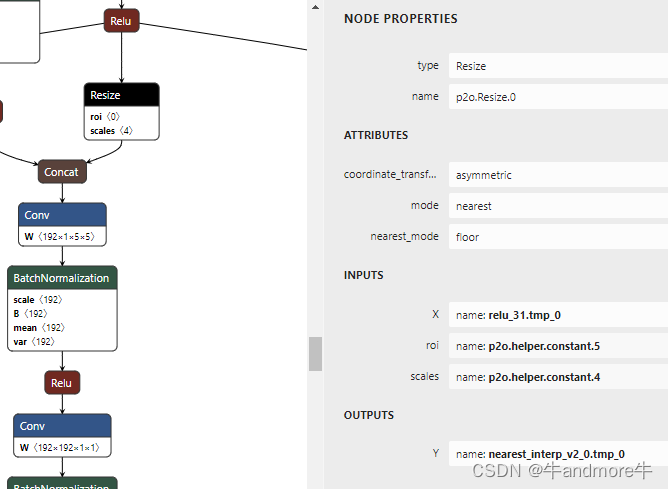
picodet onnx转其它芯片支持格式时遇到
文章目录 报错信息解决方法两模型精度对比 报错信息 报错信息为: Upsample(resize) Resize_0 not support attribute coordinate_transformation_mode:half_pixel. 解决方法 整个模型转换过程是:paddle 动态模型转成静态,再用paddle2onnx…...

【学习笔记】CF704B Ant Man
智商不够啊,咋想到贪心的😅 非常经典的贪心模型🤔 首先,从小到大将每个 i i i插入到排列中,用 D P DP DP记录还有多少个位置可以插入,可以通过钦定新插入的位置左右两边是否继续插入数来提前计算贡献。注…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...
