【图论】Linova and Kingdom—CF1336A
Linova and Kingdom—CF1336A
参考文章
思路
1 1 1 号节点为根节点。很容易想到,工业城市在树的下边,旅游城市在树的上边。具体来说,如果节点 u u u 是工业城市,那么它的子树的所有节点一定都是工业城市;如果节点 u u u 是旅游城市,那么它到根节点的路径上的所有城市都是旅游城市。
我们先把所有城市认定为工业城市,然后在与工业城市直接相连的旅游城市中选出“将其变为工业城市提供的贡献值”最大的城市,并将其变为工业城市。
城市的贡献的计算方法:当前点的子树的节点数 - (当前点的深度 - 1)。
可以利用用优先队列来选出最佳的城市,然后再将新产生的满足条件的城市压入队列。
由于我们选出的“贡献点最大的城市”的前提是这个点(设为 w w w 点)的子树上所有点都是工业城市,并且与根节点路径上的所有点都是旅游城市。那么如果后边的操作把 w w w 点的子节点给变成了旅游城市,那么不就不满足这个条件了吗?
请认真考虑我们是如何计算计算一个边界处的旅游城市如果变为工业城市后可以提供的贡献的:当前点的子树的节点数 - (当前点的深度 - 1)。 w w w 的贡献是相对于“ w w w 点及 w w w 点到根节点路径上都是旅游城市的条件”,也就是这种计算贡献的方法考虑了上一个状态,并非独立计算某一个点的贡献。
C o d e Code Code
#include <bits/stdc++.h>
#define int long long
#define sz(a) ((int)a.size())
#define all(a) a.begin(), a.end()
using namespace std;
using PII = pair<int, int>;
using i128 = __int128;
const int N = 2e5 + 10;int n, k;
int contri[N];void solve() {cin >> n >> k;vector<vector<int>> g(n + 1);for (int i = 1; i <= n - 1; i ++) {int a, b; cin >> a >> b;g[a].push_back(b);g[b].push_back(a);}// 计算深度和子树中节点数量vector<int> deep(n + 1, -1), son_num(n + 1);auto dfs = [&] (auto dfs, int u) ->int {int sum = 1;for (auto v : g[u]) {if (deep[v] == -1) {deep[v] = deep[u] + 1;sum += dfs(dfs, v);}}son_num[u] = sum;return sum;};deep[1] = 1;dfs(dfs, 1);// 计算每个点的贡献for (int i = 1; i <= n; i ++) {son_num[i] --;contri[i] = son_num[i] - (deep[i] - 1);}int res = 0;k = n - k;vector<int> st(n + 1, 0); // 标记是否为旅游城市/已经来过priority_queue<PII, vector<PII>> q; // [贡献,节点] 降序优先队列q.emplace(contri[1], 1);while (not q.empty() && k --) {auto [f, s] = q.top(); q.pop();st[s] = 1;res += f;for (auto v : g[s]) {if (not st[v]) {q.emplace(contri[v], v);}}}cout << " ";cout << res << "\n";
}signed main() {ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int T = 1;
// cin >> T; cin.get();while (T --) solve();return 0;
}
相关文章:

【图论】Linova and Kingdom—CF1336A
Linova and Kingdom—CF1336A 参考文章 思路 1 1 1 号节点为根节点。很容易想到,工业城市在树的下边,旅游城市在树的上边。具体来说,如果节点 u u u 是工业城市,那么它的子树的所有节点一定都是工业城市;如果节点 u…...
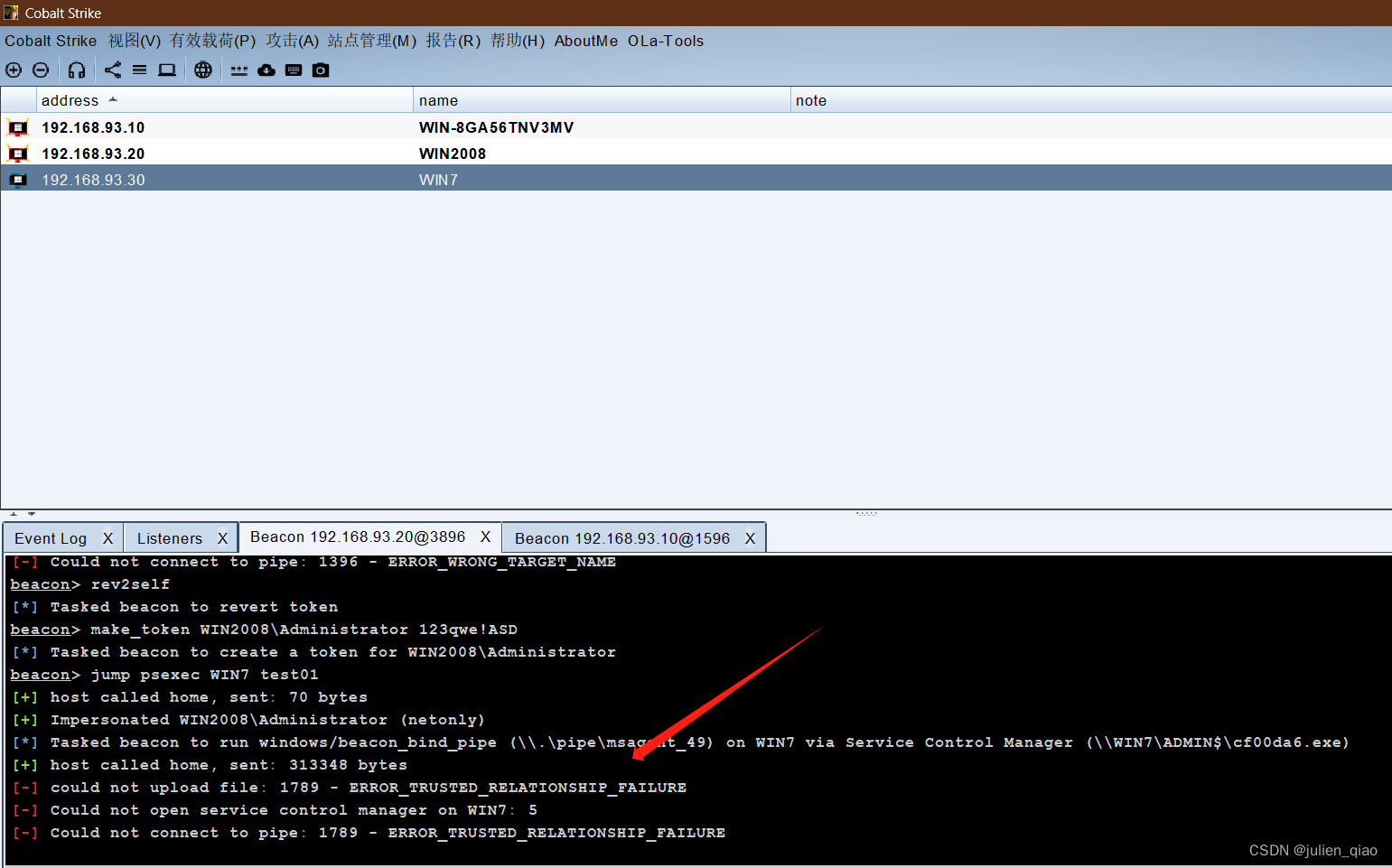
【红日靶场】vulnstack3-完整渗透过程
系列文章目录 【红日靶场】vulnstack1-完整渗透过程 【红日靶场】vulnstack2-完整渗透过程 【红日靶场】vulnstack3-完整渗透过程 文章目录 系列文章目录基本信息环境配置开始渗透信息收集暴力破解漏洞利用绕过内网信息收集尝试上线msf上线msf横向移动msf 传达会话给cs横向到域…...
)
物联网通信技术课程作业资料(TPUNB技术)
参考内容 TPUNB无线通信技术 - 技象科技 (techphant.cn) 技象科技CTO郑凛:用最好的物联网服务最多的人 | 了不起的创变者_技术_通信_团队 (sohu.com) LPWAN技术融合使用大势之下,TPUNB奔跑的一年-IOTE物联网展 (baidu.com) 院士认可国际首创…...
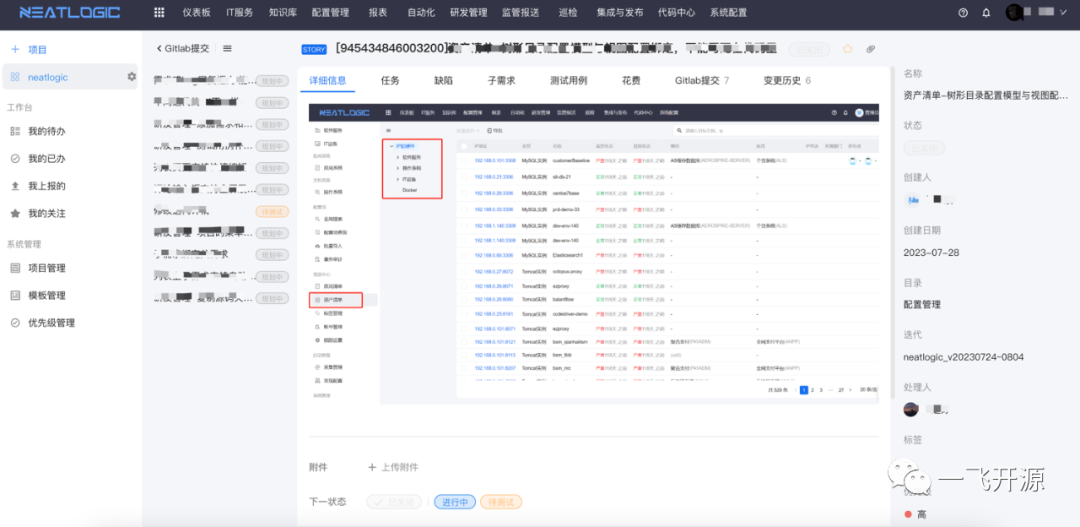
[开源]研发管理项目,支持从需求到代码发布全过程全生命周期管理
一、开源项目简介 neatlogic-rdm支持从需求到代码发布全过程覆盖。具备需求管理、缺陷追踪、测试计划、测试用例、报表仪表板等功能,支持关联外部代码库如GitLab、GitHub等。个性化的属性配置和状态流转控制,能帮助用户管理不同类型项目。 二、开源协议…...

一文生成猫眼电影热榜词云
1.爬取猫眼电影热榜数据 此次爬取的是电影票房的热榜电影名称,具体网站网址为猫眼电影热榜,经过实验观察后发现,此处的数据是通过ajax异步加载的,如果不相信可以使用request对当前网站网址发送请求,会发现无法获取电影…...

监控脚本展示
需求: 监控SVQC,SVCD,FHTC,FHQC,FHCD文件的生成 监控服务器:10.10.3.56 监控路径:/data/app/datafile/ftp/qdttec/10000002/download/yyyyMMdd/* 监控时间:每天7点开始,2…...
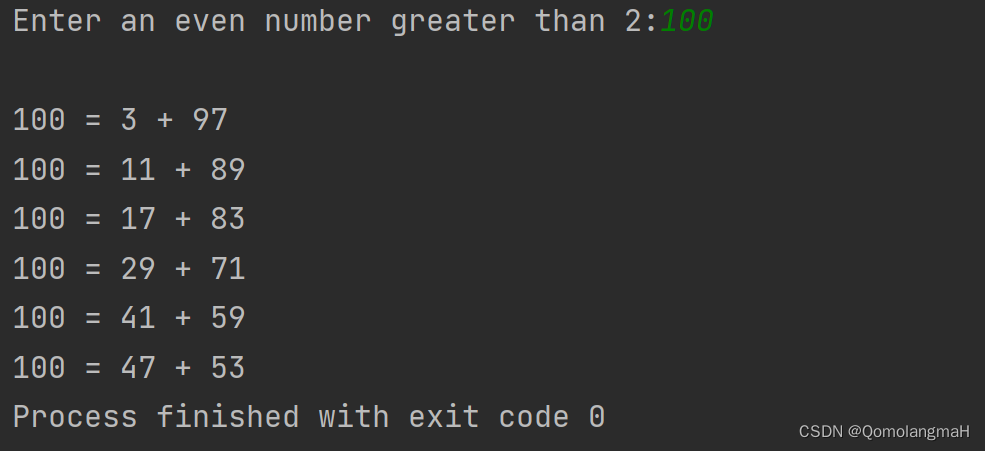
【重拾C语言】五、模块化程序设计——函数(定义、调用、参数传递、结果返回、函数原型;典例:打印字符图形、验证哥德巴赫猜想)
目录 前言 五、模块化程序设计——函数 5.1 计算三角形的重心 5.2 函数 5.2.1 函数定义 5.2.2 函数调用 a. 函数调用的形式和过程 b. 参数传递 值传递 指针传递 c. 函数结果返回 5.2.3 函数原型(先调用后定义) 5.3 程序设计实例 5.3.1 打印…...

Unity实现设计模式——迭代器模式
Unity实现设计模式——迭代器模式 迭代器模式是一种行为型设计模式,它提供了一种统一的方式来访问集合对象中的元素,而不是暴露集合内部的表示方式。简单地说,就是将遍历集合的责任封装到一个单独的对象中,我们可以按照特定的方式…...
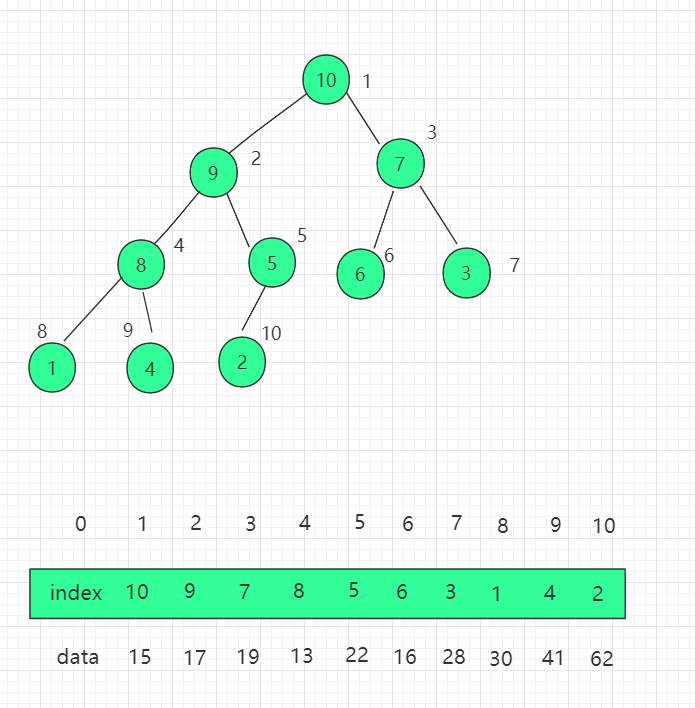
【数据结构与算法】之“堆”介绍
目录 堆的基本存储 一、概念及其介绍 二、适用说明 三、结构图示 堆的 shift up 堆的 shift down 基础堆排序 一、概念及其介绍 二、适用说明 三、过程图示 优化堆排序 索引堆及其优化 一、概念及其介绍 二、适用说明 三、结构图示 堆的基本存储 一、概念及其介…...
 使用GPU加速崩溃)
ncnn Fatal signal 11 (SIGSEGV) 使用GPU加速崩溃
如果你的报错堆栈中包含以下信息,其中的关键信息是 anon:dalvik-classes2.dex extracted in memory Fatal signal 11 (SIGSEGV), code 1 (SEGV_MAPERR), fault addr 0x3c in tid 8619 (eplabv3plusncnn), pid 8619 () 2023-10-07 15:48:31.395 9793-9793 DEBUG …...

计算机考研 | 2018年 | 计算机组成原理真题
文章目录 【计算机组成原理2018年真题44题-15分】【第一步:信息提取】【第二步:具体解答】 【计算机组成原理2018年真题45题-8分】【第一步:信息提取】【第二步:具体解答】 【计算机组成原理2018年真题44题-15分】 某计算机采用页…...

用Configuration注解的方式写一个java过滤器的详细实例?
在Java中,可以使用Configuration注解和Spring框架来创建和配置过滤器。下面是一个详细的示例: 首先,创建一个实现javax.servlet.Filter接口的过滤器类,例如MyFilter: import javax.servlet.*; import java.io.IOExce…...
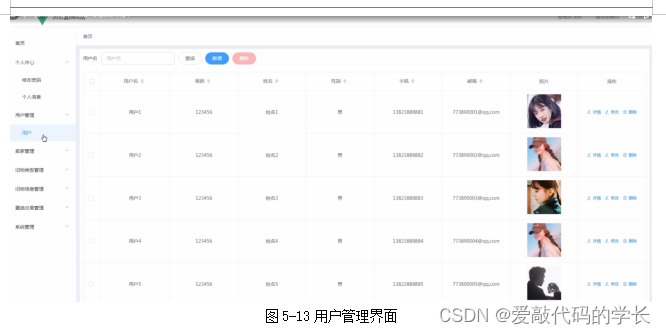
基于Springboot实现旧物置换网站平台演示【项目源码+论文说明】分享
基于Springboot实现旧物置换网站平台演示 摘要 随着时代在一步一步在进步,旧物也成人们的烦恼,许多平台网站都在推广自已的产品像天猫、咸鱼、京东。所以开发出一套关于旧物置换网站成为必需。旧物置换网站主要是借助计算机,通过对用户进行管…...

想要精通算法和SQL的成长之路 - 存在重复元素
想要精通算法和SQL的成长之路 - 存在重复元素 前言一. 存在重复元素II二. 存在重复元素III2.1 基于红黑树增删改查 前言 想要精通算法和SQL的成长之路 - 系列导航 一. 存在重复元素II 原题链接 思路: 我们用HashSet存储元素,做到去重的效果。同时存储…...
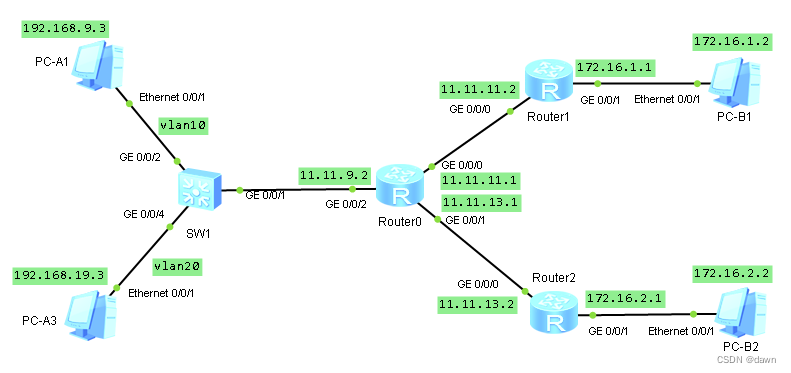
使用华为eNSP组网试验⑸-访问控制
今天练习使用华为sNSP模拟网络设备上的访问控制,这样的操作我经常在华为的S7706、S5720、S5735或者H3C的S5500、S5130、S7706上进行,在网络设备上根据情况应用访问控制的策略是一个网管必须熟练的操作,只是在真机上操作一般比较谨慎ÿ…...
iPhone苹果手机闹钟智能跳过节假日怎么设置?
国内绝大多数的手机用户使用的操作系统只有三个,安卓、鸿蒙和苹果的ios。而iPhone苹果手机的忠实用户是非常多的,所以日积月累中用户数量也就非常庞大,并且相当一部分用户都是上班族。而工作忙碌的上班族因为事情比较多,为了避免自…...
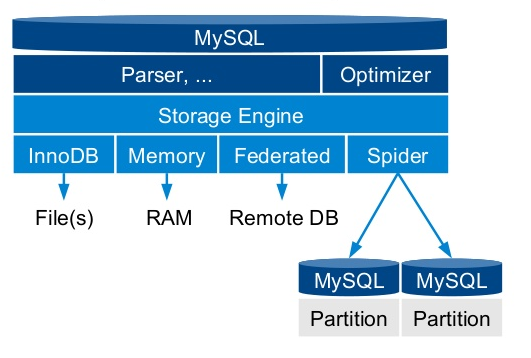
TenDB Cluster 简介
文章目录 1.简介2.TSpider3.TenDB4.Tdbctl5.TenDB Cluster Operator参考文献 1.简介 TenDB Cluster 是腾讯游戏 CROS DBA 团队提供的 MySQL 分布式关系型数据库解决方案。主要特点包括:透明分库分表、高可用的 MySQL 集群服务,透明及在线的扩容及缩容&a…...
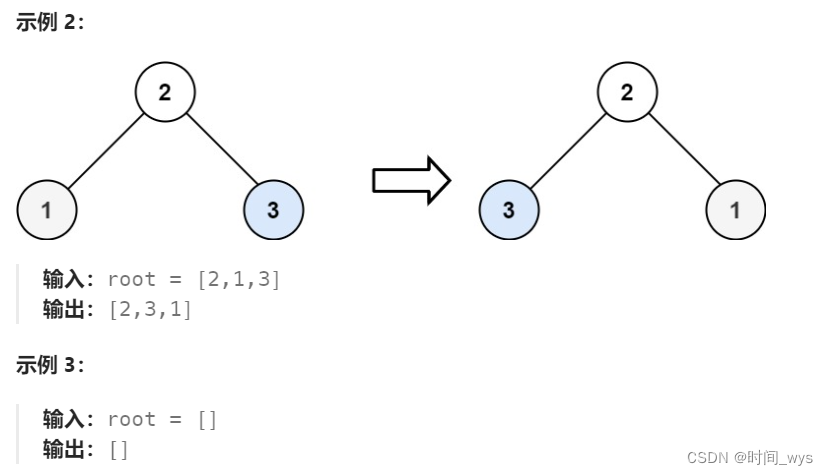
【刷题笔记10.6】LeetCode:翻转二叉树
LeetCode:翻转二叉树 一、题目描述 给你一颗二叉树的根节点root,翻转这颗二叉树,并返回其根节点。 二、分析 我们在做二叉树题目时候,第一想到的应该是用 递归 来解决。 仔细看下题目的 输入 和 输出,输出的左右…...
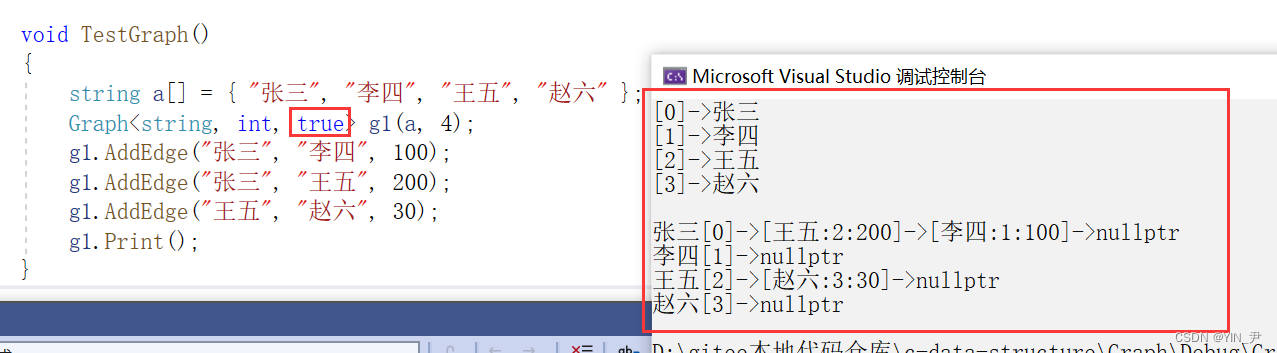
【高阶数据结构】图详解第一篇:图的基本概念及其存储结构(邻接矩阵和邻接表)
文章目录 1. 图的基本概念1.1 什么是图1.2 有向图和无向图1.3 完全图1.4 邻接顶点1.5 顶点的度1.6 路径1.7 路径长度1.8 简单路径与回路1.9 子图1.10 连通图1.11 强连通图1.12 生成树 2. 图的存储结构2.1 邻接矩阵2.2 邻接矩阵代码实现结构定义构造函数添加边打印图测试 2.3 邻…...

IPV4跟IPV6的区别
如今互联网快速发展ipv4已经满足不了现在的需求,那么这时候就需要用更大的地址空间来代替,这时候ipv6就可以满足这一需求,相比ipv4它有更大的地址空间可供使用。下面我将分享一下有何区别。 IPv4与IPv6之间的区别: 1、地址长度的区别:IPv4具…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...
