当前位置：首页 > news >正文

[图论]哈尔滨工业大学（哈工大 HIT）学习笔记16-22

news 2026/2/9 14:45:45

视频来源：2.7.1 补图_哔哩哔哩_bilibili

目录

1. 补图

1.1. 补图

2. 双图

2.1. 双图定理

3. 图兰定理/托兰定理

4. 极图理论

5. 欧拉图

5.1. 欧拉迹

5.2. 欧拉闭迹

5.3. 欧拉图

5.4. 欧拉定理

5.5. 伪图

1. 补图

1.1. 补图

（1）补图示例：其中G为母图，G'为其补图

（2）定义：设 $G=\left ( V,E \right )$ , 则 $G$ 的补图 $G{}'=\left ( V,E{}' \right )$ , 其中 $E{}'=\mathbb{P}_{2}\left ( V \right )\setminus E$ （所有顶点关联边二元集不包含 $E$ 的子集）

（3）推论： $G$ 和它的补图 $G{}'$ 有可能同构，即 $G\cong G{}'$

（4）例题：六个人的团体中，或有三个人互相认识，或有三个人互相不认识。可用图和补图来做。

（5）拉姆齐定理：要找这样一个最小的数n，使得n个人中必定有k个人相识或l个人互不相识

$\begin{aligned} &R\left(1,k\right) =1 \\ &R\left(2,k\right) =k \\ &R\left(p,q\right) =R\left(q,p\right) \\ &R\left(p,q\right) \leq R\left(p-1,q\right)+R\left(p,q-1\right)\textit{ if }p,q\geq2 \\ &R\left(p,q\right) \leq\binom{p+q-2}{p-1} \end{aligned}$

2. 双图

2.1. 双图定理

（1）只用一刀切开所有边就好了，看边的两边是否在不同子图中。

（2）定理1：双图也称2部图，其中圈的度数一定为偶数（充分必要条件）。

证明：圈可以表示成 $v_{1},v_{2},v_{3},...,v_{n},v_{1}$ ，若 $v_{1}\in V$ ，则 $v_{2}\in V{}'$ 。因此单数顶点都属于 $V$ ，偶数顶点都属于 $V{}'$

（2）定理2：有 $G= \left ( V,E \right )$ ， $\exists v\in V$ ， $deg\, v> 0$ ， $\forall v\in V$ ， $deg\, v$ 为偶数，则图中一定有圈

3. 图兰定理/托兰定理

（1）定理：设 $G= \left ( V,E \right )$ 是一个 $\left ( p,q \right )$ 图，如其中没有三角形，则 $q\leq \left [ \frac{p^{2}}{4} \right ]$ 。其中中括号为求整符号

（2）证明：显然，对于p=1,2,3时结论都成立。则分别证明p为奇数（p=2n-1）和偶数（p=2n）的情况；

假设p=2n-1时成立，则需证p=2n+1时成立

设p=2n-1的图G’，p=2n+1的图为G，有G-u-v=G';（u和v为两个顶点，若u,v连接，则它们一定没有公共邻接点，否则构成三角形；若它们不邻接，则可能存在公共邻接点。视频中老师应该是使他们邻接的，这样可以使第一个顶点u的邻接边假设到最大）

知G'是一个(2n-1,q')图，知 $q{}'\leq \left [\frac{\left ( 2n-1 \right )^{2}}{4} \right ]=n^{2}-n$ ;

$deg\, u=k,deg\, v\leq p-k$ （u和v邻接，且无公共邻接点的情况）

$q\leq q{}'+p \Rightarrow q\leq q{}'+2n\Rightarrow q\leq n^{2}+n\Rightarrow q\leq\left [ \frac{\left ( 2n+1 ^{2}\right )}{4} \right ]$

4. 极图理论

（1）找到边最多的图，但不含 $K_{n}$

5. 欧拉图

5.1. 欧拉迹

（1）定义：包含图的每一条边的迹

5.2. 欧拉闭迹

（1）定义：包含图的所有顶点的闭迹

5.3. 欧拉图

（1）定义：包含欧拉闭迹的图称为欧拉图

5.4. 欧拉定理

（1）定理1：G是欧拉图⇔G连通且每个顶点度为偶数

（2）定理2：图中有一条欧拉开迹⇔G中恰有2个奇度顶点

（3）定理3：设G有2n个奇度顶点，则G至少有n条迹

5.5. 伪图

（1）多重图定义：两个顶点可以之间有多条边

（2）带环图定义：存在顶点到自身的边

（3）伪图：包含多重图和带环图

相关文章：

[图论]哈尔滨工业大学（哈工大 HIT）学习笔记16-22

视频来源：2.7.1 补图_哔哩哔哩_bilibili 目录 1. 补图 1.1. 补图 2. 双图 2.1. 双图定理 3. 图兰定理/托兰定理 4. 极图理论 5. 欧拉图 5.1. 欧拉迹 5.2. 欧拉闭迹 5.3. 欧拉图 5.4. 欧拉定理 5.5. 伪图 1. 补图 1.1. 补图 （1）…...

编程日记 2023/10/7 22:22:08

使用关键字abstract 声明抽象类-PHP8知识详解

抽象类只能作为父类使用，因为抽象类不能被实例化。抽象类使用关键字abstract 声明，具体的使用语法格式如下： abstract class 抽象类名称{ //抽象类的成员变量列表 abstract function 成员方法1(参数); //抽象类的成员方法 abstract functi…...

编程日记 2023/10/7 22:18:02

Java中使用正则表达式

正则表达式正则表达式（Regular Expression）是一种用于匹配、查找和替换文本的强大工具。它由一系列字符和特殊字符组成，可以用来描述字符串的模式。在编程和文本处理中，正则表达式常被用于验证输入、提取信息、搜索和替换文本等…...

编程日记 2023/10/7 22:16:00

Python之字符串分割替换移除

Python之字符串分割替换移除分割 split(sepNone, maxsplit-1) -> list of strings 从左至右sep 指定分割字符串，缺省的情况下空白字符串作为分隔符maxsplit 指定分割的次数，-1 表示遍历整个字符串立即返回列表 rsplit(sepNone, maxsplit-1) -> …...

编程日记 2023/10/7 22:15:00

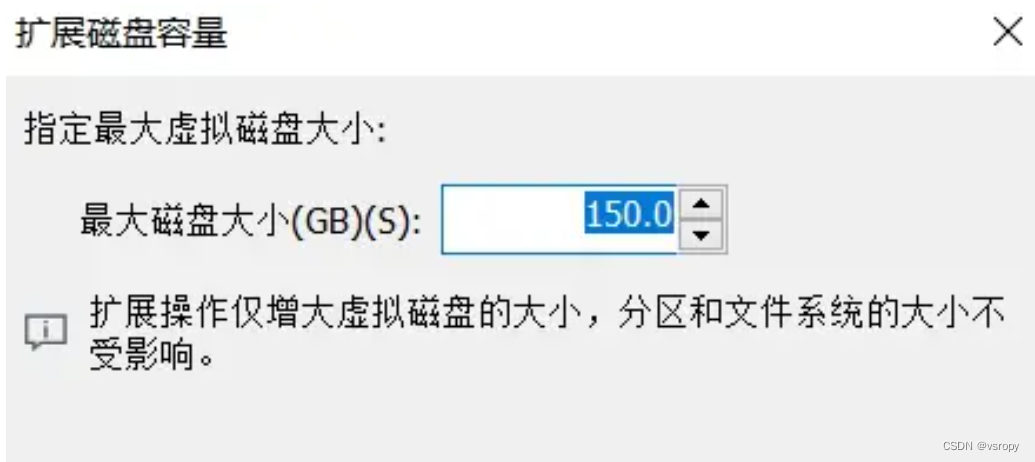
ubuntu增加内存

文章目录 1、硬盘操作步骤第二步：点击【扩展】（必须关闭ubuntu电源才能修改）第三步：修改【最大磁盘容量大小】1、硬盘操作步骤最近发现Ubuntu空间不足，怎么去扩容呢？第一步：点击【硬盘】第二步：点击【扩展】（必须关闭ubuntu电源才能修改）第三步：修改【最大磁…...

编程日记 2023/10/7 22:12:58

黑客都是土豪吗？真实情况是什么？

黑客的利益链条真的这么大这么好么,连最外围的都可以靠信息不对称赚普通人大学毕业上班族想都不敢想的金钱数目,黑客们是不是基本都是土豪网络技术可以称为黑客程度的技术是不是真的很吃香？如果大部分大学生的智力资源都用在学习网络技术，会不会出现僧…...

编程日记 2023/10/7 22:10:54

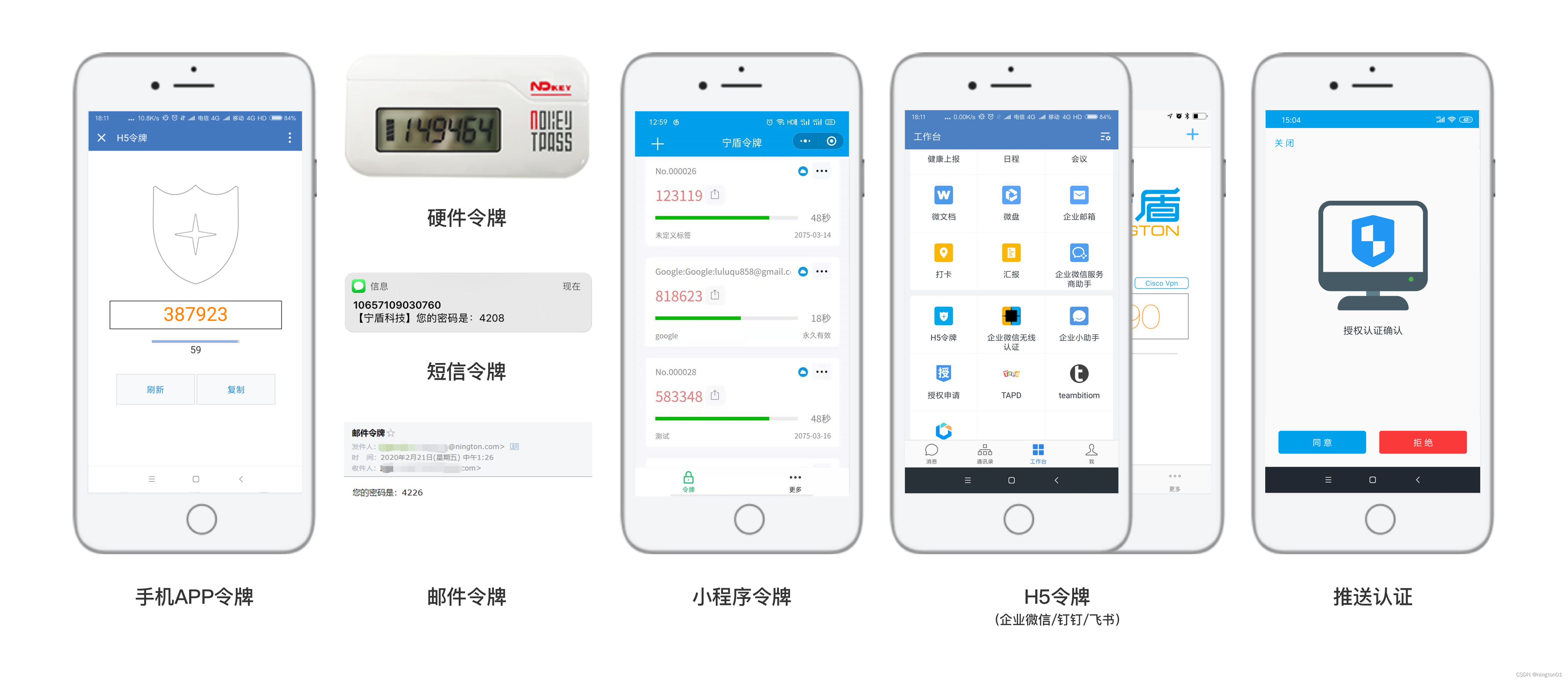
企业想过等保，其中2FA双因素认证手段必不可少

随着信息技术的飞速发展，网络安全问题日益凸显。等保2.0时代的到来，意味着企业和组织需要更加严格地保护自身的信息安全。而在这个过程中，双因素认证的重要性逐渐得到广泛认可。本文将探讨 2FA 双因素认证的重要性。在了解 2FA 双因素认证的…...

编程日记 2023/10/7 22:08:51

Combination Lock

题目描述新学期开学，您又回到了学校。您需要记住如何操作储物柜上的组合锁。一个组合锁的常见设计如图 1 所示。组合锁有一个圆形刻度表盘，在表盘上，有 40 个编号为从 0 至 39 的刻度，正上方有一个刻度指针。一个组合由这些数字…...

编程日记 2023/10/7 22:07:50

SpringBoot解决LocalDateTime返回数据为数组问题

现象： 在SpringBoot项目中，接口返回的数据出现LocalDateTime对象被转换成了数组原因分析： 默认序列化情况下会使用SerializationFeature.WRITE_DATES_AS_TIMESTAMPS。使用这个解析时就会打印出数组。解决方法： 在配置类中…...

编程日记 2023/10/7 22:06:49

【数字人】2、MODA | 基于人脸关键点的语音驱动单张图数字人生成（ICCV2023）

文章目录一、背景二、方法2.1 问题描述和数据预处理2.2 Mapping-Once network with Dual Attentions2.3 Facial Composer Network2.4 使用 TPE 来合成人像图片三、效果3.1 训练细节3.2 数据3.3 测评指标3.4 结果比较四、代码4.1 数据前处理4.2 训练4.3 推理论文&#xff1a…...

编程日记 2023/10/7 22:03:45

群狼调研（长沙物业第三方评优）开展房地产市场调查内容设计

湖南房地产市场近年来表现出多元化的发展趋势。为了在竞争激烈的市场中获得更好的发展，房地产企业需要密切关注市场变化，合理规划开发项目，同时提高产品质量和服务水平，以满足消费者的需求和期望。群狼调研(长沙神秘顾客调查)在房…...

编程日记 2023/10/7 22:01:43

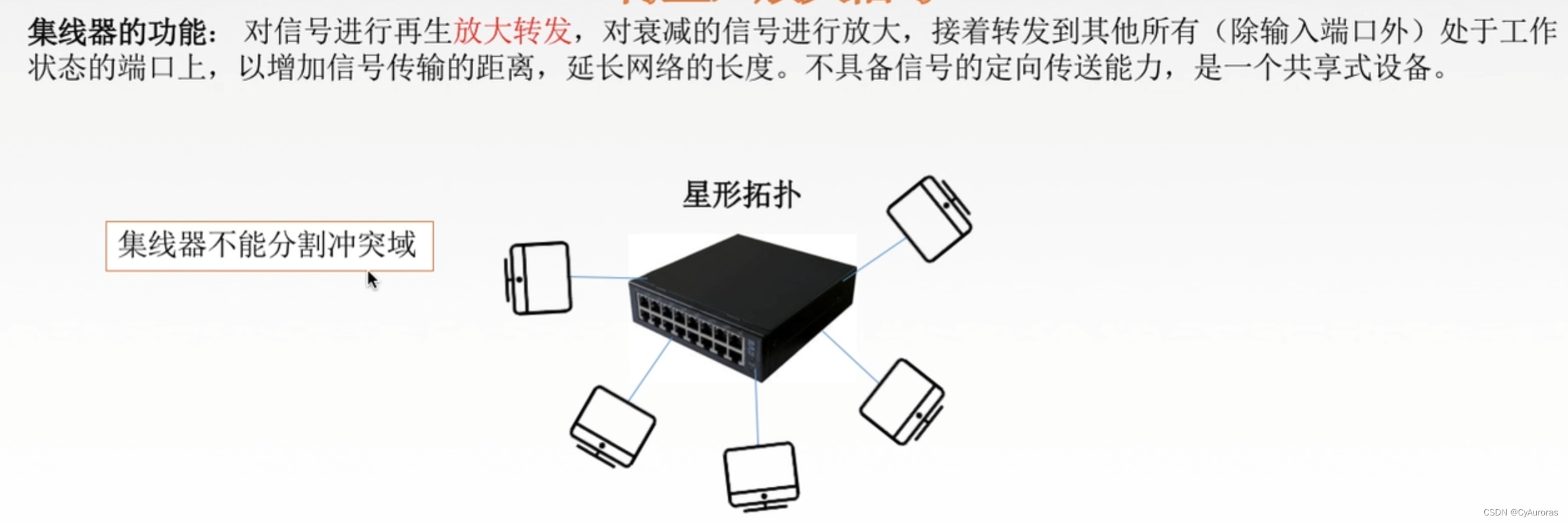
计算机网络-计算机网络体系结构-物理层

目录一、通信基础通信方式传输方式码元传输率 *二准则 2.1奈氏准则(奈奎斯特定理) 2.2香农定理三、信号的编码和调制 *数字数据->数字信号数字数据->模拟信号模拟数据->数字信号模拟数据->模拟信号 *四、数据交换方式电路交换报文交换…...

编程日记 2023/10/7 22:00:42

微信小程序wxs标签在wxml文件中编写JavaScript逻辑

PC端开发可以在界面中编写JavaScript脚本 vue/react这些框架更是形成了一种常态因为模板引擎和jsx语法本身就都是在js中的我们小程序中其实也有类似的奇妙写法不过先声明这东西不是很强大我们可以先写一个案例代码 wxml代码参考 <view><wxs module"wordSt…...

编程日记 2023/10/7 21:59:40

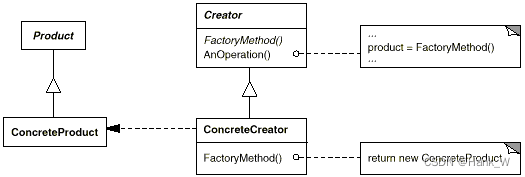
C++设计模式-工厂模式（Factory Method）

目录 C设计模式-工厂模式（Factory Method） 一、意图二、适用性三、结构四、参与者五、代码 C设计模式-工厂模式（Factory Method） 一、意图定义一个用于创建对象的接口，让子类决定实例化哪一个类。Factory…...

编程日记 2023/10/7 21:58:39

八大排序算法

#include<iostream> #include<cstring> #include<algorithm> using namespace std; const int N1e510; int q[N]; int w[N],s[N]; int n,sz; //直接插入排序 ,对于某一个元素加入到一个有序的序列中，将该元素依次从该位置开始 //从后往前比较&…...

编程日记 2023/10/7 21:51:29

机器学习笔记 - 两个静态手势识别的简单示例

一、关于手势识别手势识别方法通常分为两类：静态或动态。静态手势是那些只需要在分类器的输入处处理单个图像的手势，这种方法的优点是计算成本较低。动态手势需要处理图像序列和更复杂的手势识别方法。进一步了解可以参考下面链接。静态手势识别和动态手势识别的区别和技…...

编程日记 2023/10/7 21:48:26

2023年，有哪些好用的互联网项目管理软件？

项目管理是为了使工作项目能够按照预定的需求、成本、进度、质量顺利完成，而对人员、产品、过程和项目进行分析和管理的活动。一直以来，项目管理被企业管理人员和各级人员所重视，项目管理是一个项目的灵魂，只有做好了项目管理&am…...

编程日记 2023/10/7 21:45:19

python 按照文件大小读取文件

返回一个list，每个list里面是一个元组(filename, file_size)，按照file_size从小到大排序的 import osdef get_sorted_files(dir_path):# 存储最后的文件路径files []# 便利dir_path下面的文件或者文件夹for file in os.listdir(dir_path):file_path o…...

编程日记 2023/10/7 21:44:19

黑客帝国代码雨

黑客帝国代码雨奉上,之前一直想写,但一直没抽出时间来,今天把他写了,也算了了装心事效果图如下原理就不讲了,代码写的很清楚而且不长有不懂的评论区问我就好 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8">&l…...

编程日记 2023/10/7 21:43:18

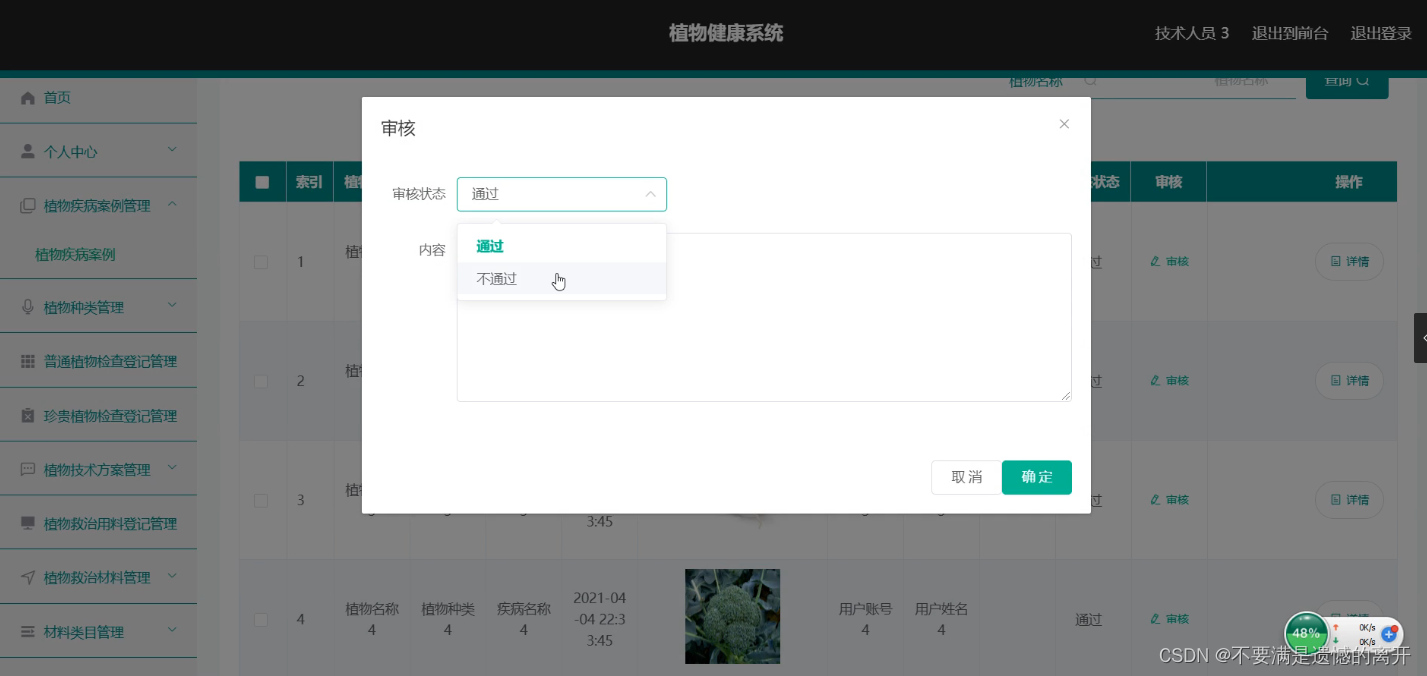
基于SpringBoot的植物健康系统

目录前言一、技术栈二、系统功能介绍系统首页咨询专家普通植物检查登记珍贵植物检查登记植物救治用料登记植物救治材料管理植物疾病案例管理三、核心代码 1、登录模块 2、文件上传模块 3、代码封装前言随着信息技术在管理上越来越深入而广泛的应用&am…...

编程日记 2023/10/7 21:40:16

【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15

缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下： struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

编程新知 2025/11/27 21:52:13

MFC内存泄露

1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

编程新知 2026/1/22 15:14:25

如何在看板中体现优先级变化

在看板中有效体现优先级变化的关键措施包括：采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中，设置任务排序规则尤其重要，因为它让看板视觉上直观地体…...

编程新知 2026/1/23 12:42:28

SCAU期末笔记 - 数据分析与数据挖掘题库解析

这门怎么题库答案不全啊日来简单学一下子来一、选择题（可多选） 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘：专注于发现数据中…...

编程新知 2026/1/24 14:15:43

leetcodeSQL解题：3564. 季节性销售分析

leetcodeSQL解题：3564. 季节性销售分析题目： 表：sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

编程新知 2025/10/5 19:58:27

Spring AI 入门：Java 开发者的生成式 AI 实践之路

一、Spring AI 简介在人工智能技术快速迭代的今天，Spring AI 作为 Spring 生态系统的新生力量，正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务（如 OpenAI、Anthropic）的无缝对接&…...

编程新知 2025/12/25 18:03:56

大数据学习（132）-HIve数据分析

🍋🍋大数据学习🍋🍋 🔥系列专栏： 👑哲学语录: 用力所能及，改变世界。 💖如果觉得博主的文章还不错的话，请点赞👍收藏⭐️留言&#x1f4…...

编程新知 2025/10/7 8:52:21

今日学习：Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存

文章目录优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因常见解决方法更好的解决方法设计精妙之处登录续期登录续期常见实现方式特…...

编程新知 2026/1/27 16:41:02

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南

1. 项目概述本跑酷小游戏基于鸿蒙HarmonyOS 5开发，使用DevEco Studio作为开发工具，采用Java语言实现，包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

编程新知 2025/12/19 22:56:05

Typeerror: cannot read properties of undefined (reading ‘XXX‘)

最近需要在离线机器上运行软件，所以得把软件用docker打包起来，大部分功能都没问题，出了一个奇怪的事情。同样的代码，在本机上用vscode可以运行起来，但是打包之后在docker里出现了问题。使用的是dialog组件，…...

编程新知 2025/9/24 3:05:06