当前位置： 首页 > news >正文

模拟滤波器的基础知识和设计

news 2025/7/3 18:45:49

信号处理工作中滤波器的应用是非常广泛的，可以分成模拟滤波器和数字滤波器两种，数字滤波器主要包括两种，IIR和FIR，这两种滤波器后面统一说，今天先来说一说模拟滤波器（主要是我先用Python实现了Matlab书里面模拟滤波器的一些内容）。

首先，什么是滤波器，什么又是模拟滤波器？

滤波器：具有频率选择作用的电路或者运算处理系统，具有滤除噪声、分离不同信号的功能，今天主要写的是，1、巴特沃斯滤波器、2、切比雪夫滤波器，3、椭圆滤波器，4、低通到低通的频带转换

模拟滤波器：更具一组设计规范来设计模拟系统函数H_a(s),使其逼近某个理想滤波器的特性。

各种模拟滤波器的设计过程都是先设计出低通滤波器，再通过频率变换将低通滤波器转换成其他类型模拟滤波器。

我们考虑因果系统：

H_a(j\Omega)=\int_{0}^{\inf}h_a(t)e^{-j\omega t}dt

其中，h_a(s)是系统的单位脉冲响应，是实函数，那么就有：

H_a(j\Omega)=\int_{0}^{\inf}h_a(t)(\cos \Omega t-j\sin\Omega t)dt

实际上有：H_a(-j\Omega)=H_a^*(j\Omega)

定义模拟滤波器的振幅平方函数为：

A(\Omega^2)=|H_a(j\Omega)|^2=H_a(j\Omega)H_a^*(j\Omega)

令：s=j\Omega

如果要系统稳定，那么A(\Omega^2)=A(-s^2)

如果我们要让系统函数稳定，就应该选用A(-s^2)在s剖面的左半平面的极点作为H_a(s)的极点。

来看看今天的内容：

目录

1、巴特沃斯滤波器

 2、切比雪夫I型滤波器

 3、切比雪夫II型滤波器

 4、椭圆滤波器（考尔滤波器）

 5、低通到低通的频带变换

首先，和Jupyter笔记本一样，先导入我们需要的包：

import numpy as np
import matplotlib.pyplot as plt
import scipy.signal as signal

1、巴特沃斯滤波器

其振幅平方函数为：

A(\Omega)=|H_a(j\Omega)|^2=\frac{1}{1+(\frac{j\Omega}{j\Omega_c})^{2N}}=\frac{1}{1+(\Omega/\Omega_c)^{2N}}

其中，N是滤波器的阶数，N越大，带通和傣族的近似性越好，过渡带也就越陡。

tips：之前一大段时间没有更新，一个是野外没条件，另一个原因就是懒得没有好好去读Scipy.signal的文档，所以说博客有一大段时间空下来了，其实这两天再去读文档，同时对照着Matlab书里面的函数讲解，发现很多都是一样的。

MATLAB中，buttap函数用来计算N阶巴特沃斯归一化，模拟低通原型滤波器系统函数的零点、极点、增益因子的，Python也一样，返回的都是z，p，k，分别是G(p)的极点、零点、增益

我们来看一个最简单的例子：产生一个20阶低通模拟滤波器原型，表示为零极点增益形式：

[z,p,k]=signal.buttap(20)
[n,den]=signal.zpk2tf(z,p,k)
[h,w]=signal.freqs(n,den)
plt.subplot(211)
plt.plot(np.abs(h))
plt.grid(True)
plt.subplot(212)
plt.plot(w)
plt.grid(True)

来看看结果：chule

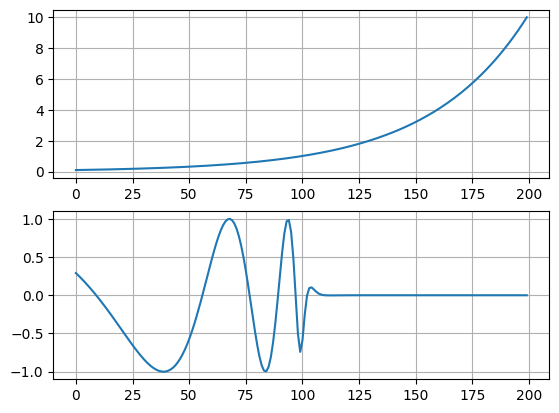
 说实话，除了这张图以外，其他的我都能和Matlab的对的上。

那就来看一看不同阶数下的巴特沃斯滤波器的幅频响应曲线：

n=np.linspace(0,2,200,dtype='float')
[z1,p1,k1]=signal.buttap(1)
[num1,den1]=signal.zpk2tf(z1,p1,k1)
[w1,h1]=signal.freqs(num1,den1)
magh1=abs(h1)
[z2,p2,k2]=signal.buttap(3)
[num2,den2]=signal.zpk2tf(z2,p2,k2)
[w2,h2]=signal.freqs(num2,den2)
magh2=abs(h2)
[z3,p3,k3]=signal.buttap(8)
[num3,den3]=signal.zpk2tf(z3,p3,k3)
[w3,h3]=signal.freqs(num3,den3)
magh3=abs(h3)
[z,p,k]=signal.buttap(12)
[num,den]=signal.zpk2tf(z,p,k)
[w,h]=signal.freqs(num,den)
magh=abs(h)
plt.subplot(2,2,1)
plt.plot(magh1)
plt.grid(True)
plt.subplot(2,2,2)
plt.plot(magh2)
plt.grid(True)
plt.subplot(2,2,3)
plt.plot(magh3)
plt.grid(True)
plt.subplot(2,2,4)
plt.plot(magh)
plt.grid(True)

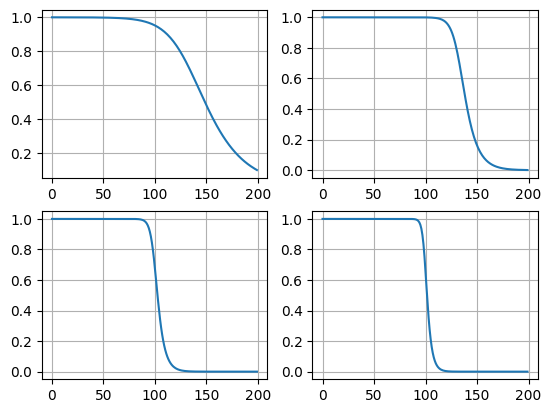
 在已知设计参数\omega_p,\omega_s,R_p,R_s之后，利用buttord函数可以求出所需要的滤波器的阶数和3dB截止频率：

[n,Wn]=signal.buttord(Wp,Ws,Rp,Rs)

其中：

Wp:带通截止频率

Ws:带阻起始频率

Rp:通带内波动

Rs:阻带内最小衰减

1、低通滤波器：

# 采样速率为10000H在，设计一个低通滤波器，fp=2000Hz，fs=3000H在，Rp=4dB，Rs=30dB
fn=10000
fp=900
fs=600
Rp=3
Rs=20
Wp=(fp/(fn/2))
Ws=fs/(fn/2)
[n,Wn]=signal.buttord(Wp,Ws,Rp,Rs)
[b,a]=signal.butter(n,Wn)
[H,F]=signal.freqz(b,a,1000,8000)
plt.subplot(211)
plt.plot(H,20*np.log10(abs(F)))
plt.xlabel("frequency")
plt.ylabel('altitude')
plt.title("LowPass")
plt.grid(True)
pha=np.angle(F)*180/np.pi
plt.subplot(212)
plt.plot(H,pha)
plt.xlabel("frequency")
plt.ylabel('angle')
plt.grid(True)

这里有个地方注意一下：Matlab和Python的signal.freqs/z两个函数的输出顺序是不同的，Matlab的输出的H和W和Python输出的H的W两者刚好调换了位置。sheshe

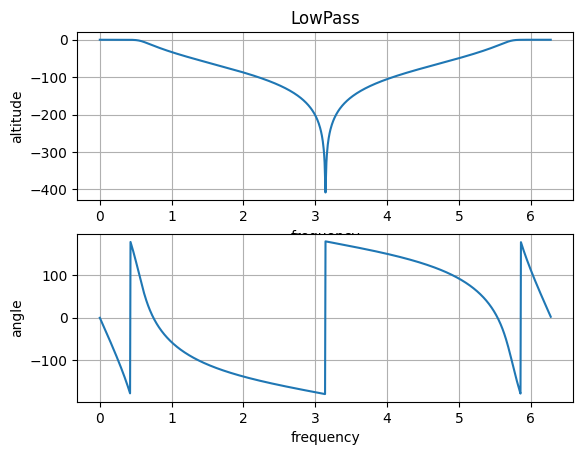
2、高通滤波器：

# 采样速率为10000H在，设计一高通滤波器，fp=900Hz，fs=600Hz，Rp=3dB，Rs=20dB
fn=10000
fp=900
fs=600
Rp=3
Rs=20
Wp=fp/(fn/2)
Ws=fs/(fn/2)
[n,wn]=signal.buttord(Ws,Wp,Rp,Rs)
[b,a]=signal.butter(n,wn,'high')
[H,F]=signal.freqz(b,a,900,10000)
plt.subplot(211)
plt.plot(H,20*np.log10(abs(F)))
plt.xlabel("frequency")
plt.ylabel('altitude')
plt.title("HighPass")
plt.grid(True)
pha=np.angle(F)*180/np.pi
plt.subplot(212)
plt.plot(H,pha)
plt.xlabel("frequency")
plt.ylabel('angle')
plt.grid(True)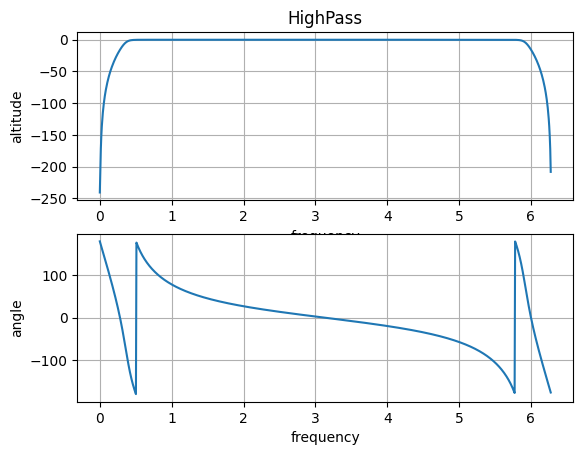

3、带通滤波器：

fn=10000
fp=np.array([600,1700])
fs=np.array([900,1200])
Rp=4
Rs=30
Wp=fp/(fn/2)
Ws=fs/(fn/2)
[n,wn]=signal.buttord(Wp,Ws,Rp,Rs)
[b,a]=signal.butter(n,wn,'bandpass')
[H,F]=signal.freqz(b,a,1000,10000)
plt.subplot(211)
plt.plot(20*np.log10(abs(F)))
plt.xlabel("frequency")
plt.ylabel('altitude')
plt.title("BandPass")
plt.grid(True)
pha=np.angle(F)*180/np.pi
plt.subplot(212)
plt.plot(pha)
plt.xlabel("frequency")
plt.ylabel('angle')
plt.grid(True)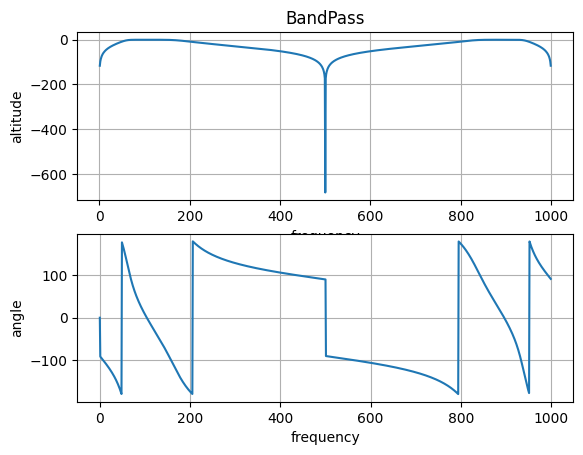

 4、带阻滤波器：

fn=10000
fp=np.array([600,1700])
fs=np.array([900,1200])
Rp=4
Rs=30
Wp=fp/(fn/2)
Ws=fs/(fn/2)
[n,wn]=signal.buttord(Wp,Ws,Rp,Rs)
[b,a]=signal.butter(n,wn,'bandstop')#看到了吗，低通、高通、带通、带阻的选择方式就是这样
[H,F]=signal.freqz(b,a,1000,10000)
plt.subplot(211)
plt.plot(20*np.log10(abs(F)))
plt.xlabel("frequency")
plt.ylabel('altitude')
plt.title("BandPass")
plt.grid(True)
pha=np.angle(F)*180/np.pi
plt.subplot(212)
plt.plot(pha)
plt.xlabel("frequency")
plt.ylabel('angle')
plt.grid(True)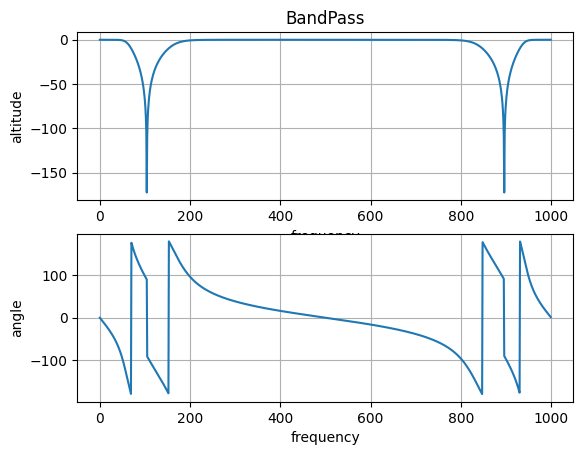

 2、切比雪夫I型滤波器

A(\Omega)=|H_a(j\Omega)|^2=\frac{1}{1+\varepsilon ^2 V_N(\Omega/\Omega_c)}

式中：\Omega_c是有效通带截止频率，\varepsilon是与通带波纹有关的参量，\varepsilon越大，波纹越大，但其范围在(0,1),V_N是N阶切比雪夫多项式：

V_N=\left\{\begin{matrix} & cos(Narccosx),|x|\leqslant 1\\ & cosh(Narcoshx),|x|>1 \end{matrix}\right.

这里就不写Matlab的了，直接写Python的：

[z,p,k]=signal.cheb1ap(N,rs)

n是阶数，rs是通带的幅度误差，返回值分别是滤波器的零点、极点、增益：

Wp=3*np.pi*4*np.power(12,3)
Ws=3*np.pi*12*np.power(10,3)
rp=1
rs=30
wp=1
ws=Ws/Wp
[N,wc]=signal.cheb1ord(Wp,Ws,rp,rs,'lowpass')
[z,p,k]=signal.cheb1ap(N,rs)
[b,a]=signal.zpk2tf(z,p,k)
w=np.linspace(0,np.pi,50,dtype='float')
[h,w1]=signal.freqs(b,a,w)
plt.plot(h*wc/wp,20*np.log10(abs(w1)))
plt.grid(True)

n=np.linspace(0,4,200,dtype='float')
Rp=1
N1=1
N2=3
N3=5
N4=7
[z1,p1,k1]=signal.cheb1ap(N1,Rp)
[b1,a1]=signal.zpk2tf(z1,p1,k1)
[H1,w1]=signal.freqs(b1,a1,n)
magh1=np.power(np.abs(w1),2)
plt.subplot(2,2,1)
plt.plot(H1,magh1)
plt.grid(True)
[z2,p2,k2]=signal.cheb1ap(N2,Rp)
[b2,a2]=signal.zpk2tf(z2,p2,k2)
[H2,w2]=signal.freqs(b2,a2,n)
magh2=np.power(np.abs(w2),2)
plt.subplot(2,2,2)
plt.plot(H2,magh2)
plt.grid(True)
[z3,p3,k3]=signal.cheb1ap(N3,Rp)
[b3,a3]=signal.zpk2tf(z3,p3,k3)
[H3,w3]=signal.freqs(b3,a3,n)
magh3=np.power(np.abs(w3),2)
plt.subplot(2,2,3)
plt.plot(H3,magh3)
plt.grid(True)
[z4,p4,k4]=signal.cheb1ap(N4,Rp)
[b4,a4]=signal.zpk2tf(z4,p4,k4)
[H4,w4]=signal.freqs(b4,a4,n)
magh4=np.power(np.abs(w4),2)
plt.subplot(2,2,4)
plt.plot(H4,magh4)
plt.grid(True)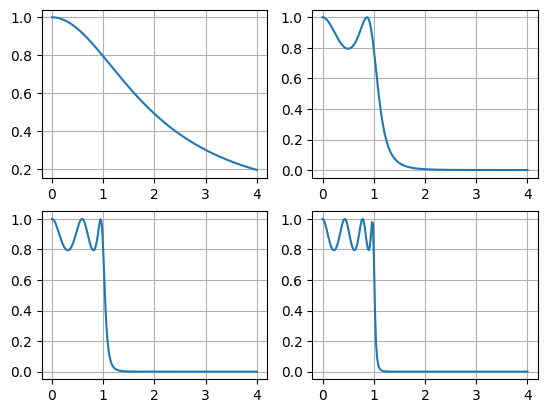

 3、切比雪夫II型滤波器

A(\Omega)=|H_a(j\Omega)|^2=\frac{1}{1+\varepsilon ^2 T^2_N(\Omega/\Omega_c)^{-1}}

[z,p,k]=signal.cheb2ap(N,rs)

n是阶数，rs是通带的波动，返回值分别是滤波器的零点、极点、增益。

Wp=3*np.pi*4*np.power(12,3)
Ws=3*np.pi*12*np.power(10,3)
rp=1
rs=30
wp=1
ws=Ws/Wp
[N,wc]=signal.cheb2ord(wp,ws,rp,rs,'s')
[z,p,k]=signal.cheb2ap(N,rs)
[b,a]=signal.zpk2tf(z,p,k)
w=np.linspace(0,np.pi,50,dtype='float')
[h,w]=signal.freqs(b,a,w)
plt.plot(h*wc/wp,20*np.log10(np.abs(w)))
plt.grid(True)

n=np.linspace(0,4,200,dtype='float')
Rp=1
N1=1
N2=3
N3=5
N4=7
Rp=20
[z1,p1,k1]=signal.cheb2ap(N1,Rp)
[b1,a1]=signal.zpk2tf(z1,p1,k1)
[H1,w1]=signal.freqs(b1,a1,n)
magh1=np.power(np.abs(w1),2)
plt.subplot(2,2,1)
plt.plot(H1,magh1)
plt.grid(True)
[z2,p2,k2]=signal.cheb2ap(N2,Rp)
[b2,a2]=signal.zpk2tf(z2,p2,k2)
[H2,w2]=signal.freqs(b2,a2,n)
magh2=np.power(np.abs(w2),2)
plt.subplot(2,2,2)
plt.plot(H2,magh2)
plt.grid(True)
[z3,p3,k3]=signal.cheb2ap(N3,Rp)
[b3,a3]=signal.zpk2tf(z3,p3,k3)
[H3,w3]=signal.freqs(b3,a3,n)
magh3=np.power(np.abs(w3),2)
plt.subplot(2,2,3)
plt.plot(H3,magh3)
plt.grid(True)
[z4,p4,k4]=signal.cheb2ap(N4,Rp)
[b4,a4]=signal.zpk2tf(z4,p4,k4)
[H4,w4]=signal.freqs(b4,a4,n)
magh4=np.power(np.abs(w4),2)
plt.subplot(2,2,4)
plt.plot(H4,magh4)
plt.grid(True)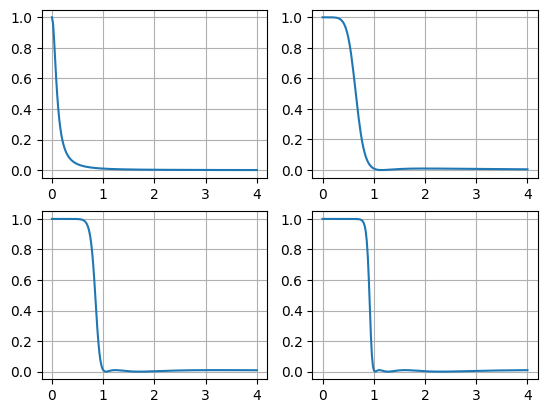

 4、椭圆滤波器（考尔滤波器）

这是一种带通和带阻等波纹的滤波器，在阶数相同的的条件下，有着最小的通和带阻波动，其在带通和带阻的波动相同，特点：

1、是一种零极点型滤波器，在有限频率范围内存在传输零点和极点

2、其通带和阻带都有着等波纹特性，所以通带、阻带逼近特性良好

3、在同样的性能要求下，比前两种滤波器所需要的阶数都低，而且其过渡带比较窄。

A(\Omega)=|H_a(j\Omega)|^2=\frac{1}{1+\varepsilon^2R^2_N(\Omega,L)}

其中，R_N(\Omega,L)是雅各比椭圆函数，L是一个表示波纹性质的参量。

[N,wc]=signal.ellipord(wp,ws,rp,rs)

其功能是求解滤波器的最小阶数，Wp代表通带介质角频率，W是代表阻带起始角频率，Rp表示通带波纹（dB），Rs表示阻带最小衰减（dB）

[z,p,k]=signal.ellipap(N,rp,rs)

同样，求解零点、极点、增益。

Wp=3*np.pi*4*np.power(12,3)
Ws=3*np.pi*12*np.power(10,3)
rp=2
rs=25
wp=1
ws=Ws/Wp
[N,wc]=signal.ellipord(wp,ws,rp,rs,'s')
[z,p,k]=signal.ellipap(N,rp,rs)
[b,a]=signal.zpk2tf(z,p,k)
w=np.linspace(0,2*np.pi,67,dtype='float')
[h,w]=signal.freqs(b,a,w)
plt.plot(h,20*np.log10(np.abs(w)))
plt.grid(True)
plt.axis([0,6.5,-50,0])
plt.show()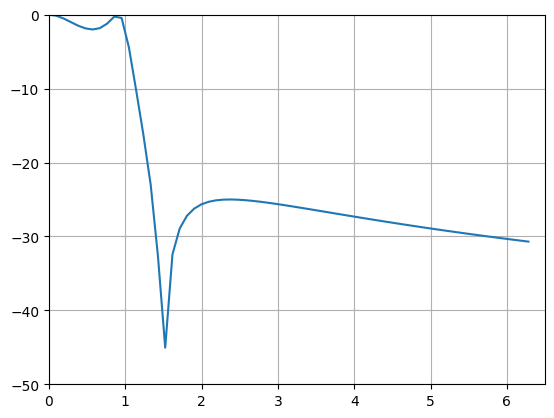

n=np.linspace(0,2,200,dtype='float')
Rp=1
Rs=15
N1=2
N2=3
N3=5
N4=7
[z,p,k]=signal.ellipap(N1,Rp,Rs)
[b,a]=signal.zpk2tf(z,p,k)
[H,w]=signal.freqs(b,a,n)
magh=np.power(np.abs(w),2)
plt.subplot(221)
plt.plot(H,magh)
plt.axis([0,4,0,1])
plt.grid(True)
[z1,p1,k1]=signal.ellipap(N2,Rp,Rs)
[b1,a1]=signal.zpk2tf(z1,p1,k1)
[H1,w1]=signal.freqs(b1,a1,n)
magh1=np.power(np.abs(w1),2)
plt.subplot(222)
plt.plot(H1,magh1)
plt.axis([0,4,0,1])
plt.grid(True)
[z2,p2,k2]=signal.ellipap(N3,Rp,Rs)
[b2,a2]=signal.zpk2tf(z2,p2,k2)
[H2,w2]=signal.freqs(b2,a2,n)
magh2=np.power(np.abs(w2),2)
plt.subplot(223)
plt.plot(H2,magh2)
plt.axis([0,4,0,1])
plt.grid(True)
[z3,p3,k3]=signal.ellipap(N4,Rp,Rs)
[b3,a3]=signal.zpk2tf(z3,p3,k3)
[H3,w3]=signal.freqs(b3,a3,n)
magh3=np.power(np.abs(w3),2)
plt.subplot(224)
plt.plot(H3,magh3)
plt.axis([0,4,0,1])
plt.grid(True)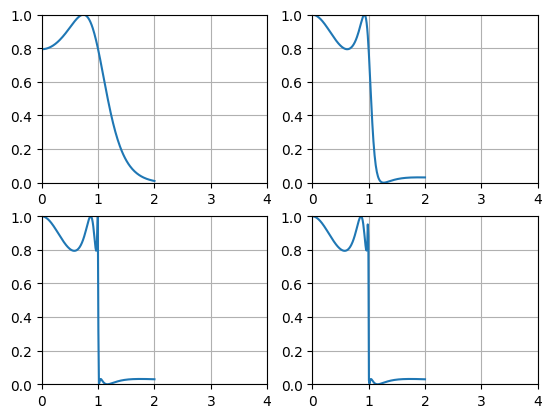

 5、低通到低通的频带变换

[b,a]=signal.lp2lp(bp,ap,Wp)

wp：模拟低通滤波器的通带截止频率

ap：归一化模拟低通滤波器的分子

bp：归一化模拟低通滤波器的分母

a：频带变换后系统函数的分子

b：频带变换后系统函数的分母

来看一个合适的切比雪夫I型滤波器，以实现低通到低通的频带变换

Wp=3*np.pi*5000
Ws=3*np.pi*13000
rp=2
rs=25
wp=1
ws=Ws/Wp
[n,wc]=signal.cheb1ord(wp,ws,rp,rs,'s')
[z,p,k]=signal.cheb1ap(n,wc)
[bp,ap]=signal.zpk2tf(z,p,k)
[b,a]=signal.lp2lp(bp,ap,Wp)
w=np.linspace(0,3*np.pi*30000,250,dtype='float')
[h,w]=signal.freqs(b,a,w)
plt.plot(h/(2*np.pi),20*np.log10(np.abs(w)))
plt.grid(True)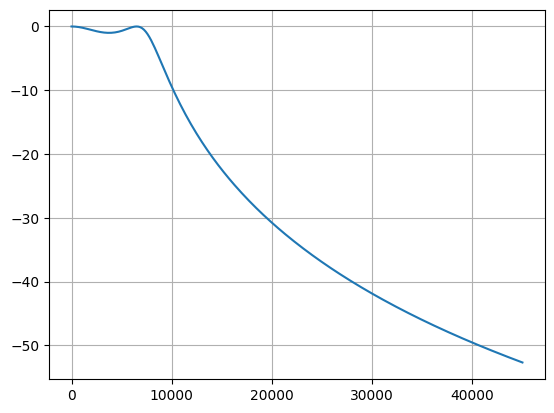

 好了，今天大概就看了这么多，后面的还多着呢，明天再说。

相关文章：

模拟滤波器的基础知识和设计

信号处理工作中滤波器的应用是非常广泛的，可以分成模拟滤波器和数字滤波器两种，数字滤波器主要包括两种，IIR和FIR，这两种滤波器后面统一说，今天先来说一说模拟滤波器（主要是我先用Python实现了Matlab书里面…...

编程日记 2023/10/8 0:56:11

机器学习基础-Pandas学习笔记

Pandas Python的数据分析库，与Numpy配合使用，可以从常见的格式如CSV、JSON等中读取数据。可以进行数据清洗、数据加工工作。数据结构Series，Pandas.Series(data,index,dtype,name,copy) data类型是Numpy的ndarray类型，index指定下…...

编程日记 2023/10/8 0:54:08

【GIT版本控制】--协作流程

一、Fork与Pull Request Git协作流程中的关键概念包括Fork和Pull Request，它们允许多人在项目中协作并贡献代码。以下是关于Fork和Pull Request的简要总结： 1. Fork： Fork是指复制一个Git仓库，通常是一个开源项目的仓库&#xf…...

编程日记 2023/10/8 0:53:07

简析Cookie、Session、Token

手打不易，如果转摘，请注明出处！ 注明原文：https://zhangxiaofan.blog.csdn.net/article/details/133498756 文章目录 简析Cookie、Session、Token什么是 Cookie ？什么是 Session ？Cookie 和 Session 到底是…...

编程日记 2023/10/8 0:52:06

加速attention计算的工业标准：flash attention 1和2算法的原理及实现

transformers目前大火，但是对于长序列来说，计算很慢，而且很耗费显存。对于transformer中的self attention计算来说，在时间复杂度上，对于每个位置，模型需要计算它与所有其他位置的相关性，这样的计…...

编程日记 2023/10/8 0:51:05

小程序获取用户手机号

在小程序中获取用户手机号需要以下步骤： 首先需要授权用户手机号，即在小程序中调用 wx.login() 方法获取用户的登录凭证，在回调函数中调用 wx.getUserInfo() 方法获取用户的个人信息，并且设置 withCredentials 参数为 true。 在获…...

编程日记 2023/10/8 0:49:02

Zama的fhEVM：基于全同态加密实现的隐私智能合约

1. 引言 Zama的fhEVM定位为： 基于全同态加密实现的隐私智能合约 解决方案 开源代码见： https://github.com/zama-ai/fhevm（TypeScript Solidity） Zama的fhEVM协议中主要包含： https://github.com/zama-ai/tfhe-…...

编程日记 2023/10/8 0:45:59

Mac M1安装ROS1或ROS2

1.首先进入Anaconda官网，安装Anaconda 2.创建、激活并配置环境 #创建环境 conda create -n ROS #激活环境 conda activate ROS #配置环境 conda config --add channels conda-forge conda config --add channels robostack conda config --set channel_priority st…...

编程日记 2023/10/8 0:44:58

[NISACTF 2022]popchains - 反序列化+伪协议

[NISACTF 2022]popchains 一、解题流程二、小小疑惑 一、解题流程 1、链条：Road_is_Long（construct->wakeup【page$r】-> toString【string$m】）-> Make_a_Change（construct->get【effort$t】）-> Try_W…...

编程日记 2023/10/8 0:43:57

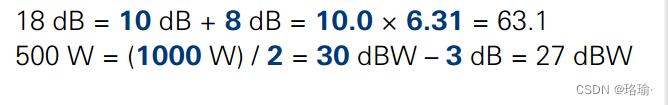
分贝定义简介

一、什么是分贝 辅助单元Bel表示任何给定部件、电路或系统的输入和输出之间的对数比L，并且可以用电压、电流或功率来表示： 如果使用场量（电压或电流）代替功率量，则： 我们可以将增益或损耗因子相加为正或负dB值，而不是将其乘以比率。 分贝与功率转化的速读表如下所示：…...

编程日记 2023/10/8 0:42:56

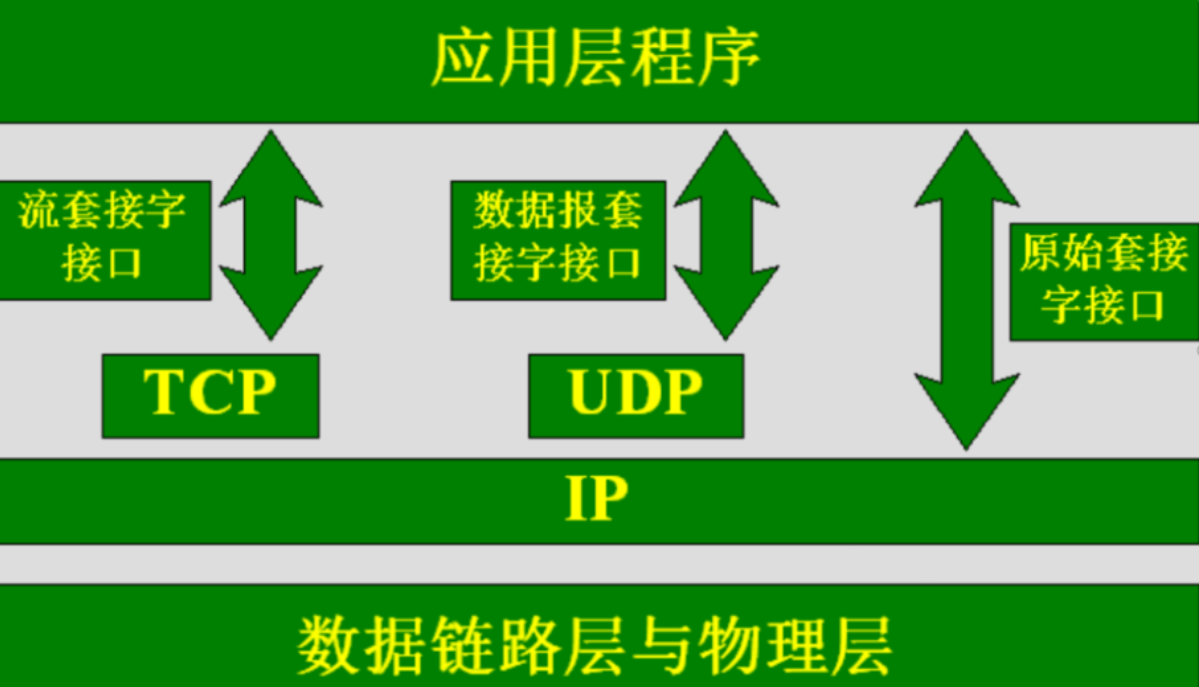
socket简介

套接字（Socket）实质上就是对网络中不同主机上的应用进程之间进行双向通信的端点的抽象。一个套接字就是网络上进程通信的一端，为应用层进程利网络协议交换数据提供了相应机制。套接字出于承上启下的作用，向上连接应用进程&#xf…...

编程日记 2023/10/8 0:41:55

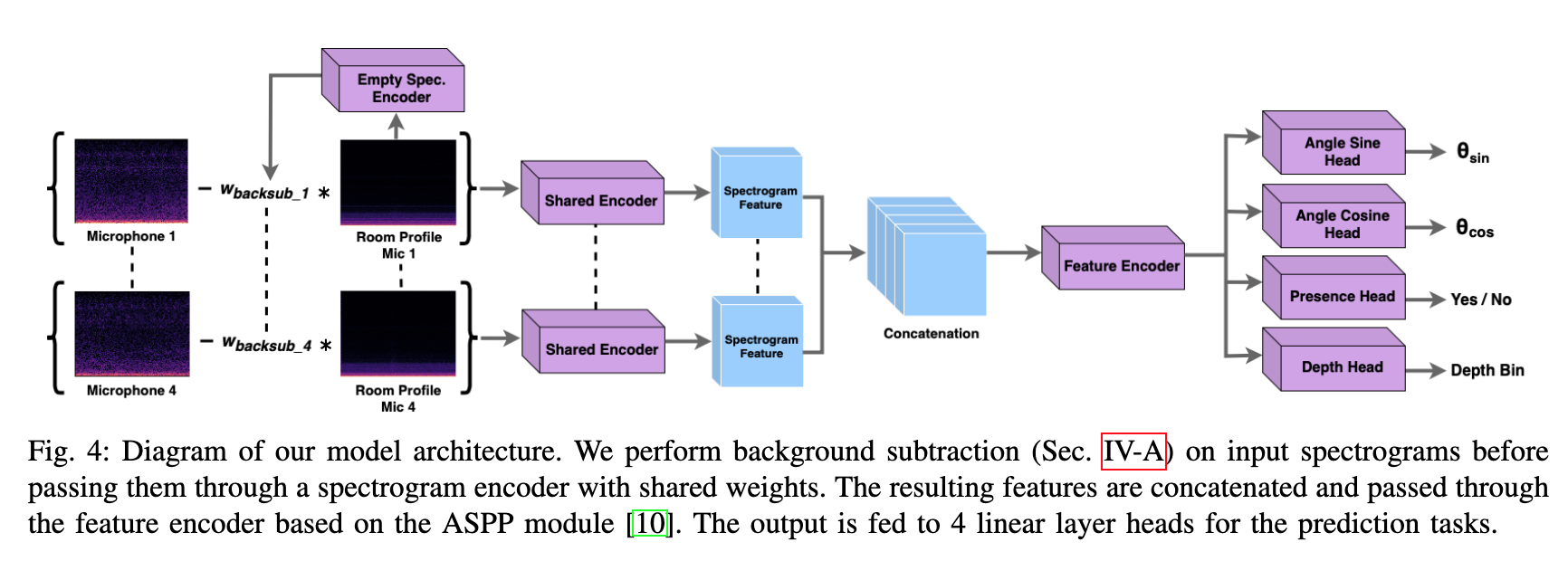
【AI视野·今日Robot 机器人论文速览 第四十九期】Fri, 6 Oct 2023

AI视野今日CS.Robotics 机器人学论文速览 Fri, 6 Oct 2023 Totally 29 papers 👉上期速览✈更多精彩请移步主页 Interesting: 📚ContactGen, 基于生成模型的抓取手势生成，类人五指手。(from 伊利诺伊大学 香槟) 数据集：GRAB da…...

编程日记 2023/10/8 0:40:55

七、互联网技术——SQL查询

文章目录 一、基础查询二、高级查询三、SQL视图一、基础查询 某学校的教学信息关系数据库中有如下两个表(表的名字和字段均用中文名字)学生表(学号，姓名，性别，专业)成绩表(学号，课程名，分数)用SQL语句表达下述查询:[问题1]检索分数高于80分的所有学生的学号和分数select 学…...

编程日记 2023/10/8 0:39:53

1.6 计算机网络的性能

思维导图： 1.6.1 计算机网络的性能指标 前言： 我的理解： 这段前言主要介绍了关于计算机网络性能的两个方面的讨论。首先，计算机网络的性能可以通过一些重要的性能指标来衡量。但除了这些指标之外，还有一些非性能特征…...

编程日记 2023/10/8 0:38:51

小程序中如何核销订单和优惠券

小程序已成为许多商家线上线下开展业务的重要渠道。客户在小程序中下单/领券后，可能需要商家现场扫码核销，例如超市购物、卖票、游乐园等线下场景。下面就介绍小程序中如何核销订单和优惠券。 一、订单核销 订单核销是指商家在小程序中确认顾客已经支付…...

编程日记 2023/10/8 0:36:48

211 毕业就入职 30 人的小公司是什么体验

为什么“选择”了 30 人的小公司？ 作为一个 211 毕业的学生，进入 30 人的小公司不管是 8 年前还是现在，应该都是比较稀少的，但是当面的我阴差阳错进了这样一个小公司。 为什么我选择进入这样一个 30 人的小公司呢？主…...

编程日记 2023/10/8 0:34:46

aardio 读取 Excel文件，显示在 listview 中

编写 main.aardio 如下 import win.ui; /*DSG{{*/ winform win.form(text"excel1";right801;bottom500) winform.add( button1{cls"button";text"读取Excel文件";left19;top14;right126;bottom44;z1}; button2{cls"button";text&quo…...

编程日记 2023/10/8 0:33:45

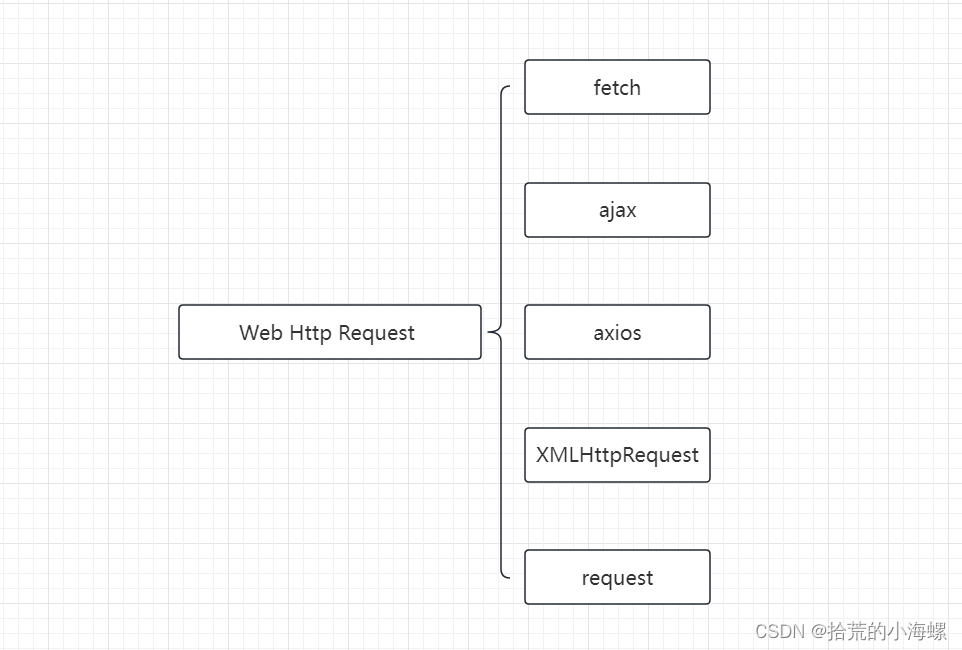
Web：前端常用的几种Http请求GET和POST样例

1、简述 在Web开发过程中，少不了发起Http请求服务端的接口数据，在不同的框架中使用了不同的Http请求方式，常用的请求有fetch、 ajax、 axios、XMLHttpRequest、request，以下样例仅供参考。 2、Fetch Fetch API 是一种 JavaScr…...

编程日记 2023/10/8 0:31:44

clickonce 发布的winform 如何CA认证？

要为使用ClickOnce发布的WinForms应用程序启用CA（证书颁发机构）认证，您可以按照以下步骤进行操作： 1. **获取数字证书**： - 首先，您需要获得一个数字证书，通常从受信任的CA购买。这个数字证…...

编程日记 2023/10/8 0:29:42

#力扣：13. 罗马数字转整数@FDDLC

13. 罗马数字转整数 一、Java import java.util.HashMap;class Solution {public int romanToInt(String s) {HashMap<Character, Integer> m new HashMap<>() {{put(I, 1);put(V, 5);put(X, 10);put(L, 50);put(C, 100);put(D, 500);put(M, 1000);}};char[] a …...

编程日记 2023/10/8 0:28:41

连锁超市冷库节能解决方案：如何实现超市降本增效

在连锁超市冷库运营中&#xff0c;高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术&#xff0c;实现年省电费15%-60%&#xff0c;且不改动原有装备、安装快捷、…...

编程新知 2025/6/25 0:28:07

CocosCreator 之 JavaScript/TypeScript和Java的相互交互

引擎版本&#xff1a; 3.8.1 语言&#xff1a; JavaScript/TypeScript、C、Java 环境&#xff1a;Window 参考&#xff1a;Java原生反射机制 您好&#xff0c;我是鹤九日&#xff01; 回顾 在上篇文章中&#xff1a;CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

编程新知 2025/6/20 11:32:51

c#开发AI模型对话

AI模型 前面已经介绍了一般AI模型本地部署&#xff0c;直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型&#xff0c;但是目前国内可能使用不多&#xff0c;至少实践例子很少看见。开发训练模型就不介绍了&am…...

编程新知 2025/6/26 5:40:36

Java面试专项一-准备篇

一、企业简历筛选规则 一般企业的简历筛选流程&#xff1a;首先由HR先筛选一部分简历后&#xff0c;在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如&#xff1a;Boss直聘&#xff08;招聘方平台&#xff09; 直接按照条件进行筛选 例如&#xff1a…...

编程新知 2025/7/2 15:01:02

算法岗面试经验分享-大模型篇

文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer &#xff08;1&#xff09;资源 论文&a…...

编程新知 2025/6/26 5:09:05

MySQL 部分重点知识篇

一、数据库对象 1. 主键 定义 &#xff1a;主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 &#xff1a;确保数据的完整性&#xff0c;便于数据的查询和管理。 示例 &#xff1a;在学生信息表中&#xff0c;学号可以作为主键&#xff…...

编程新知 2025/6/21 8:31:44

第7篇：中间件全链路监控与 SQL 性能分析实践

7.1 章节导读 在构建数据库中间件的过程中&#xff0c;可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中&#xff0c;必须做到&#xff1a; &#x1f50d; 追踪每一条 SQL 的生命周期&#xff08;从入口到数据库执行&#xff09;&#…...

编程新知 2025/6/26 23:27:47

libfmt: 现代C++的格式化工具库介绍与酷炫功能

libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库&#xff0c;提供了高效、安全的文本格式化功能&#xff0c;是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全&#xff1a…...

编程新知 2025/6/13 5:38:47

抽象类和接口（全）

一、抽象类 1.概念&#xff1a;如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象&#xff0c;这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法&#xff0c;包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中&#xff0c;⼀个类如果被 abs…...

编程新知 2025/6/21 12:42:46

离线语音识别方案分析

随着人工智能技术的不断发展&#xff0c;语音识别技术也得到了广泛的应用&#xff0c;从智能家居到车载系统&#xff0c;语音识别正在改变我们与设备的交互方式。尤其是离线语音识别&#xff0c;由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力&#xff0c;广…...

编程新知 2025/6/20 13:59:53