经典算法----迷宫问题(找出所有路径)
目录
前言
问题描述
算法思路
定义方向
回溯算法
代码实现
前言
前面我发布了一篇关于迷宫问题的解决方法,是通过栈的方式来解决这个问题的(链接:经典算法-----迷宫问题(栈的应用)-CSDN博客),但是这个方法只可以找到一条路径,那么今天我们就进一步去讲解迷宫问题,通过回溯算法来找到全部的路径,下面就一起来看看吧!
问题描述
给定一个迷宫,指明起点和终点,找出从起点出发到终点的有效可行路径,就是迷宫问题(maze problem)。迷宫可以以二维数组来存储表示。0表示通路,1表示障碍。注意这里规定移动可以从上、下、左、右四方方向移动,求走出迷宫的全部路径
#define m 4
#define n 4int maze[m + 2][n + 2] = {{1, 1, 1, 1, 1, 1},{1, 0, 0, 0, 1, 1},{1, 0, 1, 0, 0, 1},{1, 0, 0, 0, 1 ,1},{1, 1, 0, 0, 0, 1},{1, 1, 1, 1, 1, 1}};
算法思路
定义方向
同样的,每走到一个位置就要想该往哪一个方向去走,所以有东南西北这4个方向,每次往一个方向走之后就标记好当前方向和当前位置,然后同样的去进行分享的试探,当走到没路走的时候就进行原路返回。方向的定义如下:
//试探方向存储结构
typedef struct {int xx, yy;
}Direction;
//东南西北
Direction dire[4] = { {0,1},{1,0},{0,-1},{-1,0} };回溯算法
回溯,计算机算法,回溯法也称试探法,它的基本思想是:从问题的某一种状态(初始状态)出发,搜索从这种状态出发所能达到的所有“状态”,当一条路走到“尽头”的时候(不能再前进),再后退一步或若干步,从另一种可能“状态”出发,继续搜索,直到所有的“路径”(状态)都试探过。这种不断“前进”、不断“回溯”寻找解的方法,就称作“回溯法”。递归回溯:由于回溯法是对解空间的深度优先搜索,找到结果或者没找到结果就原路返回去找下一条路。可以看出回溯算法是一种暴力算法,就是彻彻底底的一个一个找,找得到就走,找不到就回去。
对于本期的迷宫问题,我们要想找到全部的路径,就最好去用回溯算法,也就是一个一个找,毕竟实际情况走迷宫也是如此,在不知道的情况下,也只能去一个一个找。对于本题,我们可以这样子走,每走一个地方就把这个地方标记为-1,表示已经走过,当遇到死路的时候,就返回上一个位置,然后换一个方向来走,直到换到可以走得通的方向,走完这条路的话(当前走完的路所有坐标都标记为-1),我们就一直回溯换方向到其他方向能走的位置,直到整个地图全部能走的路都标记为-1,就结束回溯递归。
代码实现
#include<stdio.h>
#define m 4
#define n 4//试探方向存储结构
typedef struct {int xx, yy;
}Direction;
//东南西北
Direction dire[4] = { {0,1},{1,0},{0,-1},{-1,0} };typedef struct node {int x, y;
}Node;
typedef struct path {Node data[100];//标记路径位置的数组int count;//统计节点
}Path;//输出路径
void print(Path p, int* N) {*N += 1;printf("第%d条路径:\n", *N);for (int i = 0; i < p.count; i++) {printf("(%d,%d)->", p.data[i].x, p.data[i].y);}printf("Printover!\n\n");
}void find_path(int maze[][n+2], int* N, int x, int y, int endx, int endy, Path p) {//如果走到终点的时候if (x == endx && y == endy) {maze[x][y] = -1;//把终点位置存入到路径去p.data[p.count].x = x;p.data[p.count].y = y;p.count++;print(p, N);//输出路径//走完了就回到上一个位置,然后换方向走return;}else {//如果当前位置为0,也就是能走的话if (maze[x][y] == 0) {int di = 0;while (di < 4) {//4个方向都进行试探//储存当前位置p.data[p.count].x = x;p.data[p.count].y = y;p.count++;//标记为-1,表示已经走过maze[x][y] = -1;int i, j;//改变方向i = x + dire[di].xx;j = y + dire[di].yy;find_path(maze, N, i, j, endx, endy, p);//递归进入到下一个位置//回溯:回到上一个位置继续操作//当前位置给抹除掉p.count--;maze[x][y] = 0;di++;//改变方向}}//不能走的话就返回,回到上一个位置elsereturn;}
}int main() {int maze[m + 2][n + 2] = {{1, 1, 1, 1, 1, 1},{1, 0, 0, 0, 1, 1},{1, 0, 1, 0, 0, 1},{1, 0, 0, 0, 1 ,1},{1, 1, 0, 0, 0, 1},{1, 1, 1, 1, 1, 1}};Path mp;mp.count = 0;int N = 0;find_path(maze, &N, 1, 1, m, n, mp);
}结果如下:
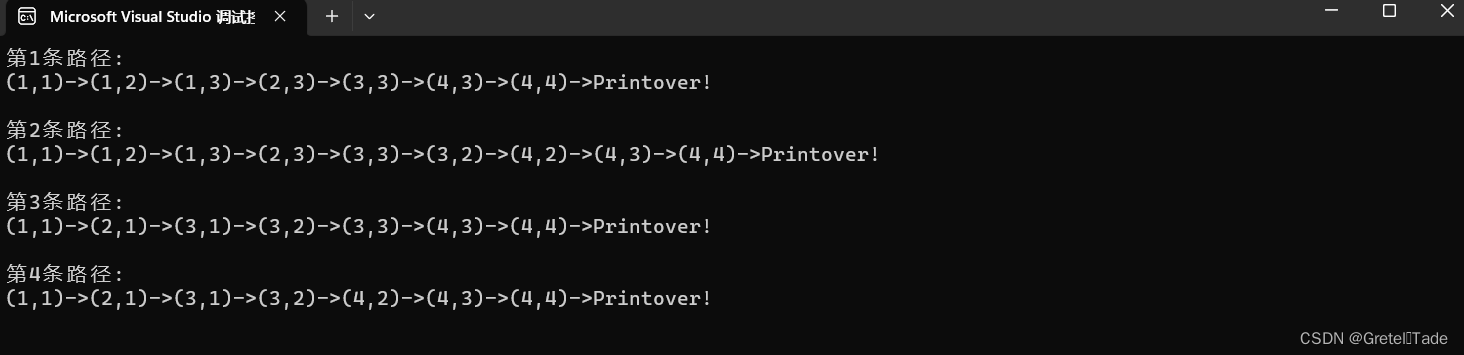
以上就是本期的全部内容了,我们下次见!
分享一张壁纸: 
相关文章:

经典算法----迷宫问题(找出所有路径)
目录 前言 问题描述 算法思路 定义方向 回溯算法 代码实现 前言 前面我发布了一篇关于迷宫问题的解决方法,是通过栈的方式来解决这个问题的(链接:经典算法-----迷宫问题(栈的应用)-CSDN博客)ÿ…...

macOS下 /etc/hosts 文件权限问题修复方案
文章目录 前言解决方案权限验证 macOS下 etc/hosts 文件权限问题修复 前言 当在 macOS 上使用 vi编辑 /etc/hosts 文件时发现出现 Permission Denied 的提示,就算在前面加上 sudo 也照样出现一样的提示,解决方案如下; 解决方案 可以尝试使用如下命令尝试解除锁定; sudo chf…...
 playbook)
【星海出品】ansible入门(二) playbook
核心是管理配置进行批量节点部署。 执行其中的一些列tasks。 playbook由YAML语言编写。 YAML的格式如下: 文件名应该以 .yml 结尾 1.文件的第一行应该以“—”(三个连字符)开始,表明YAML文件的开始。 2.在同一行中,#之…...

Spring Boot对账号密码进行加密储存
未来避免明文硬编码,我们需要对密码进行加密保存,例如账号密码 方法 在Spring Boot中,可以使用Jasypt(Java Simplified Encryption)库来对敏感信息进行加密和解密。Jasypt提供了一种简单的方式来在应用程序中使用加密…...

总结js中常见的层次选择器
js中的层次选择器可以用于选择和操作DOM树中的元素,根据元素的层级关系进行选择。以下是js中常见的层次选择器: 1. getElementById:使用元素的ID属性进行选择。通过给元素设置唯一的ID属性,可以使用getElementById方法选择该元素…...
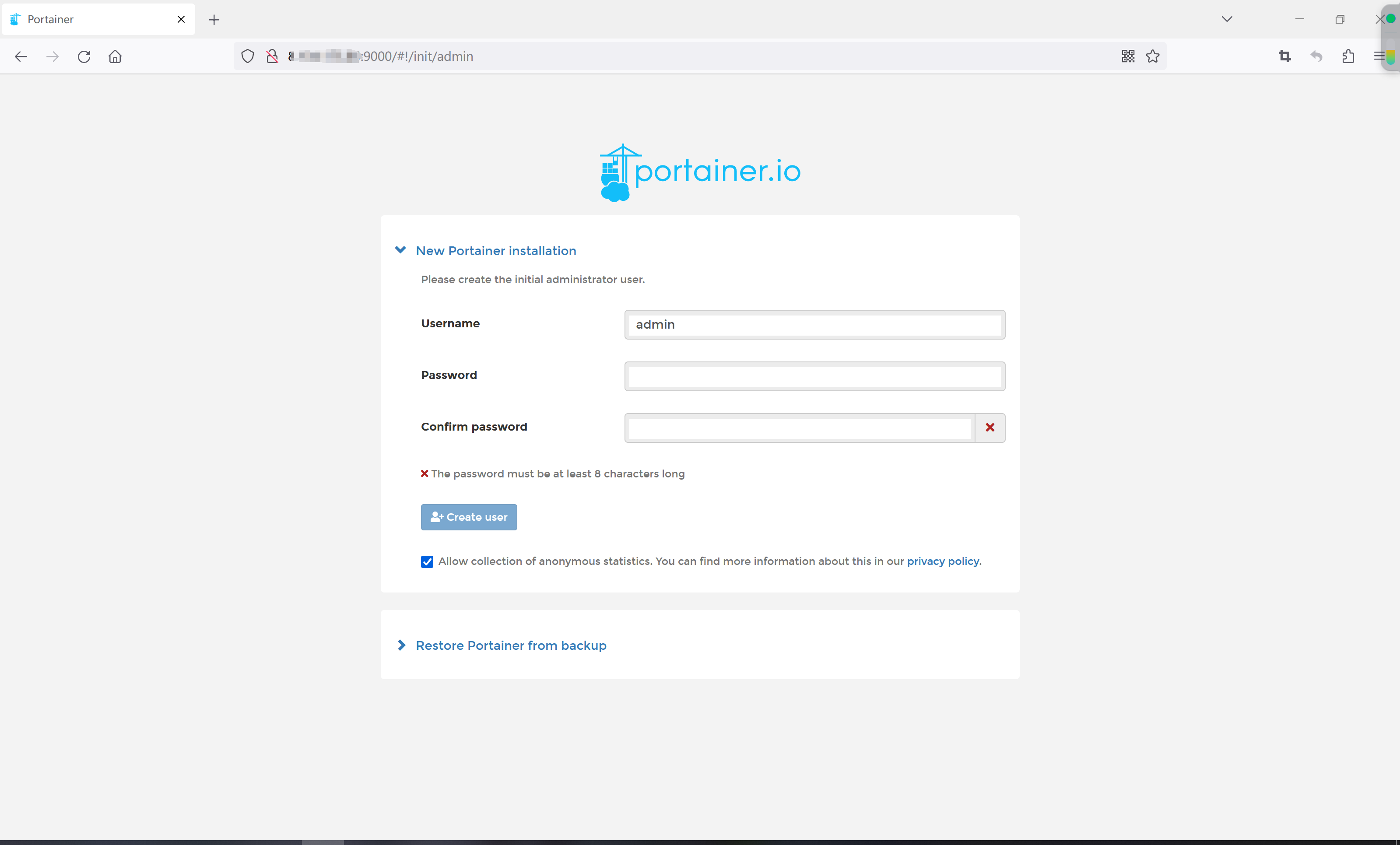
阿里云ECS服务器上启动的portainer无法访问的问题
如下图,在阿里云ECS服务器上安装并启动了portainer,但是在自己电脑上访问不了远程的portainer。 最后发现是要在网络安全组里开放9000端口号,具体操作如下: 在云服务器管理控制台点击左侧菜单中的网络与安全-安全组,然…...

JavaScript系列从入门到精通系列第十八篇:JavaScript中的函数作用域
文章目录 前言 一:函数作用域 前言 我们刚才提到了,在<Script>标签当中进行定义的变量、对象、函数对象都属于全局作用域,全局作用域在页面打开的时候生效在页面关闭的时候失效。 一:函数作用域 调用函数时创建函数作用域…...
开环模块化多电平换流器仿真(MMC)N=6(Simulink仿真)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
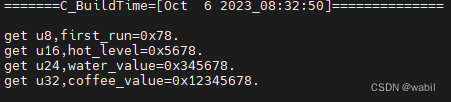
[C]嵌入式中变量存储方案
#include<stdio.h>#define uint8_t unsigned char #define uint16_t unsigned short #define uint24_t unsigned int #define uint32_t unsigned int #define uint64_t unsigned long long//用户自定义变量名字,用于存储 typedef enum {first_run 0,//…...
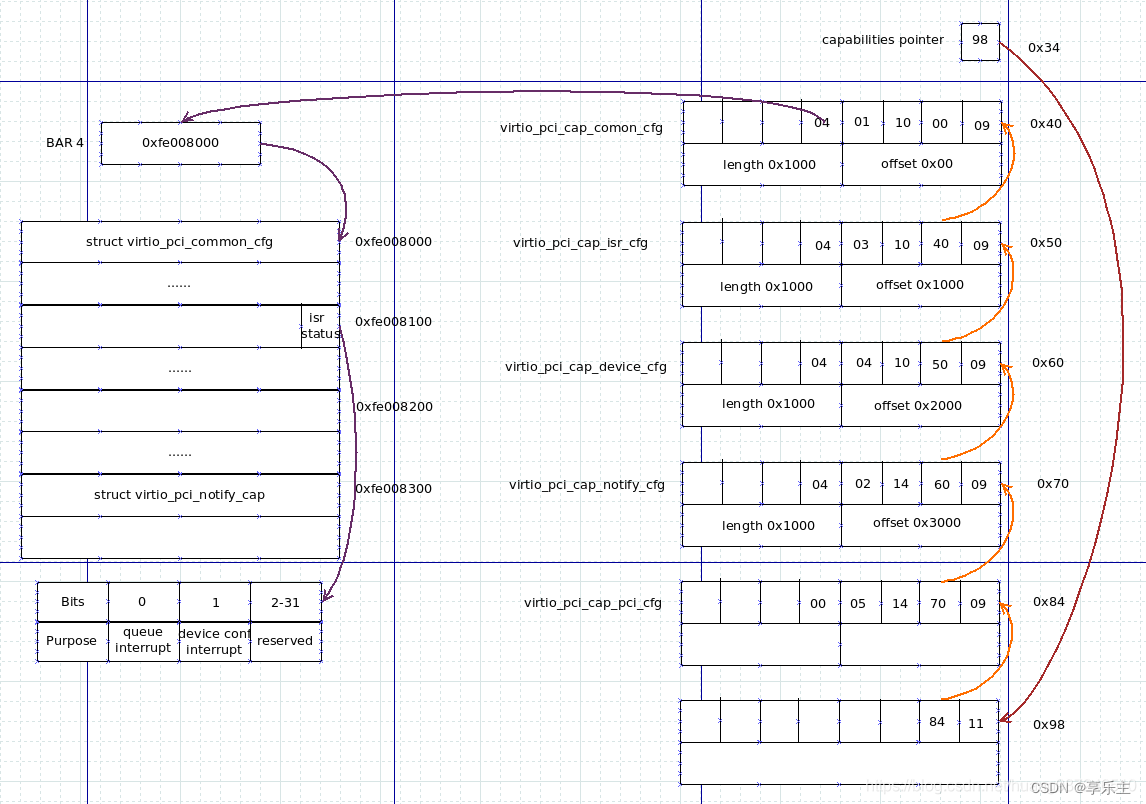
热迁移中VirtIO-PCI设备的配置空间处理
文章目录 问题现象定位过程日志分析源端目的端 原理分析基本原理上下文分析复现分析patch分析 总结解决方案 问题现象 集群升级虚拟化组件版本,升级前存量运行并挂载了virtio磁盘的虚拟机集群内热迁移到升级后的节点失败,QEMU报错如下: 202…...
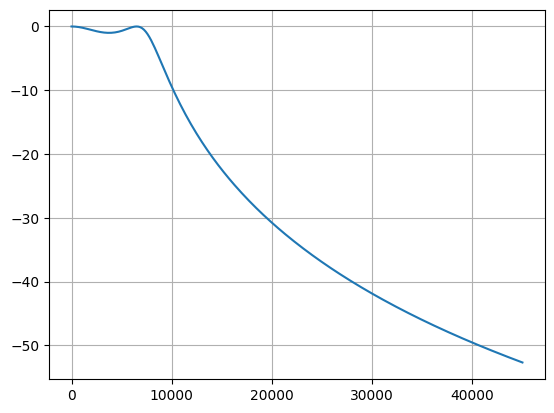
模拟滤波器的基础知识和设计
信号处理工作中滤波器的应用是非常广泛的,可以分成模拟滤波器和数字滤波器两种,数字滤波器主要包括两种,IIR和FIR,这两种滤波器后面统一说,今天先来说一说模拟滤波器(主要是我先用Python实现了Matlab书里面…...

机器学习基础-Pandas学习笔记
Pandas Python的数据分析库,与Numpy配合使用,可以从常见的格式如CSV、JSON等中读取数据。可以进行数据清洗、数据加工工作。数据结构Series,Pandas.Series(data,index,dtype,name,copy) data类型是Numpy的ndarray类型,index指定下…...

【GIT版本控制】--协作流程
一、Fork与Pull Request Git协作流程中的关键概念包括Fork和Pull Request,它们允许多人在项目中协作并贡献代码。以下是关于Fork和Pull Request的简要总结: 1. Fork: Fork是指复制一个Git仓库,通常是一个开源项目的仓库…...

简析Cookie、Session、Token
手打不易,如果转摘,请注明出处! 注明原文:https://zhangxiaofan.blog.csdn.net/article/details/133498756 文章目录 简析Cookie、Session、Token什么是 Cookie ?什么是 Session ?Cookie 和 Session 到底是…...

加速attention计算的工业标准:flash attention 1和2算法的原理及实现
transformers目前大火,但是对于长序列来说,计算很慢,而且很耗费显存。对于transformer中的self attention计算来说,在时间复杂度上,对于每个位置,模型需要计算它与所有其他位置的相关性,这样的计…...

小程序获取用户手机号
在小程序中获取用户手机号需要以下步骤: 首先需要授权用户手机号,即在小程序中调用 wx.login() 方法获取用户的登录凭证,在回调函数中调用 wx.getUserInfo() 方法获取用户的个人信息,并且设置 withCredentials 参数为 true。 在获…...

Zama的fhEVM:基于全同态加密实现的隐私智能合约
1. 引言 Zama的fhEVM定位为: 基于全同态加密实现的隐私智能合约 解决方案 开源代码见: https://github.com/zama-ai/fhevm(TypeScript Solidity) Zama的fhEVM协议中主要包含: https://github.com/zama-ai/tfhe-…...

Mac M1安装ROS1或ROS2
1.首先进入Anaconda官网,安装Anaconda 2.创建、激活并配置环境 #创建环境 conda create -n ROS #激活环境 conda activate ROS #配置环境 conda config --add channels conda-forge conda config --add channels robostack conda config --set channel_priority st…...

[NISACTF 2022]popchains - 反序列化+伪协议
[NISACTF 2022]popchains 一、解题流程二、小小疑惑 一、解题流程 1、链条:Road_is_Long(construct->wakeup【page$r】-> toString【string$m】)-> Make_a_Change(construct->get【effort$t】)-> Try_W…...
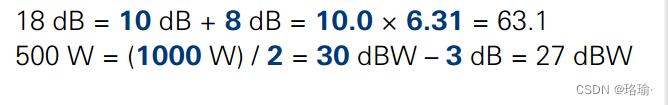
分贝定义简介
一、什么是分贝 辅助单元Bel表示任何给定部件、电路或系统的输入和输出之间的对数比L,并且可以用电压、电流或功率来表示: 如果使用场量(电压或电流)代替功率量,则: 我们可以将增益或损耗因子相加为正或负dB值,而不是将其乘以比率。 分贝与功率转化的速读表如下所示:…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...

GB/T 43887-2024 核级柔性石墨板材检测
核级柔性石墨板材是指以可膨胀石墨为原料、未经改性和增强、用于核工业的核级柔性石墨板材。 GB/T 43887-2024核级柔性石墨板材检测检测指标: 测试项目 测试标准 外观 GB/T 43887 尺寸偏差 GB/T 43887 化学成分 GB/T 43887 密度偏差 GB/T 43887 拉伸强度…...

vxe-table vue 表格复选框多选数据,实现快捷键 Shift 批量选择功能
vxe-table vue 表格复选框多选数据,实现快捷键 Shift 批量选择功能 查看官网:https://vxetable.cn 效果 代码 通过 checkbox-config.isShift 启用批量选中,启用后按住快捷键和鼠标批量选取 <template><div><vxe-grid v-bind"gri…...
