华为OD机试真题Python实现【水仙花数】真题+解题思路+代码（20222023）
相关文章：
华为OD机试真题Python实现【水仙花数】真题+解题思路+代码（20222023）
水仙花数 题目 所谓的水仙花数是指一个n位的正整数其各位数字的n次方的和等于该数本身， 例如153 = 1^3 + 5^3 + 3^3,153是一个三位数 🔥🔥🔥🔥🔥👉👉👉👉👉👉 华为OD机试（Python）真题目录汇总 输入 第一行输入一个整数N， 表示 N 位的正整数 N 在3…...
【华为OD机试模拟题】用 C++ 实现 - 非严格递增连续数字序列（2023.Q1）
最近更新的博客 华为OD机试 - 入栈出栈（C++） | 附带编码思路 【2023】 华为OD机试 - 箱子之形摆放（C++） | 附带编码思路 【2023】 华为OD机试 - 简易内存池 2（C++） | 附带编码思路 【2023】 华为OD机试 - 第 N 个排列（C++） | 附带编码思路 【2023】 华为OD机试 - 考古…...
RN面试题
RN面试题1.React Native相对于原生的ios和Android有哪些优势？1.性能媲美原生APP 2.使用JavaScript编码，只要学习这一种语言 3.绝大部分代码安卓和IOS都能共用 4.组件式开发，代码重用性很高 5.跟编写网页一般，修改代码后即可自动刷…...
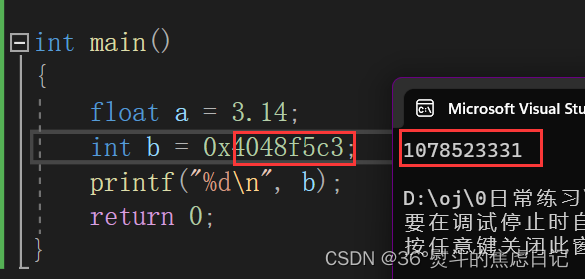
【数据存储】浮点型在内存中的存储
目录 一、存储现象 二、IEEE标准规范 1.存储 2.读取 三、举例验证 1.存储 2.读取 浮点型存储的标准是IEEE（电气电子工程师学会）754制定的。 一、存储现象 浮点数由于其有小数点的特殊性，有很多浮点数是不能精确存储的，如&#…...
Servlet笔记（8）：异常处理
1、错误页面配置 web.xml <!-- servlet 定义 --> <servlet><servlet-name>ErrorHandler</servlet-name><servlet-class>ErrorHandler</servlet-class> </servlet> <!-- servlet 映射 --> <servlet-mapping><servle…...
stm32f407探索者开发板（二十一）——窗口看门狗
文章目录一、窗口看门狗概述1.1 看门狗框图1.2 窗口看门狗工作过程总结1.3 超时时间1.4 为什么需要窗口看门狗1.5 其他注意事项二、常用寄存器和库函数2.1 控制寄存器WWDG_ CR2.2 配置寄存器WWDG_ CFR2.3 状态寄存器WWDG_SR三、手写窗口看门狗3.1 配置过程3.2 初始化窗口看门狗…...
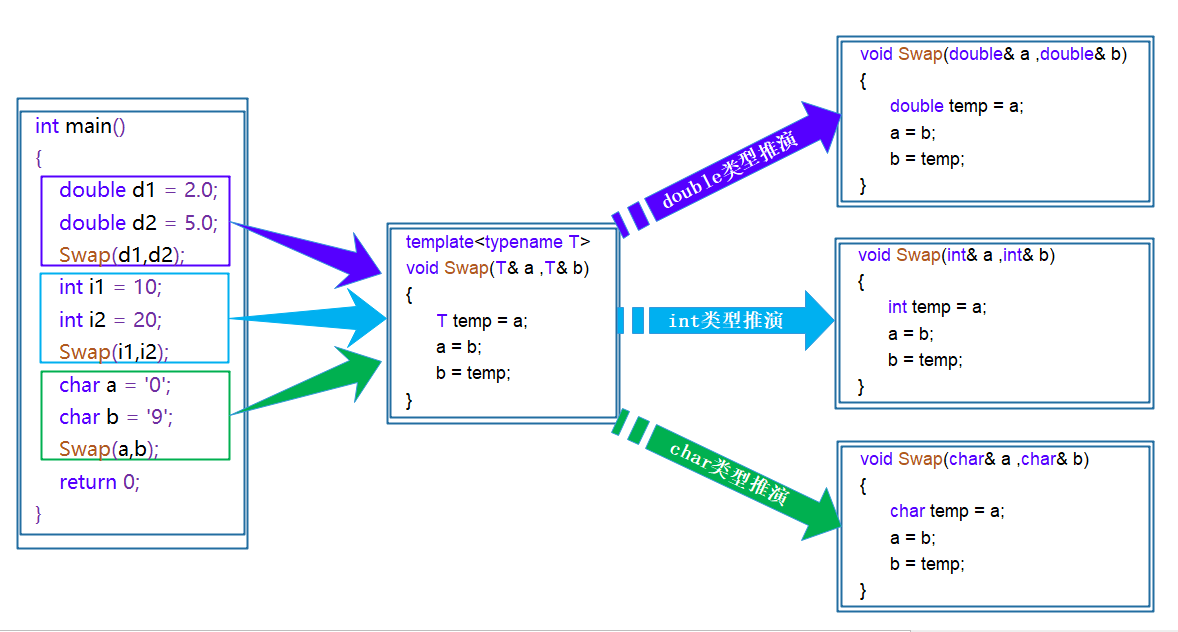
C++ 模板
1. 泛型编程实现一个通用的交换函数，使用函数重载虽然可以实现，但是有以 下几个不好的地方：1. 重载的函数仅仅是类型不同，代码复用率比较低，只要有新类型出现时，就需要用户自己增加对应的函数2. 代码的可维…...
C++中的友元及运算符重载
友元 意义 程序中，有些私有属性也想让类外特殊的一些函数或者类进行访问，就要用到友元技术 关键字 friend 友元的三种实现 全局函数做友元 class Room{friend void test(Person &p);//friend class test;public:string phone_number;private:string…...
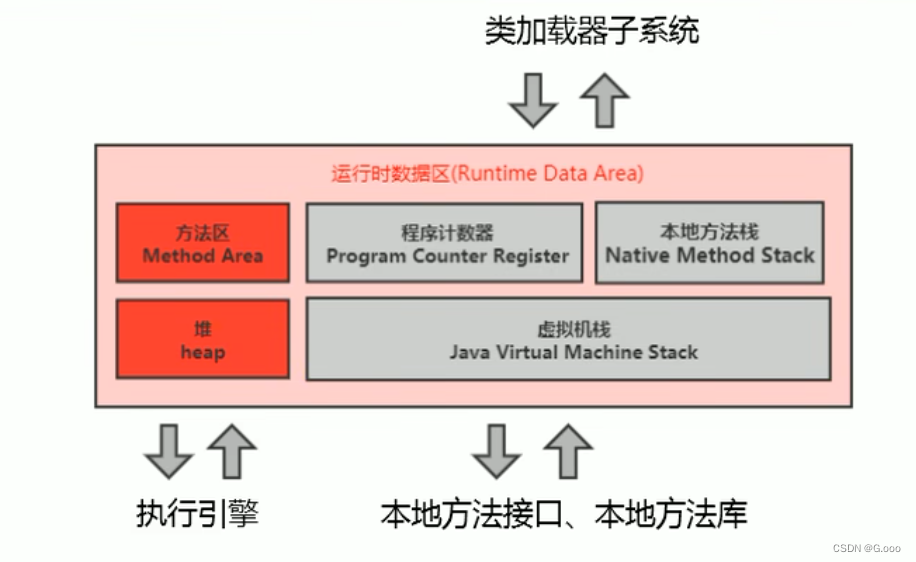
五、运行时数据区内部结构、JVM中的线程
内存是非常重要的系统资源，是硬盘和cpu的中间仓库及桥梁，承载着操作系统和应用程序的实时运行。JVM内存布局规定了Java在运行过程种内存申请、分配‘、管理的策略，保证了JVM的高效稳定运行，不同的JVM对于内存的划分方式和管理机制…...
Codeforces Round #848 (Div. 2)A-C
传送门 目录 A. Flip Flop Sum 代码： B. The Forbidden Permutation 代码： C. Flexible String 代码： A. Flip Flop Sum 题意：给你一个长度为n的数组（数组元素只为1或者-1），你要且只能进行…...
机器学习笔记之近似推断(一)从深度学习角度认识推断
机器学习笔记之近似推断——从深度学习角度认识推断引言推断——基本介绍精确推断难的原因虽然能够表示，但计算代价太大无法直接表示引言 本节是一篇关于推断总结的博客，侧重点在于深度学习模型中的推断任务。 推断——基本介绍 推断(Inference\text{…...
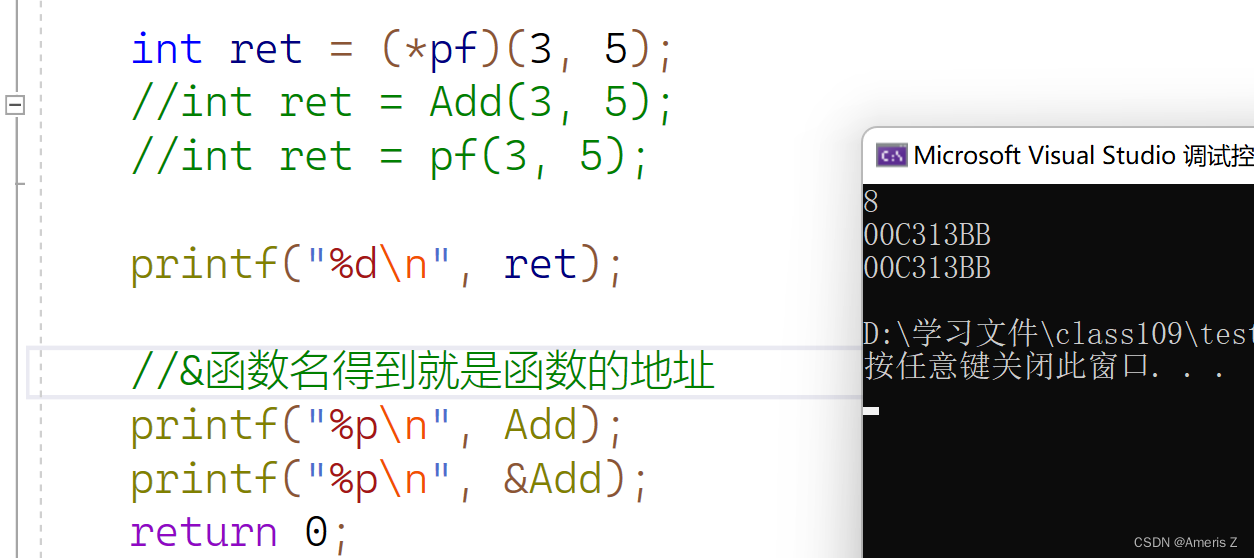
指针的进阶
一、字符指针 int main() {char ch w;char* pc &ch;//pc就是字符指针//const char *p "abcdef";//这里其实是把字符串"abcdef"的首地址放入了指针p中//*p w;//这是错误的无法修改值（可以看到这里绿色波浪线警告）char arr[] …...
一元二次方程方程的类
1 问题设计一个一元二次方程的类，其中包括能够反映一元二次方程的属性与操作行为，然后再设计一个测试类，检测类的使用情况。2 方法使用package语句将方程的属性即计算跟的方法封装在一个有包名的类中，包名为tom.jiafei，…...
Ask林曦｜来回答，30个你关心的日常问题（二）
在林曦老师的线上书法直播课上，上课前后的聊天时间里，时常有同学向林曦老师提问，这些问题涵盖了日常生活的诸多方面，从身体的保养，到快乐的法门，皆是大家感兴趣的，也都共同关切的。 暄桐教室…...
哪款电容笔适合开学季？电容笔和Apple Pencil的区别
其实，市场上一般的电容笔和Apple Pencil的最大差别，就在于Apple Pencil与普通电容笔两者的重量和压感。然而，由于苹果电容笔价格过高，目前电容笔的市场份额逐渐转向平替电容笔，平替电容笔其性能也逐渐得到改善。下面&a…...
Qt之Qprocess
QProcess 可用于完成启动外部程序，并与之交互通信。 一、启动外部程序的两种方式 1）一体式：void QProcess::start(const QString & program,const QStringList &arguments,OpenMode mode ReadWrite) 外部程序启动后&…...
为什么不愿意专升本 学历有什么用
专升本包括两种形式普通专升本和成人专升本。普通专升本毕业是全日制学历，考试仅有一次，错过不能补考所以考生不愿意选择，成人专升本毕业是非全日制学历，学历被国家承认，和普通高校毕业证有相同的使用效力。为何考生不…...
构造函数的使用大全
概述 在C中创建一个对象时，通常需要做一些数据初始化的工作，因此便提供了一个特殊的成员函数 —— 构造函数。一般情况下，并不需要程序员主动调用构造函数，而是在创建对象时，由系统自动调用。构造函数可以由程序员定义…...
ASP.NET Core MVC 项目 IOC容器
目录 一：什么是IOC容器 二：简单理解内置Ioc容器 三：依赖注入内置Ioc容器 四：生命周期 五：多种注册方式 一：什么是IOC容器 IOC容器是Inversion Of Control的缩写，翻译的意思就是控制反转。 …...
ARM工控机/网关- 钡铼技术
一、NXP处理器ARM控制器的介绍 NXP半导体是汽车、穿戴、消费电子等领域中智能机器解决方案的领先供应商。其产品线庞大，包括处理器、微控制器、快速设计平台、ARM控制器等。在物联网控制、汽车电子、安全应用等领域，NXP处理器ARM控制器已成为半导体行业的…...
docker详细操作--未完待续
docker介绍 docker官网: Docker：加速容器应用程序开发 harbor官网：Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台，用于将应用程序及其依赖项（如库、运行时环…...
大数据学习（132）-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏： 👑哲学语录: 用力所能及，改变世界。 💖如果觉得博主的文章还不错的话，请点赞👍收藏⭐️留言Ǵ…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达，从日常对话到特定领域的文档（例如医学文档）（Heritage 2013；Landmark、Gulbrandsen 和 Svenevei…...
在Mathematica中实现Newton-Raphson迭代的收敛时间算法（一般三次多项式）
考察一般的三次多项式，以r为参数： p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]； 此多项式的根为： 尽管看起来这个多项式是特殊的，其实一般的三次多项式都是可以通过线性变换化为这个形式…...
论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON，依赖模型推理阶段输出进行差分测试，但在训练阶段是不可行的，因为训练阶段直到最后才有固定输出，中间过程是不断变化的。API 库覆盖低，因为各个 API 都是在各种具体场景下使用。…...
uniapp 集成腾讯云 IM 富媒体消息（地理位置/文件）
UniApp 集成腾讯云 IM 富媒体消息全攻略（地理位置/文件） 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型，核心实现方式： 标准消息类型：直接使用 SDK 内置类型（文件、图片等）自…...
stm32wle5 lpuart DMA数据不接收
配置波特率9600时，需要使用外部低速晶振...
无需布线的革命：电力载波技术赋能楼宇自控系统-亚川科技
无需布线的革命：电力载波技术赋能楼宇自控系统 在楼宇自动化领域，传统控制系统依赖复杂的专用通信线路，不仅施工成本高昂，后期维护和扩展也极为不便。电力载波技术（PLC）的突破性应用，彻底改变了…...
篇章一 论坛系统——前置知识
目录 1.软件开发 1.1 软件的生命周期 1.2 面向对象 1.3 CS、BS架构 1.CS架构编辑 2.BS架构 1.4 软件需求 1.需求分类 2.需求获取 1.5 需求分析 1. 工作内容 1.6 面向对象分析 1.OOA的任务 2.统一建模语言UML 3. 用例模型 3.1 用例图的元素 3.2 建立用例模型 …...
【Pandas】pandas DataFrame dropna
Pandas2.2 DataFrame Missing data handling 方法描述DataFrame.fillna([value, method, axis, …])用于填充 DataFrame 中的缺失值（NaN）DataFrame.backfill(*[, axis, inplace, …])用于**使用后向填充（即“下一个有效观测值”）…...