C语言数据类型
C 数据类型
在 C 语言中,数据类型指的是用于声明不同类型的变量或函数的一个广泛的系统。变量的类型决定了变量存储占用的空间,以及如何解释存储的位模式。
C 中的类型可分为以下几种:
1 基本类型:
它们是算术类型,包括两种类型:整数类型和浮点类型。
2 枚举类型:
它们也是算术类型,被用来定义在程序中只能赋予其一定的离散整数值的变量。
3 void 类型:
类型说明符 void 表明没有可用的值。
4 派生类型:
它们包括:指针类型、数组类型、结构类型、共用体类型和函数类型。
数组类型和结构类型统称为聚合类型。函数的类型指的是函数返回值的类型。
整数类型
下表列出了关于标准整数类型的存储大小和值范围的细节:
类型 存储大小 值范围
char 1 字节 -128 到 127 或 0 到 255
unsigned char 1 字节 0 到 255
signed char 1 字节 -128 到 127
int 2 或 4 字节 -32,768 到 32,767 或 -2,147,483,648 到 2,147,483,647
unsigned int 2 或 4 字节 0 到 65,535 或 0 到 4,294,967,295
short 2 字节 -32,768 到 32,767
unsigned short 2 字节 0 到 65,535
long 4 字节 -2,147,483,648 到 2,147,483,647
unsigned long 4 字节 0 到 4,294,967,295
注意,各种类型的存储大小与系统位数有关,但目前通用的以64位系统为主。
为了得到某个类型或某个变量在特定平台上的准确大小,您可以使用 sizeof 运算符。表达式 sizeof(type) 得到对象或类型的存储字节大小。下面的实例演示了获取 int 类型的大小:
实例
#include <stdio.h>
#include <limits.h>int main()
{printf("int 存储大小 : %lu \n", sizeof(int));return 0;
}
%lu 为 32 位无符号整数,详细说明查看 C 库函数 - printf()。
浮点类型
下表列出了关于标准浮点类型的存储大小、值范围和精度的细节:
类型 存储大小 值范围 精度
float 4 字节 1.2E-38 到 3.4E+38 6 位有效位
double 8 字节 2.3E-308 到 1.7E+308 15 位有效位
long double 16 字节 3.4E-4932 到 1.1E+4932 19 位有效位
头文件 float.h 定义了宏,在程序中可以使用这些值和其他有关实数二进制表示的细节。下面的实例将输出浮点类型占用的存储空间以及它的范围值:
实例
#include <stdio.h>
#include <float.h>int main()
{printf("float 存储最大字节数 : %lu \n", sizeof(float));printf("float 最小值: %E\n", FLT_MIN );printf("float 最大值: %E\n", FLT_MAX );printf("精度值: %d\n", FLT_DIG );return 0;
}
%E 为以指数形式输出单、双精度实数,详细说明查看 C 库函数 - printf()。
编译并执行上面的程序时,它会产生下列结果:
float 存储最大字节数 : 4
float 最小值: 1.175494E-38
float 最大值: 3.402823E+38
精度值: 6
void 类型
void 类型指定没有可用的值。它通常用于以下三种情况下:
序号 类型与描述
1 函数返回为空
C 中有各种函数都不返回值,或者您可以说它们返回空。不返回值的函数的返回类型为空。例如 void exit (int status);
2 函数参数为空
C 中有各种函数不接受任何参数。不带参数的函数可以接受一个 void。例如 int rand(void);
3 指针指向 void
类型为 void * 的指针代表对象的地址,而不是类型。例如,内存分配函数 void *malloc( size_t size ); 返回指向 void 的指针,可以转换为任何数据类型。
相关文章:

C语言数据类型
C 数据类型 在 C 语言中,数据类型指的是用于声明不同类型的变量或函数的一个广泛的系统。变量的类型决定了变量存储占用的空间,以及如何解释存储的位模式。 C 中的类型可分为以下几种: 1 基本类型: 它们是算术类型,…...
)
华为OD机试真题Python实现【水仙花数】真题+解题思路+代码(20222023)
水仙花数 题目 所谓的水仙花数是指一个n位的正整数其各位数字的n次方的和等于该数本身, 例如153 = 1^3 + 5^3 + 3^3,153是一个三位数 🔥🔥🔥🔥🔥👉👉👉👉👉👉 华为OD机试(Python)真题目录汇总 输入 第一行输入一个整数N, 表示 N 位的正整数 N 在3…...

【华为OD机试模拟题】用 C++ 实现 - 非严格递增连续数字序列(2023.Q1)
最近更新的博客 华为OD机试 - 入栈出栈(C++) | 附带编码思路 【2023】 华为OD机试 - 箱子之形摆放(C++) | 附带编码思路 【2023】 华为OD机试 - 简易内存池 2(C++) | 附带编码思路 【2023】 华为OD机试 - 第 N 个排列(C++) | 附带编码思路 【2023】 华为OD机试 - 考古…...

RN面试题
RN面试题1.React Native相对于原生的ios和Android有哪些优势?1.性能媲美原生APP 2.使用JavaScript编码,只要学习这一种语言 3.绝大部分代码安卓和IOS都能共用 4.组件式开发,代码重用性很高 5.跟编写网页一般,修改代码后即可自动刷…...
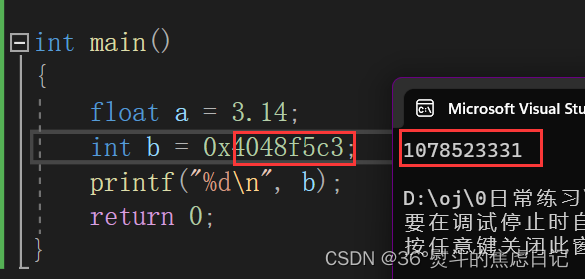
【数据存储】浮点型在内存中的存储
目录 一、存储现象 二、IEEE标准规范 1.存储 2.读取 三、举例验证 1.存储 2.读取 浮点型存储的标准是IEEE(电气电子工程师学会)754制定的。 一、存储现象 浮点数由于其有小数点的特殊性,有很多浮点数是不能精确存储的,如&#…...
:异常处理)
Servlet笔记(8):异常处理
1、错误页面配置 web.xml <!-- servlet 定义 --> <servlet><servlet-name>ErrorHandler</servlet-name><servlet-class>ErrorHandler</servlet-class> </servlet> <!-- servlet 映射 --> <servlet-mapping><servle…...

stm32f407探索者开发板(二十一)——窗口看门狗
文章目录一、窗口看门狗概述1.1 看门狗框图1.2 窗口看门狗工作过程总结1.3 超时时间1.4 为什么需要窗口看门狗1.5 其他注意事项二、常用寄存器和库函数2.1 控制寄存器WWDG_ CR2.2 配置寄存器WWDG_ CFR2.3 状态寄存器WWDG_SR三、手写窗口看门狗3.1 配置过程3.2 初始化窗口看门狗…...
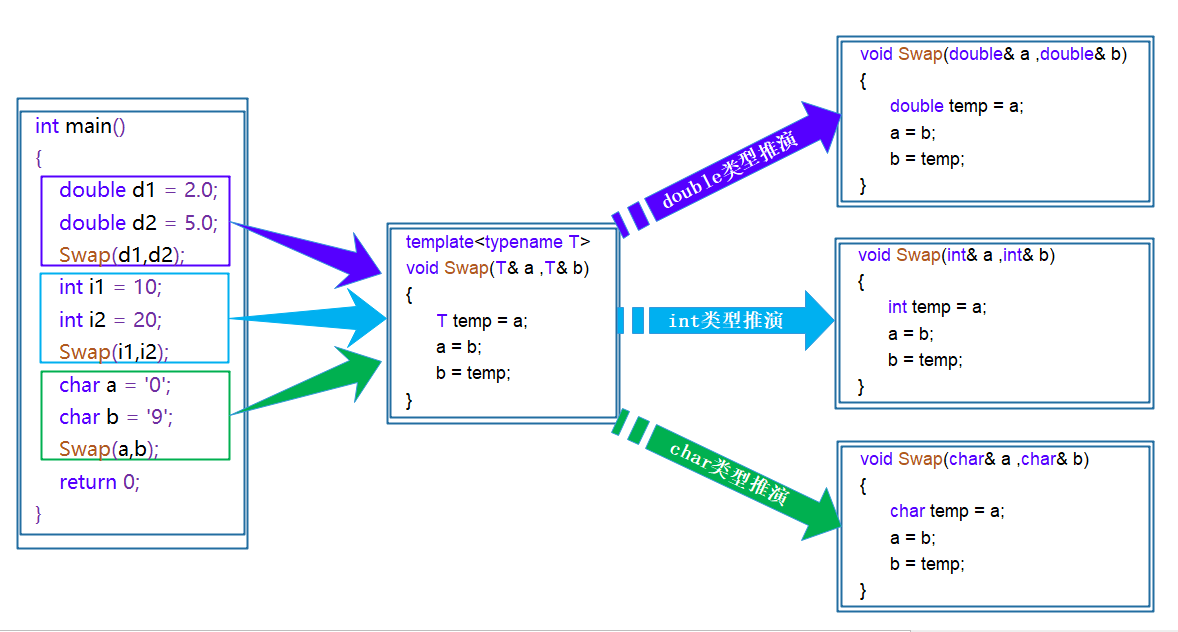
C++ 模板
1. 泛型编程实现一个通用的交换函数,使用函数重载虽然可以实现,但是有以 下几个不好的地方:1. 重载的函数仅仅是类型不同,代码复用率比较低,只要有新类型出现时,就需要用户自己增加对应的函数2. 代码的可维…...

C++中的友元及运算符重载
友元 意义 程序中,有些私有属性也想让类外特殊的一些函数或者类进行访问,就要用到友元技术 关键字 friend 友元的三种实现 全局函数做友元 class Room{friend void test(Person &p);//friend class test;public:string phone_number;private:string…...
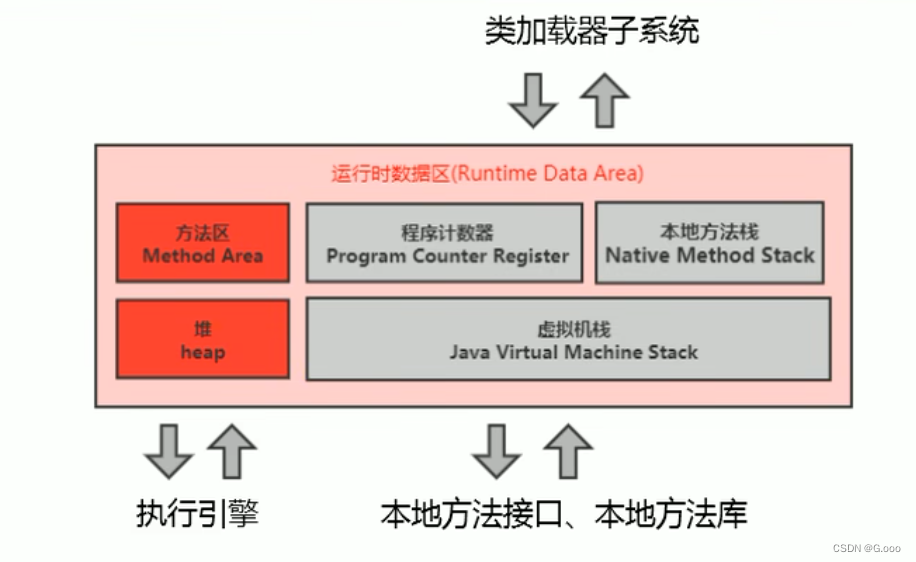
五、运行时数据区内部结构、JVM中的线程
内存是非常重要的系统资源,是硬盘和cpu的中间仓库及桥梁,承载着操作系统和应用程序的实时运行。JVM内存布局规定了Java在运行过程种内存申请、分配‘、管理的策略,保证了JVM的高效稳定运行,不同的JVM对于内存的划分方式和管理机制…...
Codeforces Round #848 (Div. 2)A-C
传送门 目录 A. Flip Flop Sum 代码: B. The Forbidden Permutation 代码: C. Flexible String 代码: A. Flip Flop Sum 题意:给你一个长度为n的数组(数组元素只为1或者-1),你要且只能进行…...
机器学习笔记之近似推断(一)从深度学习角度认识推断
机器学习笔记之近似推断——从深度学习角度认识推断引言推断——基本介绍精确推断难的原因虽然能够表示,但计算代价太大无法直接表示引言 本节是一篇关于推断总结的博客,侧重点在于深度学习模型中的推断任务。 推断——基本介绍 推断(Inference\text{…...
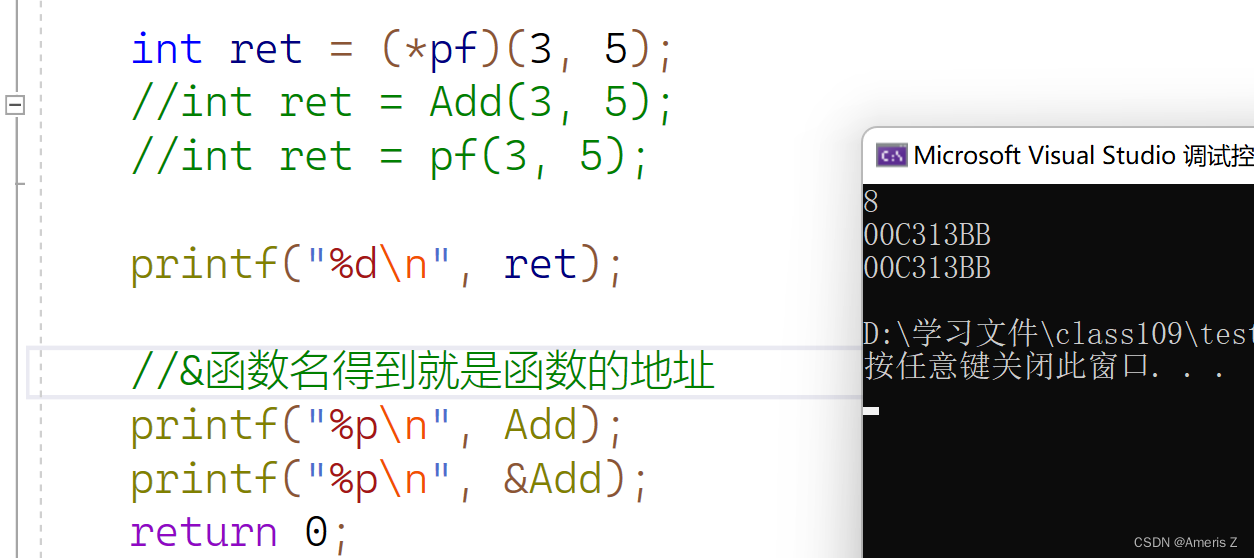
指针的进阶
一、字符指针 int main() {char ch w;char* pc &ch;//pc就是字符指针//const char *p "abcdef";//这里其实是把字符串"abcdef"的首地址放入了指针p中//*p w;//这是错误的无法修改值(可以看到这里绿色波浪线警告)char arr[] …...

一元二次方程方程的类
1 问题设计一个一元二次方程的类,其中包括能够反映一元二次方程的属性与操作行为,然后再设计一个测试类,检测类的使用情况。2 方法使用package语句将方程的属性即计算跟的方法封装在一个有包名的类中,包名为tom.jiafei,…...

Ask林曦|来回答,30个你关心的日常问题(二)
在林曦老师的线上书法直播课上,上课前后的聊天时间里,时常有同学向林曦老师提问,这些问题涵盖了日常生活的诸多方面,从身体的保养,到快乐的法门,皆是大家感兴趣的,也都共同关切的。 暄桐教室…...

哪款电容笔适合开学季?电容笔和Apple Pencil的区别
其实,市场上一般的电容笔和Apple Pencil的最大差别,就在于Apple Pencil与普通电容笔两者的重量和压感。然而,由于苹果电容笔价格过高,目前电容笔的市场份额逐渐转向平替电容笔,平替电容笔其性能也逐渐得到改善。下面&a…...

Qt之Qprocess
QProcess 可用于完成启动外部程序,并与之交互通信。 一、启动外部程序的两种方式 1)一体式:void QProcess::start(const QString & program,const QStringList &arguments,OpenMode mode ReadWrite) 外部程序启动后&…...

为什么不愿意专升本 学历有什么用
专升本包括两种形式普通专升本和成人专升本。普通专升本毕业是全日制学历,考试仅有一次,错过不能补考所以考生不愿意选择,成人专升本毕业是非全日制学历,学历被国家承认,和普通高校毕业证有相同的使用效力。为何考生不…...

构造函数的使用大全
概述 在C中创建一个对象时,通常需要做一些数据初始化的工作,因此便提供了一个特殊的成员函数 —— 构造函数。一般情况下,并不需要程序员主动调用构造函数,而是在创建对象时,由系统自动调用。构造函数可以由程序员定义…...
ASP.NET Core MVC 项目 IOC容器
目录 一:什么是IOC容器 二:简单理解内置Ioc容器 三:依赖注入内置Ioc容器 四:生命周期 五:多种注册方式 一:什么是IOC容器 IOC容器是Inversion Of Control的缩写,翻译的意思就是控制反转。 …...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...
