温故知新:dfs模板-843. n-皇后问题
n−n−皇后问题是指将 nn 个皇后放在 n×nn×n 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。
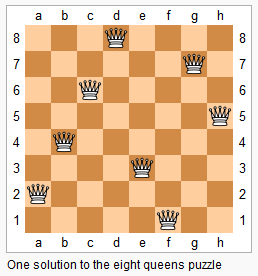
现在给定整数 nn,请你输出所有的满足条件的棋子摆法。
输入格式
共一行,包含整数 nn。
输出格式
每个解决方案占 nn 行,每行输出一个长度为 nn 的字符串,用来表示完整的棋盘状态。
其中 . 表示某一个位置的方格状态为空,Q 表示某一个位置的方格上摆着皇后。
每个方案输出完成后,输出一个空行。
注意:行末不能有多余空格。
输出方案的顺序任意,只要不重复且没有遗漏即可。
数据范围
1≤n≤91≤n≤9
输入样例:
4
输出样例:
.Q..
...Q
Q...
..Q...Q.
Q...
...Q
.Q..
思路
深度优先搜索,我们需要排除永远不可能的情况(剪枝),首先是初始化二维数组,把二维数组初始化为'.'
for(int i=0;i<n;i++){for(int j=0;j<n;j++){g[i][j]='.';}}深度优先搜索分两步走,第一步是判断有没有走到终点,走到终点就输出我们需要的答案
if(u==n){for(int i=0;i<n;i++) puts(g[i]);puts("");return;}第二步是遍历每一行,利用条件判断,找到可以符合条件的情况(该题是行,对角线,反对角线不能被使用过),然后改变使用状态,修改字符数组的内容,递归调用dfs函数,恢复现场,把状态和字符数组的内容都修改回来
int x=u;for(int y=0;y<n;y++){if(!col[y]&&!dg[y+x]&&!udg[y-x+n]){col[y]=dg[y+x]=udg[y-x+n]=true;g[x][y]='Q';dfs(x+1);col[y]=dg[y+x]=udg[y-x+n]=false;g[x][y]='.';}}这里把u和i更换成了x和y,感觉更加方便理解
代码
#include<bits/stdc++.h>
using namespace std;int n;
const int N=20;
char g[N][N];
bool col[N],dg[N],udg[N];void dfs(int u)
{if(u==n){for(int i=0;i<n;i++) puts(g[i]);puts("");return;}int x=u;for(int y=0;y<n;y++){if(!col[y]&&!dg[y+x]&&!udg[y-x+n]){col[y]=dg[y+x]=udg[y-x+n]=true;g[x][y]='Q';dfs(x+1);col[y]=dg[y+x]=udg[y-x+n]=false;g[x][y]='.';}}
}int main()
{scanf("%d",&n);for(int i=0;i<n;i++){for(int j=0;j<n;j++){g[i][j]='.';}}dfs(0);return 0;
}
相关文章:

温故知新:dfs模板-843. n-皇后问题
n−n−皇后问题是指将 nn 个皇后放在 nnnn 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。 现在给定整数 nn,请你输出所有的满足条件的棋子摆法。 输入格式 共一行,包含整数 n…...

刷题笔记28——一直分不清的Kruskal、Prim、Dijkstra算法
图算法刷到这块,感觉像是走了一段黑路快回到家一样,看到这三个一直分不太清总是记混的名字,我满脑子想起的是大学数据结构课我坐在第一排,看着我班导一脸无奈,心想该怎么把这个知识点灌进木头脑袋里边呢。有很多算法我…...

Mysql时间同步设置
Mysql时间同步设置 当涉及到设置MySQL数据库时间与电脑同步时,实际的步骤可能会因操作系统和数据库版本的不同而有所差异。以下是一个基本的步骤示例,供您参考: 检查电脑时间: 首先确保电脑操作系统的时间是正确的。 设置MySQL时…...
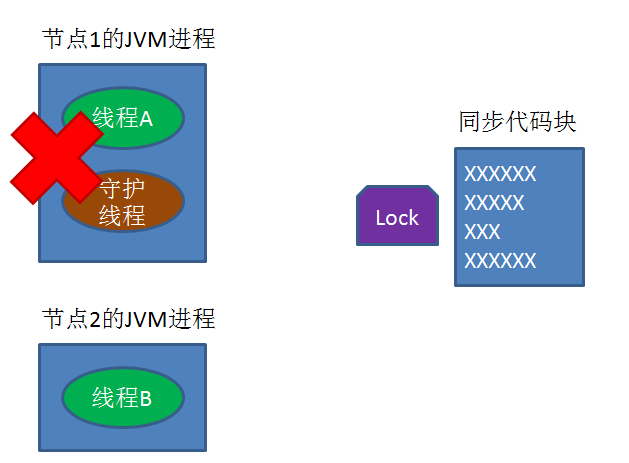
如何理解分布式锁?
分布式锁的实现有哪些? 1.Memcached分布式锁 利用Memcached的add命令。此命令是原子操作,只有在key不存在的情况下,才能add成功,也就意味着线程得到了锁。 2.Reids分布式锁 和Memcached的方式类似,利用Redis的setn…...
windows 远程连接 ubuntu桌面xrdp
更新 sudo apt update安装组件 sudo apt-get install xorg sudo apt-get install xserver-xorg-core sudo apt-get install xorgxrdp sudo apt install xfce4 xfce4-goodies xorg dbus-x11 x11-xserver-utilsxrdp sudo apt install xrdp sudo systemctl status xrdp sudo …...

数据采集时使用HTTP代理IP效率不高怎么办?
在进行数据采集时,使用HTTP代理 可以帮助我们实现隐私保护和规避封禁的目的。然而,有时候我们可能会遇到使用HTTP代理 效率不高的问题,如连接延迟、速度慢等。本文将为您分享解决这一问题的实用技巧,帮助您提高数据采集效率&#…...
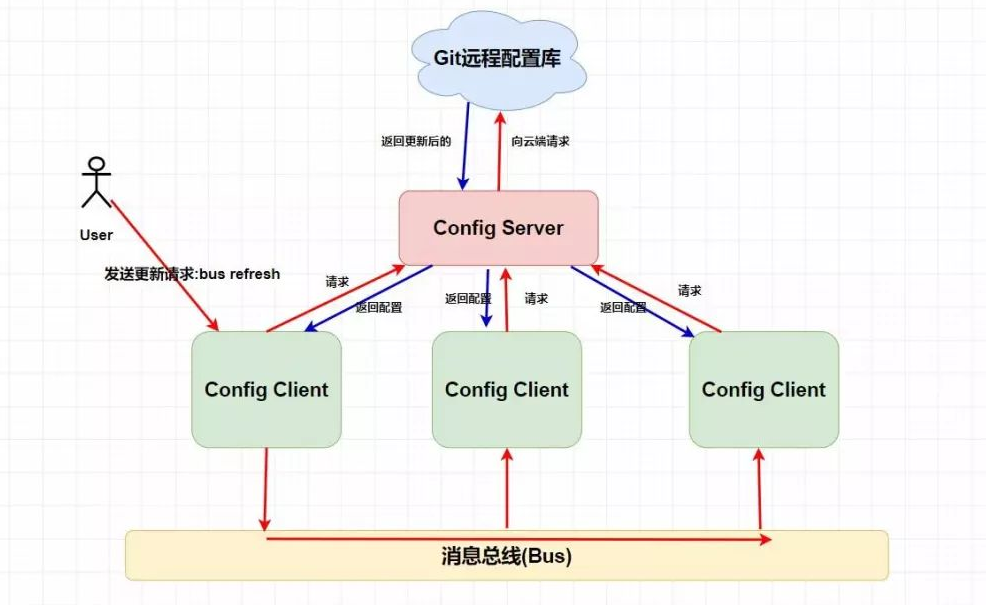
你了解的SpringCloud核心组件有哪些?他们各有什么作用?
SpringCloud 1.什么是 Spring cloud Spring Cloud 为最常见的分布式系统模式提供了一种简单且易于接受的编程模型,帮助开发人员构建有弹性的、可靠的、协调的应用程序。Spring Cloud 构建于 Spring Boot 之上,使得开发者很容易入手并快速应用于生产中。…...

【Gradle-10】不可忽视的构建分析
1、前言 构建性能对于生产力至关重要。 随着项目越来越复杂,花费在构建上的时间就越长,开发效率就越低。 通过分析构建过程,可以了解项目构建的时间都花在哪,以及项目存在哪些潜在的问题,找到构建瓶颈,解…...

2034. 股票价格波动
给你一支股票价格的数据流。数据流中每一条记录包含一个 时间戳 和该时间点股票对应的 价格 。 不巧的是,由于股票市场内在的波动性,股票价格记录可能不是按时间顺序到来的。某些情况下,有的记录可能是错的。如果两个有相同时间戳的记录出现…...

JavaScript 事件详解细节
JavaScript 事件详解细节 JavaScript 中的事件是前端开发中非常重要的一个概念。通过事件,我们可以捕捉和响应用户与网页的交互,比如点击按钮、输入文字等。这篇博客文章将详细介绍 JavaScript 中的事件,希望能帮助你更好地理解和使用这一功…...
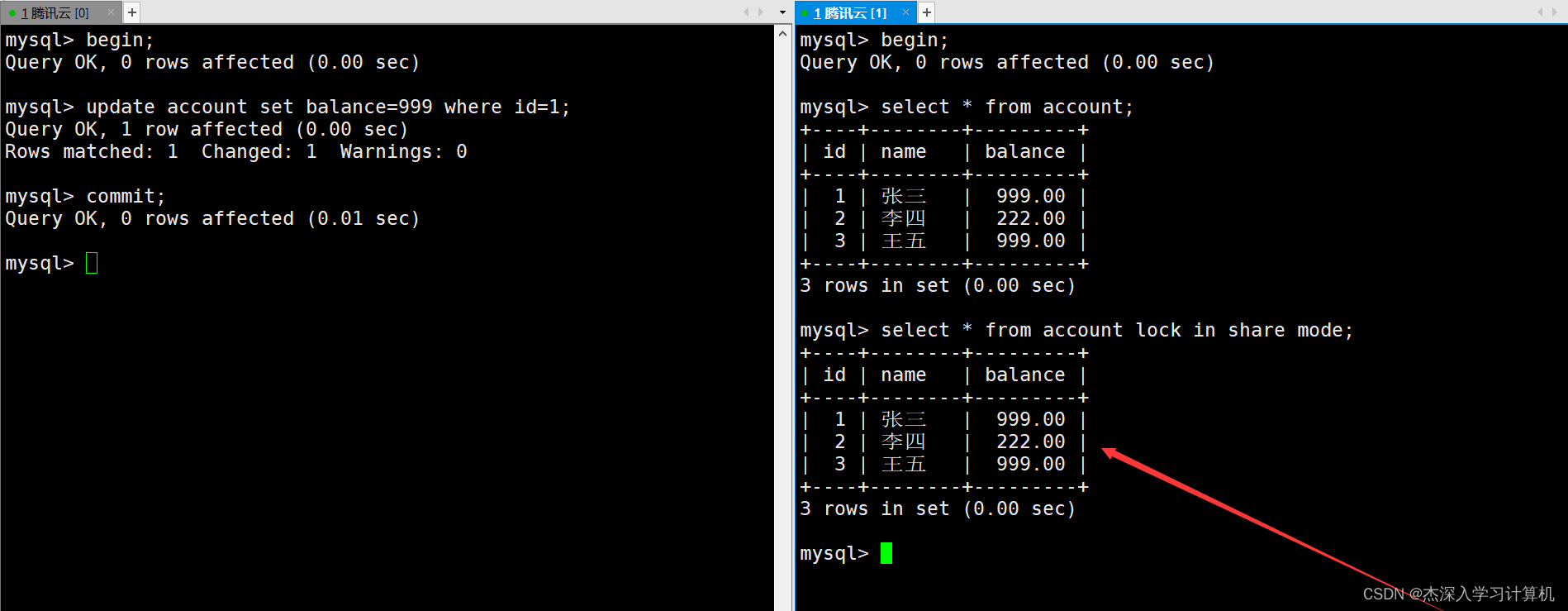
【MySQL】事务管理
目录 MySQL事务管理 事务的概念 事务的版本支持 事务的提交方式 事务的相关演示 事务的隔离级别 查看与设置隔离级别 读未提交(Read Uncommitted) 读提交(Read Committed) 可重复读(Repeatable Read…...

Git 学习笔记 | Git 基本操作命令
Git 学习笔记 | Git 基本操作命令 Git 学习笔记 | Git 基本操作命令文件的四种状态查看文件状态忽略文件 Git 学习笔记 | Git 基本操作命令 文件的四种状态 版本控制就是对文件的版本控制,要对文件进行修改、提交等操作,首先要知道文件当前在什么状态&…...
)
第五章:最新版零基础学习 PYTHON 教程—Python 字符串操作指南(第七节 - Python 中的字符串模板类)
在字符串模块中,模板类允许我们为输出规范创建简化的语法。该格式使用由 $ 和有效 Python 标识符(字母数字字符和下划线)组成的占位符名称。用大括号将占位符括起来,使其后面可以跟更多的字母数字字母,且中间不留空格。写入 $$ 会创建一个转义的 $。 Python 字符串模板:…...
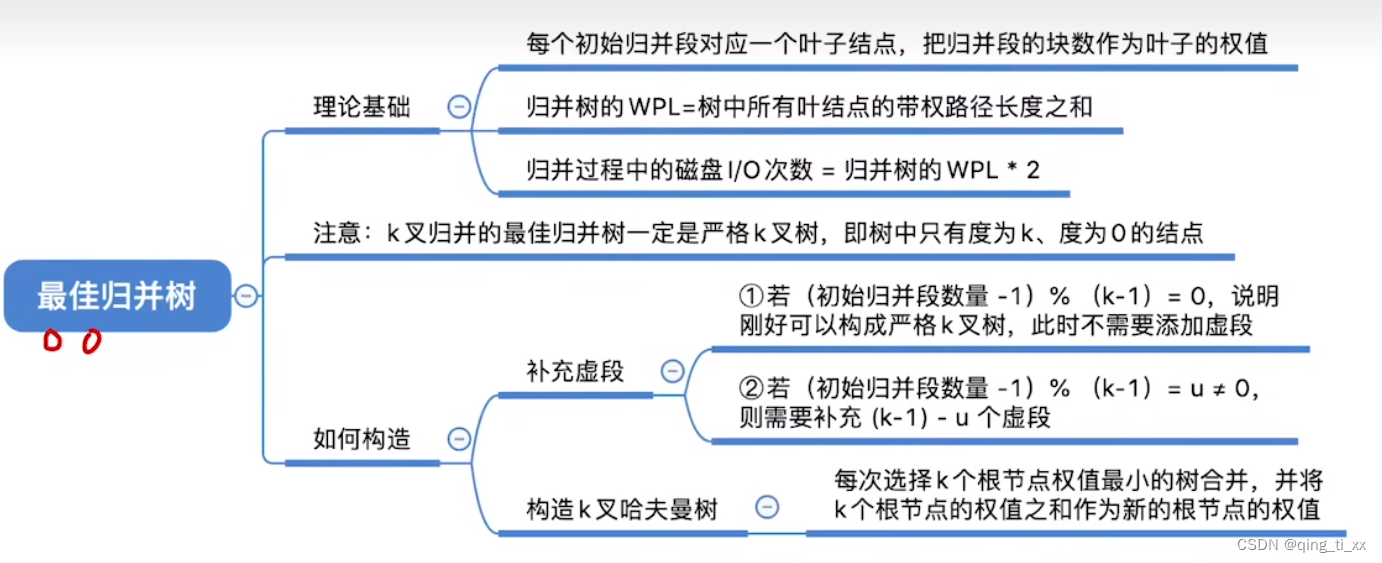
第八章 排序 十四、最佳归并树
目录 一、定义 二、多路最佳归并树 三、多路最佳归并树少了一个归并段 四、总结 一、定义 最佳归并树是指将若干个有序序列合并成一个有序序列的一种方式,使得所有合并操作的总代价最小的一棵二叉树。其中,代价通常指合并两个有序序列的操作次数或比…...

Python 中,类的方法的标准注释模板
在 Python 中,类的标准注释通常遵循以下格式: class 类名:"""类的简要描述属性:- 属性1 (类型): 属性1的描述- 属性2 (类型): 属性2的描述方法:- 方法1(): 方法1的描述- 方法2(): 方法2的描述示例:>>> 对象 类名()>>>…...
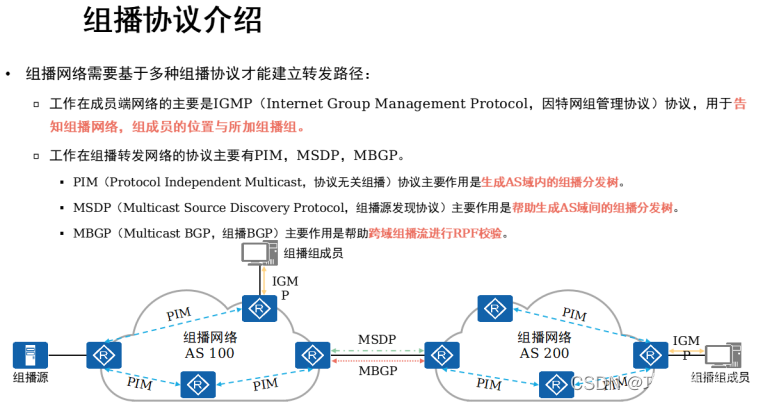
IPSG技术和IP组播
1,IPSG技术概述 实验: DHCP snooping IPSG 拓扑: 需求: 1,实现PC1 和PC2 动态获取IP地址 2, 在SW2 配置DHCP snooping 实现DHCP 服务器的安全 3, 在 连接PC 1 和 PC2 的 接口上 做IPSG ,防止终端…...

【大数据】Apache NiFi 助力数据处理及分发
Apache NiFi 助力数据处理及分发 1.什么是 NiFi ?2.NiFi 的核心概念3.NiFi 的架构4.NiFi 的性能预期和特点5.NiFi 关键特性的高级概览 1.什么是 NiFi ? 简单的说,NiFi 就是为了解决不同系统间数据自动流通问题而建立的。虽然 dataflow 这个术…...

什么是 SRE?一文详解 SRE 运维体系
目录 可观测性系统 故障响应 故障复盘 测试与发布 容量规划 自动化工具开发 用户体验 可观测性系统 在任何有一定规模的企业内部,一旦推行起来整个SRE的运维模式,那么对于可观测性系统的建设将变得尤为重要,而在整个可观测性系统中&a…...
【Docker】初识 Docker,Docker 基本命令的使用,Dockerfile 自定义镜像的创建
文章目录 前言:项目部署的挑战一、初识 Docker1.1 什么是 Docker1.2 Docker 与 虚拟机的区别1.3 镜像和容器以及镜像托管平台1.4 Docker的架构解析1.5 Docker 在 CentOS 中的安装 二、Docker 的基本操作2.1 操作 Docker 镜像命令2.1.1 镜像操作相关命令2.1.2 示例一…...

【Docker】简易版harbor部署
文章目录 依赖于docker-compose下载添加执行权限测试 安装harbor下载解压修改配置文件部署配置开机自启动登录验证 使用harbor登录打标签上传下载 常见问题 依赖于docker-compose 下载 curl -L “https://github.com/docker/compose/releases/download/2.22.0/docker-compose-…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...
