【重拾C语言】六、批量数据组织(二)线性表——分类与检索(主元排序、冒泡排序、插入排序、顺序检索、对半检索)
目录
前言
六、批量数据组织——数组
6.1~3 数组基础知识
6.4 线性表——分类与检索
6.4.1 主元排序
6.4.2 冒泡排序
6.4.3 插入排序
6.4.4 顺序检索(线性搜索)
6.4.5 对半检索(二分查找)
算法比较
前言
线性表是一种常见的数据结构,用于存储一组具有相同类型的元素。本文主要介绍了下面几种常见的线性表的排序和检索算法:
-
主元排序(主元选择排序):这是一种选择排序算法,它通过选择主元(通常是最小或最大元素)并将其放置在正确的位置来进行排序。该算法重复选择主元并移动它,直到所有元素都有序排列。
-
冒泡排序:这是一种简单的排序算法,它通过多次比较和交换相邻元素的方式将较大的元素逐渐向右移动。通过重复这个过程直到所有元素都有序排列,最终实现排序。
-
插入排序:这是一种通过将元素逐个插入已排序序列的合适位置来完成排序的算法。在插入排序过程中,将当前元素与已排序序列中的元素逐个比较,直到找到合适的插入位置。
-
顺序检索:也称为线性搜索,是一种简单直接的搜索方法,从线性表的起始位置开始逐个比较元素,直到找到目标元素或遍历完整个线性表。
-
对半检索(二分查找):对于已排序的线性表,可以使用对半检索来提高搜索效率。该算法通过将目标元素与线性表的中间元素进行比较,然后根据比较结果将搜索范围缩小一半。重复这个过程,直到找到目标元素或确定目标元素不存在。
六、批量数据组织——数组
6.1~3 数组基础知识
【重拾C语言】六、批量数据组织(一)数组(数组类型、声明与操作、多维数组;典例:杨辉三角、矩阵乘积、消去法)-CSDN博客![]() https://blog.csdn.net/m0_63834988/article/details/133580645?spm=1001.2014.3001.5502
https://blog.csdn.net/m0_63834988/article/details/133580645?spm=1001.2014.3001.5502
6.4 线性表——分类与检索
6.4.1 主元排序
主元排序(主元选择排序)是一种简单的排序算法,它通过选择线性表中的主元(也称为枢轴元素)并将其放置在正确的位置上来实现排序。主元排序算法的基本思想是:选择一个主元,将线性表中小于主元的元素放在主元的左边,将大于主元的元素放在主元的右边,然后对主元的左右两部分递归地进行排序,直到整个线性表有序。
void mainElementSort(int arr[], int left, int right) {if (left < right) {int pivot = partition(arr, left, right); // 获取主元的位置mainElementSort(arr, left, pivot - 1); // 对主元左边的元素进行排序mainElementSort(arr, pivot + 1, right); // 对主元右边的元素进行排序}
}int partition(int arr[], int left, int right) {int pivotIndex = left; // 将第一个元素作为主元int pivotValue = arr[left];int i, j;for (i = left + 1; i <= right; i++) {if (arr[i] < pivotValue) {pivotIndex++;swap(arr, i, pivotIndex); // 将小于主元的元素交换到主元的左边}}swap(arr, left, pivotIndex); // 将主元放置在正确的位置上return pivotIndex;
}void swap(int arr[], int i, int j) {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;
}在主元排序算法中,首先选择一个主元,这里选择线性表的第一个元素作为主元。然后,从主元的下一个位置开始遍历线性表,将小于主元的元素逐个交换到主元的左边,并记录交换次数。最后,将主元放置在正确的位置上,即交换次数加一的位置。这样,主元左边的元素都小于主元,主元右边的元素都大于主元。
接下来,对主元的左右两部分分别递归地应用主元排序算法,直到每个子序列只有一个元素为止。最终,整个线性表就会被排序。
主元排序是一种简单但有效的排序算法,其平均时间复杂度为O(nlogn),其中n是线性表的长度。然而,如果每次选择的主元都不合理,可能导致算法的性能下降。因此,在实际应用中,选择合适的主元策略对算法的性能至关重要。
6.4.2 冒泡排序
冒泡排序(Bubble Sort)是一种简单的排序算法,它通过反复交换相邻的元素将最大的元素逐步 "冒泡" 到数组的末尾,从而实现排序。冒泡排序算法的基本思想是:比较相邻的两个元素,如果它们的顺序不正确,则交换它们,直到整个数组有序。
void bubbleSort(int arr[], int n) {int i, j;for (i = 0; i < n - 1; i++) { // 通过n-1次循环将最大元素冒泡到末尾for (j = 0; j < n - 1 - i; j++) { // 每次循环比较相邻的两个元素if (arr[j] > arr[j + 1]) {int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp; // 交换位置,使更大的元素向后移动}}}
}在冒泡排序算法中,外层循环控制冒泡的轮数,内层循环用于比较相邻的两个元素并进行交换。每一轮循环都将最大的元素冒泡到当前未排序部分的末尾。通过n-1次循环,就可以将整个数组排序完成。
冒泡排序的时间复杂度为O(n^2),其中n是数组的长度。尽管冒泡排序的时间复杂度较高,但它的实现较为简单,且在某些情况下可能具有一定的优势。然而,在处理大型数据集时,通常会选择更高效的排序算法。
6.4.3 插入排序
插入排序(Insertion Sort)是一种简单直观的排序算法,它通过构建有序序列,不断将未排序的元素插入到已排序序列中的适当位置,从而实现排序。插入排序算法的基本思想是:将数组分为已排序和未排序两部分,每次从未排序部分取出一个元素,将其插入到已排序部分的正确位置。
void insertionSort(int arr[], int n) {int i, j, key;for (i = 1; i < n; i++) {key = arr[i]; // 从未排序部分取出一个元素j = i - 1;while (j >= 0 && arr[j] > key) {arr[j + 1] = arr[j]; // 将比key大的元素向后移动j--;}arr[j + 1] = key; // 将key插入到正确的位置上}
}在插入排序算法中,将数组分为已排序部分(初始为空)和未排序部分。从未排序部分依次取出元素,将其与已排序部分的元素从右向左进行比较,直到找到合适的位置插入。为了插入元素,需要将比插入元素大的元素向右移动一个位置,为插入元素留出空间。最后,将插入元素放置在正确的位置上,即完成一次插入操作。
通过n-1次循环,就可以将整个数组排序完成。
插入排序的时间复杂度为O(n^2),其中n是数组的长度。尽管插入排序的时间复杂度较高,但它对小型数据集的排序效果较好,并且在部分已经有序的情况下,插入排序的性能会更加出色。
6.4.4 顺序检索(线性搜索)
顺序检索(Sequential Search),也称为线性搜索,是一种简单直观的搜索算法。顺序检索算法的基本思想是:从给定的数据集合中按顺序逐个比较元素,直到找到目标元素或搜索完整个数据集合。
int sequentialSearch(int arr[], int n, int target) {for (int i = 0; i < n; i++) {if (arr[i] == target) {return i; // 找到目标元素,返回元素的索引}}return -1; // 未找到目标元素,返回-1表示失败
}顺序检索算法通过遍历数据集合,逐个比较元素和目标元素是否相等。如果找到了目标元素,就返回该元素在数据集合中的索引;如果遍历完整个数据集合仍未找到目标元素,则返回-1表示搜索失败。
顺序检索的时间复杂度为O(n),其中n是数据集合的大小。由于顺序检索需要逐个比较元素,它的效率较低,特别是在大型数据集合上。然而,在小型数据集合或无序数据集合中进行简单搜索时,顺序检索是一种常用的方法。
6.4.5 对半检索(二分查找)
对半检索(Binary Search),也称为二分查找,是一种高效的搜索算法,用于在有序数组或列表中查找目标元素。对半检索算法的基本思想是:将数组或列表分成两部分,通过比较目标元素与中间元素的大小关系,确定目标元素可能在的那一部分,然后继续在该部分中进行查找,缩小搜索范围,直到找到目标元素或确定目标元素不存在。
int binarySearch(int arr[], int n, int target) {int low = 0;int high = n - 1;while (low <= high) {int mid = (low + high) / 2; // 计算中间元素的索引if (arr[mid] == target) {return mid; // 找到目标元素,返回元素的索引} else if (arr[mid] < target) {low = mid + 1; // 目标元素在右半部分,调整搜索范围} else {high = mid - 1; // 目标元素在左半部分,调整搜索范围}}return -1; // 未找到目标元素,返回-1表示失败
}对半检索算法通过比较目标元素与中间元素的大小关系,将数组或列表分成两部分。如果中间元素等于目标元素,就返回中间元素的索引;如果中间元素小于目标元素,说明目标元素在右半部分,将搜索范围缩小到右半部分;如果中间元素大于目标元素,说明目标元素在左半部分,将搜索范围缩小到左半部分。通过不断缩小搜索范围,最终可以找到目标元素或确定目标元素不存在。
对半检索的前提是数组或列表必须是有序的,因为它利用了有序性质进行二分查找。对半检索的时间复杂度为O(log n),其中n是数组或列表的长度。由于每次都将搜索范围缩小一半,对半检索的效率非常高。
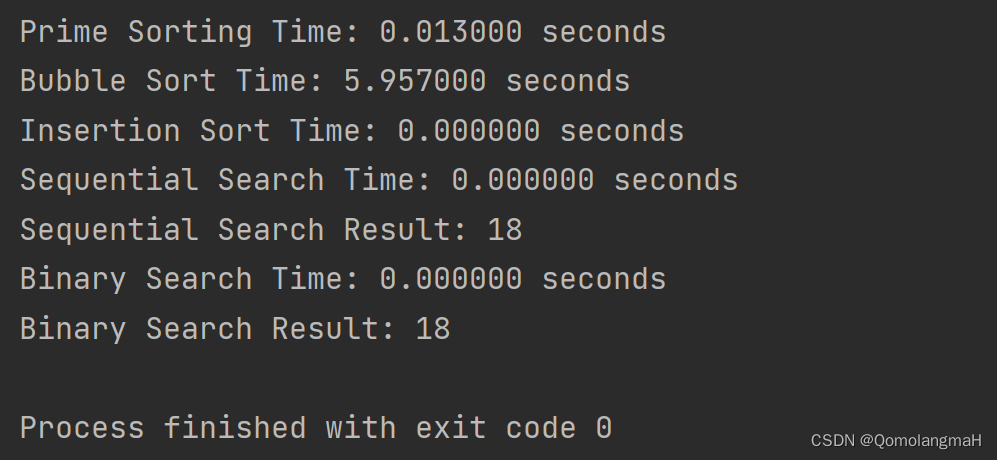
算法比较
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define SIZE 100000
void swap(int arr[], int i, int j) {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;
}
int partition(int arr[], int left, int right) {int pivotIndex = left; // 将第一个元素作为主元int pivotValue = arr[left];int i, j;for (i = left + 1; i <= right; i++) {if (arr[i] < pivotValue) {pivotIndex++;swap(arr, i, pivotIndex); // 将小于主元的元素交换到主元的左边}}swap(arr, left, pivotIndex); // 将主元放置在正确的位置上return pivotIndex;
}void primeSort(int arr[], int left, int right) {if (left < right) {int pivot = partition(arr, left, right); // 获取主元的位置primeSort(arr, left, pivot - 1); // 对主元左边的元素进行排序primeSort(arr, pivot + 1, right); // 对主元右边的元素进行排序}
}void bubbleSort(int arr[], int n) {int i, j;for (i = 0; i < n - 1; i++) { // 通过n-1次循环将最大元素冒泡到末尾for (j = 0; j < n - 1 - i; j++) { // 每次循环比较相邻的两个元素if (arr[j] > arr[j + 1]) {int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp; // 交换位置,使更大的元素向后移动}}}
}void insertionSort(int arr[], int n) {int i, j, key;for (i = 1; i < n; i++) {key = arr[i]; // 从未排序部分取出一个元素j = i - 1;while (j >= 0 && arr[j] > key) {arr[j + 1] = arr[j]; // 将比key大的元素向后移动j--;}arr[j + 1] = key; // 将key插入到正确的位置上}
}int sequentialSearch(int arr[], int n, int target) {for (int i = 0; i < n; i++) {if (arr[i] == target) {return i; // 找到目标元素,返回元素的索引}}return -1; // 未找到目标元素,返回-1表示失败
}int binarySearch(int arr[], int n, int target) {int low = 0;int high = n - 1;while (low <= high) {int mid = (low + high) / 2; // 计算中间元素的索引if (arr[mid] == target) {return mid; // 找到目标元素,返回元素的索引} else if (arr[mid] < target) {low = mid + 1; // 目标元素在右半部分,调整搜索范围} else {high = mid - 1; // 目标元素在左半部分,调整搜索范围}}return -1; // 未找到目标元素,返回-1表示失败
}double measureTime(clock_t start, clock_t end) {return ((double) (end - start)) / CLOCKS_PER_SEC;
}int main() {int arr[SIZE];// 使用时间作为随机数种子srand(time(NULL));// 待排序的数组for (int i = 0; i < SIZE; i++) {arr[i] = rand();};int n = sizeof(arr) / sizeof(arr[0]); // 数组的长度int target = 7; // 待搜索的目标元素// 测量主元排序算法的运行时间clock_t start = clock();primeSort(arr, 0, n);clock_t end = clock();printf("Prime Sorting Time: %.6f seconds\n", measureTime(start, end));// 测量冒泡排序算法的运行时间start = clock();bubbleSort(arr, n);end = clock();printf("Bubble Sort Time: %.6f seconds\n", measureTime(start, end));// 测量插入排序算法的运行时间start = clock();insertionSort(arr, n);end = clock();printf("Insertion Sort Time: %.6f seconds\n", measureTime(start, end));// 测量顺序检索算法的运行时间start = clock();int sequentialSearchResult = sequentialSearch(arr, n, target);end = clock();printf("Sequential Search Time: %.6f seconds\n", measureTime(start, end));printf("Sequential Search Result: %d\n", sequentialSearchResult);// 测量对半检索算法的运行时间start = clock();int binarySearchResult = binarySearch(arr, n, target);end = clock();printf("Binary Search Time: %.6f seconds\n", measureTime(start, end));printf("Binary Search Result: %d\n", binarySearchResult);return 0;
}
相关文章:

【重拾C语言】六、批量数据组织(二)线性表——分类与检索(主元排序、冒泡排序、插入排序、顺序检索、对半检索)
目录 前言 六、批量数据组织——数组 6.1~3 数组基础知识 6.4 线性表——分类与检索 6.4.1 主元排序 6.4.2 冒泡排序 6.4.3 插入排序 6.4.4 顺序检索(线性搜索) 6.4.5 对半检索(二分查找) 算法比较 前言 线性表是一种常…...

24 Python的sqlite3模块
概述 在上一节,我们介绍了Python的shutil模块,包括:shutil模块中一些常用的函数。在这一节,我们将介绍Python的sqlite3模块。sqlite3模块是Python中的内置模块,用于与SQLite数据库交互。SQLite是一个轻量级的磁盘数据库…...

ARM-流水灯
.text .global _start _start: 1、设置GPIOE寄存器的时钟使能 RCC_MP_AHB$ENSETR[4]->1 0x50000a28LDR R0,0X50000A28 LDR R1,[R0] 从R0起始地址的4字节数据取出放在R1 ORR R1,R1,#(0X3<<4) 第4位设置为1 STR R1,[R0] 写回2、设置PE10、PE8、PF10管脚为输出模式 …...

【虚拟机】NAT 模式下访问外网
目录 一、NAT 模式的作用原理 二、配置 NAT 模式实现外网访问 1、配置NAT模式的网段 2、虚拟机选择 VMnet8 网卡 3、IP地址设为自动分配 一、NAT 模式的作用原理 NAT模式下,虚拟机的系统会把宿主机当作一个大路由器,发送的网络请求和数据都是先发给…...
React 入门笔记
前言 国庆值班把假期拆了个稀碎, 正好不用去看人潮人海, 趁机会赶个晚集入门一下都火这么久的 React 前端技术. 话说其实 n 年前也了解过一丢丢来着, 当时看到一上来就用 JS 写 DOM 的套路直接就给吓退了, 扭头还去看 Vue 了🤣, 现在从市场份额 社区活度来看, 确实…...
Ubuntu MySQL
在安装前,首先看你之前是否安装过,如果安装过,但是没成功,就要先卸载。 一、卸载 1.查看安装 dpkg --list | grep mysql 有东西,就说明您之前安装过mysql。 2.卸载 先停掉server sudo systemctl stop mysql.servic…...

大数据软件系统开发框架
大数据处理框架是用于处理大规模数据集的软件工具和平台,它们可以帮助分析、存储和处理庞大的数据量。以下是一些常见的大数据处理框架,希望对大家有所帮助。北京木奇移动技术有限公司,专业的软件外包开发公司,欢迎交流合作。 1.A…...

rust变量
一 、变量定义 (一)语法格式 使用let关键字定义变量 let varname: type value; 如,let a: i32 78;也可以不显式指定类型 let varname value; 如,let a 78;一些例子 1.布尔 let t true; let f: bool false;2.整数 let a …...

蓝桥杯---第一讲 递归与递推
文章目录 前言Ⅰ. 递归实现指数型枚举0x00 算法思路0x00 代码书写0x00 思考总结 Ⅱ. 递归实现排列型枚举0x00 算法思路0x01代码书写0x02 思考总结 Ⅲ. 简单斐波那契0x00 算法思路0x01 代码书写 Ⅳ. 费解的开关0x00 算法思路0x01 代码书写 Ⅴ. 递归实现组合型枚举0x00 算法思路0…...
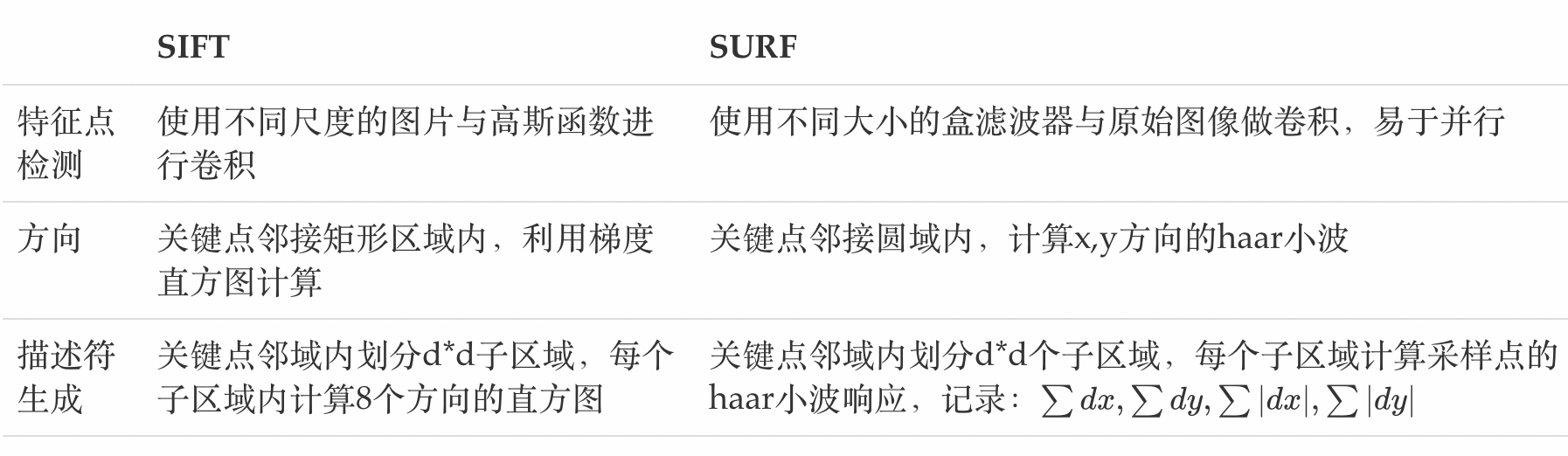
OpenCV 15(SIFT/SURF算法)
一、SIFT Harris和Shi-Tomasi角点检测算法,这两种算法具有旋转不变性,但不具有尺度不变性,以下图为例,在左侧小图中可以检测到角点,但是图像被放大后,在使用同样的窗口,就检测不到角点了。 尺度…...
)
前端二维码图片解析图片识别/网络图片解析成链接/图片网络链接转本地链接(Js/Vue/Jquery)
注:需要用到canvas/jsqr/jquery! 1、远程图片链接本地化 页面: <!-- 识别二维码用的 canvas--> <canvas class"canvas" ref"canvas" style"display: none"></canvas> 1.创建图片 get2: fu…...
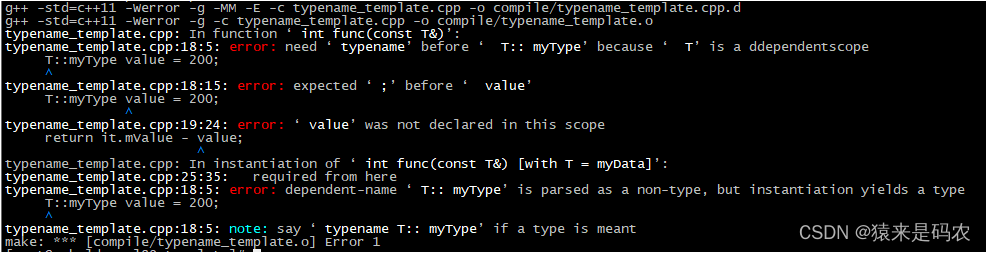
模板中的依赖类型使用 --- typename
依赖类型,顾名思义就是依赖于模板参数的类型,在使用这种类型时,必须使用 typename,否则编译器是无法知道是在使用类型,还是类的成员(因为类的静态成员的使用方法也是T::xxx,这跟某个类中的类型的…...
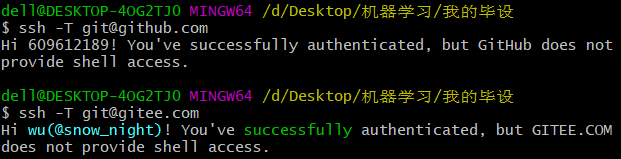
git 同时配置 gitee github
git 同时配置 gitee github 1、 删除C:\Users\dell\.ssh目录。 在任意目录右击——》Git Bash Here,打开Git Bash窗口,下方命令在Git Bash窗口输入。 2、添加git全局范围的用户名和邮箱 git config --global user.email "609612189qq.com" …...

2023.10.8 面试
面试工作1年的程序员 看到生涩才入职场不久的面试者,为人也相对诚恳的模样,我对此是很欣赏的态度。 因为完全看到了自己毕业1年时的场景。 简历上写的事情,讨论起来,描述不清楚,为此感到遗憾,因我本人也会…...

【前端】js实现队列功能 先进后出 先进先出 等
也可以定义一个定时器 不断的去取队列 执行任务 用一个flag定义队列正在执行中, 如果没有执行 则定时器不断的去调用队列,(因为会随时添加一个任务到队列中) 队列任务结束后 自动取下一个队列 也可以边加队列 边取 队列定义 function Queue() {//初始化队列(使用…...

07.数据持久化之文件操作
1. 文件操作 计算机的文件,就是存储在某种 长期储存设备 上的一段 数据 长期存储设备包括:硬盘、U 盘、移动硬盘、光盘… 文本文件和二进制文件 文本文件 可以使用 文本编辑软件 查看本质上还是二进制文件例如:python 的源程序 二进制文件…...
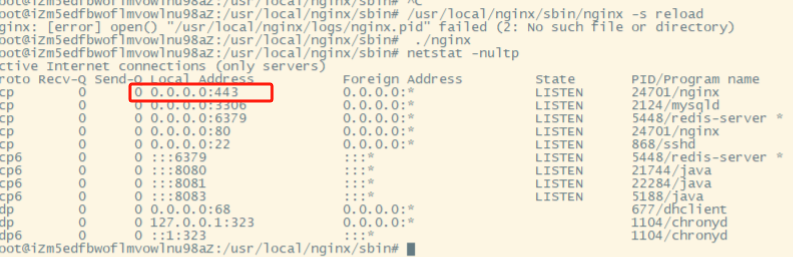
nginx开启https配置之后网页无法访问问题处理
背景说明 最近新购服务器部署nginx之后按照之前的方式部署前端项目并配置https之后访问页面显示:无法访问.新的服务器ECS系统和之前相同,nginx安装方式也相同,nginx配置方式也是相同.但是访问还是显示无法访问.下面简单记录一下问题处理过程. 处理过程 1.https访问之后无法访问…...
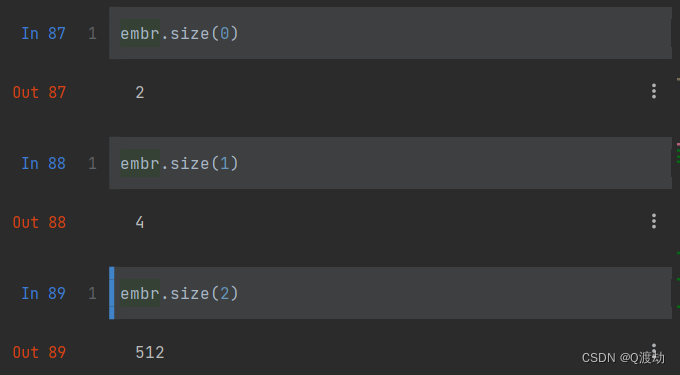
文本嵌入层
目录 1、文本嵌入层的作用 2、代码演示 3、构建Embeddings类来实现文本嵌入层 1、文本嵌入层的作用 无论是源文本嵌入层还是目标文本嵌入,都是为了将文本词汇中的数字表示转变为向量表示,希望在这样的高维空间中捕捉词汇之间的关系 2、代码演示 Emb…...
如何搭建自动化测试框架
关于测试框架的好处,比如快速回归提高测试效率,提高测试覆盖率等这里就不讨论了。这里主要讨论自动化框架包含哪些内容,以及如何去设计一个测试框架。 1. 什么是自动化测试框架? 它是由一个或多个自动化测试基础模块、自动化测试…...
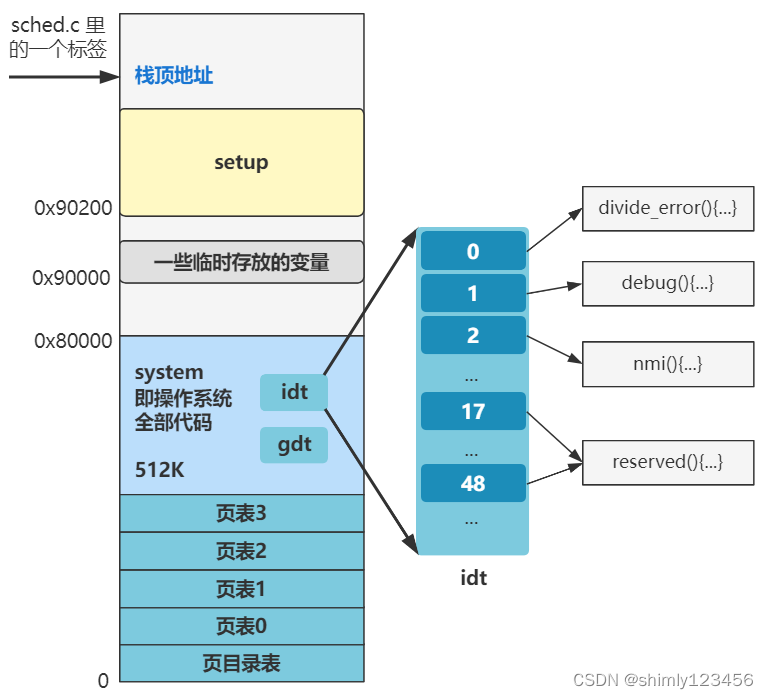
抄写Linux源码(Day17:你的键盘是什么时候生效的?)
回忆我们需要做的事情: 为了支持 shell 程序的执行,我们需要提供: 1.缺页中断(不理解为什么要这个东西,只是闪客说需要,后边再说) 2.硬盘驱动、文件系统 (shell程序一开始是存放在磁盘里的,所以需要这两个东…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...
