python--排序总结
1.快速排序
a.原理
快速排序的基本思想是在待排序的 n 个元素中任取一个元素(通常取第一个元素)作为基准,把该元素放人最终位置后,整个数据序列被基准分割成两个子序列,所有小于基准的元素放置在前子序列中,所有大于基准的元素放置在后子序列中,并把基准排在这两个子序列的中间,这个过程称为划分。然后对两个子序列分别重复上述过程,直到每个子序列内只有一个元素或空为止。
这是一种二分法思想,每次将整个无序序列一分为二。归位一个元素,对两个子序列采用同样的方式进行排序,直到子序列的长度为1或0为止。(摘自算法分析与设计第二版 有删改)
b.代码
def quick_sort(arr):if len(arr) <= 1:return arrpivot = arr[len(arr) // 2]#轴left = [x for x in arr if x < pivot]middle = [x for x in arr if x == pivot]right = [x for x in arr if x > pivot]return quick_sort(left) + middle + quick_sort(right)
s = list(map(float,input("输入用空格分隔的数字:").split()))#
print(quick_sort(s)) 
2.插入排序
a.原理
插入排序,一般也被称为直接插入排序。对于少量元素的排序,它是一个有效的算法。插入排序是一种最简单的排序方法,它的基本思想是将一个记录插入到已经排好序的有序表中,从而一个新的、记录数增1的有序表。在其实现过程使用双层循环,外层循环对除了第一个元素之外的所有元素,内层循环对当前元素前面有序表进行待插入位置查找,并进行移动。
b.代码
def insert_sort(arr):for i in range(1, len(arr)):key = arr[i]j = i - 1while j >= 0 and arr[j] > key:arr[j + 1] = arr[j]j -= 1arr[j + 1] = keyreturn arrarr = [3, 5, 2, 4, 1]
print(insert_sort(arr))
3.冒泡排序
a.原理
重复地走访过要排序的元素列,依次比较两个相邻的元素,如果顺序错误就把他们交换过来。走访元素的工作是重复地进行,直到没有相邻元素需要交换,也就是说该元素列已经排序完成
b.代码
def bubble_sort(arr):for i in range(len(arr)):for j in range(len(arr) - i - 1):if arr[j] > arr[j + 1]:arr[j], arr[j + 1] = arr[j + 1], arr[j]return arrarr = [3, 5, 2, 4, 1]
print(bubble_sort(arr))
4.希尔排序
a.原理
希尔排序是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。
希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至 1 时,整个文件恰被分成一组,算法便终止。
b.代码
def shell_sort(arr):n = len(arr)gap = n // 2while gap > 0:for i in range(gap, n):temp = arr[i]j = iwhile j >= gap and arr[j - gap] > temp:arr[j] = arr[j - gap]j -= gaparr[j] = tempgap //= 2return arrarr = [3, 5, 2, 4, 1]
print(shell_sort(arr))
5.选择排序
a.原理
选择排序是一种简单直观的排序算法。它的工作原理是:第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾。以此类推,直到全部待排序的数据元素的个数为零。选择排序是不稳定的排序方法
b.代码
def selection_sort(arr):for i in range(len(arr)):min_index = ifor j in range(i + 1, len(arr)):if arr[min_index] > arr[j]:min_index = jarr[i], arr[min_index] = arr[min_index], arr[i]return arrarr = [3, 5, 2, 4, 1]
print(selection_sort(arr))
6.堆排序
a.原理
堆排序是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
发明人:罗伯特·弗洛伊德
b.代码
def heap_sort(arr):n = len(arr)# 建立大顶堆for i in range(n // 2 - 1, -1, -1):heapify(arr, n, i)# 将堆顶元素与末尾元素交换,并重新调整大顶堆for i in range(n - 1, 0, -1):arr[i], arr[0] = arr[0], arr[i]heapify(arr, i, 0)return arrdef heapify(arr, n, i):largest = il = 2 * i + 1r = 2 * i + 2if l < n and arr[largest] < arr[l]:largest = lif r < n and arr[largest] < arr[r]:largest = rif largest != i:arr[i], arr[largest] = arr[largest], arr[i]heapify(arr, n, largest)arr = [3, 5, 2, 4, 1]
print(heap_sort(arr))
7.归并排序
a.原理
归并排序的基本思想是首先将 a [0.. n 一1]看成 n 个长度为1的有序表,将相邻的 k ( k ≥2)个有序子表成对归并,得到 n / k 个长度为 k 的有序子表:然后再将这些有序子表继续归并,得到 n /k2个长度为 k 的有序子表,如此反复进行下去,最后得到一个长度为 n 的有序表。由于整个排序结果放在一个数组中,所以不需要特别地进行合并操作。若 k =2,即归并是在相邻的两个有序子表中进行的,称为二路归并排序。若 k >2,即归并操作在相邻的多个有序子表中进行,则叫多路归并排序。(摘自算法分析与设计第二版)
b.代码
def merge_sort(arr):if len(arr) > 1:mid = len(arr) // 2left = arr[:mid]right = arr[mid:]merge_sort(left)merge_sort(right)i = j = k = 0while i < len(left) and j < len(right):if left[i] < right[j]:arr[k] = left[i]i += 1else:arr[k] = right[j]j += 1k += 1while i < len(left):arr[k] = left[i]i += 1k += 1while j < len(right):arr[k] = right[j]j+= 1k += 1arr = [12, 11, 13, 5, 6, 7]
merge_sort(arr)
print(arr)
有待补充。
相关文章:

python--排序总结
1.快速排序 a.原理 快速排序的基本思想是在待排序的 n 个元素中任取一个元素(通常取第一个元素)作为基准,把该元素放人最终位置后,整个数据序列被基准分割成两个子序列,所有小于基准的元素放置在前子序列中࿰…...

进化的隐藏水印:深度学习提升版权保护的鲁棒性
一、前言 过去几年,以网络视频为代表的泛网络视听领域的崛起,是互联网经济飞速发展最为夺目的大事件之一。泛网络视听领域不仅是21世纪以来互联网领域的重要基础应用、大众文化生活的主要载体,而且在推动中国经济新旧动能转化方面也发挥了重…...
Jenkins配置项目教程
在上一篇[Jenkins的使用教程](https://blog.csdn.net/weixin_43787492/article/details/129028131?spm1001.2014.3001.5501)中我介绍了如何创建一个项目 Jenkins在创建项目中提供了很多功能供我们选择,这里我将对配置项目做一个较完整的介绍Jenkins配置项目0、所有…...

C++多继承,虚继承部分总结与示例
tags: C OOP 写在前面 写一下多继承, 虚继承的一些部分, 包括一些例子. 多继承 简介 多继承是指从多个直接基类中产生派生类的能力. 多继承的派生类继承了所有父类的属性, 所以会带来一些复杂的问题. 示例1: 多继承用法与调用顺序 #include <string> #include <…...
程序员35岁以后就没有出路了吗?听听京东10年测开的分析
国内的互联网行业发展较快,所以造成了技术研发类员工工作强度比较大,同时技术的快速更新又需要员工不断的学习新的技术。因此淘汰率也比较高,超过35岁的基层研发类员工,往往因为家庭原因、身体原因,比较难以跟得上工作…...
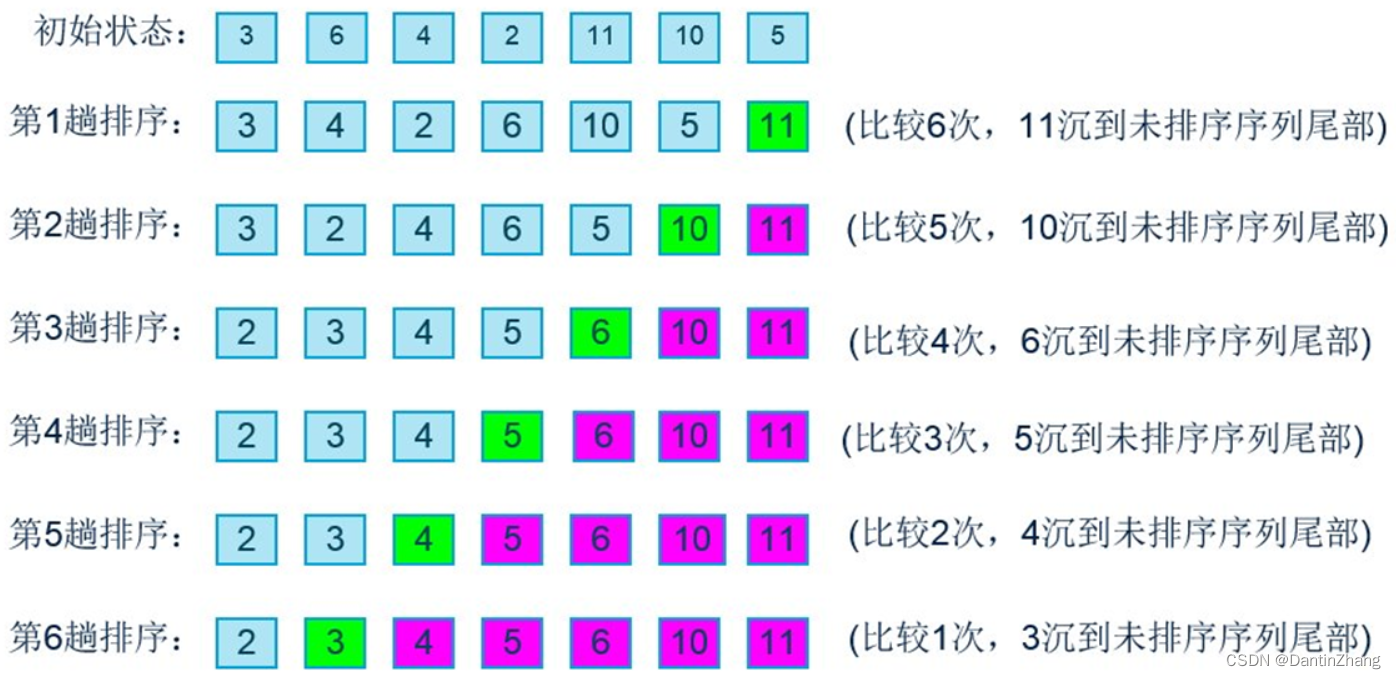
数据结构(六):冒泡排序、选择排序、插入排序、希尔排序、快速排序
数据结构(六)一、大O表示法二、冒泡排序三、选择排序一、大O表示法 在计算机中采用粗略的度量来描述计算机算法的效率,这种方法被称为“大O”表示法。 我们判断一个算法的效率,不能只凭着算法运行的速度,因为随着数据…...
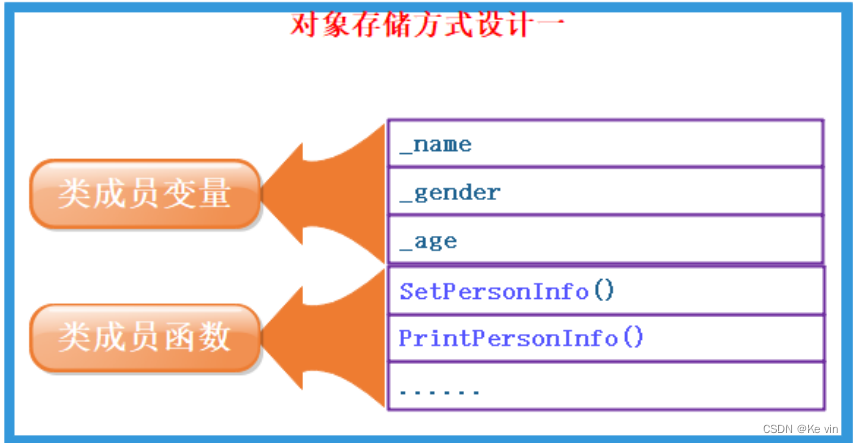
C++之类与对象(上)
目录 一、类的定义 二.类的访问限定及封装 1.访问限定 2.封装 三.类的作用域和实例化 2.类的实例化 四.类的对象大小的计算 1.类成员存储方式 2.结构体内存对齐规则 五.类成员函数的this指针 1.this指针的引出 2.this指针的特性 3.C语言和C实现Stack的对比 一、类的定义 class …...

Java岗面试题--Java并发 计算机网络(日积月累,每日三题)
目录1. 面试题一:在 Java 程序中怎么保证多线程的运行安全?1.1 追问一:Java 线程同步的几种方法?2. 面试题二:JMM3. 面试题三:计算机网络的各层协议及作用?1. 面试题一:在 Java 程序…...
三菱FX3U与威纶MT8071IP走RS422通讯
一、准备工作 1.需要工具: 电脑一台、PLC:三菱FX3U一个、触摸屏:威纶MT8071一个、 (三菱圆形编程口转USB)一根、触摸屏与电脑通讯线一根(T型口数据线)、PLC与触摸屏通讯线:电烙…...

给想考CISP的一点建议
如果你正在考虑参加CISP认证考试,以下是我对你的几点建议: 了解CISP考试: 在报名参加考试之前,要充分了解CISP认证考试的考试内容、考试形式、考试难度等相关信息,这有助于你制定更有效的备考计划。制定备考计划&…...
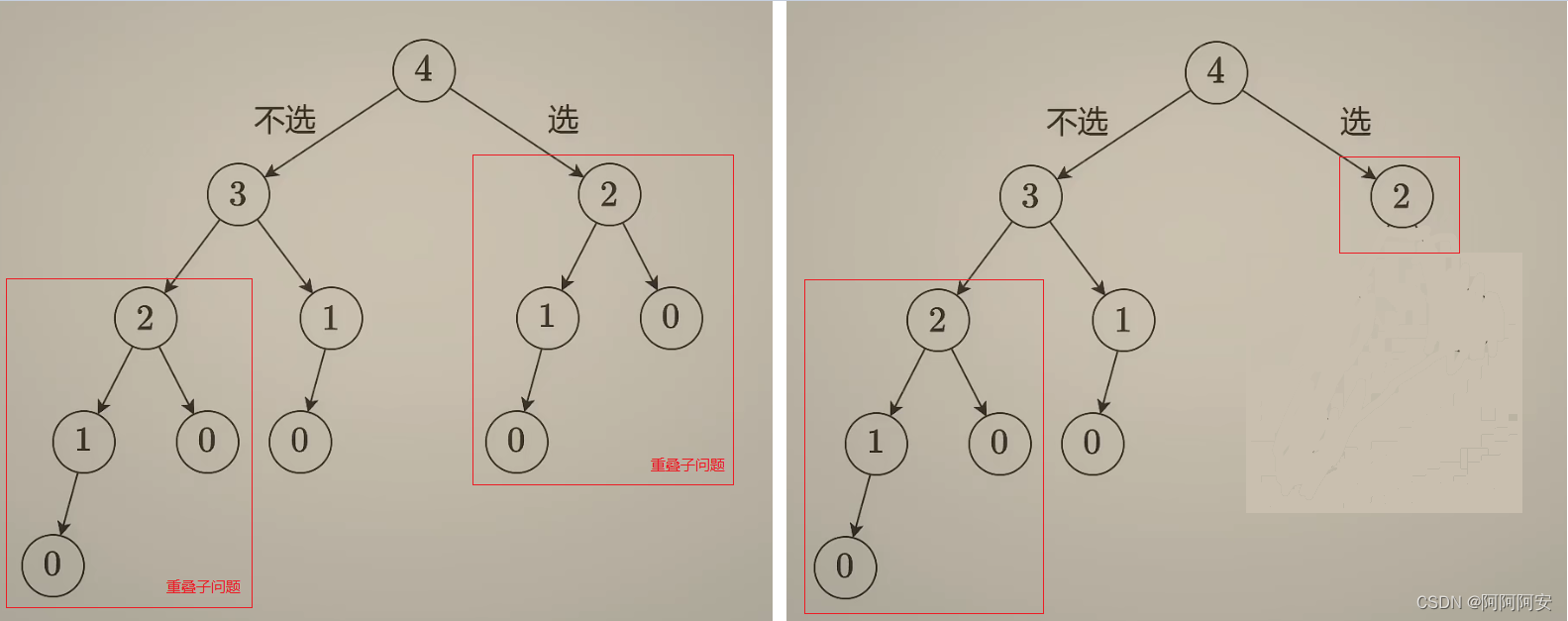
ACM 记忆化搜索
一.记忆化搜索概述 1.概念 搜索是一种简单有效但是效率又很低下的算法结构,其低效的原因主要在于存在很多重叠子问题。而记忆化搜索则是在搜索的基础上,利用数组来记录已经计算出来的重叠子问题状态,进行合理化的剪枝,从而降低时…...

spring框架常用注解简单说明
1、Configuration:标注在类上,相当于把当前类作为spring的xml配置文件中的; 2、Bean:标注在方法上,相当于spring配置文件中的; 3、Service:标注在类上,表明当前类是一个服务层的Be…...

2023-02-24 mysql/innodb-聚合-临时表避免OOM-使用磁盘文件-分析
摘要: mysql/innodb在执行聚合时, 当聚合的数据量太大时, 也就是临时表的大小超过tmp_table_size 限制时, 将进行写磁盘操作, 以避免OOM。 本文记录聚合数据写磁盘的操作。 参考: https://dev.mysql.com/doc/refman/5.7/en/server-system-variables.html#sysvar_tmp_table_…...
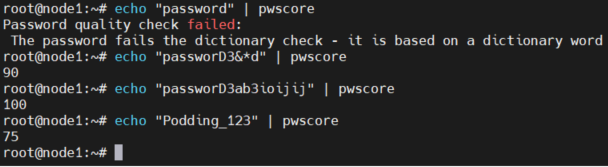
cracklib与libpwquality 评估密码的安全性
一、cracklib 检测密码强弱linux中采用pam pam_cracklib module来实现对密码强度的检测,可以通过配置让linux系统自动检测用户的密码是否为弱密码。yuminstall cracklib # centos apt-get install libcrack2 # ubuntu # 如果需要依赖此库做开发的话需要安装这个 y…...

【Java】保证并发安全的三大特性
一、并发编程三大特性的定义和由来 并发编程这三大特性就是为了在多个线程交替执行任务的过程中保证线程安全性。 二、为什么会出现线程不安全的现象呢? 接下来我们从这三个特性切入来介绍线程不安全的原因。 1.原子性: 一组操作要么全部执行&#…...
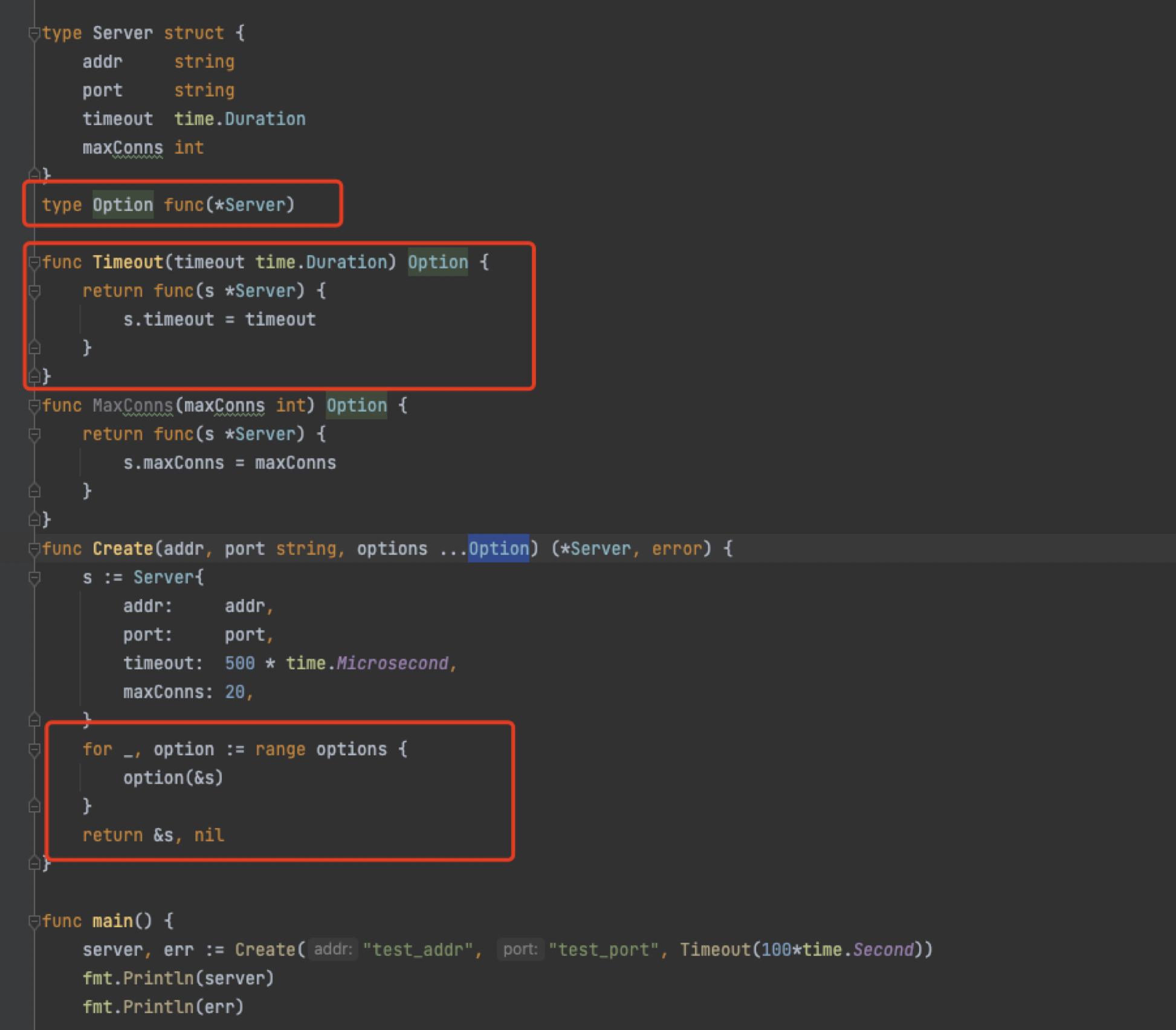
如何优雅的用golang封装配置项(Functional Options)
导读 最近要封装一个公共服务,涉及到配置项的地方总是找不到合理的方案,后来看了一下grpc在配置方面的封装,了解到原来是golang特有的Functional Options编程模式,今天分享给大家,希望你能用到,咱们直接来看…...

Springboot 使用thymeleaf 服务器无法加载resources中的静态资源异常处理
目录一、异常错误二、原因三、解决方法方法1. 将无法编译的静态资源放入可编译目录下方法2. 重新编译项目加载资源方法3. 修改pom.xml资源配置文件方法4. 不连接远程数据库启动,使用本地数据库一、异常错误 Springboot使用thymeleaf,并连接远程数据库启…...

服务端IOS订阅类型支付接入详细说明与注意事项
一、说明 由于本人在开发ios订阅类型支付接入的时候,遇到了很多坑,也查了不少资料,逐步完善了整个ios订阅支付服务端接入的功能,在这里写下总结和一些注意事项的记录,方便未来需要重新接入或者避免一些不必要的坑,这里…...
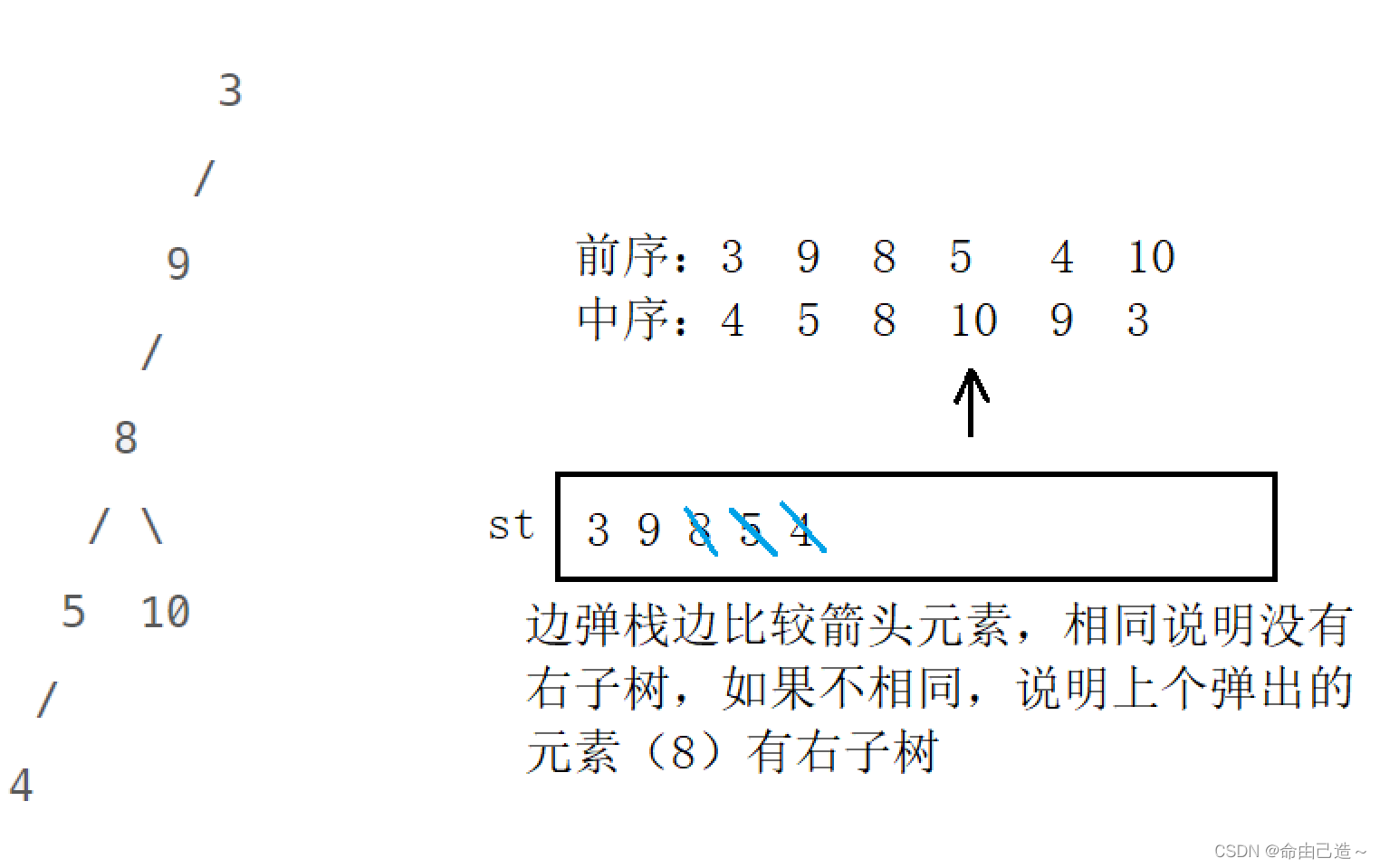
【剑指Offer】重建二叉树(递归+迭代)
重建二叉树一、递归法二、迭代法题目链接 题目描述: 输入某二叉树的前序遍历和中序遍历的结果,请构建该二叉树并返回其根节点。 假设输入的前序遍历和中序遍历的结果中都不含重复的数字。 示例 1: Input: preorder [3,9,20,15,7], inorder [9,3,15,…...

注解@Transactional 原理和常见的坑
这篇文章,会先讲述 Transactional 的 4 种不生效的 Case,然后再通过源码解读,分析 Transactional 的执行原理,以及部分 Case 不生效的真正原因1 项目准备下面是 DB 数据和 DB 操作接口:uidunameusex1张三女2陈恒男3楼仔…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

Linux-进程间的通信
1、IPC: Inter Process Communication(进程间通信): 由于每个进程在操作系统中有独立的地址空间,它们不能像线程那样直接访问彼此的内存,所以必须通过某种方式进行通信。 常见的 IPC 方式包括&#…...

云原生安全实战:API网关Envoy的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关 作为微服务架构的统一入口,负责路由转发、安全控制、流量管理等核心功能。 2. Envoy 由Lyft开源的高性能云原生…...
