【Pytorch笔记】4.梯度计算
深度之眼官方账号 - 01-04-mp4-计算图与动态图机制
前置知识:计算图
可以参考我的笔记:
【学习笔记】计算机视觉与深度学习(2.全连接神经网络)
计算图
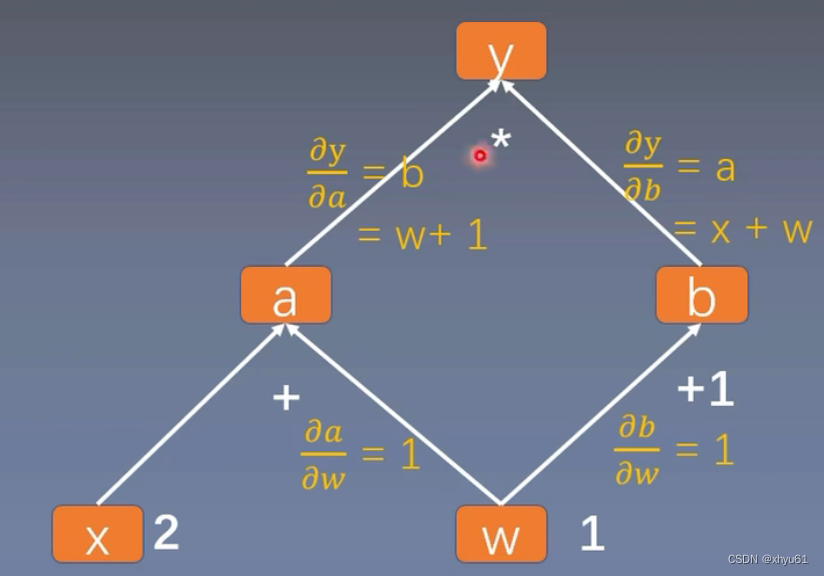
以这棵计算图为例。这个计算图中,叶子节点为x和w。
import torchw = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)a = torch.add(w, x)
b = torch.add(w, 1)
y = torch.mul(a, b)# 调用backward()方法,开始反向求梯度
y.backward()
print(w.grad)print("is_leaf:\n", w.is_leaf, x.is_leaf, a.is_leaf, b.is_leaf, y.is_leaf)
print("gradient:\n", w.grad, x.grad, a.grad, b.grad, y.grad)
输出:
tensor([5.])
is_leaf:True True False False False
gradient:tensor([5.]) tensor([2.]) None None None
由此可见,非叶子节点在最后不会被保留梯度。这是出于节省空间的需要而这样设计的。实际的计算图会非常大,如果每个节点都保留梯度,会占用非常大的存储空间,而这些节点的梯度对于我们学习并没有什么帮助。
如果非要看他们的梯度,可以这样操作:在a = torch.add(w, x)的后面加上一句a.retain_grad(),这样a的梯度就会被存储起来。
输出会变成:
tensor([5.])
is_leaf:True True False False False
gradient:tensor([5.]) tensor([2.]) tensor([2.]) None None
对于节点,还可以看这些节点进行的运算。grad_fn,gradient function的缩写,表示这个节点的tensor是什么运算产生的。加一句:
print("gradient function:\n", w.grad_fn, '\n', x.grad_fn, '\n', a.grad_fn, '\n', b.grad_fn, '\n', y.grad_fn)
会输出
gradient function:NoneNone<AddBackward0 object at 0x000001B1DA3651C0><AddBackward0 object at 0x000001B1DA3651F0><MulBackward0 object at 0x000001B1DA3515B0>
retain_graph
import torchw = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)a = torch.add(w, x)
a.retain_grad()
b = torch.add(w, 1)
y = torch.mul(a, b)# 调用backward()方法,开始反向求梯度
y.backward()
y.backward()
连续两次调用backward()方法,会报这样的错误:
RuntimeError: Trying to backward through the graph a second time (or directly access saved tensors after they have already been freed). Saved intermediate values of the graph are freed when you call .backward() or autograd.grad(). Specify retain_graph=True if you need to backward through the graph a second time or if you need to access saved tensors after calling backward.
原因是我们进行第一次backward()后,计算图就被自动释放掉了,进行第二次backward()时,没有计算图可以计算梯度,于是报错。
解决方案:backward内部添加一个参数:retain_graph=True,意思是计算完梯度后保留计算图。
# 调用backward()方法,开始反向求梯度
y.backward(retain_graph=True)
y.backward()
这样就不会报错了。
gradient
当计算图末部的节点有1个以上时,有时我们会希望他们之间的梯度有一个权重关系。这时就会用上gradient。
import torchw = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)a = torch.add(w, x)
b = torch.add(w, 1)# 不难看出,y0和y1是两个互不干扰的末部节点
y0 = torch.mul(a, b)
y1 = torch.add(a, b)# 将两个末部节点打包起来
loss = torch.cat([y0, y1], dim=0)
grad_tensors = torch.tensor([1., 2.])# 将grad_tensors中的内容作为权重,变成y0+2y1
loss.backward(gradient=grad_tensors)print(w.grad)
输出
tensor([9.])
如果把grad_tensors改成:
grad_tensors = torch.tensor([1., 3.])
输出变成:
tensor([11.])
torch.autograd.grad()
除了加减乘除法,我们还可以对torch进行求导操作。求的是 d ( o u t p u t s ) d ( i n p u t s ) \frac{d(outputs)}{d(inputs)} d(inputs)d(outputs)。
torch.autograd.grad(outputs,inputs,grad_outputs=None,retain_graph=None,create_graph=False)
outputs和inputs已在上述定义中给出;
grad_outputs:多梯度权重;
retain_graph:保留计算图;
create_graph:创建计算图。
import torch# y = x ** 2
x = torch.tensor([3.], requires_grad=True)
y = torch.pow(x, 2)# grad_1 = dy / dx = 2x = 6
grad_1 = torch.autograd.grad(y, x, create_graph=True)
print(grad_1)# grad_2 = d(dy / dx) / dx = 2
grad_2 = torch.autograd.grad(grad_1, x)
print(grad_2)
输出
(tensor([6.], grad_fn=<MulBackward0>),)
(tensor([2.]),)
autograd注意事项
1.梯度不会自动清零
import torchw = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)for i in range(4):a = torch.add(w, x)b = torch.mul(w, x)y = torch.mul(a, b)y.backward()print("w's grad: ", w.grad)# w.grad.zero_()
输出:
w's grad: tensor([8.])
w's grad: tensor([16.])
w's grad: tensor([24.])
w's grad: tensor([32.])
由此可以看出,在不加上注释掉的那一行时,梯度在w处是不断累积的。而如果我们把print后面的那句w.grad.zero_()加上,输出就会变成:
w's grad: tensor([8.])
w's grad: tensor([8.])
w's grad: tensor([8.])
w's grad: tensor([8.])
w.grad.zero_()的意思就是把w处积累的梯度清零。
2.依赖于叶子节点的节点,requires_grad默认为True
可以从上面的代码中发现,我们只有在定义w和x两个tensor时,设置requires_grad为True。这个参数在定义tensor时默认为False。后面我们的a、b、y都没有设置这个参数。
如果我们定义w和x的时候不加上requires_grad=True,那么y.backward()这一步就会报错,因为我们的预设,这两个tensor不需要梯度,于是就无法求梯度。而w和x是我们计算图上的叶子节点,所以必须加上requires_grad=True。
而后面通过w和x延伸定义出的a、b、y,由于依赖的w、x的requires_grad是True,那么a、b、y的这个参数也被默认设置为了True,不需要我们手动添加。
3.叶子节点不可执行in-place操作
计算图上叶子节点处的tensor不能进行原地修改。
什么是in-place操作?
t = torch.tensor([1., 2.])
t.add_(3.)
print(t)
输出
tensor([4., 5.])
torch.Tensor.add_就是torch.add的in-place版本。所谓in-place,就是在tensor上进行原地修改。大部分的torch.tensor的运算,名字后面加一个下划线,就变成inplace操作了。
再比如求绝对值:
t = torch.tensor([-1., -2.])
t.abs_()
print(t)
输出
tensor([1., 2.])
知道什么是in-place操作后,我们尝试一下在requires_grad=True的叶子节点上原地修改,代码如下:
import torchw = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)a = torch.add(w, x)
b = torch.mul(w, x)
y = torch.mul(a, b)w.add_(1)y.backward()
报错信息:
RuntimeError: a leaf Variable that requires grad is being used in an in-place operation.
相关文章:

【Pytorch笔记】4.梯度计算
深度之眼官方账号 - 01-04-mp4-计算图与动态图机制 前置知识:计算图 可以参考我的笔记: 【学习笔记】计算机视觉与深度学习(2.全连接神经网络) 计算图 以这棵计算图为例。这个计算图中,叶子节点为x和w。 import torchw torch.tensor([1.]…...
浏览器安装vue调试工具
下载扩展程序文件 下载链接:链接: 下载连接网盘地址, 提取码: 0u46,里面有两个crx,一个适用于vue2,一个适用于vue3,可根据vue版本选择不同的调试工具 crx安装扩展程序不成功,将文件改为rar文件然后解压 安装…...

C/C++学习 -- RSA算法
概述 RSA算法是一种广泛应用于数据加密与解密的非对称加密算法。它由三位数学家(Rivest、Shamir和Adleman)在1977年提出,因此得名。RSA算法的核心原理是基于大素数的数学问题的难解性,利用两个密钥来完成加密和解密操作。 特点 …...
基于若依ruoyi-nbcio支持flowable流程增加自定义业务表单(一)
因为需要支持自定义业务表单的相关流程,所以需要建立相应的关联表 1、首先先建表wf_custom_form -- ---------------------------- -- Table structure for wf_custom_form -- ---------------------------- DROP TABLE IF EXISTS wf_custom_form; CREATE TABLE wf…...

面试经典 150 题 1 —(数组 / 字符串)— 88. 合并两个有序数组
88. 合并两个有序数组 方法一: class Solution { public:void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {for(int i 0; i<n;i){nums1[mi] nums2[i];}sort(nums1.begin(),nums1.end());} };方法二: clas…...

【大数据 | 综合实践】大数据技术基础综合项目 - 基于GitHub API的数据采集与分析平台
🤵♂️ 个人主页: AI_magician 📡主页地址: 作者简介:CSDN内容合伙人,全栈领域优质创作者。 👨💻景愿:旨在于能和更多的热爱计算机的伙伴一起成长!!&…...
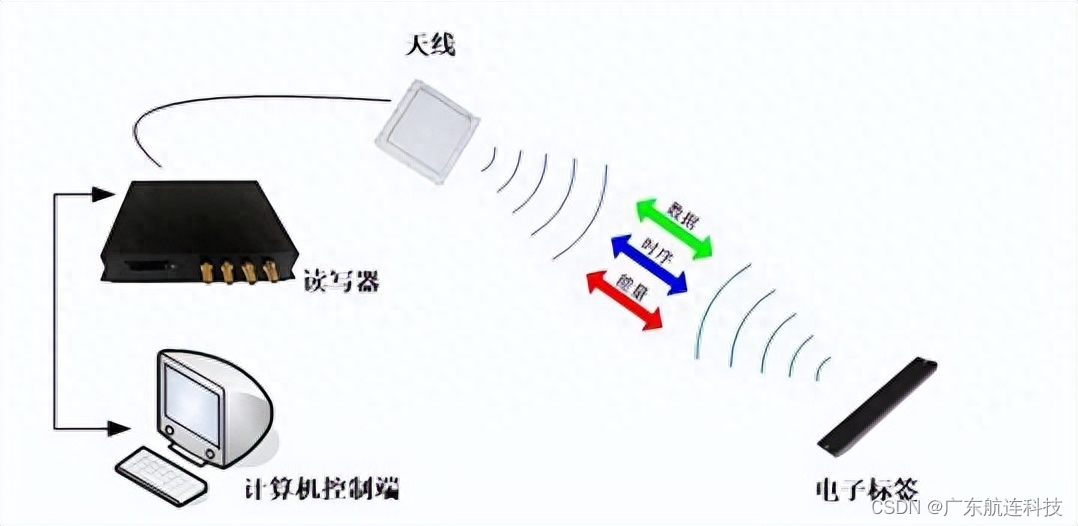
超高频RFID模具精细化生产管理方案
近二十年来,我国的模具行业经历了快速发展的阶段,然而,模具行业作为一个传统、复杂且竞争激烈的行业,企业往往以订单为导向,每个订单都需要进行新产品的开发,从客户需求分析、结构确定、报价、设计、物料准…...

FP-Growth算法全解析:理论基础与实战指导
目录 一、简介什么是频繁项集?什么是关联规则挖掘?FP-Growth算法与传统方法的对比Apriori算法Eclat算法 FP树:心脏部分 二、算法原理FP树的结构构建FP树第一步:扫描数据库并排序第二步:构建树 挖掘频繁项集优化&#x…...

Jmeter 分布式压测,你的系统能否承受高负载?
你可以使用 JMeter 来模拟高并发秒杀场景下的压力测试。这里有一个例子,它模拟了同时有 5000 个用户,循环 10 次的情况。 请求默认配置 token 配置 秒杀接口 结果分析 但是,实际企业中,这种压测方式根本不满足实际需求。下…...

什么是浮动密封?
浮动密封也称为机械面密封或双锥密封,是一种用于各种行业和应用的特殊类型的密封装置。它旨在提供有效的密封和保护,防止污染物的进入以及旋转设备中润滑剂或液体的润滑剂泄漏。 浮动密封件由相同的金属环组成,这些金属环称为密封环…...

浅析前端单元测试
对于前端来说,测试主要是对HTML、CSS、JavaScript进行测试,以确保代码的正常运行。 常见的测试有单元测试、集成测试、端到端(e2e)的测试。 单元测试:对程序中最小可测试单元进行测试。我们可以类比对汽车的测试&…...

线上mysql表字段加不了Fail to get MDL on replica during DDL synchronize,排查记录
某天接近业务高峰期想往表里加字段加不了,报错:Fail to get MDL on replica during DDL synchronize 遂等到业务空闲时操作、还是加不了, 最后怀疑是相关表被锁了,或者有事务一直进行(可能这俩是一个意思)&…...
vue3使用element plus的时候组件显示的是英文
问题截图 这是因为国际化导致的 解决代码 import zhCn from "element-plus/es/locale/lang/zh-cn"; 或者 import zhCn from "element-plus/lib/locale/lang/zh-cn";const localezhCn<el-config-provider :locale"locale"><el-date-pic…...
Matlab参数估计与假设检验(举例解释)
参数估计分为点估计和区间估计,在matlab中可以调用namefit()函数来计算参数的极大似然估计值和置信区间。而数据分析中用得最多的是正态分布参数估计。 例1 从某厂生产的滚珠中抽取10个,测得滚珠的直径(单位:mm)为x[…...

qt响应全局热键
QT5 QWidget响应全局热键-百度经验...

android 代码设置静态Ip地址的方法
在Android中,可以使用以下代码示例来设置静态IP地址: import android.content.Context import android.net.ConnectivityManager import android.net.LinkAddress import android.net.Network import android.net.NetworkCapabilities import android.ne…...
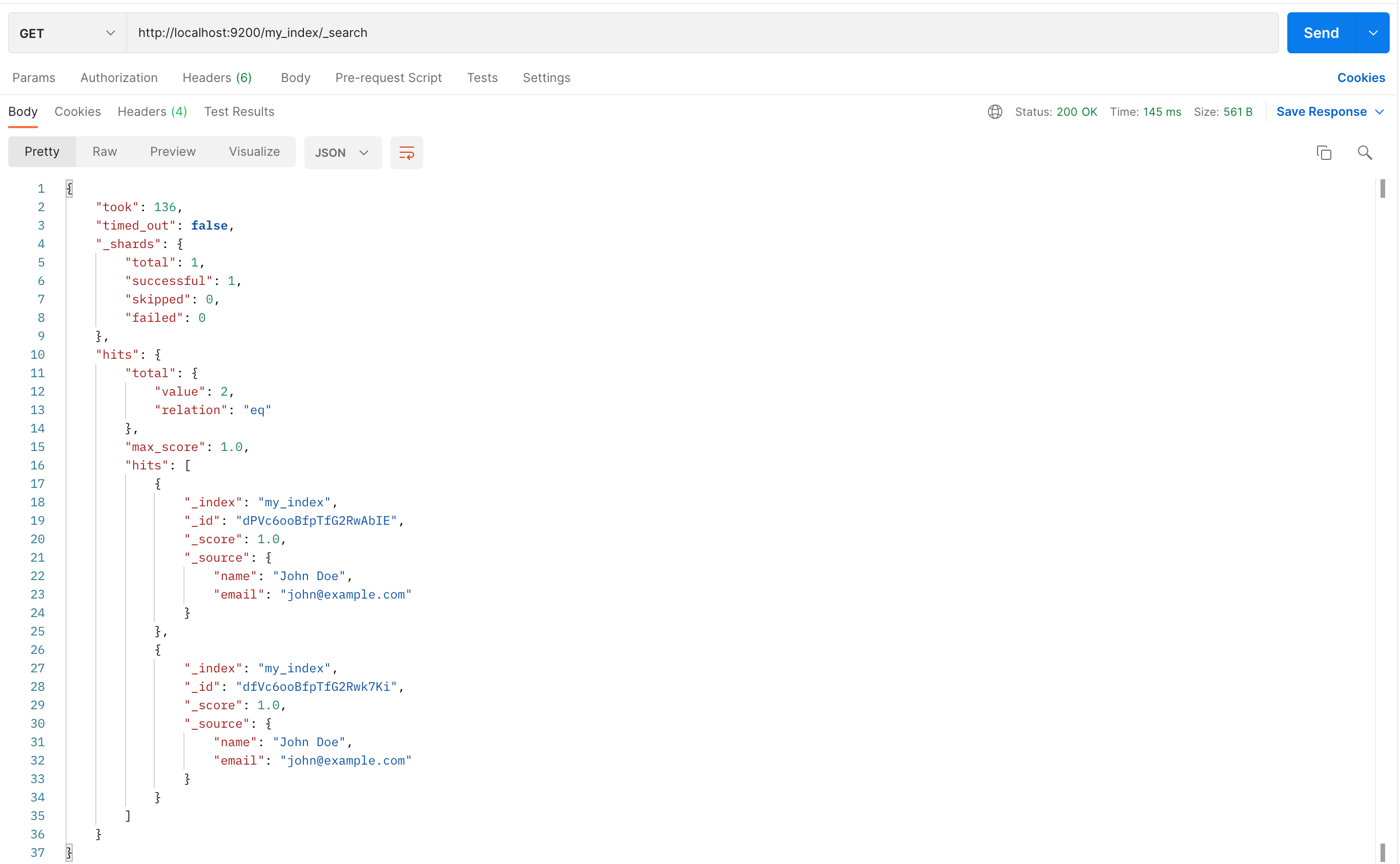
Elasticsearch安装访问
Elasticsearch 是一个开源的、基于 Lucene 的分布式搜索和分析引擎,设计用于云计算环境中,能够实现实时的、可扩展的搜索、分析和探索全文和结构化数据。它具有高度的可扩展性,可以在短时间内搜索和分析大量数据。 Elasticsearch 不仅仅是一个…...
:setState为什么使用异步机制?)
面试题-React(十):setState为什么使用异步机制?
在React中,setState的异步特性和异步渲染机制是开发者们经常讨论的话题。为什么React选择将setState设计为异步操作?异步渲染又是如何实现的?本篇博客将深入探究这些问题,通过代码示例解释为什么异步操作是React的一大亮点。 一、…...
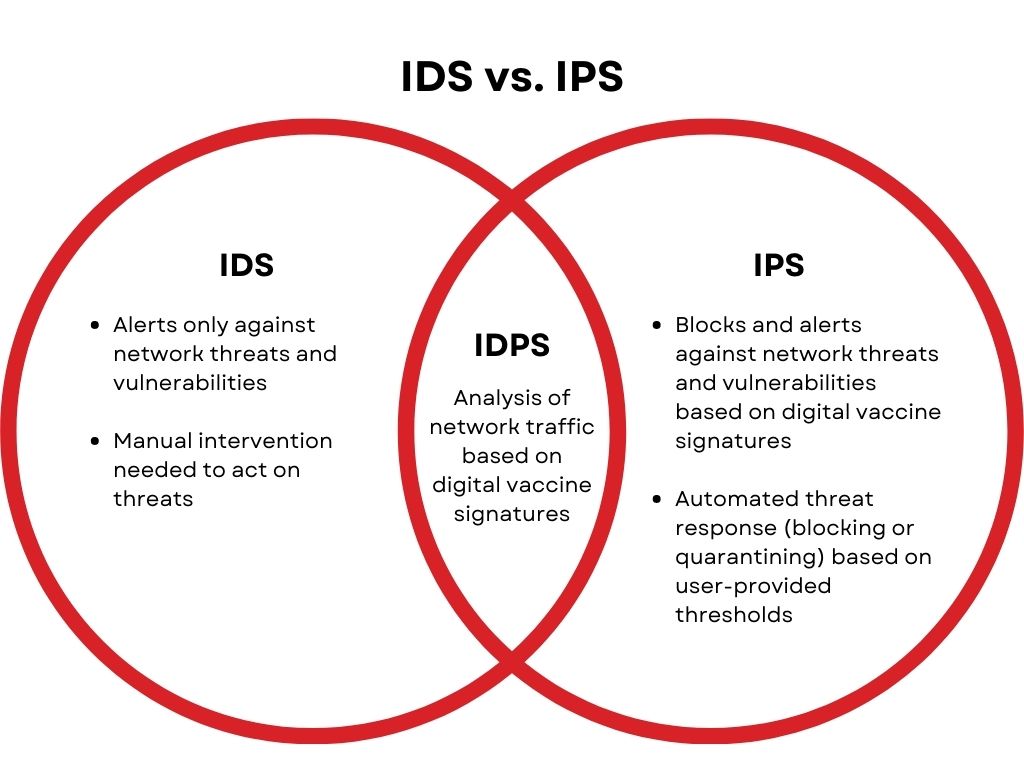
入侵防御系统(IPS)网络安全设备介绍
入侵防御系统(IPS)网络安全设备介绍 1. IPS设备基础 IPS定义 IPS(Intrusion Prevention System)是一种网络安全设备或系统,用于监视、检测和阻止网络上的入侵尝试和恶意活动。它是网络安全架构中的重要组成部分&…...

【Linux基础】Linux的基本指令使用(超详细解析,小白必看系列)
👉系列专栏:【Linux基础】 🙈个人主页:sunnyll 目录 💦 ls 指令 💦 pwd指令 💦cd指令 💦touch指令 💦mkdir指令(重要) 💦rmdir指令…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...
