LeetCode 1277. 统计全为 1 的正方形子矩阵【动态规划】1613
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章中,我不仅会讲解多种解题思路及其优化,还会用多种编程语言实现题解,涉及到通用解法时更将归纳总结出相应的算法模板。
为了方便在PC上运行调试、分享代码文件,我还建立了相关的仓库:https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中,你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等,还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解,还可以一同分享给他人。
由于本系列文章的内容随时可能发生更新变动,欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。
给你一个 m * n 的矩阵,矩阵中的元素不是 0 就是 1,请你统计并返回其中完全由 1 组成的 正方形 子矩阵的个数。
示例 1:
输入:matrix =
[[0,1,1,1],[1,1,1,1],[0,1,1,1]
]
输出:15
解释:
边长为 1 的正方形有 10 个。
边长为 2 的正方形有 4 个。
边长为 3 的正方形有 1 个。
正方形的总数 = 10 + 4 + 1 = 15.
示例 2:
输入:matrix =
[[1,0,1],[1,1,0],[1,1,0]
]
输出:7
解释:
边长为 1 的正方形有 6 个。
边长为 2 的正方形有 1 个。
正方形的总数 = 6 + 1 = 7.
提示:
1 <= arr.length <= 3001 <= arr[0].length <= 3000 <= arr[i][j] <= 1
解法 动态规划/递推(最优)
本题和 221. 最大正方形 非常类似,使用的方法也几乎相同。
我们用 d p [ i ] [ j ] dp[i][j] dp[i][j] 表示以 ( i , j ) (i,j) (i,j) 为右下角的正方形的最大边长,那么除此定义之外, d p [ i ] [ j ] = x dp[i][j] = x dp[i][j]=x 也表示以 ( i , j ) (i,j) (i,j) 为右下角的正方形的数目为 x x x(即边长为 1 , 2 , . . . , x 1, 2, ..., x 1,2,...,x 的正方形各一个)。在计算出所有的 d p [ i ] [ j ] dp[i][j] dp[i][j] 后,我们将它们进行累加,就可以得到矩阵中正方形的数目。
我们尝试挖掘 d p [ i ] [ j ] dp[i][j] dp[i][j] 与相邻位置的关系来计算出 d p [ i ] [ j ] dp[i][j] dp[i][j] 的值。
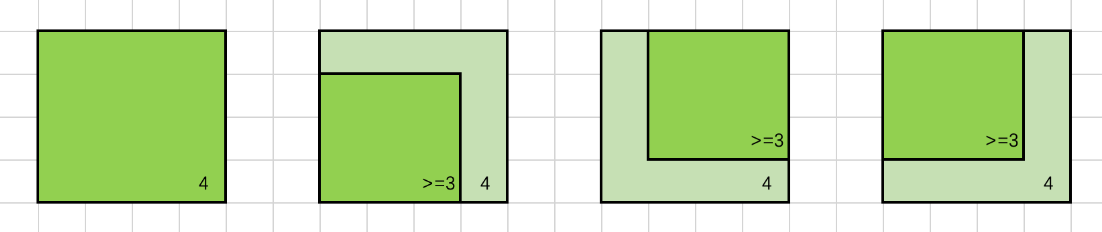
如上图所示,若对于位置 ( i , j ) (i,j) (i,j) 有 d p [ i ] [ j ] = 4 dp[i][j] = 4 dp[i][j]=4 ,我们将以 ( i , j ) (i,j) (i,j) 为右下角、边长为 4 4 4 的正方形涂上色,可以发现其左侧位置 ( i , j − 1 ) (i, j - 1) (i,j−1) ,上方位置 ( i − 1 , j ) (i - 1, j) (i−1,j) 和左上位置 ( i − 1 , j − 1 ) (i - 1, j - 1) (i−1,j−1) 均可以作为一个边长为 4 − 1 = 3 4 - 1 = 3 4−1=3 的正方形的右下角。也就是说,这些位置的的 d p dp dp 值至少为 3 3 3 ,即:
dp[i][j - 1] >= dp[i][j] - 1
dp[i - 1][j] >= dp[i][j] - 1
dp[i - 1][j - 1] >= dp[i][j] - 1
将这三个不等式联立,可以得到:
min ( d p [ i ] [ j − 1 ] , d p [ i − 1 ] [ j ] , d p [ i − 1 ] [ j − 1 ] ) ≥ d p [ i ] [ j ] − 1 \min\big(dp[i][j - 1],\ dp[i - 1][j],\ dp[i - 1][j - 1]\big) \geq dp[i][j] - 1 min(dp[i][j−1], dp[i−1][j], dp[i−1][j−1])≥dp[i][j]−1
这是我们通过固定 d p [ i ] [ j ] dp[i][j] dp[i][j] 的值,判断其相邻位置与之的关系得到的不等式。同理,我们也可以固定 d p [ i ] [ j ] dp[i][j] dp[i][j] 相邻位置的值,得到另外的限制条件。
如上图所示,假设 d p [ i ] [ j − 1 ] dp[i][j - 1] dp[i][j−1] , d p [ i − 1 ] [ j ] dp[i - 1][j] dp[i−1][j] 和 d p [ i − 1 ] [ j − 1 ] dp[i - 1][j - 1] dp[i−1][j−1] 中的最小值为 3 3 3 ,也就是说, ( i , j − 1 ) (i, j - 1) (i,j−1) , ( i − 1 , j ) (i - 1, j) (i−1,j) 和 ( i − 1 , j − 1 ) (i - 1, j - 1) (i−1,j−1) 均可以作为一个边长为 3 3 3 的正方形的右下角。我们将这些边长为 3 3 3 的正方形依次涂上色,可以发现,如果位置 ( i , j ) (i,j) (i,j) 的元素为 1 1 1 ,那么它可以作为一个边长为 4 4 4 的正方形的右下角, d p dp dp 值至少为 4 4 4 ,即:
d p [ i ] [ j ] ≥ min ( f [ i ] [ j − 1 ] , f [ i − 1 ] [ j ] , f [ i − 1 ] [ j − 1 ] ) + 1 dp[i][j] \geq \min\big(f[i][j - 1], f[i - 1][j], f[i - 1][j - 1]\big) + 1 dp[i][j]≥min(f[i][j−1],f[i−1][j],f[i−1][j−1])+1
将其与上一个不等式联立,可以得到:
d p [ i ] [ j ] = min ( d p [ i ] [ j − 1 ] , d p [ i − 1 ] [ j ] , d p [ i − 1 ] [ j − 1 ] ) + 1 dp[i][j] = \min\big(dp[i][j - 1], dp[i - 1][j], dp[i - 1][j - 1]\big) + 1 dp[i][j]=min(dp[i][j−1],dp[i−1][j],dp[i−1][j−1])+1
这样我们就得到了 d p [ i ] [ j ] dp[i][j] dp[i][j] 的递推式。此外还要考虑边界( i = 0 i = 0 i=0 或 j = 0 j = 0 j=0)以及位置 ( i , j ) (i,j) (i,j) 的元素为 0 0 0 的情况。
我们按照行优先的顺序依次计算 d p [ i ] [ j ] dp[i][j] dp[i][j] 的值,就可以得到最终的答案。
class Solution {
public:int countSquares(vector<vector<int>>& matrix) {int m = matrix.size(), n = matrix[0].size();vector<vector<int>> dp(m + 1, vector<int>(n + 1));int ans = 0;for (int i = 0; i < m; ++i) {for (int j = 0; j < n; ++j) {if (matrix[i][j] == 1) {dp[i + 1][j + 1] = 1 + min(dp[i][j], min(dp[i][j + 1], dp[i + 1][j]));ans += dp[i + 1][j + 1];}}}return ans;}
};
由于递推式中 d p [ i ] [ j ] dp[i][j] dp[i][j] 只与本行和上一行的若干个值有关,因此空间复杂度可以优化至 O ( N ) O(N) O(N) 。
class Solution {
public:int countSquares(vector<vector<int>>& matrix) {int m = matrix.size(), n = matrix[0].size();vector<int> dp(n + 1);int ans = 0;int pre = 0, temp = 0;for (int i = 0; i < m; ++i) {for (int j = 0; j < n; ++j) {if (matrix[i][j] == 1) {temp = dp[j + 1];dp[j + 1] = 1 + min(pre, min(dp[j + 1], dp[j]));pre = temp; // pre为dp[i][j]ans += dp[j + 1];} else pre = dp[j + 1], dp[j + 1] = 0; // 注意此时也要记录dp[i][j],并更新dp[i+1][j+1]}}return ans;}
};
复杂度分析:
- 时间复杂度: O ( m n ) O(mn) O(mn)
- 空间复杂度: O ( n ) O(n) O(n)
相关文章:

LeetCode 1277. 统计全为 1 的正方形子矩阵【动态规划】1613
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

测试部门来了个00后卷王之王,老油条感叹真干不过,但是...
都说00后躺平了,但是有一说一,该卷的还是卷。 这不,前段时间我们公司来了个00后,工作都没两年,跳槽到我们公司起薪18K,都快接近我了。后来才知道人家是个卷王,从早干到晚就差搬张床到工位睡觉了…...

360 G800行车记录仪,不使用降压线如何开机,8芯插头的定义。
G800记录仪的插头是这样的,图中标出了线的颜色。其中红色为常电V,黑色为GND负极,黄色为ACC受车是否启动控制。 这个记录仪原装的电源线没有降压功能,所以这里的V是12V。 记录仪内部有电源板,负责将12V降压为5V。 如果…...
vue2踩坑之项目:Swiper轮播图使用
首先安装swiper插件 npm i swiper5 安装出现错误:npm ERR npm ERR! code ERESOLVE npm ERR! ERESOLVE could not resolve npm ERR! npm ERR! While resolving: vue/eslint-config-standard6.1.0 npm ERR! Found: eslint-plugin-vue8.7.1 npm ERR! node_modules/esl…...

python经典百题之分桃子
题目:海滩上有一堆桃子,五只猴子来分。第一只猴子把这堆桃子平均分为五份,多了一个,这只 猴子把多的一个扔入海中,拿走了一份。第二只猴子把剩下的桃子又平均分成五份,又多了 一个,它同样把多的一个扔入海中…...
vscode ssh linux C++ 程序调试
vscode调试c++程序相比vs2022要复杂很多,vs2022可以"一键运行调试",vscode则需要自己配置。 vscode调试程序时,会在当前工作目录产生.vscode 目录, 该目录有两个重要文件launch.json和tasks.json, 下面介绍两种调试方法: 手动调试和自动调试。 手动调试 不管…...

VUE和Angular有哪些区别?
Vue.js和Angular是两个流行的前端JavaScript框架,它们有一些明显的区别,包括以下几个方面: 1、语言和工具链的选择: Vue.js使用HTML、JavaScript和CSS来创建组件,使得它更容易学习,因为它使用了常见的Web…...
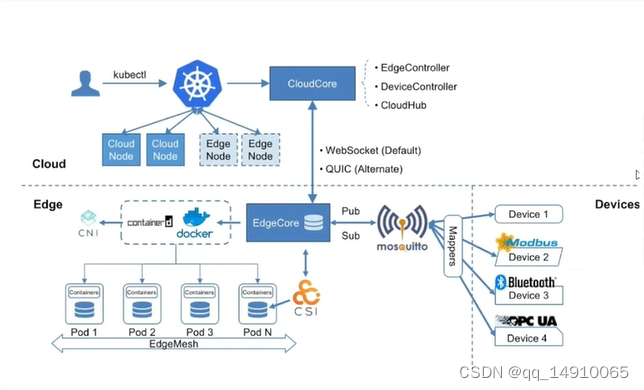
云原生边缘计算KubeEdge安装配置(二)
1. K8S集群部署,可以参考如下博客 请安装k8s集群,centos安装k8s集群 请安装k8s集群,ubuntu安装k8s集群 请安装kubeedge cloudcore centos安装K8S 2.安装kubEedge 2.1 编辑kube-proxy使用ipvs代理 kubectl edit configmaps kube-proxy -…...

SQL多表设计--一对多(外键)
-- 完成部门和员工的-- 选择当前db03 这个数据库use db03;-- 查看当前选中的数据库select database();-- 创建员工表create table tb_emp (id int unsigned primary key auto_increment comment ID,username varchar(20) not null unique comment 用户名,password varchar(32)…...
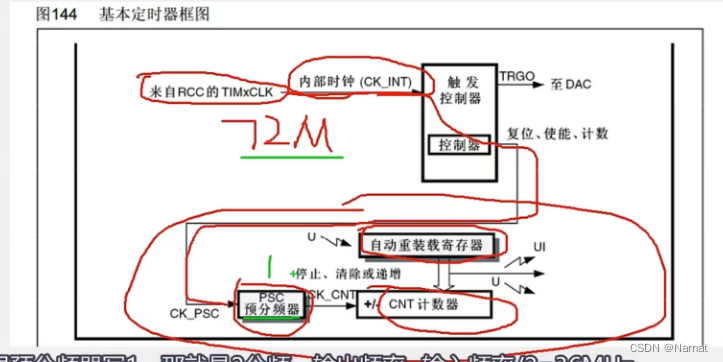
Stm32_标准库_9_TIM
频率(HZ)是频率的基本单位1HZ是1s的倒数 STM32F103C8T6一般情况给定时器的内部时钟都是72MHz(系统主频率) TIM基本构成 计数器、预分频器、自动化重装 // 都是16位其中计数器、自动化重装,都是16位换算成10进制范围为[0, 655536] 时间 1 /…...

283. 移动零
283. 移动零 原题 /** 左指针左边均为非零数; 右指针左边直到左指针处均为零。*/ class Solution {public void moveZeroes(int[] nums) {int left 0;int right 0;while(right<nums.length){if(nums[right]!0){swap(nums,left,right);left;}right;}}public v…...

用 HTTP 提交数据,基本就这 5 种方式
网页开发中,向服务端提交数据是一个基本功能,工作中会大量用 xhr/fetch 的 api 或者 axios 这种封装了一层的库来做。 可能大家都写过很多 http/https 相关的代码,但是又没有梳理下它们有哪几种呢? 其实通过 http/https 向服务端…...
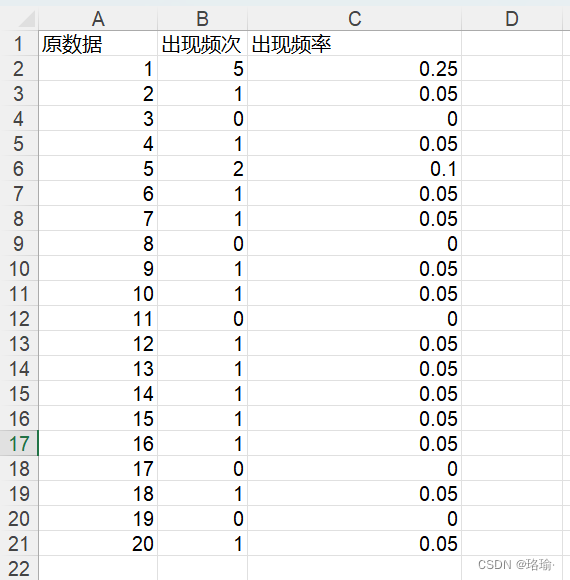
基于matlab统计Excel文件一列数据中每个数字出现的频次和频率
一、需求描述 如上表所示,在excel文件中,有一列数,统计出该列数中,每个数出现的次数和频率。最后,将统计结果输出到新的excel文件中。 二、程序讲解 第一步:选择excel文件; [Filename, Pathn…...
近期分享学习心得3
1、全屏组件封装 先看之前大屏端的监控部分全屏代码 整块全屏代码 常规流是下面这种 //进入全屏 function full(ele) {//if (ele.requestFullscreen) {// ele.requestFullscreen();//} else if (ele.mozRequestFullScreen) {// ele.mozRequestFullScreen();//} el…...
前端uniapp如何修改下拉框uni-data-select下面的uni-icons插件自带的图片【修改uniapp自带源码图片/图标】
目录 未改前图片未改前源码未改前通过top和bottom 和修改后图片转在线base64大功告成最后 未改前图片 未改前源码 然后注释掉插件带的代码,下面要的 未改前通过top和bottom 和修改后 找到uni-icons源码插件里面样式 图片转在线base64 地址 https://the-x.cn/b…...

【计算机基础】Git系列3:常用操作
📢:如果你也对机器人、人工智能感兴趣,看来我们志同道合✨ 📢:不妨浏览一下我的博客主页【https://blog.csdn.net/weixin_51244852】 📢:文章若有幸对你有帮助,可点赞 👍…...
有哪些值得推荐的Java 练手项目?
大家好,我是 jonssonyan 我是一名 Java 后端程序员,偶尔也会写一写前端,主要的技术栈是 JavaSpringBootMySQLRedisVue.js,基于我学过的技术认真的对每个分享的项目进行鉴别,今天就和大家分享我曾经用来学习的开源项目…...
节点)
【Godot】时间线(技能)节点
4.1 游戏中一般都会有各种各样的技能,或者其他需要按一定的时间顺序去执行的功能。 这里我写出了一个时间线节点,就像是在播放动画一样,按一定的阶段去执行某些功能 # # Timeline # # - author: zhangxuetu # - datetime: 2023-09-24 23…...

每日练习-9
目录 1、井字棋 2、密码强度等级 3、二维数组中的查找 4.调整数组奇数偶数 5.旋转数组中的最小元素 6、替换空格 1、井字棋 解析:井字棋有四种情况表示当前玩家获胜,行全为1, 列全为1,主对角全为1, 副对角全为1。遍历…...

微信小程序 -- 页面间通信
前言 今天我们来说下微信小程序的页面间通信: 通过url传参实现页面间单向通信通过getCurrentPages()页面栈实现页面间单向通信通过EventChannel实现页面间双向通信 1、url传参 我们知道页面之间的跳转可以通过路由组件来实现,其中组件的属性url就是要…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...
