算法通过村第十三关-术数|白银笔记|术数高频问题
文章目录
- 前言
- 数组实现加法专题
- 数组实现整数加法
- 字符串加法
- 二进制加法
- 幂运算专题
- 求2的次幂
- 求3的次幂
- 求4的次幂
- 总结
前言
提示:人心本易趋死寂,苦难之后,焕然重建,激荡一阵,又趋麻木。 --苏枕书《有鹿来》
我们继续看几个数学与数字相关的重要题目,数学的问题有很多,力扣上面也有很多练习,通过这些练习你可以掌握很多技巧,真的如果你不练习,你真的不知道其实还可以这么做。所以算法也是一个累计的过程,积累经验才能以后游刃有余。
数组实现加法专题
数字加法,可以说是老生常谈了,但是让你用数组表示一个数,你需要如何去实现呢?今天我们就来挑战一下。
这里提前说一下,你会遇到很多棘手的问题,例如:A[0]位置时发现如果进位要怎么办?
再拓展一下,如果给定两个数,一个数用数组存储,另外一个是普通的整数,又该如何处理呢?
在拓展,如果两个整数是用字符串表示的呢? 如果是二进制表示的呢?加法的规则怎么处理?
数组实现整数加法
参考题目介绍:66. 加一 - 力扣(LeetCode)


这个看似很简单?从后向前一次加就行了,如果有进位就标记一下,但是如果到头了也要进位要怎么办?
例如:digits=[9,9,9],从后面向前加的时候,到了A[0]的位置计算为0,需要再次进位,但是数组却不能保存,这里该怎么办?
这里的关键是A[0] 在什么时候出现进位的情况,我们直到此时一定是9, 99, 999, …这样的结构才会出现加1之后再次进位,而进位之后的结果一定是10,100,1000这样的结构,由于Java中数组默认初始化为0,所以我们此时只需要再次申请一个空间比A[]大一个数的数组B[],然后将B[0]设置为1就可以。代码写起来也很简洁。
/*** 整数加一* @param digits* @return*/public static int[] plusOne(int[] digits) {int len = digits.length;for (int i = len - 1; i >= 0; i--) {digits[i]++;digits[i] %= 10;// 注意这里 提前出去的条件if (digits[i] != 0) {return digits;}}// 9 99 999等 // 这里比较巧妙digits = new int[len + 1];digits[0] = 1;return digits;}
字符串加法
我们继续看将数组存储再字符串中的情况:字符串加法就是使用字符串表示数字,然后计算他们的和。具体要求如下:给定两个字符串形式的非负整数num1和num2,计算他们的和并同样以字符串形式返回。你不能使用内建的用于处理大整数的库(比如BigInteger),也不能直接将输入的字符串转换成整数形式。
我们写个例子:
例如:
输入:num1 = "456" , num2 = "77"
输出:"533"
我们先想一下小学里面的加法是如何实现两个数的计算的。经典的竖式加法:
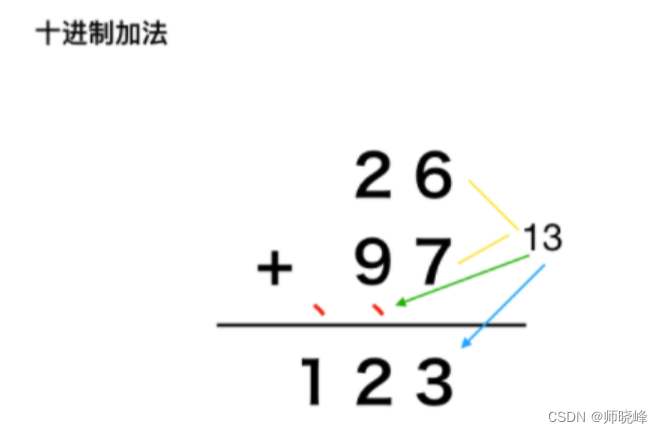
从低位到高位逐步相加,如果当前位和超过10,则向高位进一位。
因此我们只要将这个过程用代码表示出来就可以了。先定义两个指针 i 和 j 分别指向 num1 和num2 的末尾,也就是最低位,同样定义一个变量 add 维护当前是否需要进位,然后从末尾到开头诸位累加。
这里有个问题,两个数字位数不同该怎么处理?很简单,补0就可以了,我们看看具体要怎么做吧:
/*** 两个字符串相加* @param num1* @param num2* @return*/public static String addStrings(String num1, String num2) {// 准备工作int len1 = num1.length(), len2 = num2.length();StringBuffer ans = new StringBuffer();int add = 0;// 注意循环条件处理while(len1 >= 0||len2 >= 0 || add != 0){// 缺位补0int x = len1 >= 0 ? num1.charAt(len1) - '0' : 0;int y = len2 >= 0 ? num2.charAt(len2) - '0' : 0;int result = x + y + add;ans.append(result % 10);add = result / 10;len1--;len2--;}// 计算完毕后记得反转ans.reverse();return ans.toString();}
二进制加法
参考题目介绍:67. 二进制求和 - 力扣(LeetCode)


我们看看二进制怎么处理吧!这个题目也是用字符串表示数据的,也要先转为字符数组。我们熟悉的十进制,是从个位开始,逐步到高位,达到10就进位,而对于二进制判断相加之后是否为2,就可以决定是否发生进位了。如果是就进位。所以思路大致一样,也是由于字符串的操作原因,不确定左后移位是否出现进位,这里提供两个办法处理
- 第一种:在进行计算时直接拼接字符串,得到一个反向字符,最后再翻转回来。(10进制一样)
- 第二种:按照位置给结果字符赋值,最后如果有进位,则在前方进行字符串拼接加进位
我们这里就采用第二种做:
/*** 两个字符串二进制相加* @param a* @param b* @return*/public static String addBinary(String a, String b) {// 准备工作int len1 = a.length(), len2 = b.length();StringBuffer ans = new StringBuffer();int add = 0;for (int i = len1 - 1, j = len2 - 1; i >= 0 || j >= 0; i--, j--) {int sum = add;sum += i >= 0 ? a.charAt(i) - '0' : 0;sum += j >= 0 ? b.charAt(j) - '0' : 0;ans.append(sum % 2);add = sum / 2;}ans.append(add == 1 ? add : "");return ans.reverse().toString();}
当然有人回想,这里转成十进制,计算完成后再转成二进制不也行吗?这么实现很容易,而且可以使用语言的特性直接转换,但是面试的时候也不行,用不了,但是工程里可以这么做,稳定(算法不行,不能这么干)
幂运算专题
幂运算也是常见的数学运算,其形式为ab,也就是a的b次方呗,其中a称为底数,b称为指数,ab的合法运算(不会出现a == 0 且 b <= 0 的情况)。幂运算满足底数和指数都是实数。根据具体情况,底数和指数的数据类型和取值范围也各不相同,例如有的说是,底数是正整数,指数为非负数,有的问题中,底数为实数,指数是整数。
力扣中,幂运算相关的问题主要判断一个数是不是特定正整数的整数次幂,以及快速处理幂。
求2的次幂
参考题目介绍:231. 2 的幂 - 力扣(LeetCode)


本题目的解决思路还是很清晰的,我们可以用除的方法来逐步缩小n的值,另外一个就是使用位运算。
逐步缩小的方法就是:如果n是2的幂数, 则 n > 0,且存在非负整数 k 是的 n = 2 ^ k。
首先判断 n 是否是正整数,如果 n 是 0 或者 负整数,则 n 一定不是 2 的幂。
当 n 是整数时,为了判断 n 是否是 2 的幂, 可以连续对 n 进行除以 2 的操作,直到 n 不能被 2 整除。此时如果 n = 1,那么 n 就是 2 的幂数,否则 n 不是 2 的幂。
代码如下:
/*** 是否为2的幂* @param n* @return*/public static boolean isPowerOfTwo(int n) {if ( n <= 0){return false;}while (n % 2 == 0){n /= 2;}return n == 1;}
当然这种方法效率不高,容易超时。(但是我们有法宝 位运算加强🥰
如果采用位运算,该方法与我们之前说的统计数字转换二进制数以后1的个数思路一致。当 n > 0 时,考虑 n 的二进制表示。如果存在非负整数k 使得 n = 2 ^ k ,则n 的二进制表示为 1 后面跟着 k 个 0 。由此可以看出,正整数 n 是 2 的幂,当且仅当 n 的二进制表示中只有最高位是 1 ,其余位 都是 0, 此时满足 n & ( n - 1) = 0。此时代码就简单多了。
public boolean isPowerOfTwo(int n) {return (n > 0) && (n &(n - 1)) == 0;}
注意:考虑优先级问题
求3的次幂
参考题目介绍:326. 3 的幂 - 力扣(LeetCode)
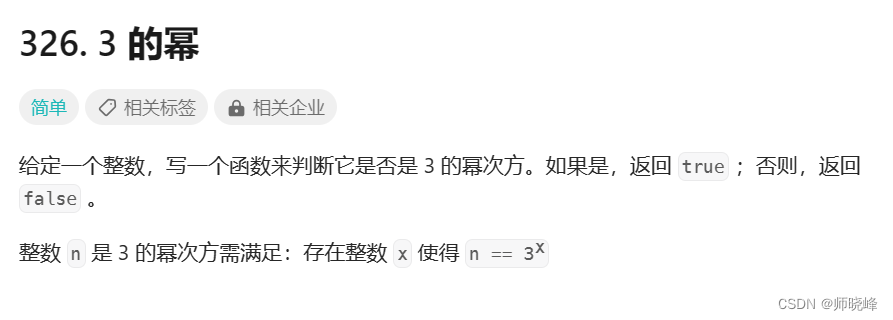

逐步缩小的方法对此也适用:
如果n是 3 的幂数, 则 n > 0,且存在非负整数 k 是的 n = 3 ^ k。
首先判断 n 是否是正整数,如果 n 是 0 或者 负整数,则 n 一定不是 3 的幂。
当 n 是整数时,为了判断 n 是否是 3 的幂, 可以连续对 n 进行除以3 的操作,直到 n 不能被 2 整除。此时如果 n = 1,那么 n 就是 3 的幂数,否则 n 不是 3 的幂。
public boolean isPowerOfThree(int n) {if(n <= 0){return false;}while(n % 3 == 0){n /= 3;}return n == 1;}
这个技巧和上面的一样,这里提供另一个思路:
由于输入 n 是 int 型, 其最大值为 2 ^ 31 - 1。因此在int 型的数据范围内存在最大的 3 的幂,不会超过2 ^ 31 - 1,最大的 3 的幂是 3 ^ 19 = 1162261467。所以在 1 ~ 2 ^ 31 - 1内的数,如果是 3 的幂数,那么一点是1162261467的除数,所以这里就可以这样写:
public boolean isPowerOfThree(int n) {return n > 0 && 1162261467 % n == 0;}
当然这个解法只是扩展思路的,没必要记住这个1162261467这个数字。
思考一下:这里换成4,5,6,7,8,9可以嘛?如果不可以,那如果只是针对素数3,5,7,11, 13 可以嘛?
求4的次幂
参考题目介绍:342. 4的幂 - 力扣(LeetCode)


上述同样的方法这里也可行,推荐换一种判断负数的方式
public boolean isPowerOfFour(int n) {while(n != 0 && n % 4 == 0){n /= 4;}return n == 1;}
试想一下,这个题还能怎么优化,是否可以利用2的次幂呢?
这里留一个作业💕
当然除了幂运算,指数计算的思路与之类似,感兴趣也可以尝试下
50. Pow(x, n) - 力扣(LeetCode)
那这个题练练手
总结
提示:数组加法专题;字符串加法;二进制加法;幂运算;幂运算优化;
如果有帮助到你,请给题解点个赞和收藏,让更多的人看到 ~ ("▔□▔)/
如有不理解的地方,欢迎你在评论区给我留言,我都会逐一回复 ~
也欢迎你 关注我 ,喜欢交朋友,喜欢一起探讨问题。

相关文章:

算法通过村第十三关-术数|白银笔记|术数高频问题
文章目录 前言数组实现加法专题数组实现整数加法字符串加法二进制加法 幂运算专题求2的次幂求3的次幂求4的次幂 总结 前言 提示:人心本易趋死寂,苦难之后,焕然重建,激荡一阵,又趋麻木。 --苏枕书《有鹿来》 我们继续看…...
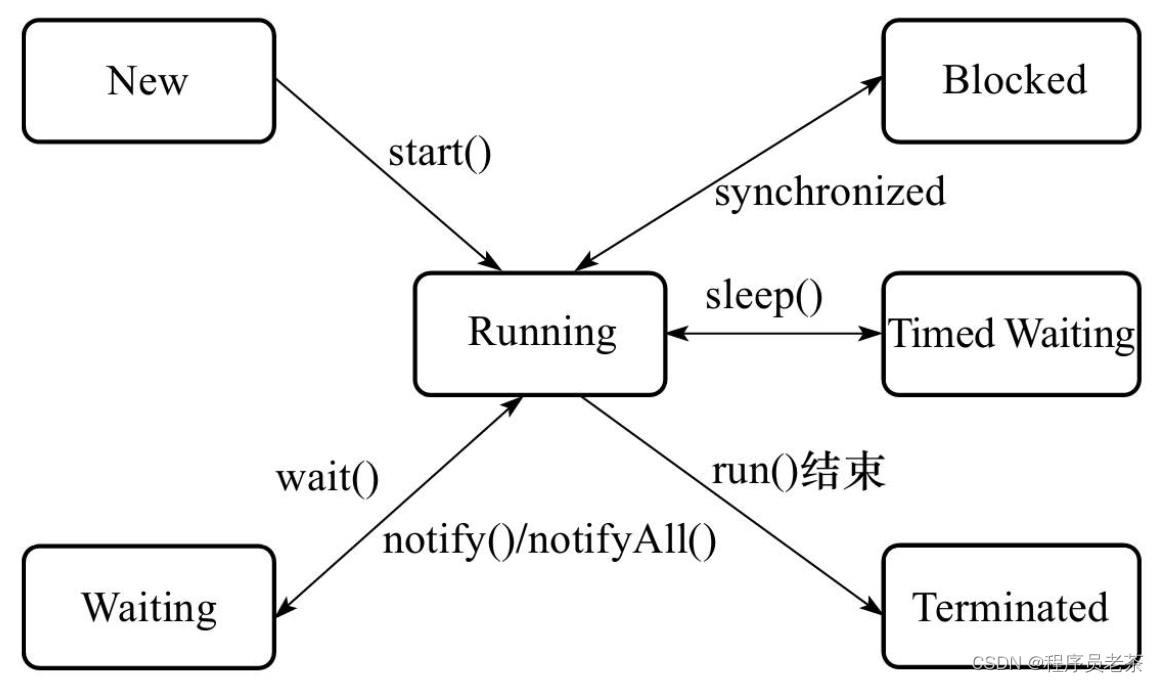
Java 线程的生命周期
🙈作者简介:练习时长两年半的Java up主 🙉个人主页:程序员老茶 🙊 ps:点赞👍是免费的,却可以让写博客的作者开兴好久好久😎 📚系列专栏:Java全栈,…...

Vue页面监听键盘按键的多种方法
在Vue页面中,可以使用多种方法来监听键盘按键。以下是至少五种常用的方法: 使用keydown或keyup指令来绑定键盘按键事件。 <template><div><input type"text" keydown.enter"handleEnterKey" /></div> <…...

解析硬件连通性测试的重要性及测试方法
在现代科技世界中,硬件设备的复杂性和多样性已经达到了前所未有的水平。无论是计算机、智能手机、物联网设备还是嵌入式系统,各种硬件组件的协同工作对于设备的正常运行至关重要。硬件连通性测试是确保这些组件相互配合无误的重要步骤。 一、硬件连通性测…...
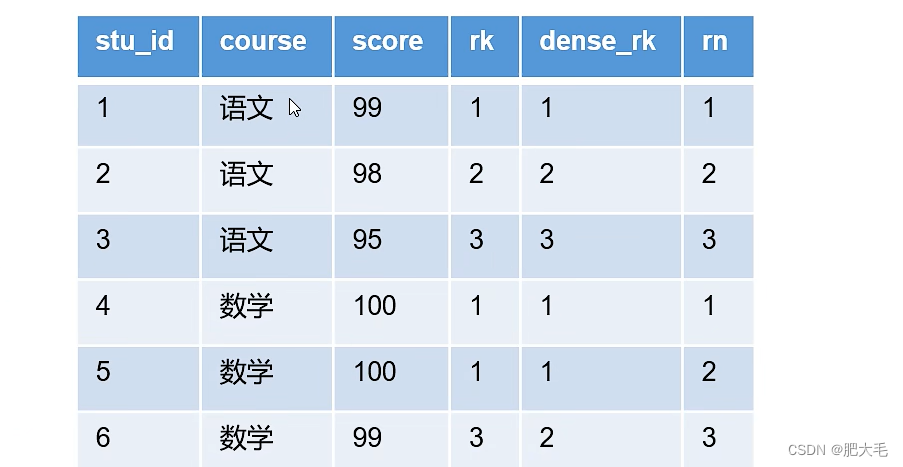
Hive窗口函数回顾
1.语法 1.1 基于行的窗口函数 Hive的窗口函数分为两种类型,一种是基于行的窗口函数,即将某个字段的多行限定为一个范围,对范围内的字段值进行计算,最后将形成的字段拼接在该表上。 注意:在进行窗口函数计算之前&#…...
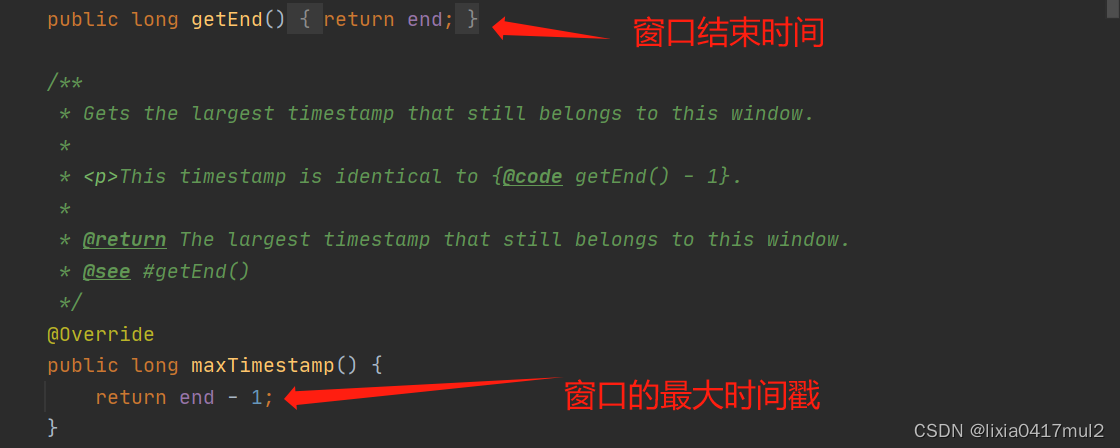
flink自定义窗口分配器
背景 我们知道处理常用的滑动窗口分配器,滚动窗口分配器,全局窗口分配器,会话窗口分配器外,我们可以实现自己的自定义窗口分配器,以实现我们的自己的窗口逻辑 自定义窗口分配器的实现 package wikiedits.assigner;i…...

iOS CGRect CGPoint NSRange等结构体的NSLog打印输出
iOS的UIKit里提供了UIGeometry.h内有各结构体转换成NSString的方法,可用于打印输出; UIKIT_EXTERN NSString *NSStringFromCGPoint(CGPoint point); UIKIT_EXTERN NSString *NSStringFromCGVector(CGVector vector); UIKIT_EXTERN NSString *NSStringFr…...

Viper FTP Mac/ftp管理工具
Viper FTP 是一个用于文件传输和管理的 Mac 应用程序。它允许用户上传、下载和管理远程服务器上的文件,以及在不同本地文件夹之间传输文件。 Viper FTP 支持广泛的文件传输协议,包括 FTP、SFTP、WebDav、Amazon S3、Google Drive 等。它还包括文件同步、…...

web漏洞-xml外部实体注入(XXE)
web漏洞-xml外部实体注入(XXE) 目录 web漏洞-xml外部实体注入(XXE)概念危害检测方法利用方法漏洞利用xxe-lab有回显情况无回显情况 pikachu靶场有回显内容无回显 修复方案 概念 xml可拓展标记语言: xml是一种可拓展的标…...

Impeller-Flutter的新渲染引擎
Impeller是什么?它本质上是怎样运行的? Impeller是Flutter的新的渲染引擎,直到现在Flutter正在用一个叫做Skia的渲染引擎。 问题是Skia不是为了Flutter量身定做的。它有为范围广阔的设备构建的一大堆的渲染特性,这意味着它并不总…...

python 面试算法题
1.第一题 题目描述:给定两个字符串, s 和 goal。如果在若干次旋转操作之后,s 能变成 goal ,那么返回 true 。 s 的 旋转操作 就是将 s 最左边的字符移动到最右边。 例如, 若 s abcde,在旋转一次之后结果就是bcdea 。 示例一: 输入: s &quo…...

Python中的yield关键字
基本概念 yield 是 Python 中的一个关键字,主要在定义生成器函数时使用。使用 yield 的函数在调用时返回一个特殊的迭代器,称为生成器。不同于常规的函数返回一个单一的值(如数字、字符串或其他对象),带有 yield 的函…...
怎么压缩pdf文件?分享缩小pdf文件的简单方法
在我们的日常生活和工作中,往往需要处理大量的PDF文件,而很多时候这些文件的大小会成为传输和存储的难题。为了解决这个问题,下面我们将介绍三种方法来压缩PDF文件,一起来看看吧~ 一、嗨格式压缩大师 首先,最简单也是…...
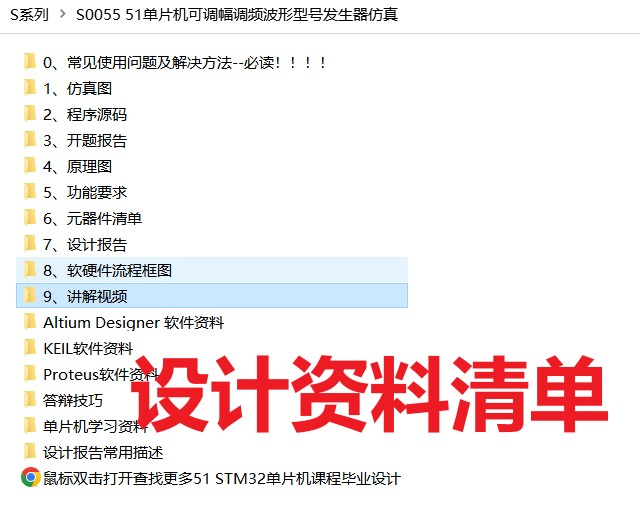
51单片机可调幅度频率波形信号发生器( proteus仿真+程序+原理图+报告+讲解视频)
51单片机可调幅度频率信号发生器( proteus仿真程序原理图报告讲解视频) 讲解视频1.主要功能:2.仿真3. 程序代码4. 原理图4. 设计报告5. 设计资料内容清单&&下载链接***[资料下载链接](https://docs.qq.com/doc/DS1daV1BKRXZMeE9u)*** 51单片机可…...

Vuex的介绍
介绍 :::warning 注意 在阅读此文章之前请确保你已经掌握了组件中的选项 data、计算属性 computed、methods 方法等相关知识。 ::: 什么是 Vuex? Vuex 是一个专为 Vue.js 应用程序开发的状态管理模式。它采用集中式存储管理应用的所有组件的状态,并以…...

mysql基础语法速成版
mysql基础语法速成版 一、前言二、基础语法2.1 数据库操作2.2 MySQL数据类型2.3 表操作2.3.1 表的创建、删除,及表结构的改变2.3.2表数据的增删改查2.3.4 like模糊查询2.3.5 UNION 操作符2.3.6 order by排序2.3.7 group by分组2.3.8 join连接2.3.9 null处理2.3.10 m…...

Docker镜像 配置ssh
安装 1.安装ssh 2.设置root密码 RUN echo root:123456 | chpasswd 3.设置sshd config RUN echo Port 22 >> /etc/ssh/sshd_config RUN echo PermitRootLogin yes >> /etc/ssh/sshd_config4.设置开机启动 RUN mkdir /var/run/sshd #没有这个目录,s…...
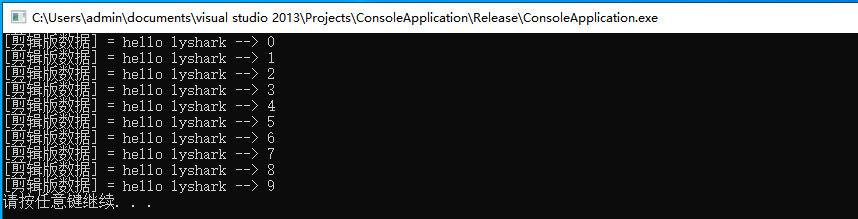
12.2 实现键盘模拟按键
本节将向读者介绍如何使用键盘鼠标操控模拟技术,键盘鼠标操控模拟技术是一种非常实用的技术,可以自动化执行一些重复性的任务,提高工作效率,在Windows系统下,通过使用各种键盘鼠标控制函数实现动态捕捉和模拟特定功能的…...
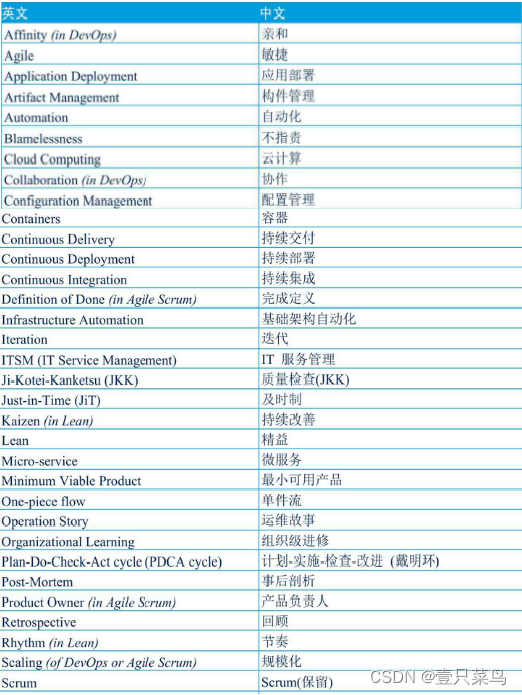
《DevOps 精要:业务视角》- 读书笔记(七)
DevOps 精要:业务视角(七) DevOps历程什么是企业体系的DevOps?DevOps的目标是什么? DevOps的知识体系规范敏捷持续交付IT服务管理以TPS理念为基础 DevOps团队角色流程主管(Process Master)服务主管…...
)
【随想】每日两题Day.12(实则一题)
题目:15. 三数之和 给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请 你返回所有和为 0 且不重复的三元组。 注意:答案中不…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...
