E. Li Hua and Array
Problem - E - Codeforces
思路:观察给定的函数,其实就是求与这个数互质的数的个数,即欧拉函数,我们发现一个数迭代欧拉函数不会很多,那么对于第一个操作来说我们可以直接暴力修改,而对于第二个操作来说,就是求l,r的最近公共祖先,那么我们可以用线段树维护区间的最近公共祖先,并且由于迭代的次数很少,所以并不需要建图,直接暴力跳跃求最近公共祖先即可,那么最总的答案就是用l到r的深度之和-最近公共祖先的深度,乘以区间长度,这就是把这每个点跳跃到最近公共祖先的花费
一定不要建图,建图会MLE
// Problem: E. Li Hua and Array
// Contest: Codeforces - Codeforces Round 864 (Div. 2)
// URL: https://codeforces.com/problemset/problem/1797/E
// Memory Limit: 512 MB
// Time Limit: 3000 ms#include<bits/stdc++.h>
#include<sstream>
#include<cassert>
#define fi first
#define se second
#define i128 __int128
using namespace std;
typedef long long ll;
typedef double db;
typedef pair<int,int> PII;
const double eps=1e-7;
const int N=5e6+7 ,M=6e7+7, INF=0x3f3f3f3f,mod=1e9+7,mod1=998244353;
const long long int llINF=0x3f3f3f3f3f3f3f3f;
inline ll read() {ll x=0,f=1;char c=getchar();while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9') {x=(ll)x*10+c-'0';c=getchar();} return x*f;}
inline void write(ll x) {if(x < 0) {putchar('-'); x = -x;}if(x >= 10) write(x / 10);putchar(x % 10 + '0');}
inline void write(ll x,char ch) {write(x);putchar(ch);}
void stin() {freopen("in_put.txt","r",stdin);freopen("my_out_put.txt","w",stdout);}
bool cmp0(int a,int b) {return a>b;}
template<typename T> T gcd(T a,T b) {return b==0?a:gcd(b,a%b);}
template<typename T> T lcm(T a,T b) {return a*b/gcd(a,b);}
void hack() {printf("\n----------------------------------\n");}int T,hackT;
int n,m,k;
int cost[N];
int pr[3000],cnt;
bool st[3000];
int vis[N];
int depth[N];
struct Node{int l,r;int start;int sum;int add;
};
Node tr[N*4];int lca(int a,int b) {while(a!=b) {if(a>b) a=vis[a];else b=vis[b];}return a;
}void pushup(int u) {tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum;tr[u].add=tr[u<<1].add+tr[u<<1|1].add;tr[u].start=lca(tr[u<<1].start,tr[u<<1|1].start);
}void build(int u,int l,int r) {if(l==r) {if(depth[cost[l]]==0) tr[u]={l,r,cost[l],depth[cost[l]],1};else tr[u]={l,r,cost[l],depth[cost[l]],0};}else {tr[u]={l,r,INF,0,0};int mid=l+r>>1;build(u<<1,l,mid),build(u<<1|1,mid+1,r);pushup(u);}
}void modify(int u,int l,int r) {if(tr[u].r-tr[u].l+1==tr[u].add) return ;if(tr[u].l==tr[u].r) {int tp=vis[tr[u].start];if(depth[tp]==0) tr[u]={tr[u].l,tr[u].r,tp,depth[tp],1};else tr[u]={tr[u].l,tr[u].r,tp,depth[tp],0}; }else {int mid=tr[u].l+tr[u].r>>1;if(l<=mid) modify(u<<1,l,r);if(r>mid) modify(u<<1|1,l,r);pushup(u);}
}int query_sum(int u,int l,int r) {if(tr[u].l>=l&&tr[u].r<=r) return tr[u].sum;else {int mid=tr[u].l+tr[u].r>>1;int res=0;if(l<=mid) res+=query_sum(u<<1,l,r);if(r>mid) res+=query_sum(u<<1|1,l,r);return res;}
}int query_lca(int u,int l,int r) {if(tr[u].l>=l&&tr[u].r<=r) return tr[u].start;else {int mid=tr[u].l+tr[u].r>>1;if(l<=mid&&r>mid) {int a=query_lca(u<<1,l,r);int b=query_lca(u<<1|1,l,r);return lca(a,b);}else if(l<=mid) return query_lca(u<<1,l,r);else return query_lca(u<<1|1,l,r);}
}void get(int x) {int tx=x;int res=x;for(int i=0;i<cnt&&pr[i]<=x/pr[i];i++) {if(x%pr[i]==0) {res=res/pr[i]*(pr[i]-1);while(x%pr[i]==0) x/=pr[i];}}if(x!=1) res=res/x*(x-1);vis[tx]=res;depth[tx]=depth[res]+1;
}void init() {int t=sqrt(5000000);for(int i=2;i<=t;i++) {if(!st[i]) pr[cnt++]=i;for(int j=0;pr[j]<=t/i;j++) {st[pr[j]*i]=true;if(i%pr[j]==0) break;}}depth[1]=0;for(int i=2;i<=5000000;i++) get(i);
}void solve() {n=read(),m=read();for(int i=1;i<=n;i++) cost[i]=read();init();build(1,1,n);while(m--) {int op=read();int l=read(),r=read();if(op==1) {modify(1,l,r);}else if(op==2) {int s=query_lca(1,l,r);int sum=query_sum(1,l,r);printf("%d\n",sum-depth[s]*(r-l+1));}}
} int main() {// init();// stin();// ios::sync_with_stdio(false); // scanf("%d",&T);T=1; while(T--) hackT++,solve();return 0;
}
相关文章:

E. Li Hua and Array
Problem - E - Codeforces 思路:观察给定的函数,其实就是求与这个数互质的数的个数,即欧拉函数,我们发现一个数迭代欧拉函数不会很多,那么对于第一个操作来说我们可以直接暴力修改,而对于第二个操作来说&am…...
【项目】在线oj
1. 创建项目 创建maven项目。 引入依赖(mysql connector和servlet): <dependencies><!-- https://mvnrepository.com/artifact/mysql/mysql-connector-java --><dependency><groupId>mysql</groupId><ar…...

第十章-输入输出系统
Ⅰ.锁 本质是互斥操作 原因:针对公共资源访问时,临界区若不加以互斥限制,可能导致执行过程中突然的中断导致出现异常。 1.互斥过程 设定互斥量M为二值信号量,0/1,P-,V,现有两个进程A、B共同…...
TensorFlow学习:使用官方模型进行图像分类、使用自己的数据对模型进行微调
前言 上一篇文章 TensorFlow案例学习:对服装图像进行分类 中我们跟随官方文档学习了如何进行预处理数据、构建模型、训练模型等。但是对于像我这样的业余玩家来说训练一个模型是非常困难的。所以为什么我们不站在巨人的肩膀上,使用已经训练好了的成熟模…...
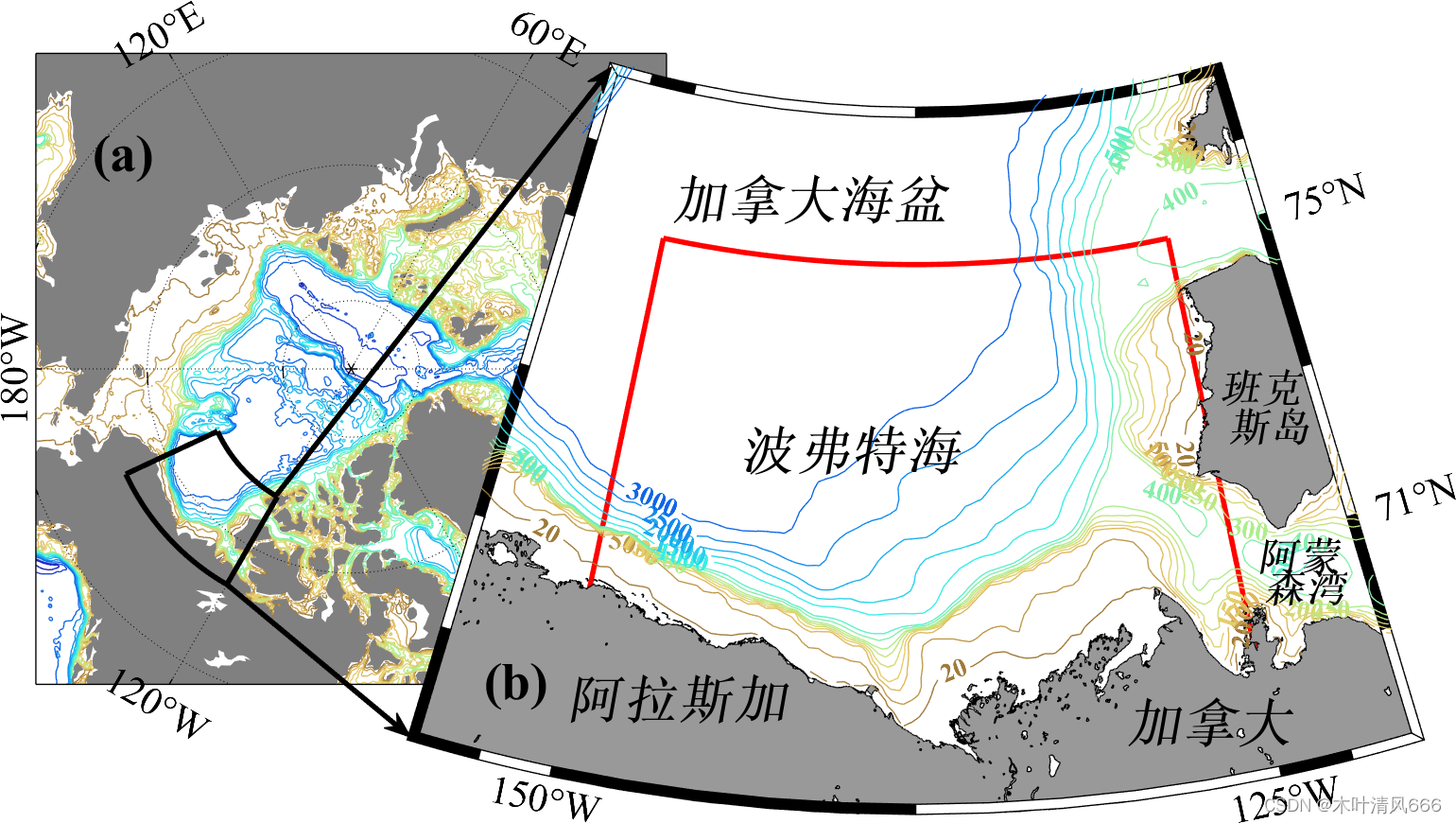
Matlab地理信息绘图—研究区域绘制
文章目录 m_map工具箱Matlab绘制研究区域结果显示 m_map工具箱 m_map是 MATLAB 中用于制作地图和地理数据可视化的工具包。这个工具包提供了一组函数和工具,使得用户能够在 MATLAB 中轻松创建地图,并在地图上显示各种地理和气象数据。以下是 m_map 工具包…...

[CSAWQual 2019]Web_Unagi - 文件上传+XXE注入(XML编码绕过)
[CSAWQual 2019]Web_Unagi 1 解题流程1.1 分析1.2 解题 2 思考总结 1 解题流程 这篇博客讲了xml进行编码转换绕过的原理:https://www.shawroot.cc/156.html 1.1 分析 页面可以上传,上传一句话php失败,点击示例发现是xml格式,那…...
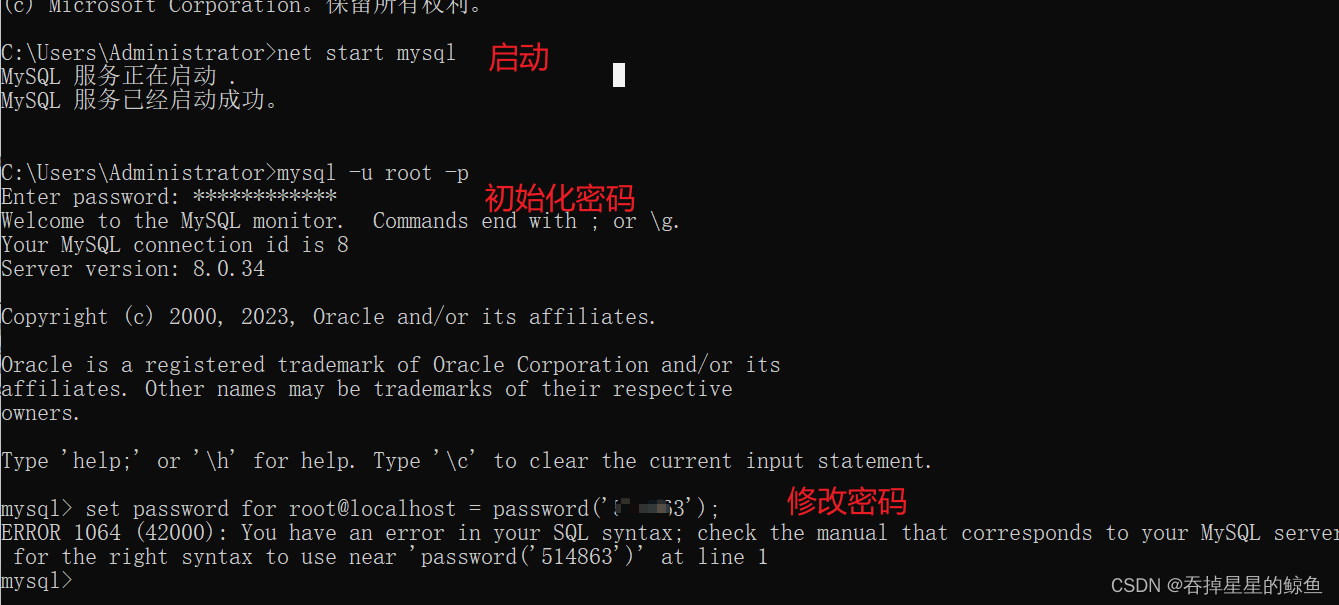
ERROR 2003 (HY000): Can‘t connect to MySQL server on ‘localhost‘ (10061)的问题解决
winR打开窗口输入 services.msc 停止mysql 找到data文件,清空其中全部文件。没有data文件,手动创建 输入 mysqld --remove mysql 移除服务; 注册服务,mysqld -install; 并开始初始化,mysqld --initi…...

什么是函数库和动态链接库?
函数库和动态链接库(也称为共享库)是在软件开发中常见的两种代码重用技术,它们有助于组织、共享和管理代码。在本文中,我们将详细解释函数库和动态链接库的概念、用途以及它们的工作原理。 ## 什么是函数库? 函数库是…...

POM配置
dependencies 所有声明在dependencies里的依赖都会自动引入,并默认被所有的子项目继承 dependencyManagement 只是声明依赖,并不会自动引入,因此子项目需要显示声明依赖。在子项目中声明了依赖项,且没有指定具体版本&#x…...
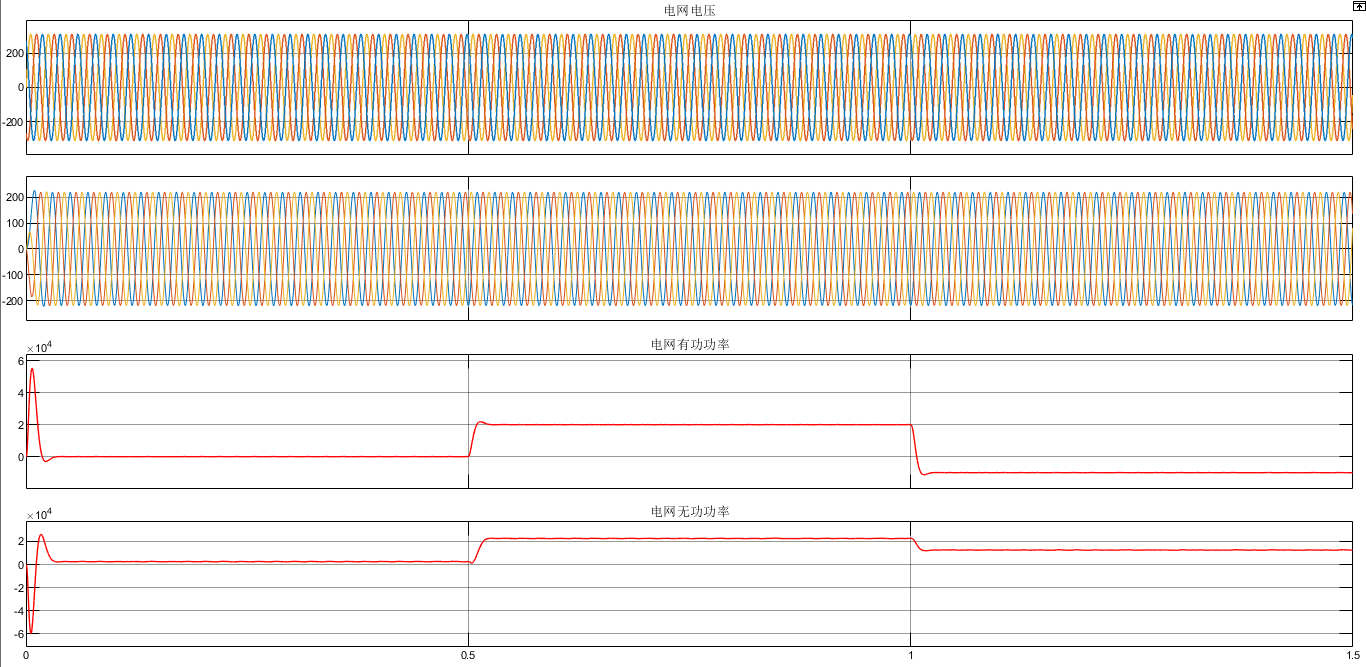
微电网单台并网逆变器PQ控制matlab仿真模型
微❤关注“电气仔推送”获得资料(专享优惠) 微电网运行在并网模式下且公共电网供应正常时,因为公共电网给定了电 压和频率的参考值,所有的逆变器可以使用PQ控制方式。 当系统频率为额定频率f0时,系统稳定在A点&#x…...

计算机毕业设计选什么题目好?springboot 旅游网站
✍✍计算机编程指导师 ⭐⭐个人介绍:自己非常喜欢研究技术问题!专业做Java、Python、微信小程序、安卓、大数据、爬虫、Golang、大屏等实战项目。 ⛽⛽实战项目:有源码或者技术上的问题欢迎在评论区一起讨论交流! ⚡⚡ Java实战 |…...

Android Fragment中使用Arouter跳转到Activity后返回Fragment不回调onActivityResult
Fragment中通过路由跳转到Activity 跳转传递参数 通过Arouter跳转 Postcard postcard ARouter.getInstance().build(RouterConstant.ACTION_TRANSMANAGERACTIVITY1);Bundle bundle new Bundle();bundle.putInt("code", 404);postcard.with(bundle); //设置bundlef…...
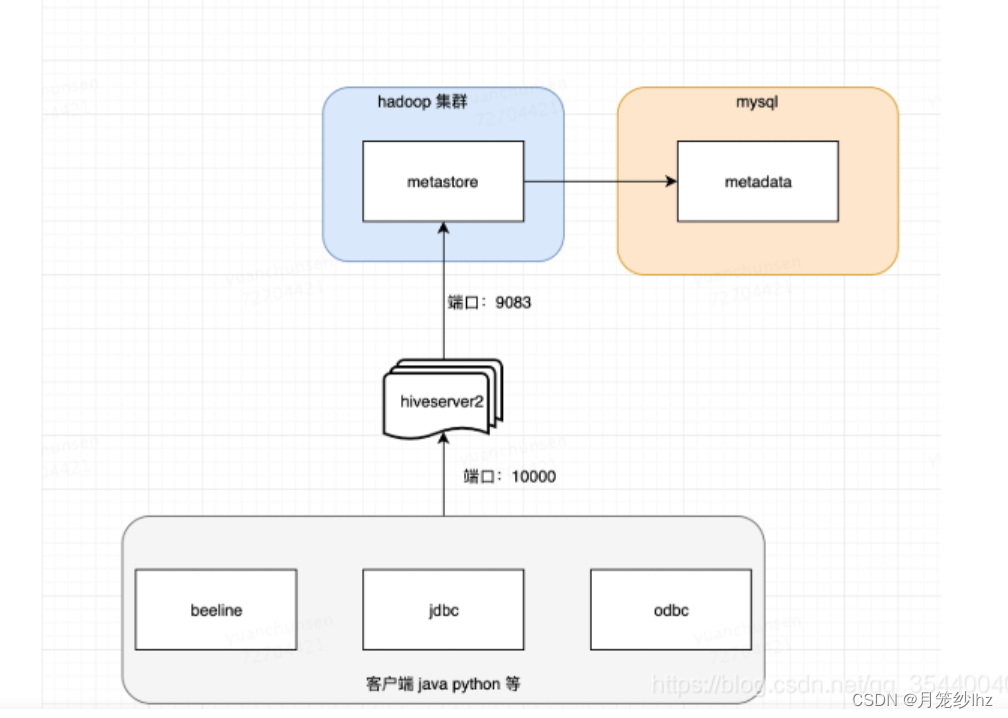
hive add columns 后查询不到新字段数据的问题
分区表add columns 查询不到新增字段数据的问题; 5.1元数据管理 (1)基本架构 Hive的2个重要组件:hiveService2 和metastore,一个负责转成MR进行执行,一个负责元数据服务管理 beeline-->hiveService2/spar…...

【linux】权限相关问题
【linux】权限相关问题 一.用户的分类sudo 二.文件执行的权限i. 文件的分类ii.人的分类三.修改创建文件的权限chmod更改文件创造的默认权限(umask) 三.删除(粘滞位) 一.用户的分类 在我们使用linux的时候,有用户类型的区分,不同用…...
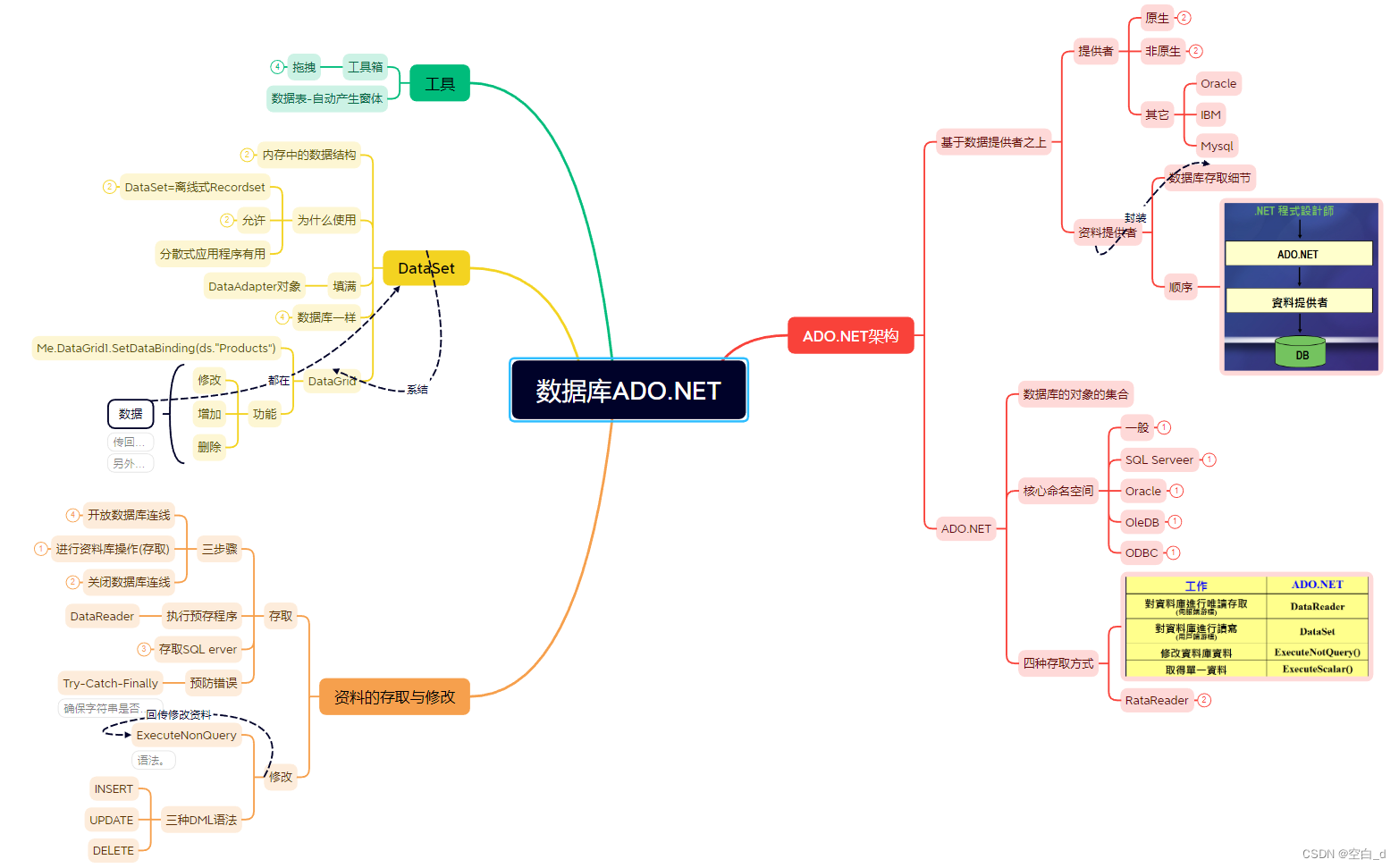
“.NET视频总结:认识框架的结构和组件,掌握开发工具的奥妙“一
目录 第一单元:二十一世纪程序执行 背景: 总结: 第二单元:对象导向与类别设计 背景: 总结: 第三单元:使用类别与基底类别库 总结: 第四单元:Windows开发程序 背景: 总结: 第五单元:防护式程序设计 背景: 总结: 第六…...

02-RocketMQ开发模型
目录汇总:RocketMQ从入门到精通汇总 上一篇:01-RocketMQ整体理解与快速实战 上一部分,我们可以搭建RocketMQ集群,然后也可以用命令行往RocketMQ写入消息并进行消费了。这一部分我们就来看怎么在项目中用上RocketMQ。 一、RocketMQ…...

第83步 时间序列建模实战:Catboost回归建模
基于WIN10的64位系统演示 一、写在前面 这一期,我们介绍Catboost回归。 同样,这里使用这个数据: 《PLoS One》2015年一篇题目为《Comparison of Two Hybrid Models for Forecasting the Incidence of Hemorrhagic Fever with Renal Syndr…...

开源任务调度框架
本文主要介绍一下任务调度框架Flowjob的整体结构,以及整体的心路历程。 功能介绍 flowjob主要用于搭建统一的任务调度平台,方便各个业务方进行接入使用。 项目在设计的时候,考虑了扩展性、稳定性、伸缩性等相关问题,可以作为公司…...
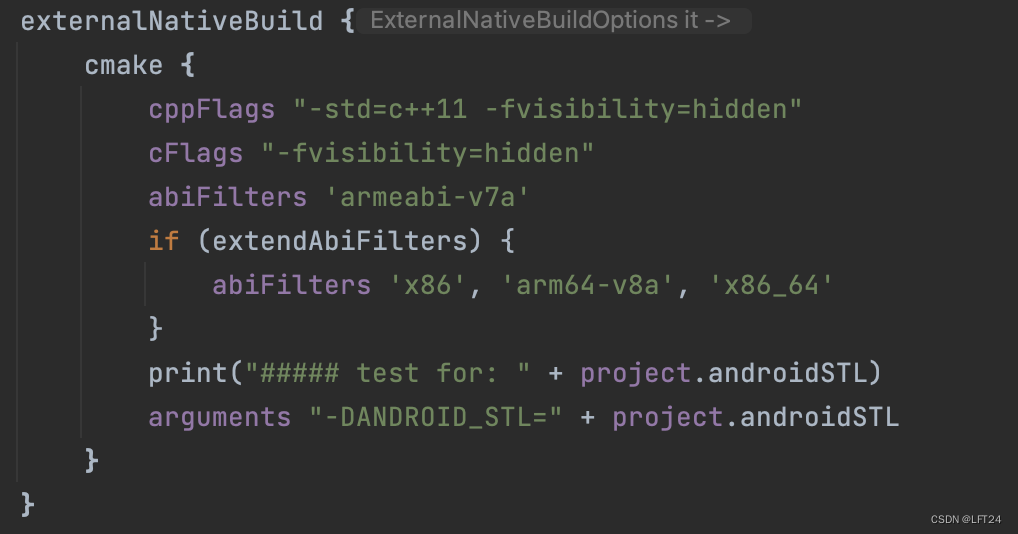
Android Native 开发 要点记录
Android Studio 中写 C 代码 android studio创建C项目_android studio native c-CSDN博客 项目配置参考 【CMake】CMakeLists.txt的超傻瓜手把手教程(附实例源码)_【cmake】cmakelists.txt的超傻瓜手把手教程(附实例源码)-CSDN博客 CMakeLists.txt 讲解…...

数据库中查询所有表信息,查询所有字段信息
MYSQL中 所有表信息 information_schema.tables表 SELECT * FROM information_schema.tables -- TABLE_NAME 表名 -- TABLE_COMMENT 表中文名所有字段信息 information_schema.COLUMNS表 SELECT * FROM information_schema.tables -- TABLE_SCHEMA 数据库名 -- COLUMN…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

Yii2项目自动向GitLab上报Bug
Yii2 项目自动上报Bug 原理 yii2在程序报错时, 会执行指定action, 通过重写ErrorAction, 实现Bug自动提交至GitLab的issue 步骤 配置SiteController中的actions方法 public function actions(){return [error > [class > app\helpers\web\ErrorAction,],];}重写Error…...
