机器学习与模式识别作业----决策树属性划分计算
文章目录
- 1.决策树划分原理
- 1.1.特征选择1--信息增益
- 1.2.特征选择2--信息增益比
- 1.3.特征选择3--基尼系数
- 2.决策树属性划分计算题
- 2.1.信息增益计算
- 2.2.1.属性1的信息增益计算
- 2.2.2.属性2的信息增益计算
- 2.2.3.属性信息增益比较
- 2.2.信息增益比计算
- 2.3.基尼系数计算
1.决策树划分原理
在决策树的算法中,我们常用的划分属性的方法又如下三种:
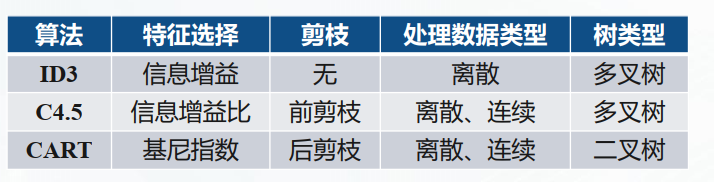
那么我们是怎么通过特征选择指标来进行属性的划分的呢,我们接下来将介绍上述三个特征选择的划分算法。
1.1.特征选择1–信息增益
“信息熵”(information entropy)是度量样本集合纯度最常用的一种指标假定当前样本集合D中第k类样本所占的比例为 p k ( k = 1 , 2 , . . . , ) p_{k}(k = 1,2,...,) pk(k=1,2,...,) ,则D的信息熵定义为
Ent ( D ) = − ∑ k = 1 ∣ Y ∣ p k log 2 p k . \operatorname{Ent}(D)=-\sum_{k=1}^{|\mathcal{Y}|}p_{k}\log_{2}p_{k}. Ent(D)=−k=1∑∣Y∣pklog2pk.
假定离散属性a有V个可能的取值 { a 1 , a 2 , a 3 , . . . . a v } \{{a^{1},a^{2},a^{3},....a^{v}}\} {a1,a2,a3,....av},若使用a来对样本集D进行划分,则会产生V个分支结点,其中第v个分支结点包含了D 中所有在属性a上取值为 a v a^{v} av的样本记为 D v D^{v} Dv,我们可根据计算D信息再考虑到不同的分支结点所包含的样本数不同,给分支结点赋予权重 D v / D D^{v}/D Dv/D即样本数越多的分支结点的影响越大于是可计算出用属性a对样本D进行划分所获得的“信息增益”(information gain)。
G a i n ( D , a ) = E n t ( D ) − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ E n t ( D v ) \mathrm{Gain}(D,a)=\mathrm{Ent}(D)-\sum_{v=1}^{V}\frac{|D^{v}|}{|D|}\mathrm{Ent}(D^{v}) Gain(D,a)=Ent(D)−v=1∑V∣D∣∣Dv∣Ent(Dv)
一般而言,信息增益越大,则意味着使用属性a来进行划分所获得的“纯度提升”越大.因此,我们可用信息增益来进行决策树的划分属性选择。
1.2.特征选择2–信息增益比
实际上,信息增益准则对可取值数目较多的属性有所偏好,为减少这种偏好可能带来的不利影响著名的 C4.5 决策算法不直接使用信息增益而是使用“增益率”(gain ratio)来选择最优划分属性,增益率定义如下所示:
G a i n _ r a t i o ( D , a ) = G a i n ( D , a ) I V ( a ) \mathrm{Gain}\_\mathrm{ratio}(D,a)=\frac{\mathrm{Gain}(D,a)}{\mathrm{IV}(a)} Gain_ratio(D,a)=IV(a)Gain(D,a)
其中,
I V ( a ) = − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ log 2 ∣ D v ∣ ∣ D ∣ \mathrm{IV}(a)=-\sum_{v=1}^{V}\frac{|D^{v}|}{|D|}\log_{2}\frac{|D^{v}|}{|D|} IV(a)=−v=1∑V∣D∣∣Dv∣log2∣D∣∣Dv∣
称为属性a的“固有值”(intrinsic value),属性a的可能取值数目越多(即 V 越大)则IV(a) 的值通常会越大。
需注意的是,增益率准则对可取值数目较少的属性有所偏好,因此,C4.5算法并不是直接选择增益率最大的候选划分属性,而是使用了一个启发式:先从候选划分属性中找出信息增益高于平均水平的属性再从中选择增益率最高的.
1.3.特征选择3–基尼系数
CART决策树使用“基尼指数”(Gini index)来选择划分属性,基尼值的计算公式如下所示:
G i n i ( D ) = ∑ k = 1 ∣ Y ∣ ∑ k ′ ≠ k p k p k ′ = 1 − ∑ k = 1 ∣ Y ∣ p k 2 . \begin{aligned}\mathrm{Gini}(D)&=\sum_{k=1}^{|\mathcal{Y}|}\sum_{k^{\prime}\neq k}p_kp_{k^{\prime}}\\&=1-\sum_{k=1}^{|\mathcal{Y}|}p_k^2.\end{aligned} Gini(D)=k=1∑∣Y∣k′=k∑pkpk′=1−k=1∑∣Y∣pk2.
直观来说,Gini(D)反映了从数据集 D中随机抽取两个样本,其类别标记不一致的概率。因此Gini(D)越小则数据集 D的纯度越高,基尼指数定义如下所示:
G i n i _ i n d e x ( D , a ) = ∑ v = 1 V ∣ D v ∣ ∣ D ∣ . G i n i ( D v ) \mathrm{Gini}\_\mathrm{index}(D,a)=\sum_{v=1}^{V}\frac{|D^{v}|}{|D|.}\mathrm{Gini}(D^{v}) Gini_index(D,a)=v=1∑V∣D∣.∣Dv∣Gini(Dv)
于是,我们在候选属性集合 A 中选择那个使得划分后基尼指数最小的属性作为最优划分属性。
2.决策树属性划分计算题
Iris数据集的某个特征增广版本包含7个样本,具体情况如表格示对比香气和颜色两种特征,分别依据信息增益、 信息增益比和基尼指数给出分裂特征选择结果及计算过程。
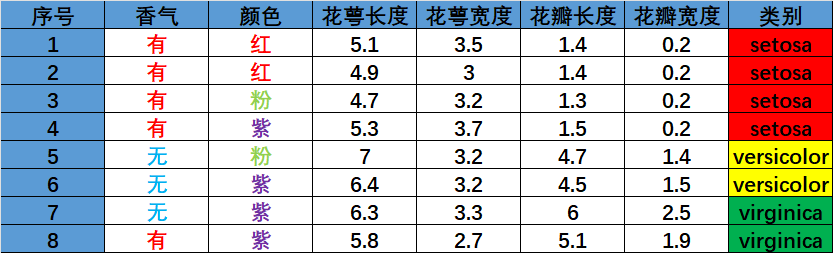
2.1.信息增益计算
2.2.1.属性1的信息增益计算
首先计算根结点的信息熵,根据类别区分出setosa有4朵,versicolor有2朵,virginica有2朵,则根节点的信息熵计算如下:
E n t ( D ) = − ∑ k = 1 3 p k l o g 2 p k = − ( 4 8 l o g 2 4 8 + 2 8 l o g 2 2 8 + 2 8 l o g 2 2 8 ) = 1.5 Ent(D)=-\sum_{k=1}^{3}p_{k}log_{2}p_{k}=-(\frac{4}{8}log_{2}\frac{4}{8}+\frac{2}{8}log_{2}\frac{2}{8}+\frac{2}{8}log_{2}\frac{2}{8} )=1.5 Ent(D)=−k=1∑3pklog2pk=−(84log284+82log282+82log282)=1.5
针对酒香类型,S={有酒香,无酒香},我们分别计算该属性的信息熵如下所示:
E n t ( S 1 ) = − ∑ k = 1 3 p k l o g 2 p k = − ( 4 5 l o g 2 4 5 + 0 l o g 2 0 + 1 5 l o g 2 1 5 ) = 0.721 Ent(S^{1})=-\sum_{k=1}^{3}p_{k}log_{2}p_{k}=-(\frac{4}{5}log_{2}\frac{4}{5}+0log_{2}0+\frac{1}{5}log_{2}\frac{1}{5} )=0.721 Ent(S1)=−k=1∑3pklog2pk=−(54log254+0log20+51log251)=0.721
E n t ( S 2 ) = − ∑ k = 1 3 p k l o g 2 p k = − ( 0 3 l o g 2 0 3 + 2 3 l o g 2 2 3 + 1 3 l o g 2 1 3 ) = 0.918 Ent(S^{2})=-\sum_{k=1}^{3}p_{k}log_{2}p_{k}=-(\frac{0}{3}log_{2}\frac{0}{3}+\frac{2}{3}log_{2}\frac{2}{3}+\frac{1}{3}log_{2}\frac{1}{3} )=0.918 Ent(S2)=−k=1∑3pklog2pk=−(30log230+32log232+31log231)=0.918
最后我们计算酒香属性的信息增益值,如下所示:
Gain ( D , S ) = Ent ( D ) − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ Ent ( D v ) = 1.5 − 5 8 E n t ( D 1 ) − 3 8 E n t ( D 2 ) = 0.705 \operatorname{Gain}(D,S)=\operatorname{Ent}(D)-\sum_{v=1}^V\frac{|D^v|}{|D|}\operatorname{Ent}(D^v)=1.5-\frac{5}{8}Ent(D^{1})-\frac{3}{8}Ent(D^{2})=0.705 Gain(D,S)=Ent(D)−v=1∑V∣D∣∣Dv∣Ent(Dv)=1.5−85Ent(D1)−83Ent(D2)=0.705
2.2.2.属性2的信息增益计算
针对颜色类型,S={红色,粉色,紫色},我们分别计算该属性的信息熵如下所示:
E n t ( S 1 ) = − ∑ k = 1 3 p k l o g 2 p k = − ( 2 2 l o g 2 2 2 + 0 l o g 2 0 ) = 0 Ent(S^{1})=-\sum_{k=1}^{3}p_{k}log_{2}p_{k}=-(\frac{2}{2}log_{2}\frac{2}{2}+0log_{2}0 )=0 Ent(S1)=−k=1∑3pklog2pk=−(22log222+0log20)=0
E n t ( S 2 ) = − ∑ k = 1 3 p k l o g 2 p k = − ( 1 2 l o g 2 1 2 + 1 2 l o g 2 1 2 ) = 1 Ent(S^{2})=-\sum_{k=1}^{3}p_{k}log_{2}p_{k}=-(\frac{1}{2}log_{2}\frac{1}{2}+\frac{1}{2}log_{2} \frac{1}{2})=1 Ent(S2)=−k=1∑3pklog2pk=−(21log221+21log221)=1
E n t ( S 3 ) = − ∑ k = 1 3 p k l o g 2 p k = − ( 1 4 l o g 2 1 4 + 1 2 l o g 2 1 2 + 1 2 l o g 2 1 2 ) = 1.5 Ent(S^{3})=-\sum_{k=1}^{3}p_{k}log_{2}p_{k}=-(\frac{1}{4}log_{2}\frac{1}{4}+\frac{1}{2}log_{2}\frac{1}{2}+ \frac{1}{2}log_{2}\frac{1}{2})=1.5 Ent(S3)=−k=1∑3pklog2pk=−(41log241+21log221+21log221)=1.5
最后我们计算颜色属性的信息增益值,如下所示:
Gain ( D , S ) = Ent ( D ) − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ Ent ( D v ) = 1.5 − 2 8 E n t ( S 1 ) − 2 8 E n t ( S 2 ) − 4 8 E n t ( S 3 ) = 0.5 \operatorname{Gain}(D,S)=\operatorname{Ent}(D)-\sum_{v=1}^V\frac{|D^v|}{|D|}\operatorname{Ent}(D^v)=1.5-\frac{2}{8}Ent(S ^{1})-\frac{2}{8}Ent(S^{2})-\frac{4}{8}Ent(S^{3})=0.5 Gain(D,S)=Ent(D)−v=1∑V∣D∣∣Dv∣Ent(Dv)=1.5−82Ent(S1)−82Ent(S2)−84Ent(S3)=0.5
2.2.3.属性信息增益比较
我们分别求出了酒香和颜色两种属性的信息增益,接下来我们就根据求出的信息增益来划分属性:
Gain ( D , " 酒香 " ) > Gain ( D , " 颜色 " ) \operatorname{Gain}(D,"酒香")>\operatorname{Gain}(D,"颜色") Gain(D,"酒香")>Gain(D,"颜色")
所以我们的选择的属性就是酒香,通过酒香的分类去划分属性。
2.2.信息增益比计算
由上述分析我们知道信息增益和信息增益比的关系,所以我们直接计算信息增益比的值,如下所示:
H ^ { " 酒香 " } = − ∑ k = 1 2 N k N l o g 2 N k N = − ( 5 8 l o g 2 5 8 + 3 8 l o g 2 3 8 ) = 0.954 \hat{H}\{"酒香"\}=-\sum_{k=1}^{2}\frac{N_{k}}{N}log_{2}\frac{N_{k}}{N} =-(\frac{5}{8}log_{2}\frac{5}{8}+\frac{3}{8}log_{2}\frac{3}{8})=0.954 H^{"酒香"}=−k=1∑2NNklog2NNk=−(85log285+83log283)=0.954
H ^ { " 颜色 " } = − ∑ k = 1 2 N k N l o g 2 N k N = − ( 2 8 l o g 2 2 8 + 2 8 l o g 2 2 8 + 4 8 l o g 2 4 8 ) = 1.5 \hat{H}\{"颜色"\}=-\sum_{k=1}^{2}\frac{N_{k}}{N}log_{2}\frac{N_{k}}{N} =-(\frac{2}{8}log_{2}\frac{2}{8}+\frac{2}{8}log_{2}\frac{2}{8}+\frac{4}{8}log_{2}\frac{4}{8})=1.5 H^{"颜色"}=−k=1∑2NNklog2NNk=−(82log282+82log282+84log284)=1.5
由此我们能够计算出对应的信息增益比如下所示:
{ R 1 = G r a i n ( D , " 酒香 " ) H ^ { " 酒香 " } = 0.705 0.954 = 0.738 R 2 = G r a i n ( D , " 颜色 " ) H ^ { " 颜色 " } = 0.5 1.5 = 1 3 \left\{\begin{matrix}R_{1}=\frac{Grain(D,"酒香")}{\hat{H}\{"酒香"\}} =\frac{0.705}{0.954}=0.738 \\R_{2}=\frac{Grain(D,"颜色")}{\hat{H}\{"颜色"\}} =\frac{0.5}{1.5}=\frac{1}{3}\end{matrix}\right. {R1=H^{"酒香"}Grain(D,"酒香")=0.9540.705=0.738R2=H^{"颜色"}Grain(D,"颜色")=1.50.5=31
因为计算出的R1>R2,所以我们的选择的属性就是酒香,通过酒香的分类去划分属性。
2.3.基尼系数计算
Gini系数的计算也比较简答,我们只要根据基尼系数的计算公式来进行计算即可:
计算酒香属性的Gini系数如下所示:
G i n i ( " 香气 " = " 有 " ) = 1 − ∑ 1 2 p k 2 = 1 − ( 4 5 ) 2 − ( 1 5 ) 2 = 0.320 G i n i ( " 香气 " = " 无 " ) = 1 − ∑ 1 2 p k 2 = 1 − ( 1 3 ) 2 − ( 2 3 ) 2 = 0.444 \begin{matrix}Gini("香气"="有")=1-\sum_{1}^{2}p^{2}_{k} =1-(\frac{4}{5} )^{2}-(\frac{1}{5} )^{2}=0.320 \\Gini("香气"="无")=1-\sum_{1}^{2}p^{2}_{k} =1-(\frac{1}{3} )^{2}-(\frac{2}{3} )^{2}=0.444\end{matrix} Gini("香气"="有")=1−∑12pk2=1−(54)2−(51)2=0.320Gini("香气"="无")=1−∑12pk2=1−(31)2−(32)2=0.444
计算颜色属性的Gini系数如下所示:
G i n i ( " 颜色 " = " 红 " ) = 1 − ∑ 1 3 p k 2 = 1 − ( 2 2 ) 2 − 0 − 0 = 0 G i n i ( " 颜色 " = " 粉 " ) = 1 − ∑ 1 3 p k 2 = 1 − ( 1 2 ) 2 − ( 1 2 ) 2 − 0 = 0.5 G i n i ( " 颜色 " = " 紫 " ) = 1 − ∑ 1 3 p k 2 = 1 − ( 1 4 ) 2 − ( 1 4 ) 2 − ( 2 4 ) 2 = 0.625 \begin{matrix}Gini("颜色"="红")=1-\sum_{1}^{3}p^{2}_{k} =1-(\frac{2}{2} )^{2}-0-0=0 \\Gini("颜色"="粉")=1-\sum_{1}^{3}p^{2}_{k} =1-(\frac{1}{2} )^{2}-(\frac{1}{2} )^{2}-0=0.5 \\Gini("颜色"="紫")=1-\sum_{1}^{3}p^{2}_{k} =1-(\frac{1}{4} )^{2}-(\frac{1}{4} )^{2}-(\frac{2}{4} )^{2}=0.625 \end{matrix} Gini("颜色"="红")=1−∑13pk2=1−(22)2−0−0=0Gini("颜色"="粉")=1−∑13pk2=1−(21)2−(21)2−0=0.5Gini("颜色"="紫")=1−∑13pk2=1−(41)2−(41)2−(42)2=0.625
由此我们分别计算对应的基尼系数如下所示:
G i n i _ R a t i o ( " 香气 " ) = 5 8 G i n i 1 + 3 8 G i n i 2 = 0.37 G i n i _ R a t i o ( " 颜色 " ) = 2 8 G i n i 1 + 2 8 G i n i 2 + 4 8 G i n i 3 = 0.437 \begin{matrix}Gini\_Ratio("香气")=\frac{5}{8} Gini_{1}+\frac{3}{8} Gini_{2}=0.37 \\Gini\_Ratio("颜色")=\frac{2}{8} Gini_{1}+\frac{2}{8} Gini_{2}+\frac{4}{8} Gini_{3}=0.437\end{matrix} Gini_Ratio("香气")=85Gini1+83Gini2=0.37Gini_Ratio("颜色")=82Gini1+82Gini2+84Gini3=0.437
因为计算出的 G i n i _ R a t i o ( " 香气 " ) Gini\_Ratio("香气") Gini_Ratio("香气")< G i n i _ R a t i o ( " 颜色 " ) Gini\_Ratio("颜色") Gini_Ratio("颜色"),所以我们的选择的属性就是酒香,通过酒香的分类去划分属性。
相关文章:

机器学习与模式识别作业----决策树属性划分计算
文章目录 1.决策树划分原理1.1.特征选择1--信息增益1.2.特征选择2--信息增益比1.3.特征选择3--基尼系数 2.决策树属性划分计算题2.1.信息增益计算2.2.1.属性1的信息增益计算2.2.2.属性2的信息增益计算2.2.3.属性信息增益比较 2.2.信息增益比计算2.3.基尼系数计算 1.决策树划分原…...
爬虫破解:解决CSRF-Token反爬问题 - 上海市发展和改革委员会
标题:爬虫破解:解决CSRF-Token反爬问题 - 上海市发展和改革委员会 网址:https://fgw.sh.gov.cn/fgw-interaction-front/biz/projectApproval/home MD5加密:ca7f5c978b1809d15a4b228198814253 需求文档 采集数据如下所示: 解决反爬思路 这里只提供解决思路,解决反爬,…...

网络代理技术的威力:保障安全、保护隐私
在如今高度互联的数字时代,网络代理技术正在崭露头角,为网络工程师和普通用户提供了保障网络安全和隐私的强大工具。本文将深入探讨Socks5代理、IP代理以及它们在网络安全、爬虫开发和HTTP协议中的关键作用。 1. Socks5代理:多功能的网络中继…...

【STM32 中断】
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 STM32中断 前言一、STM32的中断如何?如何管理这么复杂的中断?实际优先级如下怎么使用呢? 二、使用步骤1.引入库函数先分组,怎么…...

TensorFlow入门(十二、分布式训练)
1、按照并行方式来分 ①模型并行 假设我们有n张GPU,不同的GPU被输入相同的数据,运行同一个模型的不同部分。 在实际训练过程中,如果遇到模型非常庞大,一张GPU不够存储的情况,可以使用模型并行的分布式训练,把模型的不同部分交给不同的GPU负责。这种方式存在一定的弊端:①这种方…...

在React中,什么是props(属性)?如何向组件传递props?
聚沙成塔每天进步一点点 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 欢迎来到前端入门之旅!感兴趣的可以订阅本专栏哦!这个专栏是为那些对Web开发感兴趣、刚刚踏入前端领域的朋友们量身打造的。无论你是完全的新手还是有一些基础的开发…...

java 每种设计模式的作用,与应用场景
文章目录 前言java 每种设计模式的作用,与应用场景 前言 如果您觉得有用的话,记得给博主点个赞,评论,收藏一键三连啊,写作不易啊^ _ ^。 而且听说点赞的人每天的运气都不会太差,实在白嫖的话࿰…...

Appium问题及解决:打开Appium可视化界面,点击搜索按钮,提示inspectormoved
打开Appium可视化界面,点击搜索按钮,提示inspectorMoved,那么如何解决这个问题呢? 搜索了之后发现,由于高版本Appium(从1.22.0开始)的服务和元素查看器分离,所以还需要下载Appium In…...

android 不同进程之间数据传递
1.handler android.os.Message是定义一个Messge包含必要的描述和属性数据,并且此对象可以被发送给android.os.Handler处理。属性字段:arg1、arg2、what、obj、replyTo等;其中arg1和arg2是用来存放整型数据的;what是用来保存消息标…...

一个完整的初学者指南Django-part1
源自:https://simpleisbetterthancomplex.com/series/2017/09/04/a-complete-beginners-guide-to-django-part-1.html 一个完整的初学者指南Django - 第1部分 介绍 今天我将开始一个关于 Django 基础知识的新系列教程。这是一个完整的 Django 初学者指南。材料分为七…...
SpringBoot和Hibernate——如何提高数据库性能
摘要:本文由葡萄城技术团队发布。转载请注明出处:葡萄城官网,葡萄城为开发者提供专业的开发工具、解决方案和服务,赋能开发者。 前言 在软件开发领域,性能是重中之重。无论您是构建小型 Web 应用程序还是大型企业系统…...
五分钟Win11安装安卓(Android)子系统
十分钟,完成win11安装安卓子系统 Step1、地区设置为美国 Wini 进入设置页面,选择时间和语言-语言和区域- 区域-美国 Step2 安装 Windows Subsystem for Android™ with Amazon Appstore 访问如下连接,install即可 安卓子系统 Step3 安…...
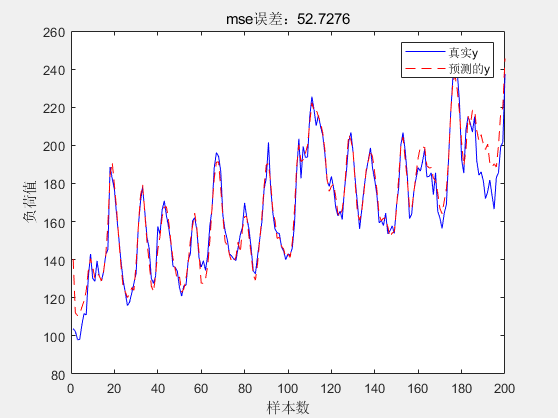
基于LSTM-Adaboost的电力负荷预测的MATLAB程序
微❤关注“电气仔推送”获得资料(专享优惠) 主要内容: LSTM-AdaBoost负荷预测模型先通过 AdaBoost集成算法串行训练多个基学习器并计算每个基学习 器的权重系数,接着将各个基学习器的预测结果进行线性组合,生成最终的预测结果。代码中的LST…...
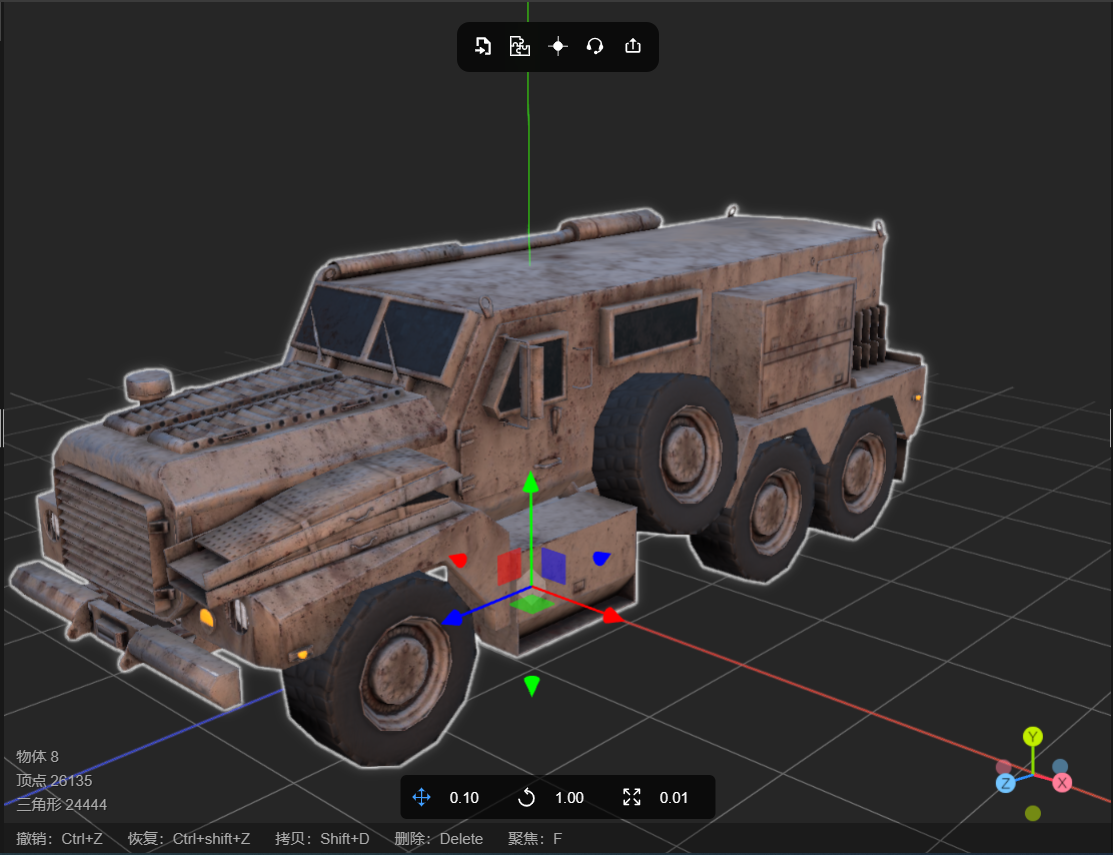
GLTF纹理贴图工具让模型更逼真
1、如何制作逼真的三维模型? 要使三维模型看起来更加逼真,可以考虑以下几个方面: 高质量纹理:使用高分辨率的纹理贴图可以增强模型的细节和真实感。选择适合模型的高质量纹理图像,并确保纹理映射到模型上的UV坐标正确…...
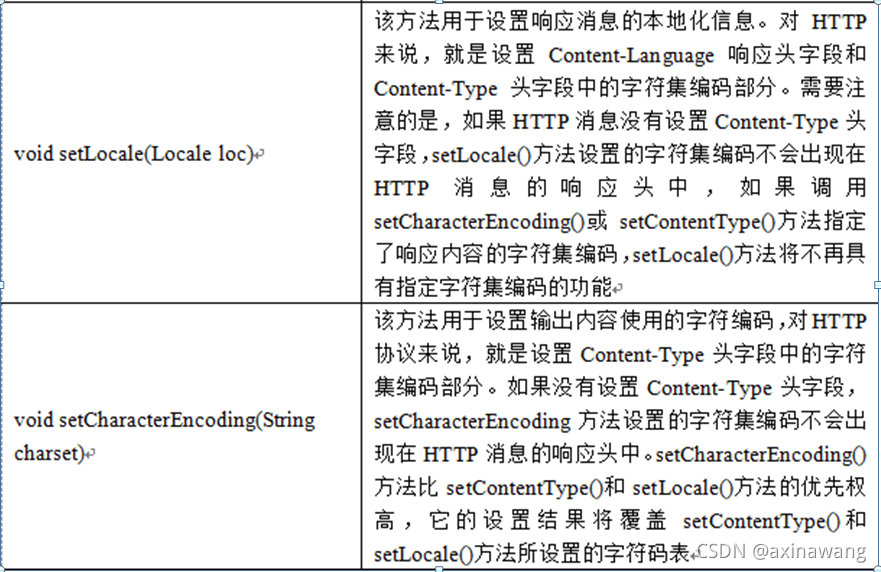
HttpServletResponse对象
1.介绍 在Servlet API中,定义了一个HttpServletResponse接口,它继承自ServletResponse接口,专门用来封装HTTP响应消息。由于HTTP响应消息分为状态行、响应消息头、消息体三部分,因此,在HttpServletResponse接口中定义…...

在SSL中进行交叉熵学习的步骤
在半监督学习(Semi-Supervised Learning,SSL)中进行交叉熵学习通常包括以下步骤: 准备标注数据和未标注数据 首先,你需要准备带有标签的标注数据和没有标签的未标注数据。标注数据通常是在任务中手动标记的ÿ…...
10月TIOBE榜Java跌出前三!要不我转回C#吧
前言 Java又要完了,又要没了,你没看错,10月编程语言榜单出炉,Java跌出前三,并且即将被C#超越,很多资深人士预测只需两个月,Java就会跌出前五。 看到这样的文章,作为一名Java工程师我…...
优盘中毒了怎么办?资料如何恢复
在现代社会中,优盘成为我们日常生活与工作中必备的便携式存储设备。然而,正是由于其便携性,优盘也成为病毒感染的主要目标之一。本篇文章将帮助读者了解如何应对优盘中毒的情况,以及如何恢复因病毒感染丢失的资料。 ▶优盘为什么…...

如何查看端口占用(windows,linux,mac)
如何查看端口占用,各平台 一、背景 如何查看端口占用?网上很多,但大多直接丢出命令,没有任何解释关于如何查看命令的输出 所谓 “查端口占用”,即查看某个端口是否被某个程序占用,如果有,被哪…...
Photoshop与Web技术完美融合,Web版Photoshop已正式登场
通过WebAssembly Emscripten、Web Components Lit、Service Workers Workbox以及对新的Web API的支持,Chrome和Adobe之间的合作使得将Photoshop桌面应用程序引入Web成为了一项重大的里程碑。现在,您可以在浏览器上使用高度复杂和图形密集的软件&#…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...
