机器学习1:k 近邻算法
k近邻算法(k-Nearest Neighbors, k-NN)是一种常用的分类和回归算法。它基于一个简单的假设:如果一个样本的k个最近邻居中大多数属于某一类别,那么该样本也很可能属于这个类别。

k近邻算法的步骤如下:
- 输入:训练集(包含已知类别的样本)和待分类样本。
- 计算待分类样本与训练集中所有样本之间的距离(常用的距离度量方法包括欧氏距离、曼哈顿距离等)。
- 选择距离待分类样本最近的k个样本作为邻居。
- 根据这k个邻居的类别标签,确定待分类样本的类别:如果有多数样本属于A类,那么待分类样本也归为A类;如果多数样本属于B类,那么待分类样本则归为B类。
- 输出:待分类样本的类别。
k近邻算法的主要特点包括:
- 简单易实现:算法主要基于距离计算和多数表决,概念和原理较直观。
- 非参数化学习:算法不对数据的分布做任何假设,因此适用于各种类型的数据。
- 适应性强:算法可以根据具体问题和数据特点选择合适的距离度量方法和邻居个数k。
在实际应用中,可以通过交叉验证等方法选择合适的k值和距离度量方法,以获得更好的分类效果。k近邻算法被广泛应用于模式识别、图像处理、推荐系统等领域。

欧氏距离(Euclidean Distance)是指在数学上计算两个点之间的距离的一种方法。对于二维平面上的两个点,它是通过计算这两个点的坐标差的平方和的平方根得到的。
假设有两个点A(x1, y1)和B(x2, y2),欧氏距离的计算公式如下:
d = sqrt((x2 - x1)^2 + (y2 - y1)^2)
其中,sqrt表示平方根,^ 表示乘方操作。
欧氏距离的特点是:
- 能够度量空间中两点之间的直线距离。
- 距离越小,表示两点越接近;距离越大,表示两点越远离。
- 欧氏距离可以应用于任意维度的数据,不仅仅局限于二维平面。
在机器学习和模式识别等领域,欧氏距离常用于聚类、分类以及特征匹配等任务中,通过比较样本之间的距离来进行相似性度量或分类判定。

曼哈顿距离(Manhattan Distance),也称为城市街区距离或L1距离,是计算两个点之间的距离的一种度量方法。它得名于曼哈顿的城市规划布局,因为在曼哈顿城市街区中,要从一个十字路口到达另一个十字路口,只能沿着网格状的街道走,而不能直线穿越建筑物。
对于二维平面上的两个点A(x1, y1)和B(x2, y2),曼哈顿距离的计算公式如下:
d = |x2 - x1| + |y2 - y1|
其中 |x| 表示取 x 的绝对值。
曼哈顿距离的特点是:
- 它衡量的是沿着网格状路径从一个点到另一个点所需的步数。
- 曼哈顿距离忽略了直线距离,而关注了水平和垂直方向上的距离差异。
- 曼哈顿距离适用于需要考虑路径限制的问题,比如机器人导航、城市交通等领域。
曼哈顿距离不仅可以应用于二维平面,还可以推广到更高维的情况。在机器学习和数据挖掘领域,曼哈顿距离常用于聚类、分类和特征选择等任务中,用于衡量样本之间的相似性或者特征之间的差异。
举例:假设有一个二维坐标系,点A的坐标是(1, 3),点B的坐标是(4, 6)。现在我们要计算点A和点B之间的曼哈顿距离。
曼哈顿距离的计算公式是:d = |x2 - x1| + |y2 - y1|
根据这个公式,我们可以计算出点A和点B之间的曼哈顿距离为:
d = |4 - 1| + |6 - 3| = 3 + 3 = 6
这意味着,从点A移动到点B,沿着水平和垂直方向上的总移动步数是6。可以把曼哈顿距离看作是通过直角路径从一个点到达另一个点所需的最小步数。
将这个理解为在一个城市的街道上行走,曼哈顿距离衡量的是你只能沿着街道走的情况下,从一个地点到另一个地点所需的最短距离。在这个例子中,我们需要向右移动3个单位,向上移动3个单位,即水平方向上的距离差为3,垂直方向上的距离差为3,总步数为6。
棋盘距离(Chebyshev Distance),也称为切比雪夫距离或L∞距离,是计算两个点之间的距离的一种度量方法。它得名于俄罗斯数学家切比雪夫,他首先引入了这个概念。
对于二维平面上的两个点A(x1, y1)和B(x2, y2),
棋盘距离的计算公式如下:d = max(|x2 - x1|, |y2 - y1|)
其中 |x| 表示取 x 的绝对值。
棋盘距离的特点是:
- 它衡量的是沿着网格状路径从一个点到另一个点所需的最少步数。
- 棋盘距离忽略了直线距离,而只考虑水平和垂直方向上的距离差异。
- 棋盘距离适用于仅允许水平、垂直和对角行走的问题,比如在棋盘上移动、机器人导航等领域。
棋盘距离不仅可以应用于二维平面,还可以推广到更高维的情况。在图像处理、路径规划、聚类等领域,棋盘距离常用于衡量像素之间的差异、计算路径的最短距离,或者作为一种距离度量方法进行数据分析和模式识别。
假设我们有一个5x5的棋盘,棋盘上的每个格子表示一个点。现在我们要计算点A(2, 3)和点B(4, 1)之间的棋盘距离。
首先,我们可以通过观察两个点在棋盘上的位置,发现它们可以通过沿着网格状路径移动到达:
在这个路径中,我们可以看到我们需要向右移动两步,向下移动两步,即水平方向上的距离差为2,垂直方向上的距离差也为2。
根据棋盘距离的计算公式 d = max(|x2 - x1|, |y2 - y1|),我们可以取水平方向和垂直方向上距离差的最大值作为最终的棋盘距离。在这个例子中,最大值是2,所以点A和点B之间的棋盘距离就是2。
这个例子展示了棋盘距离的特点,它只考虑水平和垂直方向上的距离差异,并忽略了直线距离。在这个例子中,虽然两点之间的直线距离是√10≈3.16,但棋盘距离只计算了步数,即2步。
综合作业课后题
1. 假设有以下训练数据集,每个样本有两个特征(x1, x2)和对应的类别标签
(y):

现在给定一个测试样本 (6, 4),使用 k 近邻算法进行分类,其中 k=5。请
计算该测试样本的类别。
1) 请简述 k 近邻算法的算法步骤
2) 现在给定一个测试样本 (6, 4),使用 k 近邻算法进行分类,其中 k=5。
分别使用欧氏距离、曼哈顿距离和棋盘距离来计算测试样本与训练样本
之间的距离,并观察它们对最终分类结果的影响。
- k近邻算法的步骤如下:
- 计算测试样本与训练数据集中所有样本之间的距离
- 选择k个距离最近的样本,即为k个邻居
- 根据这k个邻居的类别标签,确定测试样本的类别:如果有多数样本属于A类,那么测试样本也归为A类;如果多数样本属于B类,那么测试样本则归为B类。
2.计算方法及分类结果如下:
使用欧氏距离来计算距离:
样本1:sqrt((3-6)^2 + (5-4)^2) ≈ 3.16,A类
样本2:sqrt((4-6)^2 + (2-4)^2) ≈ 2.83,A类
样本3:sqrt((7-6)^2 + (3-4)^2) ≈ 1.41,B类
样本4:sqrt((9-6)^2 + (6-4)^2) ≈ 3.61,B类
样本5:sqrt((5-6)^2 + (8-4)^2) ≈ 4.12,A类
样本6:sqrt((2-6)^2 + (6-4)^2) ≈ 4.47,B类
从上面的分类结果可以看出,欧氏距离将测试样本分类成了A类。
使用曼哈顿距离来计算距离:
样本1:|3-6| + |5-4| = 4,A类
样本2:|4-6| + |2-4| = 4,A类
样本3:|7-6| + |3-4| = 2,B类
样本4:|9-6| + |6-4| = 5,B类
样本5:|5-6| + |8-4| = 5,A类
样本6:|2-6| + |6-4| = 6,B类
从上面的分类结果可以看出,曼哈顿距离将测试样本分类成了A类。
使用棋盘距离来计算距离:
样本1:max(|3-6|, |5-4|) = 3,A类
样本2:max(|4-6|, |2-4|) = 2,A类
样本3:max(|7-6|, |3-4|) = 1,B类
样本4:max(|9-6|, |6-4|) = 3,B类
样本5:max(|5-6|, |8-4|) = 4,A类
样本6:max(|2-6|, |6-4|) = 4,B类
从上面的分类结果可以看出,棋盘距离也将测试样本分类成了A类。
综上所述,使用这三种距离计算方式,最终测试样本都被归类为A类。
相关文章:

机器学习1:k 近邻算法
k近邻算法(k-Nearest Neighbors, k-NN)是一种常用的分类和回归算法。它基于一个简单的假设:如果一个样本的k个最近邻居中大多数属于某一类别,那么该样本也很可能属于这个类别。 k近邻算法的步骤如下: 输入:…...
知识图谱系列4:neo4j学习
这是一篇还不错的教程,我将会针对其中的Cypher语法在这篇帖子内提出问题,以便学习与复习。 MATCH是什么操作? 小括号()代表什么?(n)代表什么? MATCH (n) DETACH DELETE n是什么含义࿱…...

Mainflux IoT:Go语言轻量级开源物联网平台,支持HTTP、MQTT、WebSocket、CoAP协议
Mainflux是一个由法国的创业公司开发并维护的安全、可扩展的开源物联网平台,使用 Go语言开发、采用微服务的框架。Mainflux支持多种接入设备,包括设备、用户、APP;支持多种协议,包括HTTP、MQTT、WebSocket、CoAP,并支持…...
怎样提取视频中的音频?分享一个一学就会的方法~
每次遇到视频中有好听的背景音乐都会想要保存下来,用于自己的视频创作。于是怎样单独提取视频中的音频部分就成了难题,今天教大家一个简单实用的视频提取音频办法,看完记得点赞收藏哦~ 第一步:打开【音分轨】APP&#…...
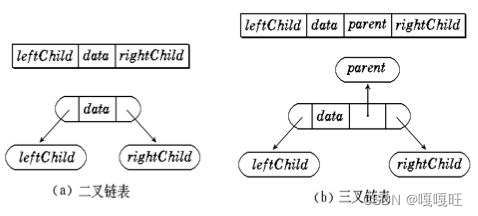
【数据结构】二叉树的基本概念
1.树概念及结构 1.1树的概念 树是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的 子树不能有交集࿰…...

数据可视化实战:如何给毛*易的歌曲做词云展示?
⭐️⭐️⭐️⭐️⭐️欢迎来到我的博客⭐️⭐️⭐️⭐️⭐️ 🐴作者:秋无之地 🐴简介:CSDN爬虫、后端、大数据领域创作者。目前从事python爬虫、后端和大数据等相关工作,主要擅长领域有:爬虫、后端、大数据开发、数据分析等。 🐴欢迎小伙伴们点赞👍🏻、收藏⭐️、…...

智能文本纠错API的崭露头角:革命性的写作辅助工具
前言 在数字化时代,文字是我们日常生活和工作中的不可或缺的一部分。不论是在社交媒体上发帖、撰写商务邮件还是完成学术论文,文字表达都是沟通的核心。然而,字词错误、语法错误和敏感信息却是许多人常常面临的挑战,它们不仅会影…...
-3)
读书笔记:多Transformer的双向编码器表示法(Bert)-3
多Transformer的双向编码器表示法 Bidirectional Encoder Representations from Transformers,即Bert; 第3章 Bert实战 学习如何使用预训练的BERT模型: 如何使用预训练的BERT模型作为特征提取器;探究Hugging Face的Transforme…...

jpsall脚本
当一个集群的节点数量增多时,使用jps查看每一个节点的进程这个过程非常繁琐,因此我们可以写一个jpsall脚本,使用循环迭代的方式,在多台远程主机上执行相同的命令,这样就可以节省在每台主机上手动执行命令的时间和精力。…...
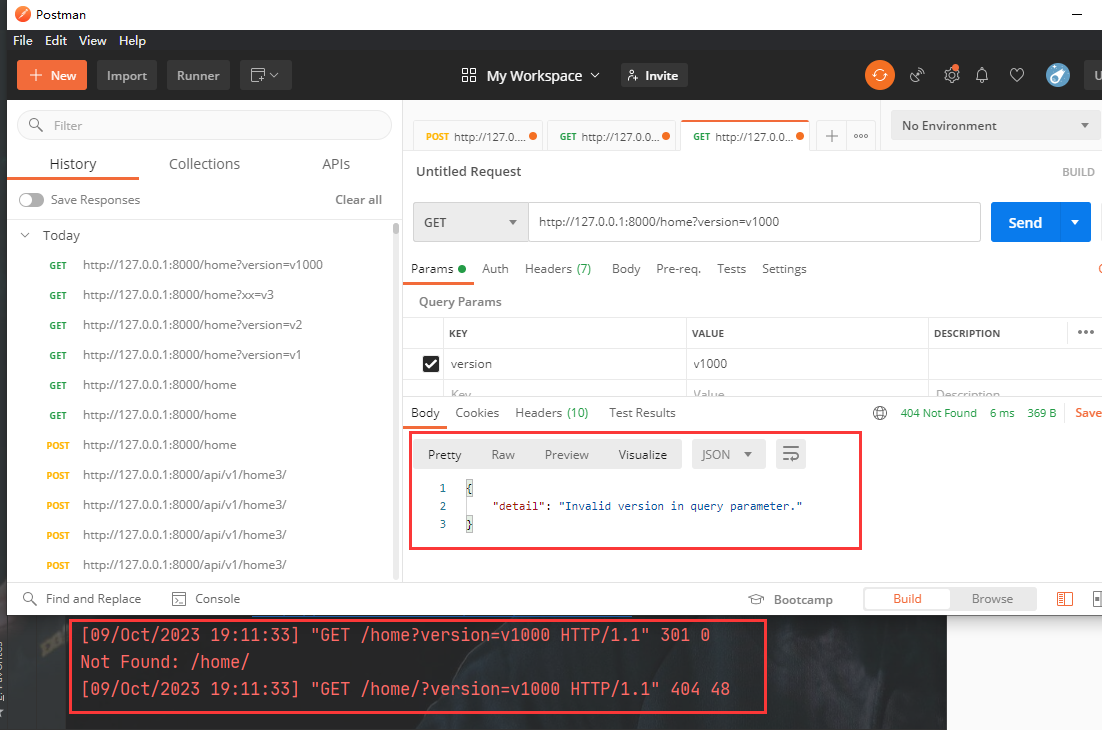
Django REST framework API版本管理【通过GET参数传递】
API版本 在开发过程中可能会有多版本的API,因此需要对API进行管理。django drf中对于版本的管理也很方便。 http://www.example.com/api/v1/info http://www.example.com/api/v2/info 上面这种形式就是很常见的版本管理 在restful规范中,后端的API需…...

归并排序 nO(lgn)
大家好,我是蓝胖子,我一直相信编程是一门实践性的技术,其中算法也不例外,初学者可能往往对它可望而不可及,觉得很难,学了又忘,忘其实是由于没有真正搞懂算法的应用场景,所以我准备出…...
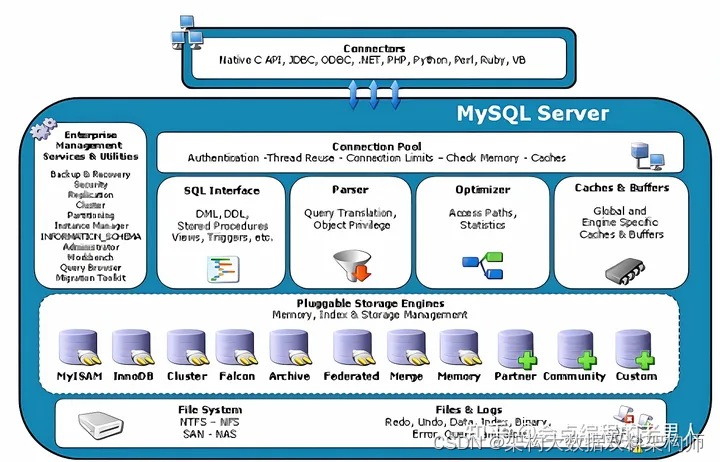
数据库Mysql三大引擎(InnoDB、MyISAM、 Memory)与逻辑架构
MySQL数据库及其分支版本主要的存储引擎有InnoDB、MyISAM、 Memory等。简单地理解,存储引擎就是指表的类型以及表在计算机上的存储方式。存储引擎的概念是MySQL的特色,使用的是一个可插拔存储引擎架构,能够在运行的时候动态加载或者卸载这些存…...
Python数据分析实战-实现Mann-Whitney U检验(附源码和实现效果)
实现功能 使用scipy.stats模块中的mannwhitneyu函数来实现Mann-Whitney U检验,该检验用于比较两个独立样本的分布是否有显著差异。 实现代码 from scipy.stats import mannwhitneyu# 两个独立样本的数据 group1 [1, 2, 3, 4, 5] group2 [6, 7, 8, 9, 10]# 执行…...
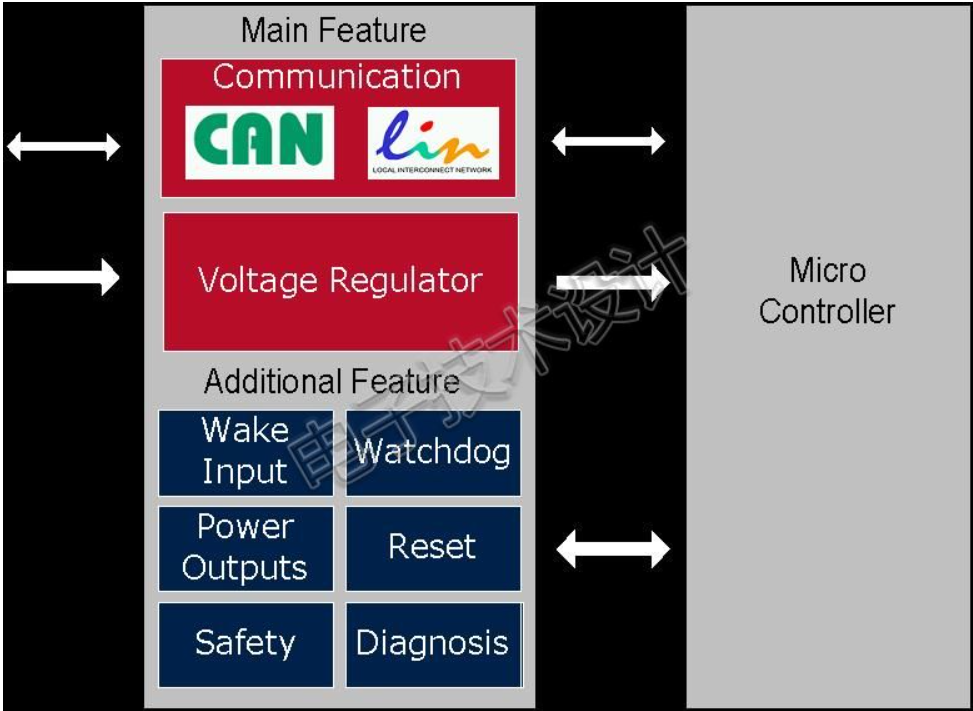
车载SBC芯片概论
+他V hezkz17进数字音频系统研究开发交流答疑群(课题 参考英飞凌SBC官网资料:https://www.infineon.com/cms/cn/product/automotive-system-ic/system-basis-chips-sbc/ SBC芯片在汽车电子领域可谓占一席之地了。那么什么是SBC?怎么用?用在哪里?主要特性? 1.什么是SBC?…...

【ARM AMBA5 CHI 入门 12.1 -- CHI 链路层详细介绍 】
文章目录 CHI 版本介绍1.1 CHI 链路层介绍1.1.1 Flit 切片介绍1.1.2 link layer credit(L-Credit)机制1.1.3 Channel1.1.4 Port1.1. RN Node 接口定义1.1.6 SN Node 接口定义1.2 Channel interface signals1.2.1 Request, REQ, channel1.2.2 Response, RSP, channel1.2.3 Snoop…...

【物联网】Arduino+ESP8266物联网开发(二):控制发光二极管 按钮开关控制开关灯
【物联网】ArduinoESP8266物联网开发(一):开发环境搭建 安装Arduino和驱动 2.ESP8266基础应用 【物联网】ESP8266 开关控制 发光二极管 LED 开发软件下载地址 链接: https://pan.baidu.com/s/1BaOY7kWTvh4Obobj64OHyA?pwd3qv8 提取码: 3qv8 学习过程中会用到的基础…...
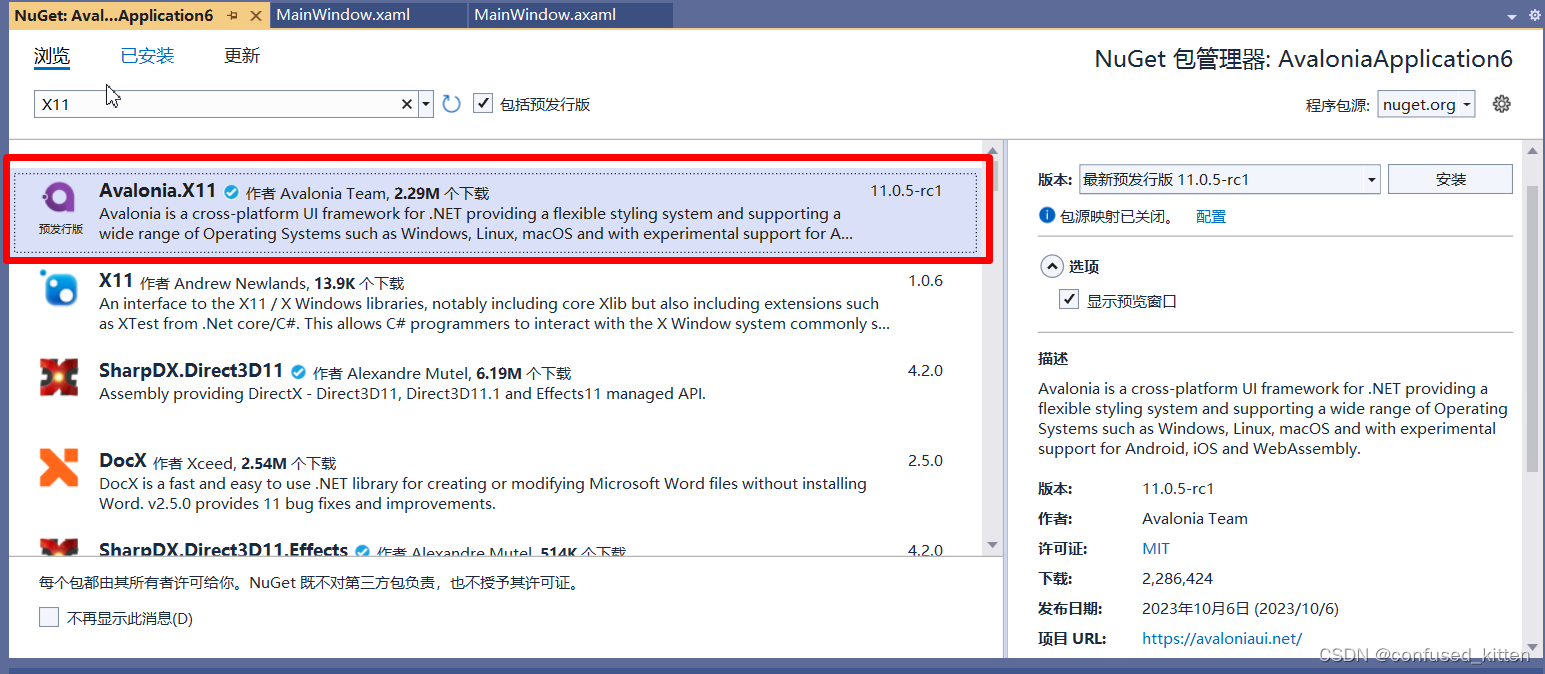
WPF向Avalonia迁移(二、一些可能使用到的库)
可能使用到的一些库 1. UI库 开源项目:https://github.com/irihitech/Semi.Avalonia 如果想引用他的DataGrid样式还需要添加Semi.Avalonia.DataGrid 2. 图表库 LiveChartsCore.SkiaSharpView.Avalonia 3.SVG库 开源项目:https://github.com/wieslaw…...
Mac navicat连接mysql出现1045 - Access denied for user ‘root‘
Mac navicat连接mysql出现1045 - Access denied for user ‘root’ 前提:如果你的mac每次开navicat都连接不上,推荐试试我这个方法 1.打开设置–>找到左下角最下面的MySQL–>点击Stop MySQL Server 2.开启一个终端,依次输入以下命令&a…...
win10电脑插入耳机,右边耳机声音比左边小很多
最近使用笔记本看视频,发现插入耳机(插入式和头戴式)后,右边耳机声音比左边耳机声音小很多很多,几乎是一边很清晰,另一边什么都听不到。 将耳机插到别人电脑上测试耳机正常,那就是电脑的问题。试…...

本文整理了Debian 11在国内的几个软件源。
1.使用说明 一般情况下,将/etc/apt/sources.list文件中Debian默认的软件仓库地址和安全更新仓库地址修改为国内的镜像地址即可,比如将deb.debian.org和security.debian.org改为mirrors.xxx.com,并使用https访问,可使用…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

