OpenCV实现图像傅里叶变换
傅里叶变换
dft=cv.dft(img_float32,flags=cv.DFT_COMPLEX_OUTPUT):
flags:标志位,指定变换类型,cv.DFT_COMPLEX_OUTPUT会返回复数结果。
傅立叶变换,将输入的图像从空间域转换到频率域。
返回结果: 此函数返回一个复杂数值数组,即傅立叶变换的结果。
对于每个像素位置,结果数组中包含两个值:一个实部和一个虚部,这两个值共同构成了一个复数。如果输入的图像是灰度图像,那么结果就是一个二维复数数组。如果输入的是彩色图像,那么结果就是三个二维复数数组(对应于RGB三个通道)。
dft_shift=np.fft.fftshift(dft):
傅立叶变换的结果进行中心移位。在傅立叶变换中,频率是按照从低到高的顺序排列的而在图像中,我们通常更关注中心部分的频率,因此需要将零频率分量(直流分量)移动到频谱的中央。此外,这个函数也用于将频率域的坐标移动到以中心为原点的参考点。
magnitude_spectrum=20*np.log(cv.magnitude(dft_shift[:,:,0],dft_shift[:,:,1]))
dft_shift[:,:,0] 和 dft_shift[:,:,1],这是两个来自前面傅立叶变换步骤的结果,分别代表了傅立叶变换后的实部和虚部计算傅立叶变换结果的幅度谱。20*np.log() 对这个幅度进行对数转换并乘以20,得到的结果就是振幅谱。
import numpy as np
import cv2 as cv
import matplotlib.pyplot as plt
img =cv.imread("../Lena.png",0)
img_float32=np.float32(img)
dft=cv.dft(img_float32,flags=cv.DFT_COMPLEX_OUTPUT)
dft_shift=np.fft.fftshift(dft)magnitude_spectrum=20*np.log(cv.magnitude(dft_shift[:,:,0],dft_shift[:,:,1]))plt.subplot(121)
plt.imshow(img,cmap="gray")
plt.title("Input Image")
plt.xticks([]),plt.yticks([])
plt.subplot(122)
plt.imshow(magnitude_spectrum,cmap="gray")
plt.title("Magnitude Spectrum")
plt.xticks([]),plt.yticks([])
plt.show()
低通滤波和高斯滤波
滤波:
低通滤波器:保留低频,使图片模糊
高通滤波器:保留高频,是图片细节增强
低通滤波:
import numpy as np
import cv2 as cv
import matplotlib.pyplot as pltimg=cv.imread("../Lena.png",0)
img_float=np.float32(img)dft=cv.dft(img_float,flags=cv.DFT_COMPLEX_OUTPUT)
dft_shift=np.fft.fftshift(dft)rows,cols=img.shape
crow,ccol=int(rows/2),int(cols/2) #中心位置#低通滤波
mask=np.zeros((rows,cols,2),np.uint8)
mask[crow-30:crow+30,ccol-30:ccol+30]=1#IDFT
fshift=dft_shift*mask
f_ishift=np.fft.ifftshift(fshift)
img_back=cv.idft(f_ishift)
img_back=cv.magnitude(img_back[:,:,0],img_back[:,:,1])plt.subplot(121)
plt.imshow(img,cmap="gray")
plt.title("Input Image")
plt.xticks([]),plt.yticks([])
plt.subplot(122)
plt.imshow(img_back,cmap="gray")
plt.title("Result")
plt.xticks([]),plt.yticks([])
plt.show()高通滤波
import numpy as np
import cv2 as cv
import matplotlib.pyplot as pltimg=cv.imread("../Lena.png",0)
img_float=np.float32(img)dft=cv.dft(img_float,flags=cv.DFT_COMPLEX_OUTPUT)
dft_shift=np.fft.fftshift(dft)rows,cols=img.shape
crow,ccol=int(rows/2),int(cols/2) #中心位置#高通滤波
mask=np.ones((rows,cols,2),np.uint8)
mask[crow-30:crow+30,ccol-30:ccol+30]=0#IDFT
fshift=dft_shift*mask
f_ishift=np.fft.ifftshift(fshift)
img_back=cv.idft(f_ishift)
img_back=cv.magnitude(img_back[:,:,0],img_back[:,:,1])plt.subplot(121)
plt.imshow(img,cmap="gray")
plt.title("Input Image")
plt.xticks([]),plt.yticks([])
plt.subplot(122)
plt.imshow(img_back,cmap="gray")
plt.title("Result")
plt.xticks([]),plt.yticks([])
plt.show() 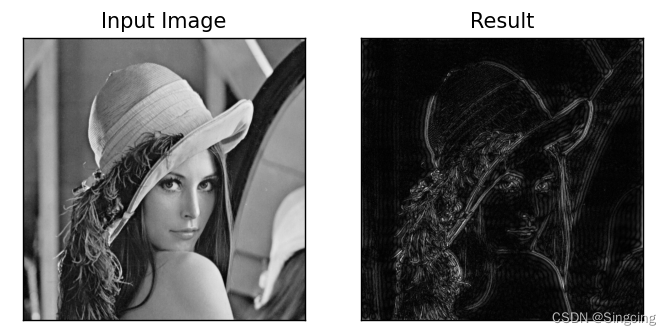
相关文章:

OpenCV实现图像傅里叶变换
傅里叶变换 dftcv.dft(img_float32,flagscv.DFT_COMPLEX_OUTPUT): flags:标志位,指定变换类型,cv.DFT_COMPLEX_OUTPUT会返回复数结果。 傅立叶变换,将输入的图像从空间域转换到频率域。 返回结果: 此函数返回一个复杂数值数组,…...

快手新版本sig3参数算法还原
Frida Native层主动调用 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81…...
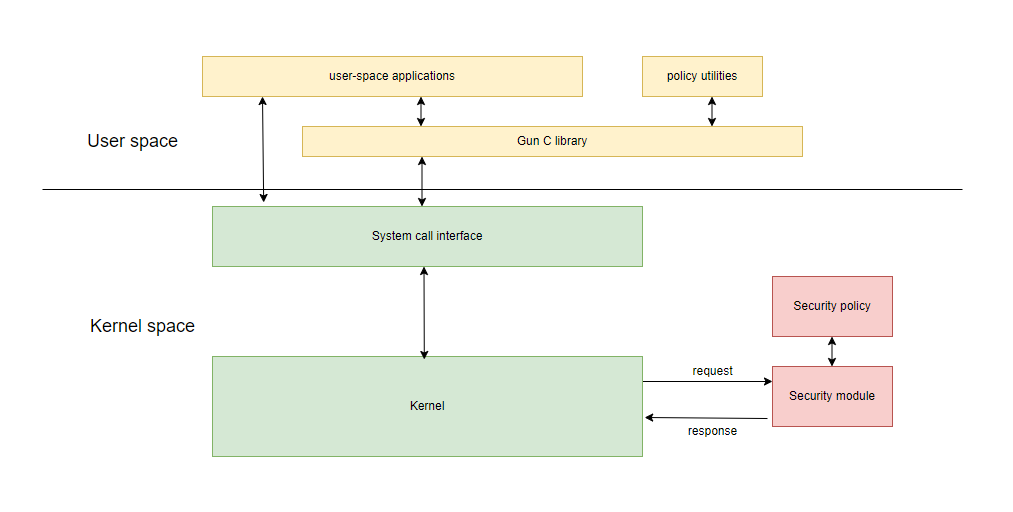
Linux 安全 - LSM机制
文章目录 前言一、LSM起源二、LSM简介2.1 MAC2.2 LSM特征 三、Major and Minor LSMs3.1 Major LSMs3.2 Minor LSMs3.3 BPF LSM 四、LSM 框架五、LSM Capabilities Module六、LSM hooks 说明参考资料 前言 在这两篇文章中介绍了 Linux 安全机制 Credentials : Linu…...
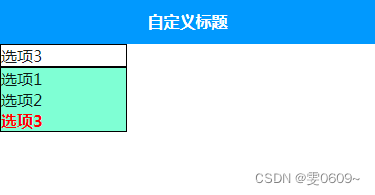
uni-app:实现简易自定义下拉列表
效果 代码 <template><view><view class"dropdown-trigger" tap"showDropdown">{{ selectedItem }}</view><view class"dropdown-list" v-if"showList"><view class"dropdown-item" v-f…...
排序算法——直接插入排序
一、介绍 插入排序就是将前两个元素排好,再将第三个元素通过与前边的元素比较后插入适当的位置,再将第四个元素插入,不断重复插入与前边元素比较的操作,直到将元素都排列好。 演示如下: 视频演示:…...
手动抄表和自动抄表优缺点对比
随着科技的发展,自动抄表技术已经越来越成熟,被广泛应用于各个领域。然而,手动抄表在一些特定场景下仍然具有一定的优势。本文将从手动抄表和自动抄表的优缺点入手,对比分析它们的应用场景和使用价值。 1.成本低:手动抄…...
HiSilicon352 android9.0 emmc添加新分区
添加新分区 从emmc中单独划分出一个分区,用来存储相关数据(可用于存储照片,视频,音乐和文档等)或者系统日志log,从而不影响到其他分区。 实现方法: device/hisilicon/Hi3751V350/etc/Hi3751V3…...
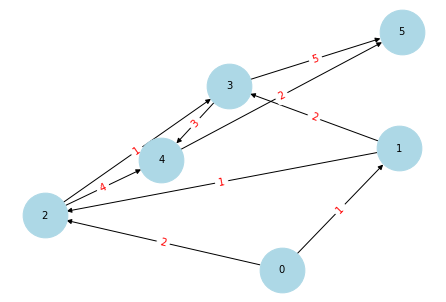
networkX-04-查找k短路
文章目录 1.构建图2.使用networkX查找最短路径3.自己构建方法 教程仓库地址:github networkx_tutorial import networkx as nx import matplotlib.pyplot as plt1.构建图 # 创建有向图 G nx.DiGraph()# 添加带权重的边 edges [(0, 1, 1), (0, 2, 2), (1, 2, 1), …...
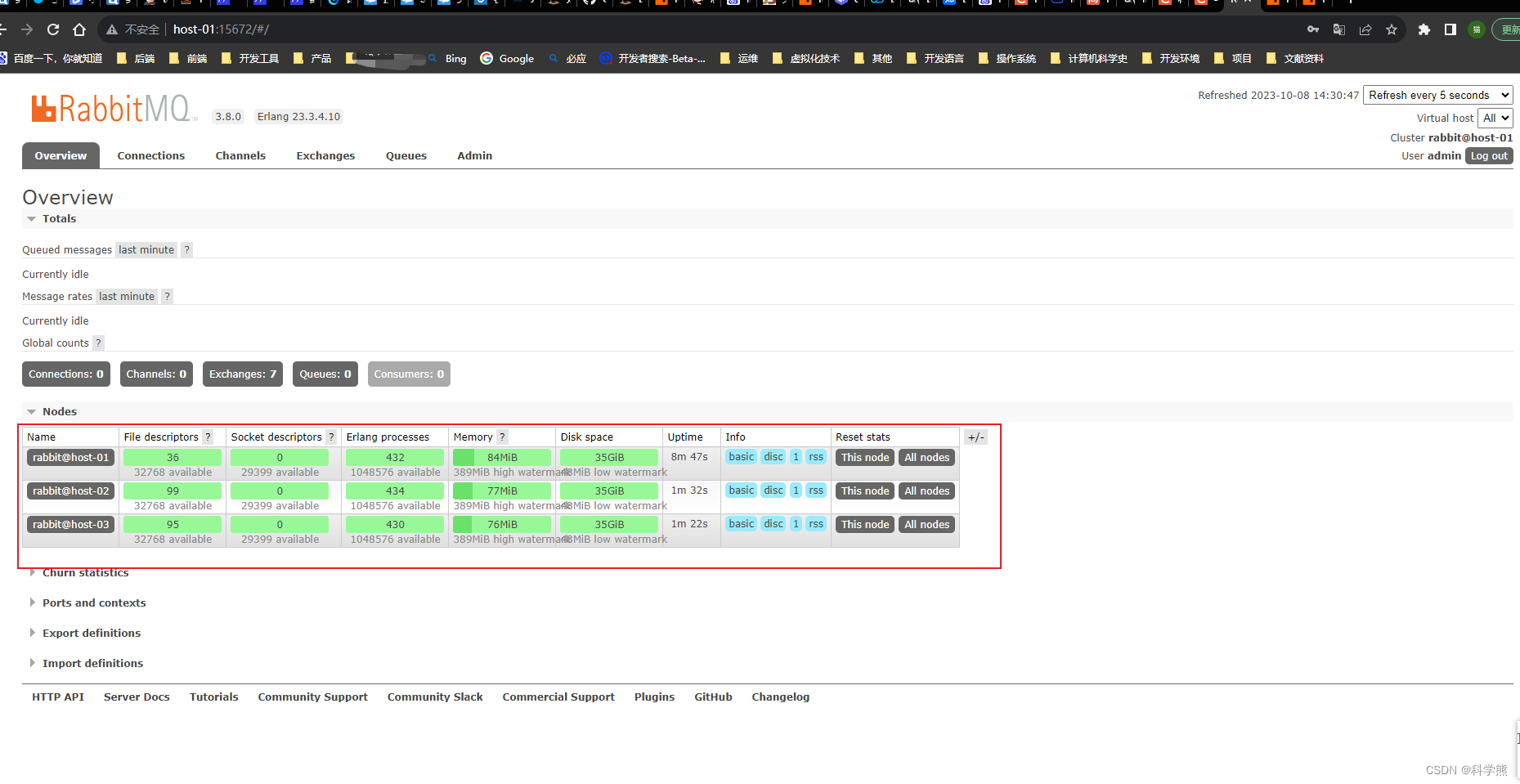
Linux虚拟机搭建RabbitMQ集群
普通集群模式,意思就是在多台机器上启动多个 RabbitMQ 实例,每台机器启动一个。创建的 queue,只会放在一个 RabbitMQ 实例上,但是每个实例都同步 queue 的元数据(元数据可以认为是 queue 的一些配置信息,通…...
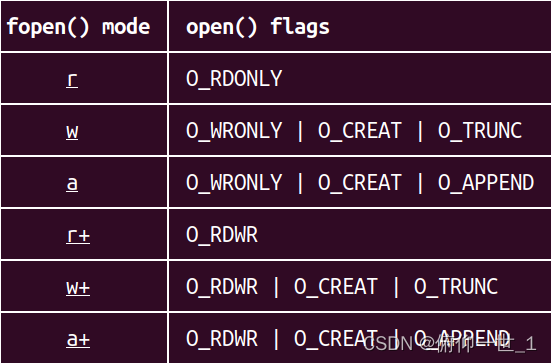
C之fopen/fclose/fread/fwrite/flseek
一、C中文件操作简介 c中的文件操作大致和linux的文件操作类似,但是毕竟是不同的API,所以会有些差异。部分差异会在下面的案例中体验 二、fopen open的参数有两个一个是文件名,一个是模式选择,不同open函数,open中的模…...

3D机器视觉:解锁未来的立体视野
原创 | 文 BFT机器人 机器视觉领域一直在不断演进,从最初的二维图像处理,逐渐扩展到了更复杂的三维领域,形成了3D机器视觉。3D机器视觉技术的涌现为计算机系统带来了全新的感知和理解能力,这一领域的发展正日益受到广泛关注。本文…...
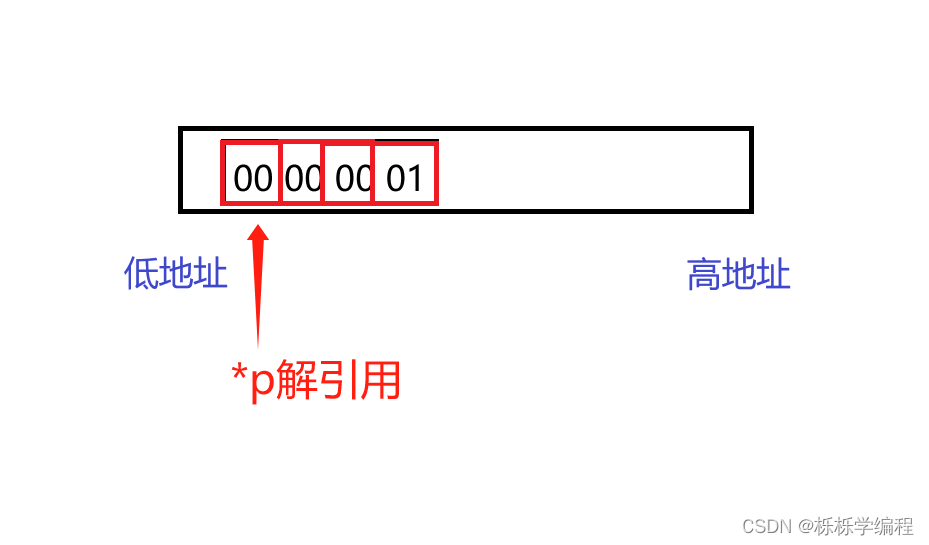
大端字节序存储 | 小端字节序存储介绍
为什么存储的顺序有些变动呢? 大小端的介绍 我们在创建变量时,操作系统就会给你分配空间,比如你创建了【short/int/double/float】的变量,这些变量的类型都是大于1个字节的,操作系统会根据你这个变量的类型ÿ…...
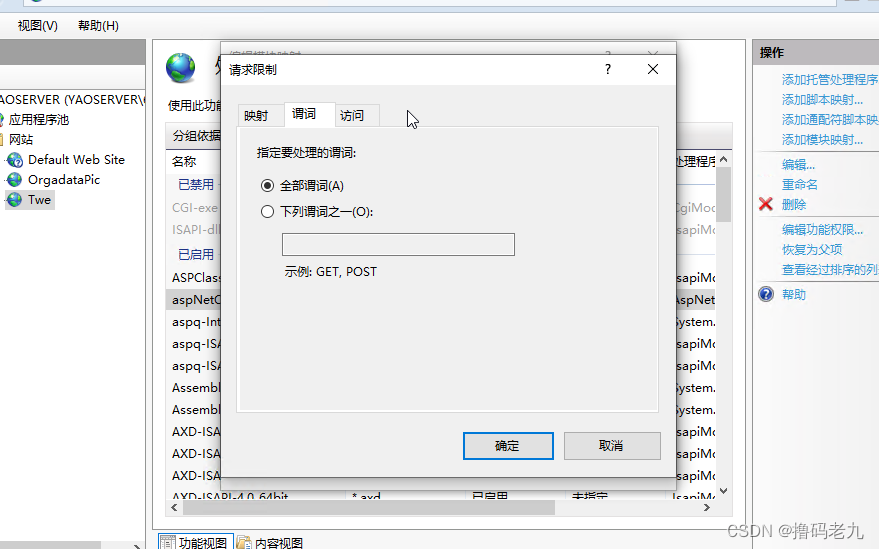
ASP.Core3.1 WebAPI 发布到IIS
本篇文章简述如何在IIS中发布你的.Core 程序 1.打包 首先你要打包好你程序,如果你是Visual Studio开发的程序,那你右击你的项目点击发布 如果你是Visual Code 开发的,那你在你的终端切换到你的目录然后执行命令 dotnet publish --config…...
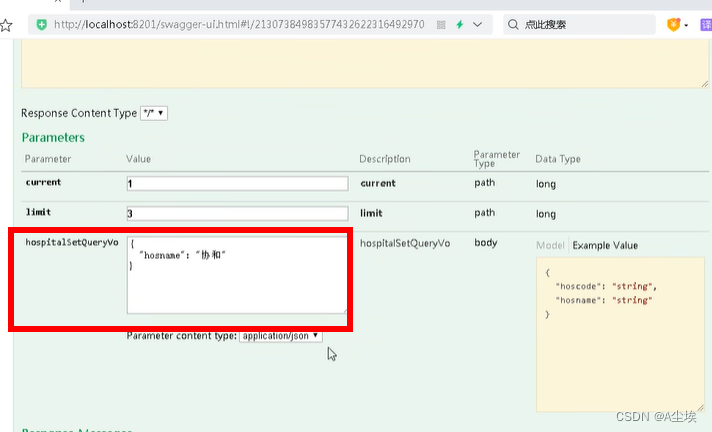
MyBatisPlus属性自动填充和乐观锁插件+查询删除操作+整合SpringBoot出现问题解决
属性字段自动填充 一、实体类和数据表添加两个字段(属性) 表:create_tiem/update_time 实体类:createTime/updateTime 二、实体类中属性进行注解添加 TableField(fillFieldFill.INSERT) private Date createTime;TableField(f…...

软件测试/测试开发丨App自动化—CSS 定位与原生定位
点此获取更多相关资料 本文为霍格沃兹测试开发学社学员学习笔记分享 原文链接:https://ceshiren.com/t/topic/27684 一、原生定位 元素属性定位组合定位 # ID 定位 driver.find_element_by_android_uiautomator(\new UiSelector().resourceId("<element-I…...
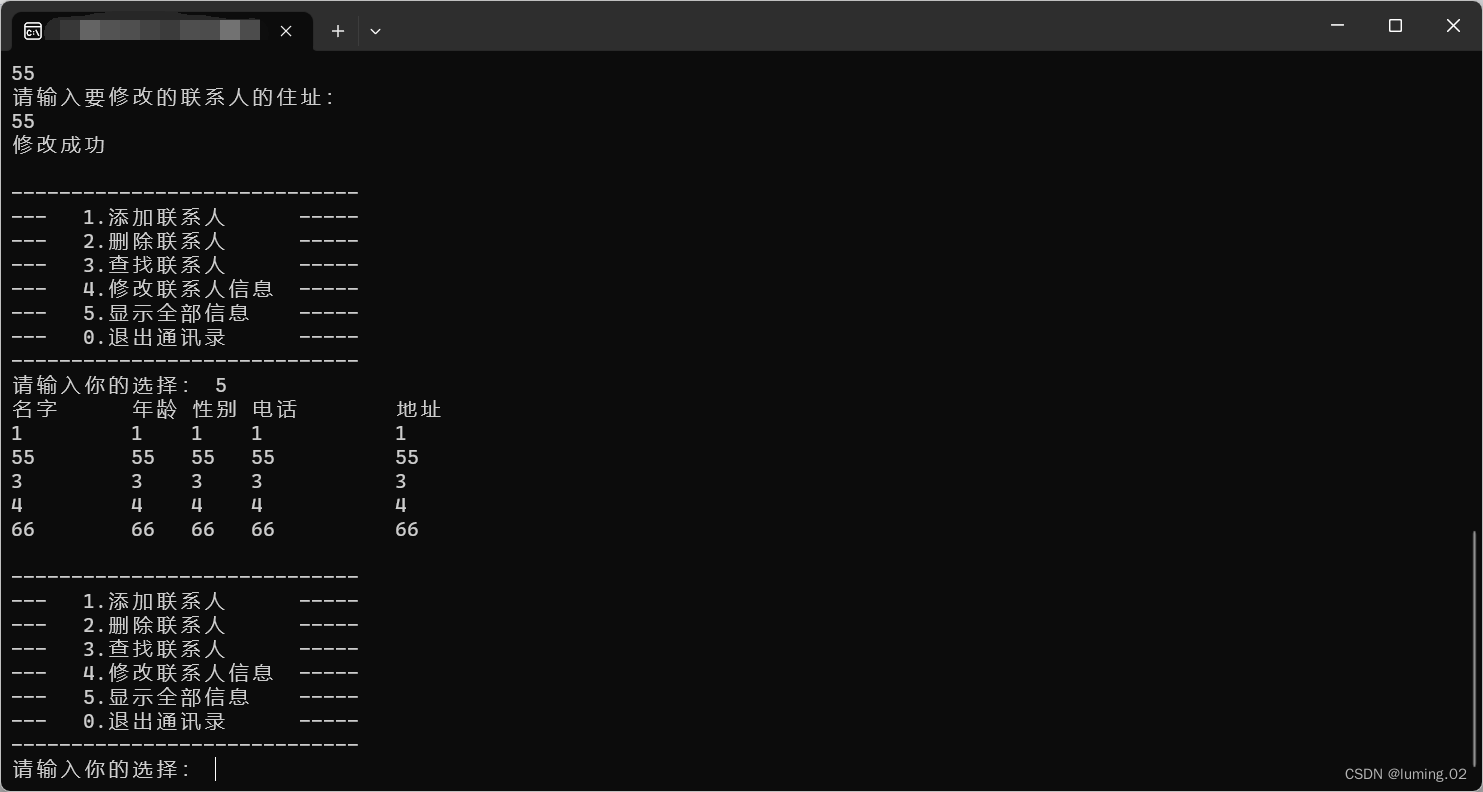
c语言:通讯录管理系统(文件版本)
前言:在大多数高校内,都是通过设计一个通讯录管理系统来作为c语言课程设计,通过一个具体的系统设计将我们学习过的结构体和函数等知识糅合起来,可以很好的锻炼学生的编程思维,本文旨在为通讯录管理系统的设计提供思路和…...

Android Studio 配置Git SVN忽略文件
在使用Android Studio进行版本控制时,经常会遇到需要忽略某些文件的情况,比如临时文件、编译生成的文件等。这些文件虽然在项目中存在,但不希望被加入到版本控制中。 在Android Studio中设置忽略文件 在Android Studio中,我们可…...

独享IP地址的层级划分和管理:打造稳定高效的网络架构
在网络架构设计中,独享地址的层级划分和管理是一项关键任务。它不仅能提供更好的网络性能和安全性,还能帮助企业实现更高效的资源管理。本文将为您详细介绍独享地址的层级划分和管理的重要性,并提供具体的方案和实际操作建议。 第一部分&…...

js中async的作用
async是JavaScript中的关键字,用于表示函数是异步的。 当函数被标记为async时,该函数会自动返回一个Promise对象,这个Promise对象的状态可能为resolved或rejected,具体取决于函数内部的操作和返回值。 使用async关键字时&#x…...

什么是信创测试?信创测试工具有哪些?
信创全称是“信息技术应用创新”,旨在实现信息技术自主可控,规避外部技术制裁和风险,其涉及产业链包括硬件、基础软件、应用软件、云服务、数据安全等领域。 信创测试是指对信创工程项目中的产品、系统等进行测试和验证,以确保其…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

